logo资料库

光学成像公式及摄像物镜知识介绍.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.61M 资料格式：pdf 举报 版权申诉
第1页 / 共35页
第2页 / 共35页
第3页 / 共35页
第4页 / 共35页
第5页 / 共35页
第6页 / 共35页
第7页 / 共35页
第8页 / 共35页
资料共35页，剩余部分请下载后查看
    1．光学基础 本章将介绍光学系统的成像公式和光学系统的基本形式、辐射度量的定义和单位、光学度量 的定义和单位、色度量的述语、国际标准（CIE）色度系统和光源系统。以上为设计机器视 觉系统建立基础。 1.1.1 光学成像公式 理想光学系统的成像公式 （1）成像的几何关系 1.1 光学系统 见图 1.1－1，图中也给出了各符号的定义。 图 1.1－1 理想光学系统的成像 （2）物像公式 1 l ' =+ 1 l 1 f （3）物距 l = b B ⎛ ⎜ ⎝ + ⎞ 1 ⎟ ⎠ f 式中 B 为物面宽度，b 为像面上探测器宽度。
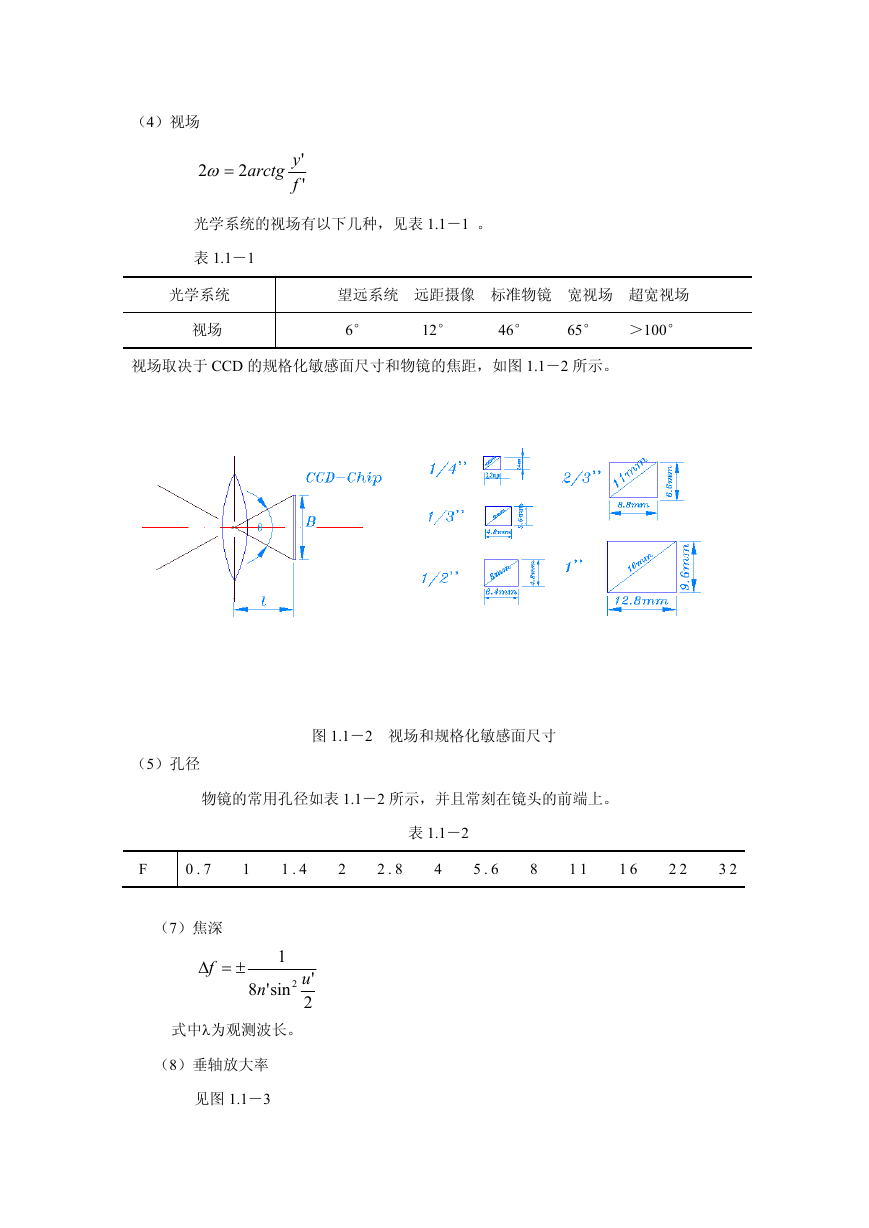
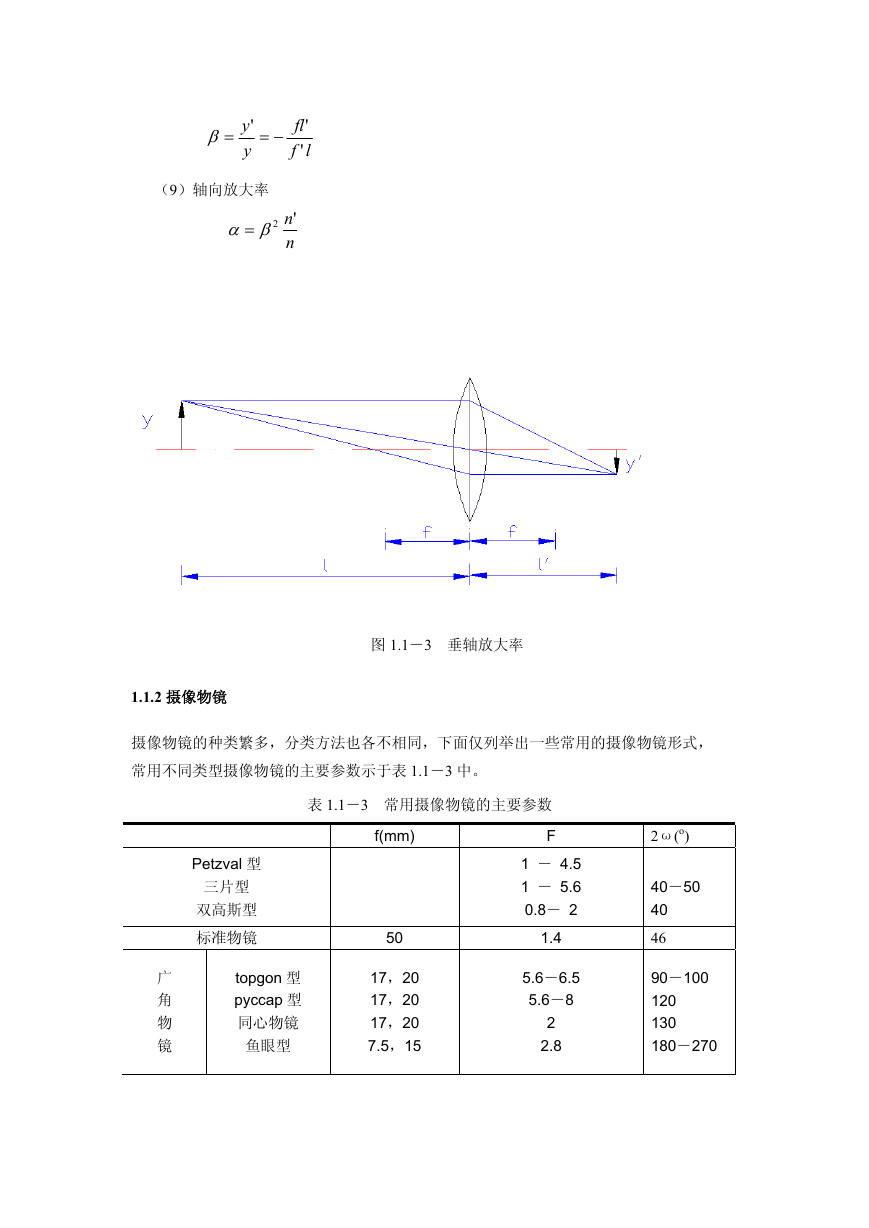
    （4）视场 2 =ω 2 arctg y f ' ' 光学系统的视场有以下几种，见表 1.1－1 。 表 1.1－1 光学系统 视场 望远系统 远距摄像 标准物镜 宽视场 超宽视场 6° 12° 46° 65° ＞100° 视场取决于 CCD 的规格化敏感面尺寸和物镜的焦距，如图 1.1－2 所示。 图 1.1－2 视场和规格化敏感面尺寸 （5）孔径 物镜的常用孔径如表 1.1－2 所示，并且常刻在镜头的前端上。 表 1.1－2 F 0 . 7 1 1 . 4 2 2 . 8 4 5 . 6 8 1 1 1 6 2 2 3 2 （7）焦深 f ±=Δ 1 n sin'8 2 u ' 2 式中λ为观测波长。 （8）垂轴放大率 见图 1.1－3
    =β y ' y −= fl ' lf ' （9）轴向放大率 2βα= n' n 图 1.1－3 垂轴放大率 1.1.2 摄像物镜 摄像物镜的种类繁多，分类方法也各不相同，下面仅列举出一些常用的摄像物镜形式， 常用不同类型摄像物镜的主要参数示于表 1.1－3 中。 表 1.1－3 常用摄像物镜的主要参数 Petzval 型 三片型 双高斯型 标准物镜 广 角 物 镜 topgon 型 pyccap 型 同心物镜 鱼眼型 f(mm) 50 17，20 17，20 17，20 7.5，15 F 1 － 4.5 1 － 5.6 0.8－ 2 1.4 5.6－6.5 5.6－8 2 2.8 2ω(o) 40－50 40 46 90－100 120 130 180－270
    折反射型 缩微物镜 远摄物镜 远距物镜 反远距物镜 畸变物镜 变焦距物镜 28－50 0.75 25.0≥NA 4 2.8－4 2.5－4 22 3.5 15 12 60－90 >180 75－46 下面便按照表 1.1－8 的顺序介绍常用摄像物镜的基本型结构及其主要参数。在这些基本型 结构的基础上还出现了许多改进型。 1）Petzval 物镜 Petzval 物镜是由彼此分开的两个正光焦度透镜组所组成的，如图 1.1－4 所示。它的特 点是孔径大而视场小，例如，f´=100mm 时，F 数＝1.6，而 2w＝10° 2）三片型物镜 典型三片型物镜是柯克三片型物镜，它由三个单透镜“正、负、正”组成，见图 1.1－5， 它的视场比 petzval 型物镜的大，而相对孔径却要小些，例如， f´=75mm 时，2ω＝10°， F 数＝4.5. 图 1.1－4 petzval 物镜
    图 1.1－5 三片物镜 3）双高斯型物镜 大孔径摄像物镜（系指 F 数<2 ），经常采用双高斯型物镜及其改进物镜，其基本结构型 式如图 1.1－6 所示。这是一种用厚透镜来校正像面弯曲的系统。 当物体位于二倍焦距位置，光栏位于系统的中间，双高斯型物镜结构完全对称于光栏时，垂 轴像差可以自动消除。完全对称结构的双高斯型物镜，其半部由弯月形的厚透镜和一个单正 透镜所组成。厚透镜用于校正 SⅣ，单透镜的弯曲用于校正 SⅠ。两个半部之间的间距用于校 正 SⅡ。在厚镜中引入一个胶合面来校正色差（CⅠ）。这样，结构完全对称的一倍成像系统， 七种初级像差就得到校正了。 图 1.1－6 双高斯物镜 双高斯型物镜的主要缺点是轴外高级负球差和高级正像散较大。典型双高斯物镜例的参 数为：f´=50mm，F 数＝2，而 =ω2 50°。 4）广角物镜 广角物镜的视场超过 60°，而视场超过 100°的物镜则称为超广角物镜。
    广角物镜大都采用对称结构，光栏位于镜组中央，镜片相对光阑对称，如图 1.1－7 至 1.1 －12 所示。镜片相对光阑对称排列可以消除畸变，这对于扩大物镜视场是十分有利的。 最早出现的对称物镜是 Hypogon 物镜，见图 1.1－7，它仅由两片对称的正透镜组成，相对 孔径很小。 在 Hypogon 物镜的里面加入一组对称于光阑的负透镜就得到如图 1.1－8 所示的 Topogon 物 镜，它的相对孔径为 1：6.3，视场角为 100°，畸变为 0.3％。 另一类对称型广角和超广角物镜是著名的 Pyccap 物镜，它的半部可以看作是 Hill 全 天物镜，如图 1.1－9 所示。而 Hill 物镜则可看作是鱼眼物镜的雏型。Pyccap 物镜是把 Hill 物镜对称于光阑重叠起来，如图 1.1－10 所示。它的相对孔径为 1：8，视场角为 122°，而 畸变显著减小到 0.07％，是用于航空摄像测量最优良的物镜。 图 1.1－7 Hypogon 物镜 图 1.1-8 Topgon 物镜
    图 1.1－9 Hill 全天物镜 图 1.1－10 Pyccap 物镜 同心物镜指所有球面具有同一个曲率中心的物镜。这种物镜成像在凹球面上。这个凹球面的 表面曲率中心就是入射光瞳和出射光瞳，因而也就是孔径光阑的中心。主光线无折射地通过， 并且具有光线沿光轴通过的性质。轴上光束和倾斜光束也是相同的（图 1.1－11 所示）因此 像差校正归结为球差校正。彗差、像散和畸变在同心物镜中是没有的。 同心物镜的特点是广角（2ω≈130°）和很大的相对孔径（～1：2）。 很多广角和超广角物镜，乃至鱼眼物镜，都是对前组进行复杂而获得的。图 1.1－12 所示的鱼眼物镜，它的相对孔径为 1：2.8，视场角为 180°，而畸变为 100％。 有的鱼眼物镜的视场角更大，甚至高达 270°。
    图 1.1－11 同心物镜 图 1.1－12 鱼眼物镜 5）折反射型物镜 当焦距很长时，折反射型物镜与折射式物镜相比，像差容易校正，尤其是二级光谱可 以消除。而且因光路折叠，可以得到特别紧凑的结构。 简单的折反射型物镜，采用球面或非球面的校正板来校正反射镜的球差。图 1.1－13 所示的结构型式称为 Schmidt 系统，前面是一块非球面校正板，称为 Schmidt 校正板，它的 相对孔径可达 1：0.75，视场角为 15°。图 1.1－14 所示的结构型式称为 MadcyTOB 系统， 是 MadcyTOB 用弯月形透镜代替了 Schmidt 校正板。它的性能与 Schmidt 系统相似。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料