第1页 / 共634页
第2页 / 共634页
第3页 / 共634页
第4页 / 共634页
第5页 / 共634页
第6页 / 共634页
第7页 / 共634页
第8页 / 共634页
[高清晰版奥本海默信号与系统第二版课后习题解答].solutions.manual.signals.and.systems.(2....pdf
CHAPTER 1
1.1 to 1.41 - part of text
1.42
(a) Periodic:
Fundamental period = 0.5s
(b) Nonperiodic
(c) Periodic
Fundamental period = 3s
(d) Periodic
Fundamental period = 2 samples
(e) Nonperiodic
(f) Periodic:
Fundamental period = 10 samples
(g) Nonperiodic
(h) Nonperiodic
(i) Periodic:
Fundamental period = 1 sample
l.43
y t( )
=
3
cos
200t
2
---+
6
2
=
9
cos
200t
---+
6
=
9
---
2
cos
400t
1
---+
3
(a) DC component =
9
---
2
(b) Sinusoidal component =
9
---
2
cos
400t
---+
3
Amplitude =
9
---
2
1
p
Ł
ł
Ł
ł
p
Ł
ł
p
Ł
ł
p
Ł
ł
Fundamental frequency =
200
p---------Hz
1.44
The RMS value of sinusoidal x(t) is
A
2⁄
. Hence, the average power of x(t) in a 1-ohm
resistor is
(
A
2⁄
)2
= A2/2.
1.45
Let N denote the fundamental period of x[N]. which is defined by
N
=
2p
W------
The average power of x[n] is therefore
N -1
x2 n[ ]
n=0
N -1
2
A2
cos
P
=
=
=
1
----
N
1
----
N
A2
------
N
2p n
----------
N
f+
n=0
N -1
n=0
2
cos
2p n
----------
N
f+
1.46
The energy of the raised cosine pulse is
E
w ⁄
w ⁄–
w ⁄
=
=
1
---
2
=
1
---
2
0
--- 3
1
---Ł
2
2
=
0
w ⁄
1
---
4
(
(
(
cos
)
t
1+
)2 td
2
(
cos
)
t
+
2
cos
(
)
t
1+
) td
cos
(
2w
)
t
+ +
1
---
2
2
cos
(
)
t
1+
td
3p
=
⁄
4w
1
---
2
w----
1.47
The signal x(t) is even; its total energy is therefore
E
5=
2
0
x2 t( ) td
2
Ł
ł
Ł
ł
w
p
p
w
w
p
w
Ł
ł
p
ł
p
Ł
ł
4=
2
1( )2 t
0
2 t[ ]
=
4
t=0
+
t–(
5
5+d
2
4
1
t–(
--- 5
3
2
–
)2 td
5
)3
t=4
=
8
2
---+
3
=
26
------
3
1.48
(a) The differentiator output is
y t( )
=
1
1–
0
4–
< <
5
for
–
t
< <
for 4
5
t
otherwise
(b) The energy of y(t) is
5+d
2
4–=
5–
=
1+
1
1( )2 t
E
=
4
1–(
)2 td
1.49
The output of the integrator is
y t( )
for
At
td
=
=
t
A t
0
Hence the energy of y(t) is
E
=
T
0
A2t2 td
=
A2T 3
-------------
3
0
t T
x(5t)
1.0
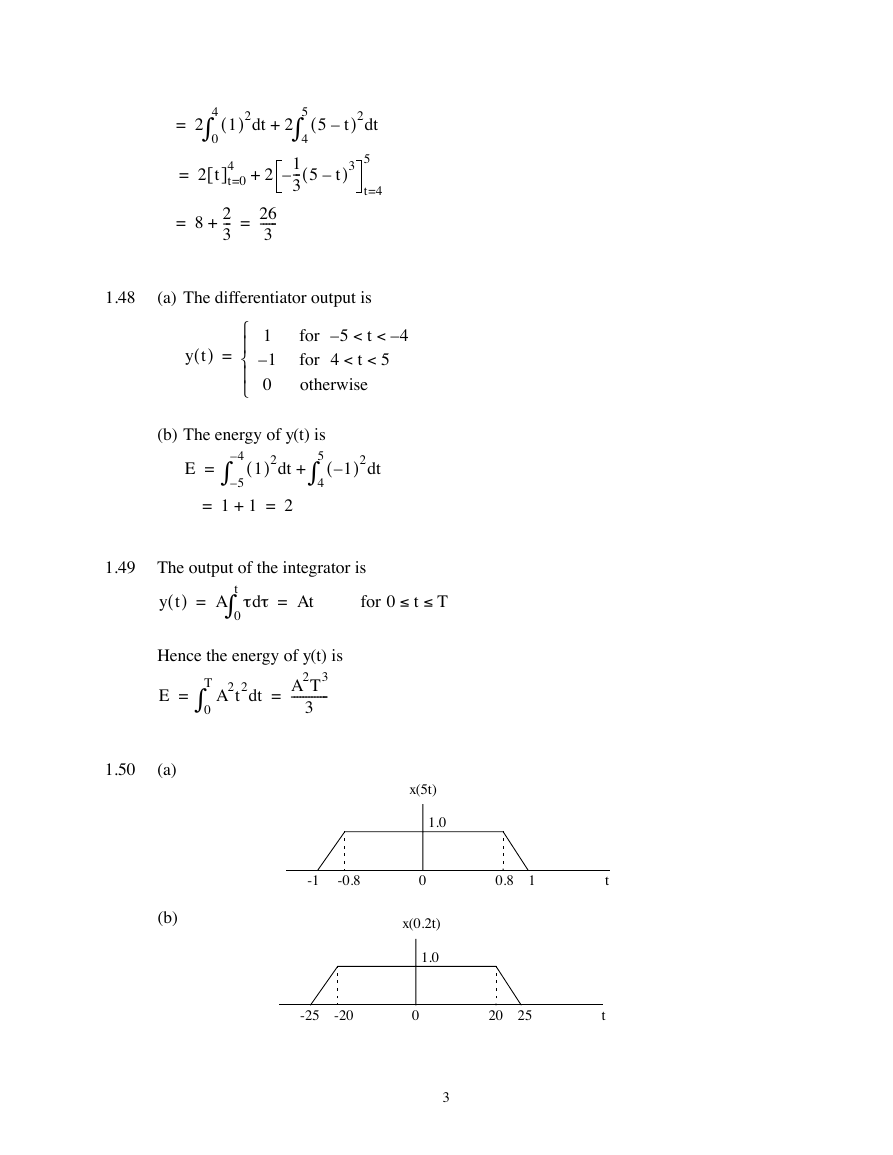
1.50
(a)
(b)
-1 -0.8 0 0.8 1
x(0.2t)
1.0
-25 -20 0 20 25
t
t
3
£
£
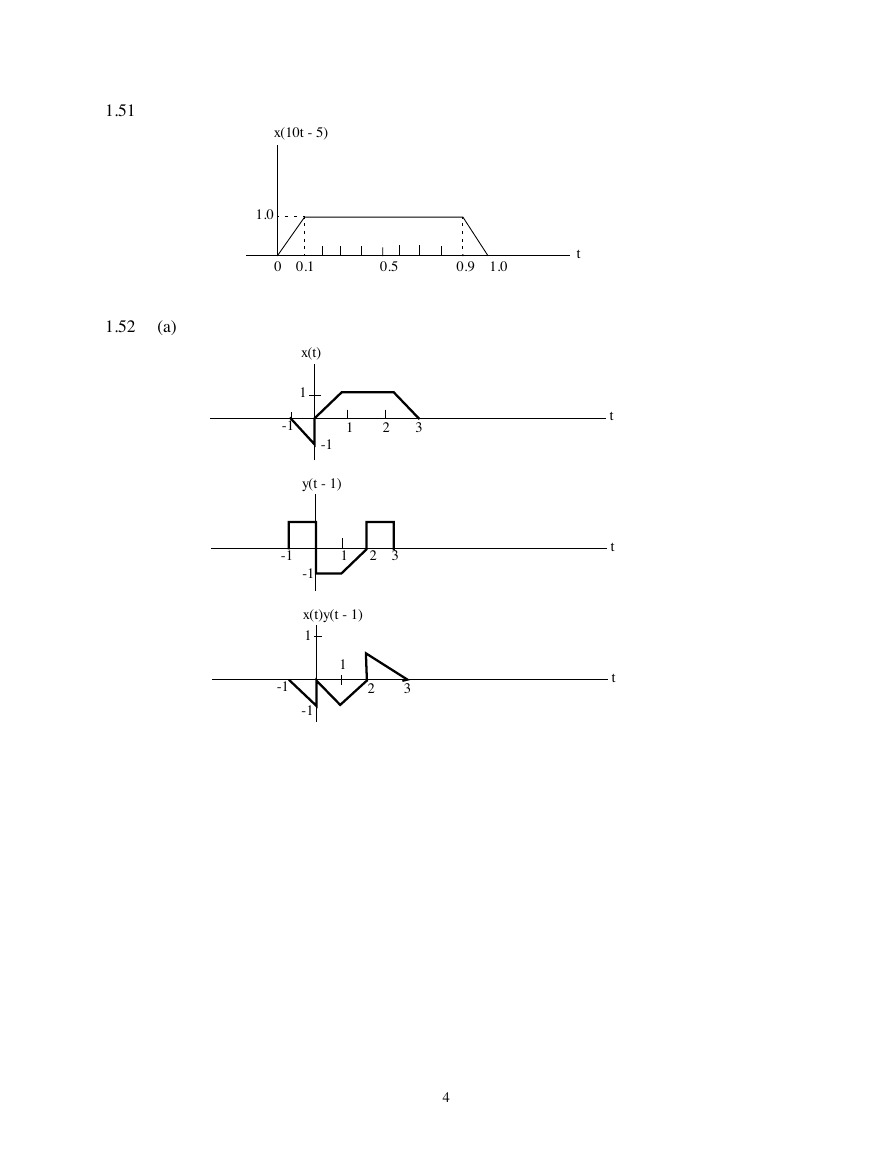
1.51
1.52
(a)
x(10t - 5)
1.0
0 0.1 0.5 0.9 1.0
t
x(t)
1
-1
1 2 3
-1
y(t - 1)
-1 1 2 3
-1
x(t)y(t - 1)
1
1
-1
-1
2 3
t
t
t
4
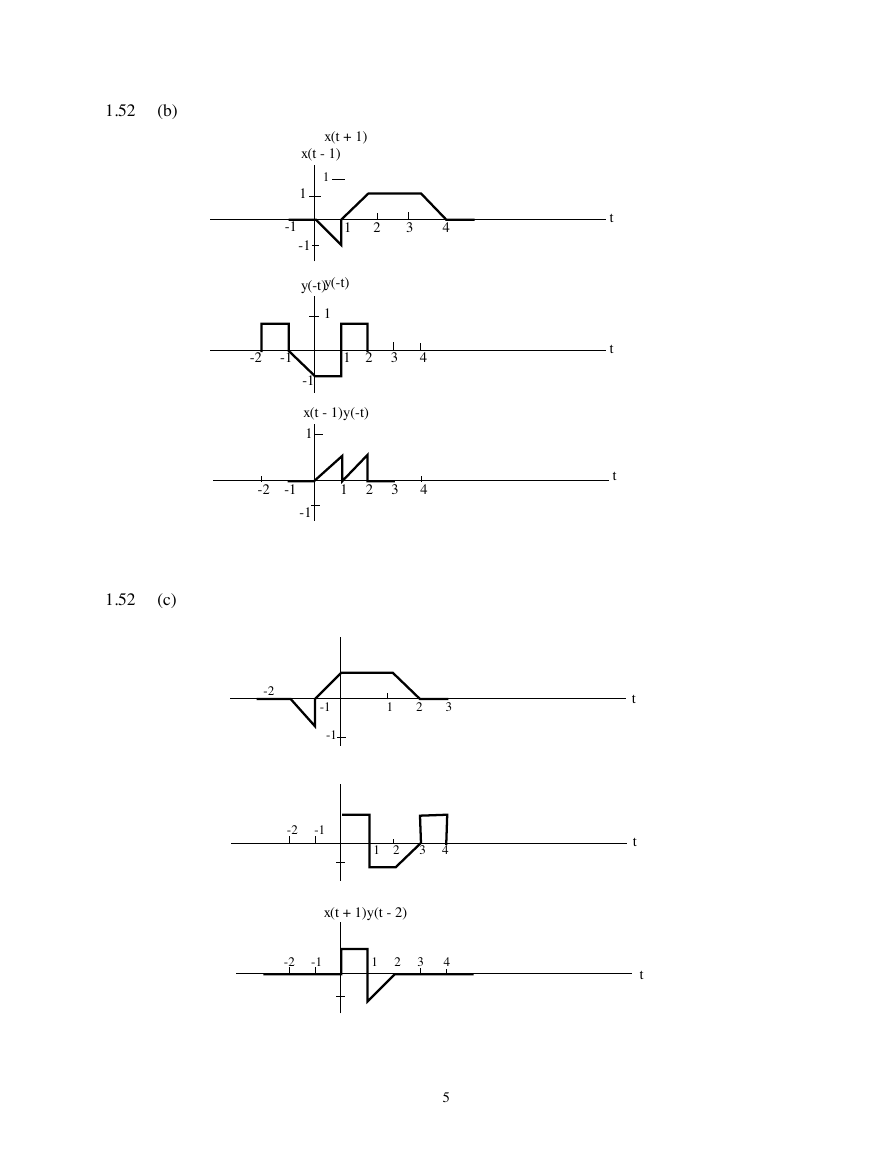
1.52
(b)
1.52
(c)
x(t + 1)
x(t - 1)
1
1
-1
-1
1 2 3 4
y(-t)
y(-t)
1
-2 -1 1 2 3 4
-1
x(t - 1)y(-t)
1
-2 -1 1 2 3 4
-1
-2
-1 1 2 3
-1
-2 -1
1 2 3 4
x(t + 1)y(t - 2)
-2 -1 1 2 3 4
5
t
t
t
t
t
t
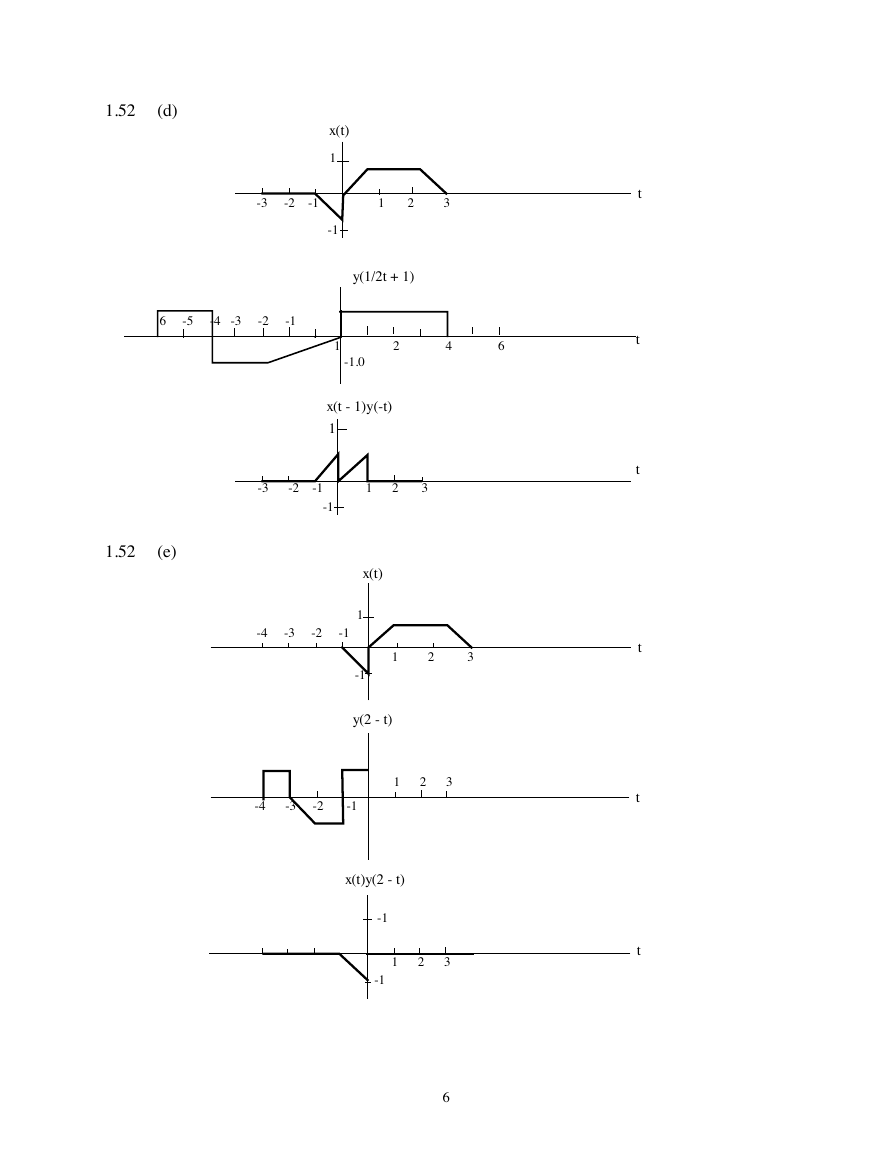
1.52
(d)
x(t)
1
-3 -2 -1 1 2 3
-1
y(1/2t + 1)
6 -5 -4 -3 -2 -1
1 2 4 6
1.52
(e)
-1.0
x(t - 1)y(-t)
1
-3 -2 -1 1 2 3
-1
-4 -3 -2 -1
x(t)
1
-1
1 2 3
y(2 - t)
1 2 3
-4 -3 -2 -1
x(t)y(2 - t)
-1
-1
1 2 3
6
t
t
t
t
t
t
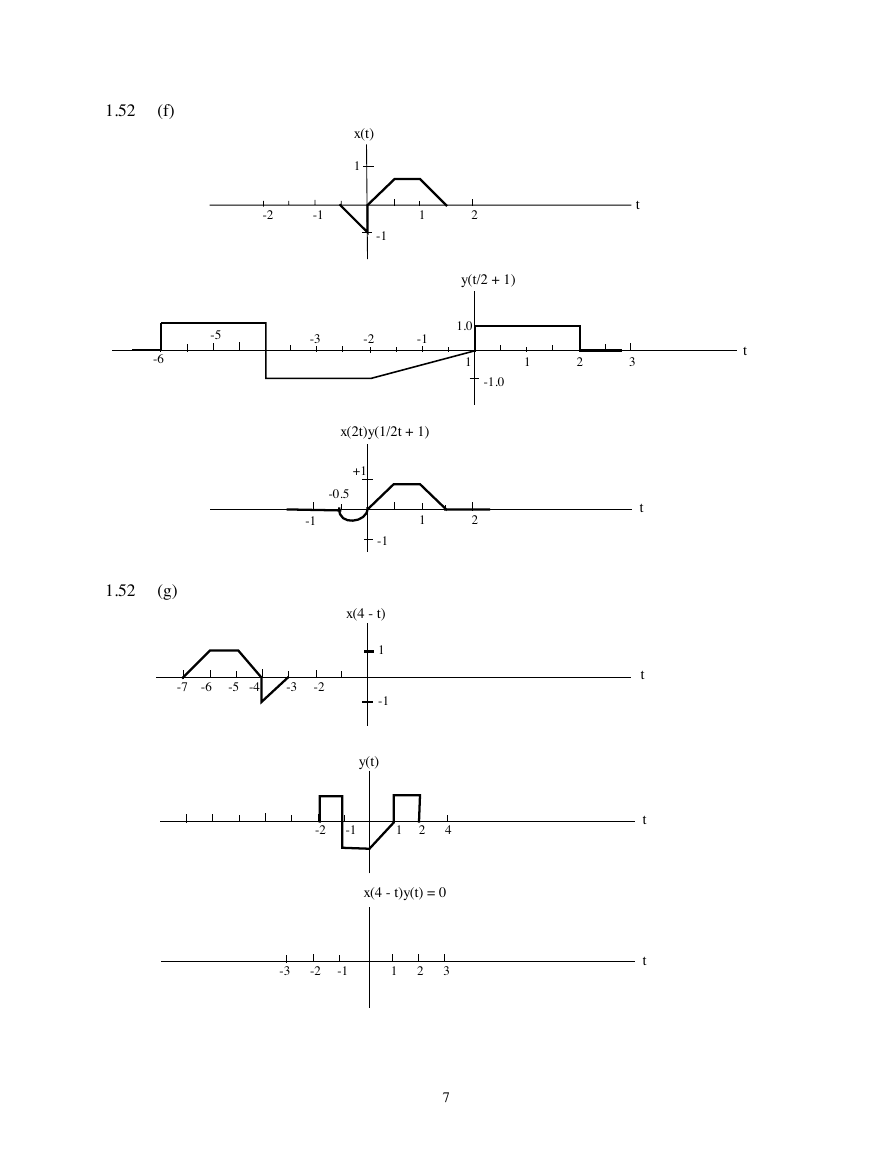
1.52
(f)
x(t)
1
-2 -1 1 2
-1
-5
-3 -2 -1
y(t/2 + 1)
1.0
-6
1 1 2 3
-1.0
x(2t)y(1/2t + 1)
+1
-0.5
-1
1 2
1.52
(g)
-7 -6 -5 -4 -3 -2
-1
x(4 - t)
1
-1
y(t)
-2 -1 1 2 4
x(4 - t)y(t) = 0
-3 -2 -1 1 2 3
7
t
t
t
t
t
t
1.53 We may represent x(t) as the superposition of 4 rectangular pulses as follows:
g1(t)
1
1 2 3 4
g2(t)
1
g3(t)
1
g4(t)
11 2 3 4
1 2 3 4
1
0
1 2 3 4
t
t
t
t
)
=
b–
(
g at
To generate g1(t) from the prescribed g(t), we let
g1 t( )
where a and b are to be determined. The width of pulse g(t) is 2, whereas the width of
pulse g1(t) is 4. We therefore need to expand g(t) by a factor of 2, which, in turn, requires
that we choose
a
1
---=
2
The mid-point of g(t) is at t = 0, whereas the mid-point of g1(t) is at t = 2. Hence, we must
choose b to satisfy the condition
a 2( )
or
0=
b–
b
=
2a
=
2
1
---Ł
2
=
1
Hence,
g1 t( )
=
g
1
---t
2
1–
g
=
Proceeding in a similar manner, we find that
g2 t( )
g3 t( )
g4 t( )
Accordingly, we may express the staircase signal x(t) in terms of the rectangular pulse g(t)
as follows:
2
5
---t
---–
3
3
3–(
)
g t
(
g 2t
7–
=
=
)
8
ł
Ł
ł
Ł
ł
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
