第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
f（R）重力下的准宇宙学遍历虫洞.pdf
Quasi-cosmological traversable wormholes in f(R) gravity
Abstract
1 Introduction
2 f(R) gravity wormholes
3 Traversable wormhole solutions in f(R) models
3.1 The case of c1=0
3.2 The cases of c1neq0
4 Conclusion
Acknowledgements
References
Eur. Phys. J. C (2019) 79:777
https://doi.org/10.1140/epjc/s10052-019-7292-4
Regular Article - Theoretical Physics
Quasi-cosmological traversable wormholes in f (R) gravity
Hanif Golchina, Mohammad Reza Mehdizadehb
Faculty of Physics, Shahid Bahonar University of Kerman, PO Box 76175, Kerman, Iran
Received: 6 March 2019 / Accepted: 9 September 2019 / Published online: 20 September 2019
© The Author(s) 2019
Abstract
In this paper, we study traversable wormholes in
the context of f (R) gravity. Exact solutions of traversable
wormholes are found by imposing the nonconstant Ricci
scalar. These solutions asymptotically match spherical, flat
and hyperbolic FRW metric. By choosing some static f (R)
gravity models, we verify the standard energy conditions for
the asymptotically spherical, flat and hyperbolic wormhole
solutions. Unlike the Einstein gravity, we find that in the con-
text of f (R) modified gravity, the asymptotically spherical,
flat and hyperbolic wormhole solutions can respect the null
energy condition (NEC) at the wormhole throat and near that.
We find that in some static f (R) models, asymptotically flat
and hyperbolic wormholes respect the weak energy condition
(WEC) through the whole space.
1 Introduction
Traversable wormholes are throatlike geometrical structures
which connect two separate and distinct regions of space-
times and have no horizon or singularity. There are some
hints in the paper of Flamm [1], to such spatial geometry.
In 1935, Einstein and Rosen [2] firstly obtained the worm-
hole solutions as bridge model of a particle . The study of
Lorentzian wormholes in the context of general relativity
(GR) was stimulated by the significant paper of Morris and
Thorne in 1988 [3,4]. A fundamental ingredient in worm-
hole physics is the flaring-out condition of the throat, which
in GR entails the violation of the NEC. Matter that violates
the NEC is denoted exotic matter.
A very important challenge in wormhole scenarios is the
establishment of standard energy conditions. In this regard,
various methods have been proposed in the literature that deal
with the issue of energy conditions within wormhole settings.
Work along this line has been done in dynamical wormholes
a e-mail: h.golchin@uk.ac.ir
b e-mail: mehdizadeh.mr@uk.ac.ir
[5–7] and thin-shell wormholes [8], where the supporting
matter is concentrated on the wormholes throat. In the con-
text of modified theories of gravity, the presence of higher-
order terms in curvature would allow for building thin-shell
wormholes supported by ordinary matter [9–11]. Recently,
many people try to build and study wormhole solutions within
the framework of modified gravity for instance, wormhole
solutions in BransDicke theory [12–15], Born–Infeld theory
[16,17], Einstein–Gauss–Bonnet theory [18,19], Kaluza–
Klein gravity [20,21] and scalar–tensor gravity [22] and
Einstein–Cartan theory [23–25].
In recent years, theories of modified gravity have been
studied involving cosmological objects like black holes,
gravastars, strange stars and wormholes. Such theories are
able to explain accelerating expansion of the universe and
also solve the dark matter problem [26–28]. A well-known
theory of modified gravity is f(R) gravity which modifies
GR by replacing the gravitational action R by an arbitary
function f(R), where R is the Ricci scalar. These models
can be demonstrated to cause acceleration [29–35]. It was
found that higher-order curvature invariants can satisfy the
energy conditions in f(R) gravity [36–38]. The power-law
Rm gravity is also studied in [39,40], the new static worm-
holes in f(R) theory using the non-commutative geometry are
built in [41,42] and the cosmological evolution of wormhole
solutions is investigated in [43,44]. Recently, the junction
conditions in f(R) applied to the construction of thin-shell
wormholes [45–47] and pure double layer bubbles [48]. The
static wormhole geometries have also been theorized within
curvature-matter coupling theories such as f(R, T) [49,50].
Lorentzian wormhole solutions were also investigated in
viable f(R) modified theories of gravity [51], which are con-
sistent with observations of the solar system and cosmolog-
ical evolution in [52–57]. These wormholes were found in
specific f(R) models which are considered to reproduce real-
istic scenarios of cosmological evolution based on the accel-
erated expansion of the universe. it was shown that the WEC
holds at the vicinity of the throat for certain ranges of the free
123
777 Page 2 of 13
Eur. Phys. J. C (2019) 79 :777
parameters of the theory. These asymptotically flat solutions
analysed with the simple choices of shape function which
WEC is satisfied at a specific point in space.
A large class of static black hole solutions with non con-
stant Ricci scalar and traversable wormholes with constant
Ricci scalar have also investigated in the background of
f (R) gravity [58,59]. The existence of wormhole solutions
in scalar–tensor and f (R) gravity was studied in [60,61] and
it was shown that static wormhole solutions in these theories
can be obtained with matter respecting the WEC when the
effective gravitational constant is negative (which means the
anti-gravitational property of the solutions) in some regions
of space.
In this work, our aim is to obtain the wormhole solutions
with non constant Ricci scalar in the context of viable f(R)
gravity. This paper is organized as follows: after this intro-
duction, we will present the basic field equations of f(R) grav-
ity . In Sec. III, we will derive the properties of wormholes
solutions within the framework of f(R) gravity and discuss
about the energy conditions. The final section is devoted to
our concluding remarks.
2 f(R) gravity wormholes
(2)
d4x
d4x
√−g f (R) +
f gμν − ∇μ∇ν F + gμνF = T m
μν ,
The action of f(R) modified theories of gravity is given by
√−g Lm (gμν , ψ ) , (1)
S = 1
2κ
where κ = 8π G and Lm is the matter Lagrangian density, in
which the matter field ψ is minimally coupled to the metric
gμν. Throughout this work for notational simplicity we con-
sider κ = 1. One can find the field equation by varying the
action (1) with respect to metric gμν as
F Rμν − 1
2
and the trace of the field equation
F R − 2 f + 3 F = T ,
(3)
where F = d f /d R. Substituting the trace equation in (2)
and re-organizing the terms, one can write the field equation
as [62]
Gμν ≡ Rμν − 1
2
In the above, the two terms in the right hand side of the field
equation are in the form
∇μ∇ν F − 1
μν = 1
T c
4
F
˜T m
μν = T m
μν /F .
In this background, we are going to study the static and spher-
ically symmetric traversable wormholes which is given by the
gμν (R F + F + T )
R gμν = T c
μν + ˜T m
μν .
(4)
(5)
,
123
following metric1
ds2 = −dt 2 +
dr 2
1 − b(r )/r
+ r 2 (dθ 2 + sin2 θ dφ2) .
(6)
(7)
The Ricci scalar for the above wormhole geometry is
(r )
R = 2 b
r 2
,
” denotes derivative with respect to the radial coor-
where “
dinate r. As in [62] we choose the energy–momentum tensor
of anisotropic distribution of matter
Tμν = (ρ + pt )Uμ Uν + pt gμν + ( pr − pt ) χμχν ,
where U μ is the four-velocity and χ μ = √
(8)
1 − b(r )/r δμ
r
is the unit spacelike vector in the radial direction. ρ(r ) is
the energy density and pr (r ), pt (r ) are radial and transverse
pressure respectively, so the energy–momentum tensor takes
ν = diag[−ρ, pr , pt , pt] . Thus the field equa-
to the form T μ
tion (4) leads to the following relationships
,
,
,
b
F
r
F
− H
r − b
2r 2(1 − b/r )
− F
− H
= ρ
F
= pr
F
= pt
F
1− b
r
1 − b
(9)
r
(F R + F + T ). By solving the above
+ H
b
r 2
F
+ 1
− b
r 3
F
b−b
+ 1
r
2r 3
F
where H (r ) = 1
system, one finds the following expressions [62]
ρ = Fb
r 2
+ F
pr = − bF
r 3
2r 2
1 − b
pt = − F
r
r
r − b) − F
+ F
(b − b
2r 3
1 − b
r
(10)
(11)
(12)
r ) .
(b
4
,
,
We are interested in studying inhomogeneous spacetimes
which merge smoothly to the cosmological background.
Therefore, we may consider the Ricci scalar of the worm-
hole geometry as
R = 6 c1 + 6 c2
r n
where c1, c2 and n are free parameters. In the following sec-
tion we consider some choices for these free parameters and
study the corresponding wormhole solutions in some differ-
ent f (R) backgrounds.
(13)
,
1 The static and spherically symmetric wormhole geometry is given by
ds2 = −e2(r )dt 2 +
+ r 2 (dθ 2 + sin2 θ dφ2) .
dr 2
1 − b(r )/r
The solution is traversable when (r ) is finite. In the following we set
(r ) = 0.
Eur. Phys. J. C (2019) 79 :777
Page 3 of 13 777
(a)
(b)
(c)
Fig. 1 a–c Show the asymptotically flat (c1 = 0), asymptotically hyperbolic (c1 = −1) and asymptotically spherical (c1 = 1) wormhole solutions
respectively. Wormhole throat is chosen at r0 = 1, we also set n = 4 in these figures
3 Traversable wormhole solutions in f (R) models
We start this section by finding wormhole solutions with
Ricci scalar in the form (13). Combining (7) and (13) one
can find the shape function as
b(r ) = r 3
c1 + 3 c2
3 − n
+ c3,
(14)
−n
r
where c3 is the integration constant. This wormhole solution
by choosing c2 = 0 is obtained in [59]. In the following
we set the integration constant to zero. The shape function
b(r ) for a wormhole solution, should satisfy the following
conditions:
i)
ii)
iii)
b(r0) = r0 ,
(r0) < 1 ,
b
1 − b(r )
r
> 0 .
(15)
Inserting condition i), one can find c2 in terms of r0, c1 and
n; so it is possible to rewrite the shape function as
b(r ) =
r 3−n + c1 r 3
0 c1 + r n−2
−r n
(16)
.
0
We consider the wormhole solutions with three values
c1 = 0,±1. The shape function for these values are depicted
in Fig. 1. It is easy to check that in the case of c1 = 0,−1
the condition ii) in (15) is satisfied for n > 2 and in the case
of c1 = 1 condition ii) is satisfied when n > 2.4 .
Setting the shape function into the form (16), one can write
b(r )
r
= c1 r 2 + (r n−2
0
− c1 r n
0
)r 2−n ,
(17)
note that due to the condition ii) we should insert n > 2 in
the above, so the second term in (17) falls down at large r.
Remembering the wormhole metric (6), one deduces that the
wormhole solutions with c1 = −1, c1 = 0 and c1 = 1 at
large r match the hyperbolic, flat and spherical FRW universe
respectively, so we call them asymptotically flat (c1 = 0),
asymptotically hyperbolic (c1 = −1) and asymptotically
spherical (c1 = 1) wormhole solutions.
)
−n(c1 r n
In the framework of Einstein gravity, the traversable
wormhole geometry (6), violates the weak energy condition
WEC1: ρ > 0 , WEC2: ρ + pt > 0 , WEC3: ρ + pr > 0
and the null energy condition WEC2: ρ + pt > 0 , WEC3:
ρ+ pr > 0 . Substituting ρ, pr and pt given in (10)–(12) and
the shape function (16), one can rewrite the requirements of
WEC as
3c1 + (n − 3)r
WEC1:
WEC2: 1
F
2r
+2F
c1r 2−1+(r n−2
WEC3: F
12c1 − (n − 2)
12c1r + (6c1r n
6c1r 2−1+(r n−2
24 c1r+(4−n)(r n−2
− 6c1r n
r n−2
− r n−2
−6 r n
0 c1)
where F = d f (R)/d R and “
respect to the radial coordinate r.
− r n−2
− 6c1r n
)r 2−n
> 0,
− 6c1r n
−n
) (n − 2) r 1−n
r 2−n > 0,
F > 0 ,
)r 1−n
” denotes derivative with
+ 1
2
+F
(18)
F
r
0
0
0
0
0
0
0
0
0
0
0
The conditions of stability and absence of ghosts are dis-
cussed in [60,61]. It is shown that in a scalar–tensor theory
of gravity formulated in the Jordan frame with Lagrangian
L = 1
2
f (φ)R + h(φ)gμν φ,μφ,ν − 2U (φ)
+ Lm ,
(19)
where f , h and U are arbitrary functions and Lm is the matter
Lagrangian, there is no static wormhole solution that satisfy
the null energy conditions when f (φ) > 0 and f (φ) h(φ)+
2 > 0. In the case of f (R) theories of modified gravity
h(φ) = 0 and f (φ) = F = d f (R)/d R [61], so the above
nonexistence theorem holds for
d f
dφ
3
2
123
777 Page 4 of 13
Eur. Phys. J. C (2019) 79 :777
(a)
(b)
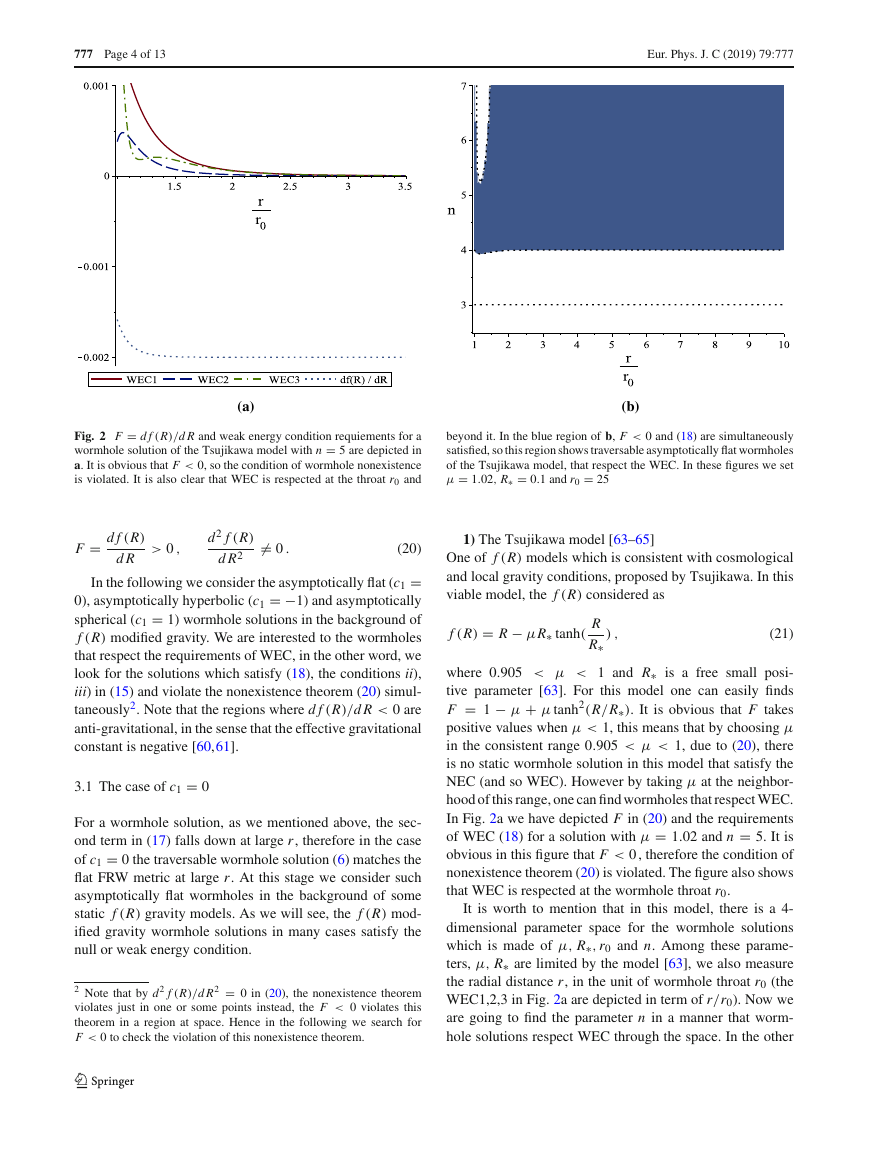
Fig. 2 F = d f (R)/d R and weak energy condition requiements for a
wormhole solution of the Tsujikawa model with n = 5 are depicted in
a. It is obvious that F < 0, so the condition of wormhole nonexistence
is violated. It is also clear that WEC is respected at the throat r0 and
beyond it. In the blue region of b, F < 0 and (18) are simultaneously
satisfied, so this region shows traversable asymptotically flat wormholes
of the Tsujikawa model, that respect the WEC. In these figures we set
μ = 1.02, R∗ = 0.1 and r0 = 25
> 0 ,
d R2
d2 f (R)
= 0 .
F = d f (R)
(20)
d R
In the following we consider the asymptotically flat (c1 =
0), asymptotically hyperbolic (c1 = −1) and asymptotically
spherical (c1 = 1) wormhole solutions in the background of
f (R) modified gravity. We are interested to the wormholes
that respect the requirements of WEC, in the other word, we
look for the solutions which satisfy (18), the conditions ii),
iii) in (15) and violate the nonexistence theorem (20) simul-
taneously2. Note that the regions where d f (R)/d R < 0 are
anti-gravitational, in the sense that the effective gravitational
constant is negative [60,61].
3.1 The case of c1 = 0
For a wormhole solution, as we mentioned above, the sec-
ond term in (17) falls down at large r, therefore in the case
of c1 = 0 the traversable wormhole solution (6) matches the
flat FRW metric at large r. At this stage we consider such
asymptotically flat wormholes in the background of some
static f (R) gravity models. As we will see, the f (R) mod-
ified gravity wormhole solutions in many cases satisfy the
null or weak energy condition.
2 Note that by d2 f (R)/d R2 = 0 in (20), the nonexistence theorem
violates just in one or some points instead, the F < 0 violates this
theorem in a region at space. Hence in the following we search for
F < 0 to check the violation of this nonexistence theorem.
123
1) The Tsujikawa model [63–65]
One of f (R) models which is consistent with cosmological
and local gravity conditions, proposed by Tsujikawa. In this
viable model, the f (R) considered as
f (R) = R − μR∗ tanh(
(21)
R
R∗ ) ,
where 0.905 < μ < 1 and R∗ is a free small posi-
tive parameter [63]. For this model one can easily finds
F = 1 − μ + μ tanh2(R/R∗). It is obvious that F takes
positive values when μ < 1, this means that by choosing μ
in the consistent range 0.905 < μ < 1, due to (20), there
is no static wormhole solution in this model that satisfy the
NEC (and so WEC). However by taking μ at the neighbor-
hood of this range, one can find wormholes that respect WEC.
In Fig. 2a we have depicted F in (20) and the requirements
of WEC (18) for a solution with μ = 1.02 and n = 5. It is
obvious in this figure that F < 0 , therefore the condition of
nonexistence theorem (20) is violated. The figure also shows
that WEC is respected at the wormhole throat r0.
It is worth to mention that in this model, there is a 4-
dimensional parameter space for the wormhole solutions
which is made of μ, R∗, r0 and n. Among these parame-
ters, μ, R∗ are limited by the model [63], we also measure
the radial distance r, in the unit of wormhole throat r0 (the
WEC1,2,3 in Fig. 2a are depicted in term of r/r0). Now we
are going to find the parameter n in a manner that worm-
hole solutions respect WEC through the space. In the other
Eur. Phys. J. C (2019) 79 :777
Page 5 of 13 777
(a)
(b)
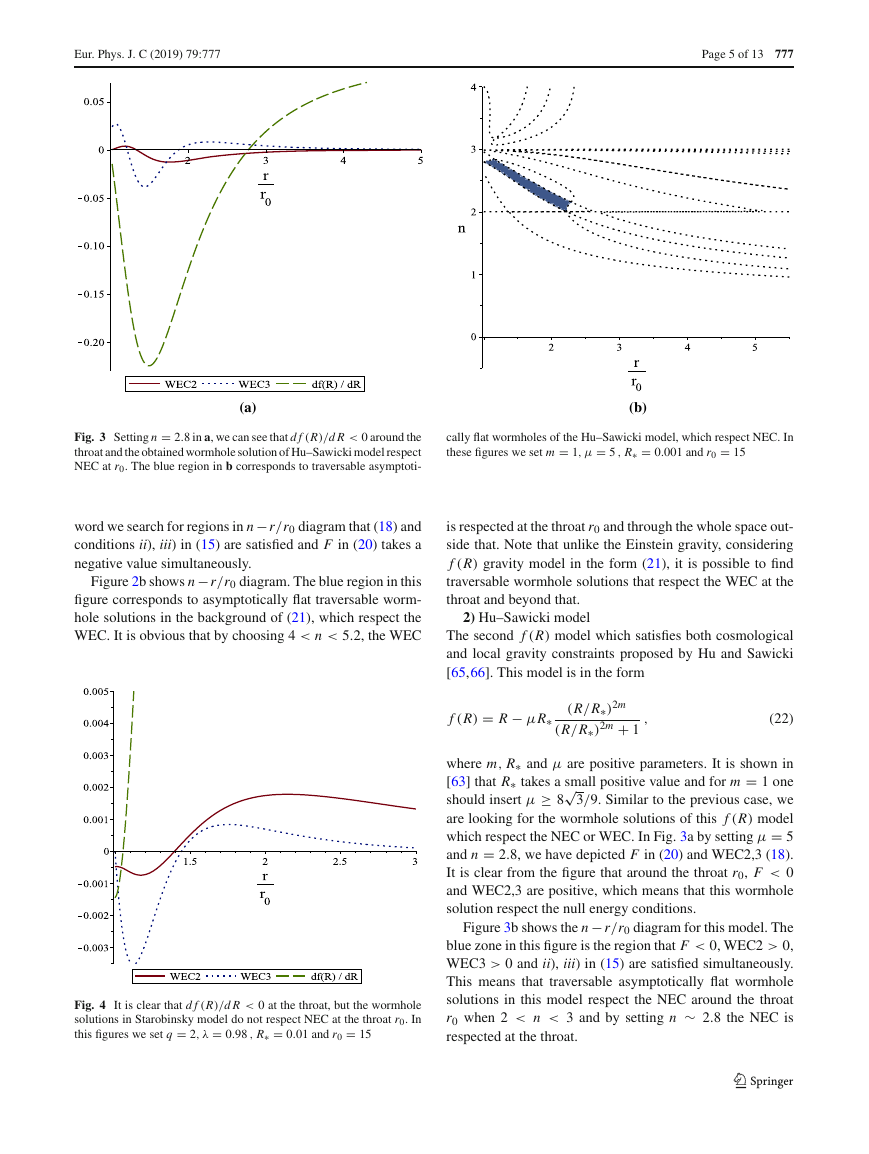
Fig. 3 Setting n = 2.8 in a, we can see that d f (R)/d R < 0 around the
throat and the obtained wormhole solution of Hu–Sawicki model respect
NEC at r0. The blue region in b corresponds to traversable asymptoti-
word we search for regions in n−r/r0 diagram that (18) and
conditions ii), iii) in (15) are satisfied and F in (20) takes a
negative value simultaneously.
Figure 2b shows n−r/r0 diagram. The blue region in this
figure corresponds to asymptotically flat traversable worm-
hole solutions in the background of (21), which respect the
WEC. It is obvious that by choosing 4 < n < 5.2, the WEC
Fig. 4 It is clear that d f (R)/d R < 0 at the throat, but the wormhole
solutions in Starobinsky model do not respect NEC at the throat r0. In
this figures we set q = 2, λ = 0.98 , R∗ = 0.01 and r0 = 15
cally flat wormholes of the Hu–Sawicki model, which respect NEC. In
these figures we set m = 1, μ = 5 , R∗ = 0.001 and r0 = 15
is respected at the throat r0 and through the whole space out-
side that. Note that unlike the Einstein gravity, considering
f (R) gravity model in the form (21), it is possible to find
traversable wormhole solutions that respect the WEC at the
throat and beyond that.
2) Hu–Sawicki model
The second f (R) model which satisfies both cosmological
and local gravity constraints proposed by Hu and Sawicki
[65,66]. This model is in the form
f (R) = R − μR∗
(R/R∗)2m
(R/R∗)2m + 1
,
(22)
where m, R∗ and μ are positive parameters. It is shown in
[63] that R∗ takes a small positive value and for m = 1 one
√
should insert μ ≥ 8
3/9. Similar to the previous case, we
are looking for the wormhole solutions of this f (R) model
which respect the NEC or WEC. In Fig. 3a by setting μ = 5
and n = 2.8, we have depicted F in (20) and WEC2,3 (18).
It is clear from the figure that around the throat r0, F < 0
and WEC2,3 are positive, which means that this wormhole
solution respect the null energy conditions.
Figure 3b shows the n− r/r0 diagram for this model. The
blue zone in this figure is the region that F < 0, WEC2 > 0,
WEC3 > 0 and ii), iii) in (15) are satisfied simultaneously.
This means that traversable asymptotically flat wormhole
solutions in this model respect the NEC around the throat
r0 when 2 < n < 3 and by setting n ∼ 2.8 the NEC is
respected at the throat.
123
777 Page 6 of 13
Eur. Phys. J. C (2019) 79 :777
(a)
(b)
Fig. 5 a Shows that d f (R)/d R < 0 and the NEC is satisfied at the
throat for the wormhole solution of the Nojiri–Odintsov model with
n = 2.8. According to b asymptoticly flat traversable wormholes in
this model, respect NEC by choosing adequate values for n. In these
figures we set m = 2, a = 2, b = 20, c = 20 and r0 = 1
(a)
(b)
Fig. 6 The NEC for a wormhole solution in the case of Amendola–Gannouji–Polarski–Tsujikawa model is respected (a). In the blue part in b,
traversable asymptoticly flat wormholes respect the NEC. In these figures we set μ = 5, R∗ = 0.01, p = 0.5 and r0 = 3
3) The Starobinsky model [65,67,68]
Another viable modified f (R) gravity model that we con-
sider, has three free parameters λ, R∗ and q as:
f (R) = R + λR∗
1 + R2
R2∗
−q − 1
,
(23)
123
where 0.944 < λ < 0.966 for q = 2 according to [63] and
R∗ takes small positive values. Similar to the previous case,
we are looking for the wormhole solutions of this f (R) model
which respect the WEC (18). One can check that by choosing
0.944 < λ < 0.966, F in (20) takes positive values and
there is no static wormhole solution in this model. However
Eur. Phys. J. C (2019) 79 :777
Page 7 of 13 777
(a)
(b)
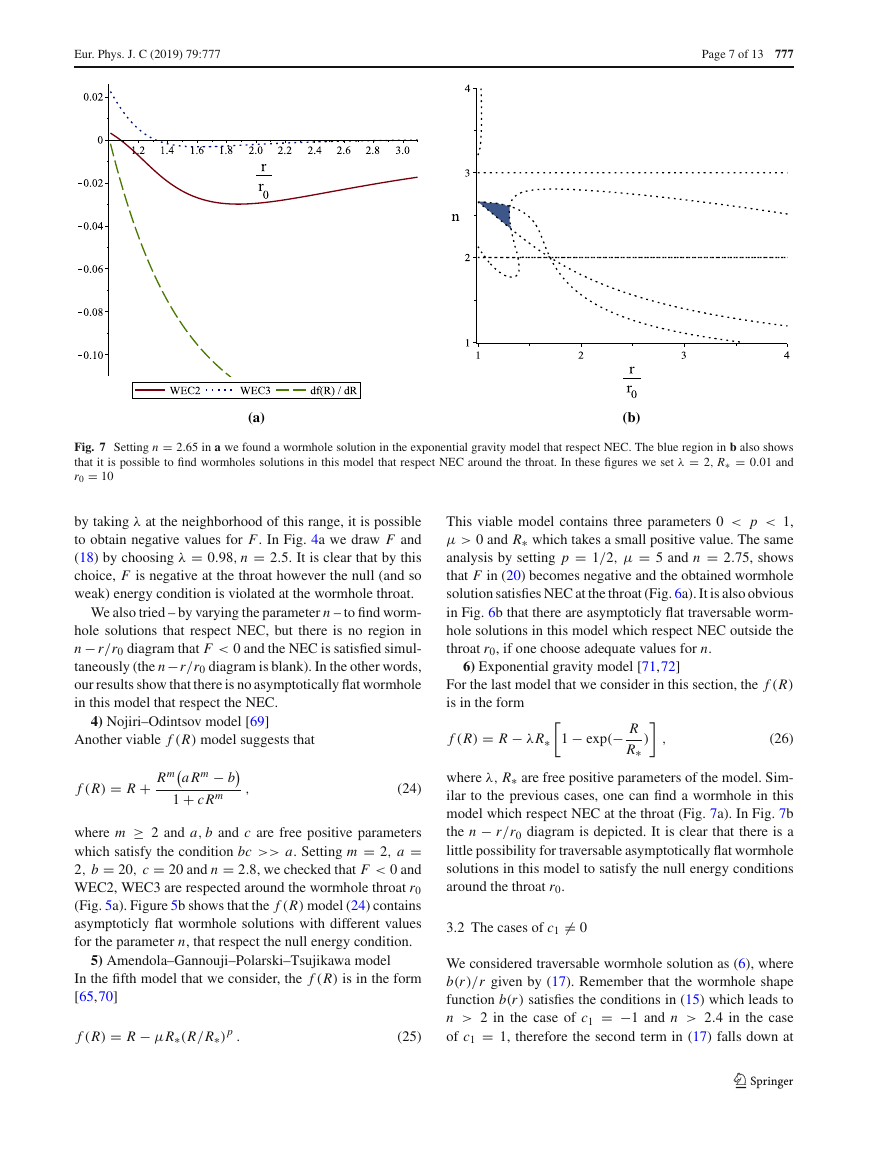
Fig. 7 Setting n = 2.65 in a we found a wormhole solution in the exponential gravity model that respect NEC. The blue region in b also shows
that it is possible to find wormholes solutions in this model that respect NEC around the throat. In these figures we set λ = 2, R∗ = 0.01 and
r0 = 10
by taking λ at the neighborhood of this range, it is possible
to obtain negative values for F. In Fig. 4a we draw F and
(18) by choosing λ = 0.98, n = 2.5. It is clear that by this
choice, F is negative at the throat however the null (and so
weak) energy condition is violated at the wormhole throat.
We also tried – by varying the parameter n – to find worm-
hole solutions that respect NEC, but there is no region in
n − r/r0 diagram that F < 0 and the NEC is satisfied simul-
taneously (the n−r/r0 diagram is blank). In the other words,
our results show that there is no asymptotically flat wormhole
in this model that respect the NEC.
4) Nojiri–Odintsov model [69]
Another viable f (R) model suggests that
a Rm − b
1 + cRm
,
f (R) = R + Rm
(24)
where m ≥ 2 and a, b and c are free positive parameters
which satisfy the condition bc >> a. Setting m = 2, a =
2, b = 20, c = 20 and n = 2.8, we checked that F < 0 and
WEC2, WEC3 are respected around the wormhole throat r0
(Fig. 5a). Figure 5b shows that the f (R) model (24) contains
asymptoticly flat wormhole solutions with different values
for the parameter n, that respect the null energy condition.
This viable model contains three parameters 0 < p < 1,
μ > 0 and R∗ which takes a small positive value. The same
analysis by setting p = 1/2, μ = 5 and n = 2.75, shows
that F in (20) becomes negative and the obtained wormhole
solution satisfies NEC at the throat (Fig. 6a). It is also obvious
in Fig. 6b that there are asymptoticly flat traversable worm-
hole solutions in this model which respect NEC outside the
throat r0, if one choose adequate values for n.
6) Exponential gravity model [71,72]
For the last model that we consider in this section, the f (R)
is in the form
f (R) = R − λR∗
1 − exp(− R
R∗ )
(26)
,
where λ, R∗ are free positive parameters of the model. Sim-
ilar to the previous cases, one can find a wormhole in this
model which respect NEC at the throat (Fig. 7a). In Fig. 7b
the n − r/r0 diagram is depicted. It is clear that there is a
little possibility for traversable asymptotically flat wormhole
solutions in this model to satisfy the null energy conditions
around the throat r0.
3.2 The cases of c1 = 0
5) Amendola–Gannouji–Polarski–Tsujikawa model
In the fifth model that we consider, the f (R) is in the form
[65,70]
f (R) = R − μR∗(R/R∗) p .
(25)
We considered traversable wormhole solution as (6), where
b(r )/r given by (17). Remember that the wormhole shape
function b(r ) satisfies the conditions in (15) which leads to
n > 2 in the case of c1 = −1 and n > 2.4 in the case
of c1 = 1, therefore the second term in (17) falls down at
123
777 Page 8 of 13
Eur. Phys. J. C (2019) 79 :777
(a)
(c)
(b)
(d)
Fig. 8 The blue region in a, c show the asymptotically spherical
(hyperbolic) wormhole solutions of the Tsujikawa model that respect
the NEC. b Which is depicted by setting n = 4.5, r0 = 1, shows
that F = d f (R)/d R < 0 and the asymptotically spherical wormhole
in this model respect NEC around the throat. d Demonstrates that for
an asymptotically open wormhole with n = 2.02, r0 = 0.5, NEC is
respected around the throat. In these figures we set μ = 5, R∗ = 1
large r. In this subsection we choose c1 = ±1, for which the
wormhole metric (6) at large r matches hyperbolic (c1 = −1)
and spherical (c1 = 1) FRW metric, so we call them asymp-
totically hyperbolic and asymptotically spherical wormhole
solutions respectively. In the following we verify the null
and weak energy condition for these asymptotically hyper-
bolic and spherical wormhole solutions in the background of
static f (R) modified gravity models that we considered in
the previous subsection.
1) The Tsujikawa model
For this model the f (R) is given in (21). We are interested
in solutions for which F in (20) takes negative values, condi-
tions ii), iii in (15) are satisfied and (18) are respected simul-
taneously. Figure 8a, c show the location of these asymp-
totically closed (c1 = 1) and open (c1 = −1) wormhole
solutions in the n − r/r0 diagram respectively. In Fig. 8b, d
we have explicitly depicted F and requirements of the WEC
for an asymptotically spherical (hyperbolic) wormhole solu-
tion with n = 4.5 (n = 2.02). It is obvious that by choosing
adequate values for the parameters, one can find traversable
123
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
