logo资料库

信息论课件完整版.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：3.91M 资料格式：pdf 举报 版权申诉
第1页 / 共59页
第2页 / 共59页
第3页 / 共59页
第4页 / 共59页
第5页 / 共59页
第6页 / 共59页
第7页 / 共59页
第8页 / 共59页
资料共59页，剩余部分请下载后查看
    ch00.article.pdf
    本课程主要内容
    参考资料
    考核方法
    网络资源
    ch01.article.pdf
    信息论简介
    什么是信息？
    信息的特性
    信息、消息、信号之间的关系
    通信系统模型
    通信系统详细模型
    什么是信息论？
    信息论研究的对象
    信息论的分支
    信息论的应用
    信息论的发展历史
    ch02.article.pdf
    概率论回顾
    Lagrange 乘数法
    自信息量
    互信息量
    互信息量的性质
    条件互信息量
    离散集的平均自信息量
    熵函数的性质
    离散集的平均互信息量
    ch03.article.pdf
    信源的分类和建模
    离散平稳信源的熵率
    离散马尔可夫信源及其熵率
    离散马尔可夫信源
    离散马尔可夫信源的熵率
    ch04.article.pdf
    综述
    信道分类
    信道模型
    信道疑义度
    平均互信息量及其性质
    信道容量
    离散无记忆信道容量定理
    信道容量的计算
    离散无噪信道的信道容量计算
    离散对称信道的信道容量计算
    信道矩阵可逆的信道容量求法
    拉格朗日乘数法
    信道容量的迭代计算法
    数据处理定理
    信道的组合
    ch05.article.pdf
    渐进等同分割性
    定长无失真信源编码定理
    无失真变长编码
    Kraft 不等式
    唯一可译码判决准则
    变长信源编码定理
    无失真信源编码技术
    Huffman 编码算法
    Shannon 编码算法
    Shannon-Fano-Elias 编码算法
    Fano 编码算法
    Huffman 编码的几个问题
    算数编码
    游程编码
    通用编码
    几种编码方案的性能对比
    ch06.article.pdf
    综述
    失真测度
    平均失真
    信息率失真函数
    D* 失真许可信道
    信息率失真函数的定义
    信息率失真函数 R(D) 的性质
    限失真信源编码定理和逆定理
    限失真信源编码定理
    限失真信源编码逆定理
    熵压缩编码具体方法
    标量量化
    矢量量化
    变换编码
    预测编码
    ch07.article.pdf
    信道编码
    信道编码的分类
    信道译码准则
    信道编码定理
    Fano 不等式
    assignment.pdf
    信息论基础 — 课程基本信息 李亦农 hoplee@bupt.edu.cn 1 本本本课课课程程程主主主要要要内内内容容容 本本本课课课程程程主主主要要要内内内容容容 • 绪论 • 信息论的基本概念 • 离散信源 • 离散信道 • 无失真信源编码 • 有噪信道编码 • 限失真信源编码 2 参参参考考考资资资料料料 参参参考考考资资资料料料 • Elements of Information Theory, Thomas M. Cover, Joy A. Thomas, 清华大学出版社，ISBN 7-302-07285-X • 《信息论基础教程》 李亦农 李梅 编著，北京邮电大学出版社，ISBN 7-5635-0910-0 • 《应用信息论基础》 朱雪龙 编著，清华大学出版社，ISBN 7-302-04154-7 • 《信息论基础》 周荫清 主编，北航出版社，北京邮电大学翻印 • 《信息论—基础理论与应用》 傅祖芸 编著，电子工业出版社，ISBN 7-5053-6850-8/TP·3878 • 《信息论及其应用》 仇佩亮 编著，浙江大学出版社，ISBN 7-308-02124-6/G201 3 考考考核核核方方方法法法 考考考核核核方方方法法法 • 作业：20% • 上机：20% • 期末考试：60% 1
    4 网网网络络络资资资源源源 网网网络络络资资资源源源 • 本课程相关的幻灯片讲义、作业、上机题和阅读材料： ftp://202.112.10.142/HopLee/InformationTheory/ 2
    ɞ9Ạ —  ʢȇ hoplee@bupt.edu.cn ᑁᑁᑁ LLL 1 ɞɞɞ 1.1 ʖɞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2 ɞḄᱯឋ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.3 ɞஹɞஹ5_Ḅᐵ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.4 ΅ɂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.5 ΅ɂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.6 ʖɞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.7 ɞẆḄ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.8 ɞḄᑖʌ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.9 ɞḄᵨ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 ɞɞɞḄḄḄ555ᔊᔊᔊ555 1 ɞɞɞ 1.1 ʖʖʖɞɞɞ ʖʖʖɞɞɞ I 1 1 1 2 2 3 3 3 4 4 4 • ΅ᙢɞʖOɞ஺ • ᙢɞʖᱥᙠȤ4Ḅ̶?஺ɞᙠ_ḄȊ̠ʖʠ ஺ • Hᙢɞʖ◀̒ឋᡠϛSḄ΁஺ ʖʖʖɞɞɞ II 1.2 ɞɞɞḄḄḄᱯᱯᱯឋឋឋ ɞɞɞḄḄḄᱯᱯᱯឋឋឋ • ɞʖAḄ஺ • ɞʖ5ᐳḄ஺ • ɞʖA▲Ḅ஺ • ɞʖ5[Ḅ஺ 1
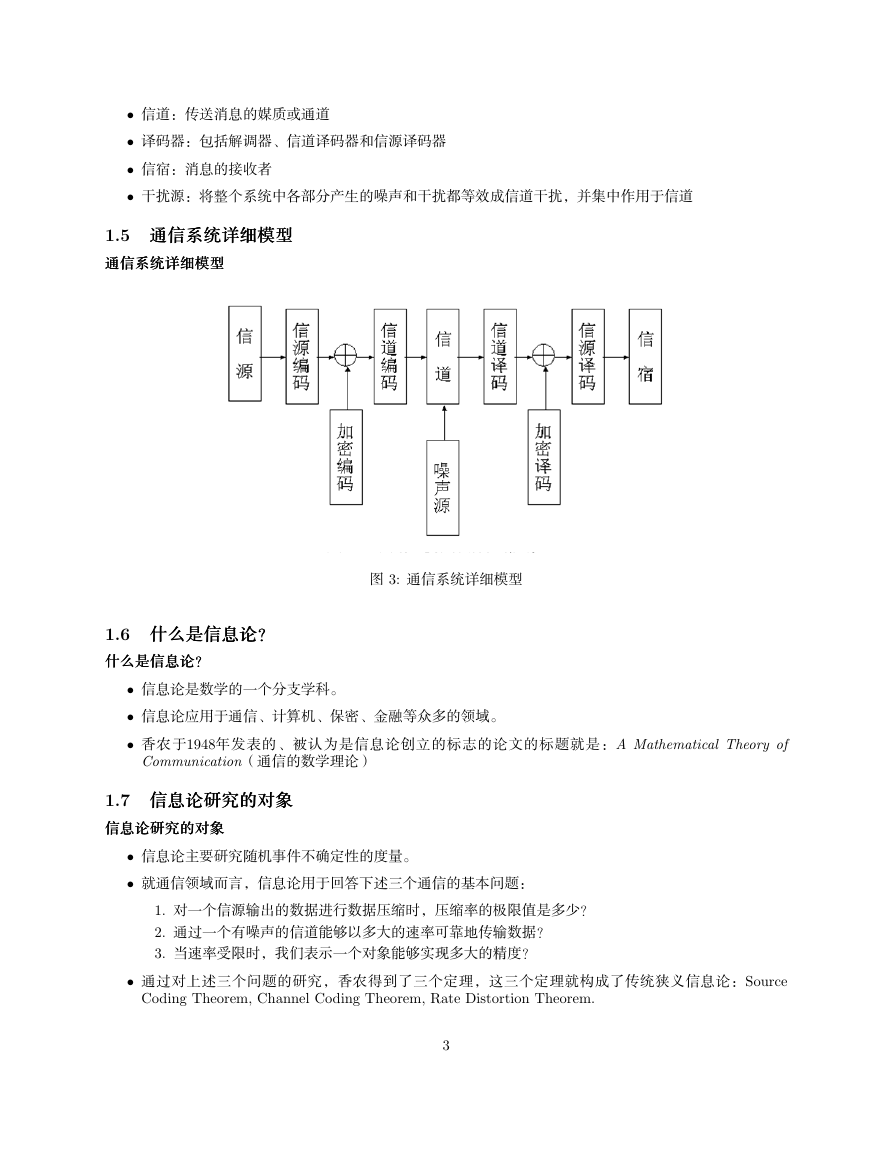
    8 1: ɞḄᭆ 1.3 ɞɞɞஹஹஹɞɞɞஹஹஹ555___ḄḄḄᐵᐵᐵ ɞɞɞஹஹஹɞɞɞஹஹஹ555___ḄḄḄᐵᐵᐵ • ɞʖɞḄ₹ὅ஺ɞᐹᨵȜḄஹᦻஹ5ஹᦪɼஹ8ᱏ஺ • ᪀ᡂɞ⌕ᩩ – PX΅5AᡠᳮY – 5ᙠ΅⌴Ȥᣚ • ȜɞȜḄᩭ5ȞᨵȜḄɞ[Ȝɞ5ᵨȜḄɞᩭ₹஺ • 5ʖɞḄ⊤Iɞʖ5Ḅᐹᑁ஺ • 5ʖ⊤̙ɞḄᱥᳮ[ᒹ>:ஹᐝஹᵯ5ஹʡD5஺ 1.4 ΅΅΅ɂɂɂ ΅΅΅ɂɂɂ I 8 2: ΅9ʠɂ ΅΅΅ɂɂɂ II • ˯ɞḄ • ṹᘤᒹ>ṹᘤஹ⍝ṹᘤȤᑴᘤ 2
    • ⍝〈ɞḄᡈ΅⍝ • ṹᘤᒹ>Yᘤஹ⍝ṹᘤȤṹᘤ • ɞḄ?ᦈὅ • ᡾᦮ᔜZᑖ˯Ḅȶ:Ȥ᡾Zᦔᡂ⍝᡾`ᵨ⍝ 1.5 ΅΅΅ɂɂɂ ΅΅΅ɂɂɂ 8 3: ΅ɂ 1.6 ʖʖʖɞɞɞ ʖʖʖɞɞɞ • ɞʖᦪḄᑖʌO஺ • ɞᵨ΅ஹʡஹஹ[ͮɏḄ⚞9஺ • ✏ȇ19485⊤ḄஹXʖɞȉḄ᪗ḄᦻḄ᪗⚪ʖA Mathematical Theory of Communication΅Ḅᦪᳮ 1.7 ɞɞɞẆẆẆḄḄḄ ɞɞɞẆẆẆḄḄḄ • ɞ⌕Ẇψʡ̒ឋḄ[஺ • ΅⚞9̠ɞᵨ8΅Ḅ9ʠ_⚪ 1. 3ḄᦪɼʹᦪɼȚAȚ᳛Ḅ᩽▲Ƿʖɏ 2. ΅ᨵȶ:Ḅ⍝PɏɏᜧḄ΅᳛5☠ᙢᦪɼ 3. ΅᳛5▲Aᡃ⊤̙PɏIɏᜧḄ • ΅_⚪ḄẆ✏ȇᑮᳮᳮ᪀ᡂHɞSource Coding Theorem, Channel Coding Theorem, Rate Distortion Theorem. 3
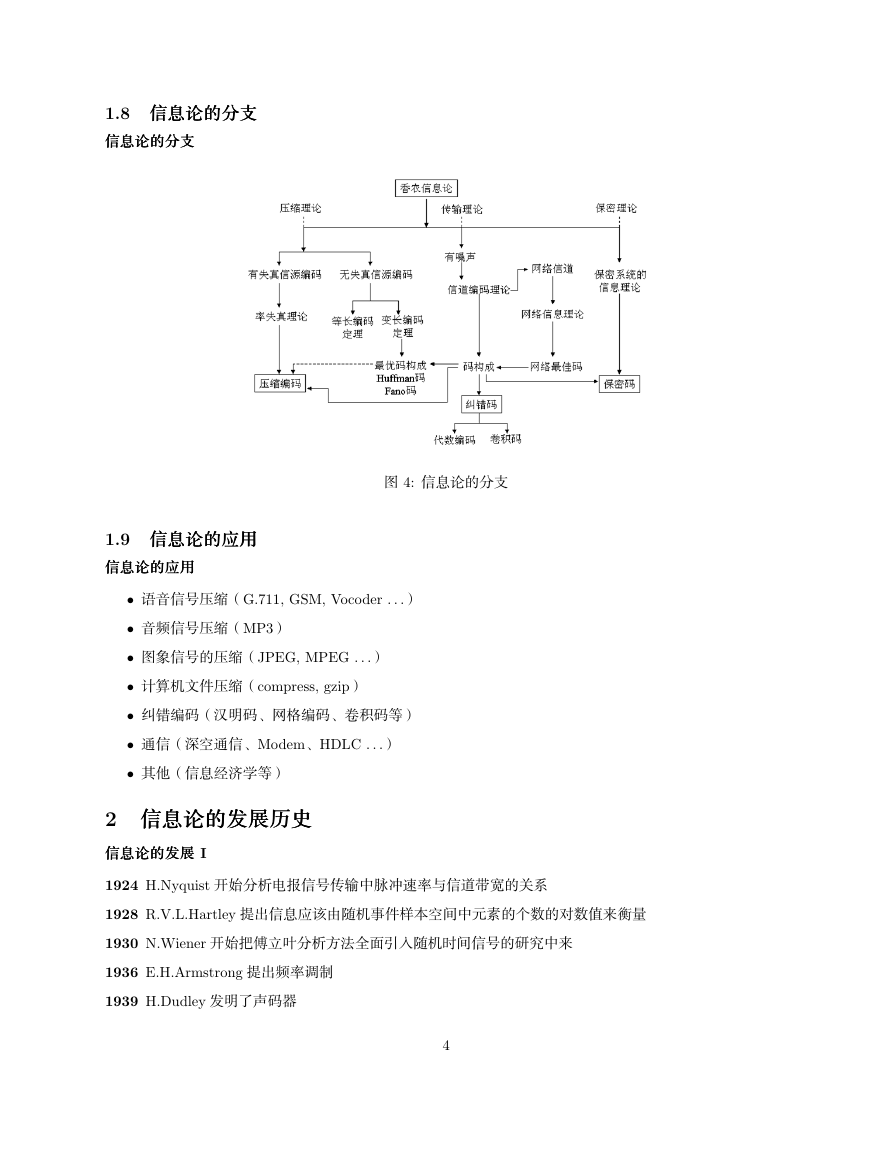
    1.8 ɞɞɞḄḄḄᑖᑖᑖʌʌʌ ɞɞɞḄḄḄᑖᑖᑖʌʌʌ 8 4: ɞḄᑖʌ 1.9 ɞɞɞḄḄḄᵨᵨᵨ ɞɞɞḄḄḄᵨᵨᵨ • a5ȚG.711, GSM, Vocoder . . . • a⚣5ȚMP3 • 85ḄȚJPEG, MPEG . . . • ʡᦻȚcompress, gzip • ┯ṹʔṹஹʫṹஹᔁOṹ • ΅΅ஹModemஹHDLC . . . • ᐸɞ 2 ɞɞɞḄḄḄ555ᔊᔊᔊ555 ɞɞɞḄḄḄ555 I 1924 H.Nyquist ;ᑖ᪆ᵯ>5ᾭ3΅᳛⍝Ḅᐵ 1928 R.V.L.Hartley ?3ɞᵫψʡ᪵ʠ_ᐗḄᦪḄᦪǷᩭ⊝[ 1930 N.Wiener ;ɴᏝ5ᑖ᪆Aᐰ☢ᐭψʡA_5ḄẆᩭ 1936 E.H.Armstrong ?3⚣᳛ᑴ 1939 H.Dudley 5ʔ:ṹᘤ 4
    1948 N.Wiener 5⊤Ĭ?ᑴĬ 1948 C.E.Shannon 5⊤Ĭ΅ḄᦪᳮĬ 1952 D.A.Huffman ?3 Huffman ṹ ɞɞɞḄḄḄ555 II 1954 P.Elias ?3ᔁOṹ 1959 S.K.Kullback ?3␺ȊɞḄᭆ 1961 C.E.Shannon ?3ɏᵨᡝɞ 1963 P.Elias ?3ʠṹ 1965 A.N.Kolmogorov ?3΅ᵨṹ 1982 G.Ungerboeck Iʫṹᑴ 1993 Turbo ṹḄឋPϏ?ᳮ᩽▲ 5
    信息论基础 — 信息论的基本概念 李亦农 hoplee@bupt.edu.cn 内内内容容容简简简介介介 目目目录录录 1 概概概率率率论论论回回回顾顾顾 2 Lagrange 乘乘乘数数数法法法 3 自自自信信信息息息量量量 4 互互互信信信息息息量量量 4.1 互信息量的性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.2 条件互信息量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 离离离散散散集集集的的的平平平均均均自自自信信信息息息量量量 5.1 熵函数的性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 离离离散散散集集集的的的平平平均均均互互互信信信息息息量量量 1 概概概率率率论论论回回回顾顾顾 概概概率率率论论论回回回顾顾顾 1 3 3 4 4 4 5 6 7 • 离散随机变量（Discrete Random Variables） 假设 X 是一个随机变量，它的取值空间是一个包含 m 个不同元素的集合 X = {v1, v2, . . . , vm}。pi 表 示变量 X 取值为 vi 的概率：pi = Pr{x = vi}。那么，pi 满足 pi 0 以及 pi = 1。 • 期望值（Expected Value） X 的取值 x 的均均均值值值、期期期望望望值值值或平平平均均均值值值定义如下： i i vipi xp(x) = x∈X • 二次矩（Quadratic Matrix） X 的取值 x 的二二二次次次矩矩矩和方方方差差差定义如下： E[X] = µ = x∈X E[X 2] = x2p(x) V ar[X] = E[(x − µ)2] = σ2 = x∈X (x − µ)2p(x) 上式中 σ 称为 X 的标标标准准准偏偏偏差差差 1 (1) (2) (3)
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料