第37卷第1期安徽理工大学学报(自然科学版)Vol．37No．12017年1月JournalofAnhuiUniversityofScienceandTechnology(NaturalScience)Jan．2017利用Poisson过程分析公共停车场的停车问题殷月竹，殷志祥，许峰(安徽理工大学数学与大数据学院，安徽淮南232001)摘要:针对目前我国城市中公共停车场的"停车难"、"停车乱"的问题，研究如何科学地规划建设城市公共停车场，从而为解决城市停车问题提供理论和实践依据。运用排队论和Pois-son过程对公共停车场的停车情况进行分析，并建立具体的模型。通过对实例的计算验证了公共停车场的车辆到达的间隔时间服从Poisson分布，并通过解随机微分方程组求出了排队等待停车位的车辆数的数学期望和方差，以及服务时间的数学期望和方差，最后对所建模型进行了分析与总结，结果表明该模型是正确且有实用价值的。关键词:公共停车场;排队论;Poisson过程;停车难中图分类号:O226，U491.7文献标志码:A文章编号:1672－1098(2017)01－0016－04收稿日期:2016－09－18基金项目:国家自然科学基金(No．61170172，61073102)作者简介:殷月竹(1980－)，女，山东日照人，讲师，硕士，研究方向:随机过程、最优控制。UsePoissonProcesstoAnalyzeParkingProblemsofPublicCarParksYINYue－zhu，YINZhi－xiang，XUFeng(SchoolofMathematicsandBigData，AnhuiUniversityofScienceandTechnology，HuainanAnhui232001，China)Abstract:Inthispaper，thecurrentproblemsofdifficultyinparkingandillegalparkingatpubliccarparksinChinesecitiesaswellashowtoscientificallyplanandbuildpubliccarparksarestudied，soastoprovidethetheoryandpracticebasisforsolvingtheproblemsofcityparking．AndtheparkingsituationofpubliccarparksbyPoissonprocessandqueuingtheoryisanalyzedtobuildaspecificmodel．Thefactthatthearrivaltimeinter-valsofcarsinpubliccarparksobeyPoissondistributionhasbeenverifiedthroughthecalculationofalivingex-ample．Bysolvingthestochasticdifferentialequations，themathematicalexpectationandvarianceofthenumberofvehiclestowaitforparkingspacearefoundout，andthemathematicalexpectationandvarianceofservicetimearealsofoundout．Finally，themodelisanalyzedandsummarized，andtheresultsshowthatthemodelisrightandvaluable．Keywords:publiccarparks;Poissonprocess;queuingtheory;difficultycityparking目前，随着我国经济的迅速发展和人们生活水平的大力提高，机动车辆尤其是私家车越来越多。这不仅带来严重的交通堵塞问题，而且也使得公共停车场车位不足导致车辆乱停乱放、引发交通事故等问题。公共停车场是为从事各类活动的开车出行者提供停车服务的场所。目前，我国城市的公共停车场存在一些问题，例如规划布局和设置不合理、利用率不高或停车拥挤杂乱［1－3］。这些问题，有些是停车政策和管理导致的，更根本的原因是缺少科学的规划建设。对公共停车场进行科学合理中国煤炭期刊网 www.chinacaj.net

的规划建设是解决当前城市泊车问题的关键。停车需求预测分析也是城市公共停车场规划和实现供需平衡的重要依据［4－7］。目前，关于城市公共停车场供需平衡问题的研究主要有总量预测法、费用效益分析法、回归分析模型和时间序列模型等方法［8－12］，但这些方法和模型因其静态性、确定性而导致准确性不够。本文采用随机动态理论———排队论［13－14］和Poisson过程［15－16］对该问题进行研究，给出了具体的模型，并以淮南市某公共停车场为实例，作了实证分析和研究，提出了淮南市公共停车场的发展策略，有助于改善淮南市的停车状况，为今后的城市公共停车场的建设和管理提供理论和实践依据。1建立模型1．1分析公共停车场停车情况对公共停车场的停车情况采用排队论进行分析，所假定的排队系统有以下三个基本组成部分1)输入过程，即车辆到达公共停车场的过程。其特征是:车辆的总体是无限的，车辆的到达方式是一个接一个且是相互独立的，车辆相继到来的时间间隔是随机的，输入过程是平稳的。2)服务机制，其特征是:有多个服务台且是平行设置的;服务方式是每个车位每次只对一个车辆进行服务;服务时间是随机的，其分布是平稳的。3)排队规则，其服务规则是“先到先服务”，即按照到达的先后次序接受服务;车辆到达时，若所有停车位均被占用，则当即离开;队列排在具体的场所，其数目是多列，并且公共停车场的最大容量有限。1．2Poisson过程Poisson过程是一类时间连续、状态离散的随机过程。若以某时刻为初始0时刻，且假设在这之前，公共停车场无车;随着时间的推移，停车的数量逐渐增多;因为相邻时刻车辆的到达两两相互独立，即停车的可能性互不影响，所以车辆到达的过程符合Poisson过程的特点。设X(t)表示在时间间隔［0，t］(t＞0)内到来的车辆数，设Pn(t1，t2)表示在时间间隔［t1，t2］(t2＞t1)内有n辆车到来的概率，即Pn(t1，t2)=P{X(t2)－X(t1)=n}(1)则当满足下面三个条件时，车辆到达的过程服从Possion过程。1)独立性:在互不相交的间隔时间内车辆到达的情况是相互独立的;2)平稳性:对于很短的时间增量Δt，在时间间隔［t，t+Δt］内有1辆车到来的概率与Δt成正比，而与t无关;3)普通性:时间间隔［t，t+Δt］内多余1个车辆到达的概率很小很小，即∑∞n=2Pn(t，t+Δt)=ο(Δt)。在上述条件下，可得在时间间隔［0，t］有n辆车到达的概率Pn(t)为Poisson分布，即车辆到达的间隔时间服从Poisson分布Pn(t)=(λt)ne－λtn!(2)式中:λ为参数，n=0，1，2，…。1．3车辆数和服务时间的数学期望和方差在排队系统M/M/s中，假设有s个服务台(即停车位)，车辆到达的间隔时间服从参数为λ1的Poisson分布，服务时间服从参数为λ2的指数分布。车辆的到达和被服务均是相互独立、随机的。当所有的停车位在t时刻都被占满时，有一个停车位将在［t，t+Δt］内空闲出来提供服务的概率为sλ2Δt+ο(Δt)。设X(t)为t时刻的车辆数，且在初始时刻t=0时X(0)=i，则转移条件概率Pi，j(0，t)=P{X(t)=j|X(0)=i}j=1，2，…(3)它满足下列差分方程式dPi，0(0，t)dt=－λ1Pi，0(0，t)+λ2Pi，1(0，t)(4)dPi，j(0，t)dt=λ1Pi，j－1(0，t)－(λ1+jλ2)Pi，j(0，t)+(j+1)λ2Pi，j+1(0，t)(j=1，2，…，s－1)(5)dPi，j(0，t)dt=λ1Pi，j－1(0，t)－(λ1+sλ2)Pi，j(0，t)+sλ2Pi，j+1(0，t)(j=s，s+1，…)(6)71第1期殷月竹，等:利用Poisson过程分析公共停车场的停车问题中国煤炭期刊网 www.chinacaj.net

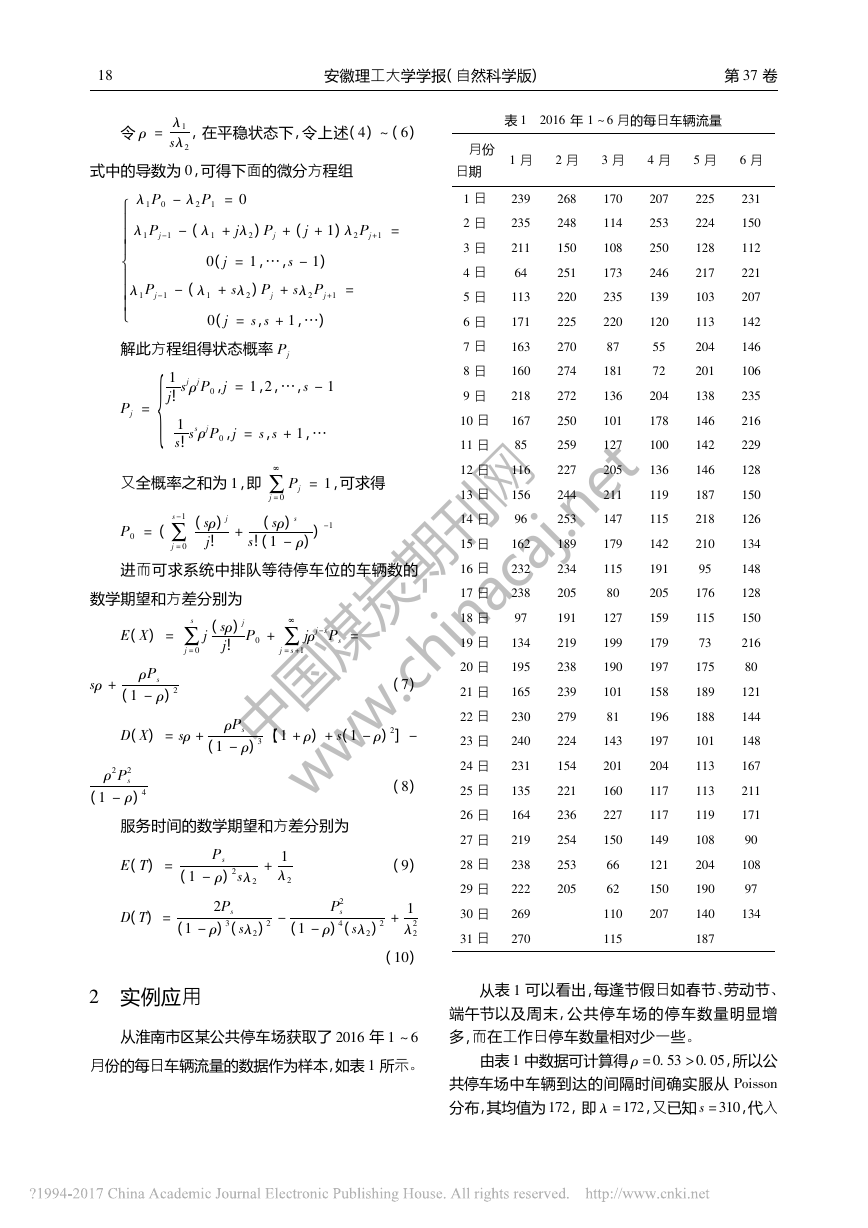
令ρ=λ1sλ2，在平稳状态下，令上述(4)～(6)式中的导数为0，可得下面的微分方程组λ1P0－λ2P1=0λ1Pj－1－(λ1+jλ2)Pj+(j+1)λ2Pj+1=0(j=1，…，s－1)λ1Pj－1－(λ1+sλ2)Pj+sλ2Pj+1=0(j=s，s+1，…)解此方程组得状态概率PjPj=1j!sjρjP0，j=1，2，…，s－11s!ssρjP0，j=s，s+1{，…又全概率之和为1，即∑∞j=0Pj=1，可求得P0=(∑s－1j=0(sρ)jj!+(sρ)ss!(1－ρ))－1进而可求系统中排队等待停车位的车辆数的数学期望和方差分别为E(X)=∑sj=0j(sρ)jj!P0+∑∞j=s+1jρj－sPs=sρ+ρPs(1－ρ)2(7)D(X)=sρ+ρPs(1－ρ)3［(1+ρ)+s(1－ρ)2］－ρ2P2s(1－ρ)4(8)服务时间的数学期望和方差分别为E(T)=Ps(1－ρ)2sλ2+1λ2(9)D(T)=2Ps(1－ρ)3(sλ2)2－P2s(1－ρ)4(sλ2)2+1λ22(10)2实例应用从淮南市区某公共停车场获取了2016年1～6月份的每日车辆流量的数据作为样本，如表1所示。表12016年1～6月的每日车辆流量月份日期1月2月3月4月5月6月1日2392681702072252312日2352481142532241503日2111501082501281124日642511732462172215日1132202351391032076日1712252201201131427日16327087552041468日160274181722011069日21827213620413823510日16725010117814621611日8525912710014222912日11622720513614612813日15624421111918715014日9625314711521812615日16218917914221013416日2322341151919514817日2382058020517612818日9719112715911515019日1342191991797321620日1952381901971758021日16523910115818912122日2302798119618814423日24022414319710114824日23115420120411316725日13522116011711321126日16423622711711917127日2192541501491089028日2382536612120410829日222205621501909730日26911020714013431日270115187从表1可以看出，每逢节假日如春节、劳动节、端午节以及周末，公共停车场的停车数量明显增多，而在工作日停车数量相对少一些。由表1中数据可计算得ρ=0.53＞0.05，所以公共停车场中车辆到达的间隔时间确实服从Poisson分布，其均值为172，即λ=172，又已知s=310，代入81安徽理工大学学报(自然科学版)第37卷中国煤炭期刊网 www.chinacaj.net

(7)、(8)式得车辆的期望值和方差分别为E(X)=175D(X)=6396进一步计算得该公共停车场提供服务的车位在区间范围(槡175－6396，槡175+6396)内，即(95，255)。服务时间的数学期望和方差分别为E(T)=1.20D(T)=0.015进而可计算得服务时间在区间范围(1.20－槡0.015，槡1.20+0.015)，即(1.08，1.32)。据此计算结果分析如下:2016年1～6月份，该公共停车场提供服务的车量平均值为175，上下波动幅度为80，即最少为95辆，最多为255辆。公共停车场的每个停车位对每辆车的平均服务时间是1.20，上下波动幅度为0.12，即最少为1.08，最多为1.32。据此可得，停车位的数量可确定为100～320位，所以实际提供的310个车位在此范围内，目前既能满足停车需要又不会过剩太多，而且现实中随着私家车的进一步增长，停车需求也会进一步增加，说明提供310个车位是比较合理的。实际应用中可以根据季节变动、节假日和其它影响停车需求的因素对提供的停车位作适当调整，使之既能满足需要又能节约成本。分析可知，该模型统计得出的数据与实际情况基本相符，对实际的公共停车场的建设和管理具有一定的参考价值和指导意义。3总结分析该模型采用动态随机服务系统理论———排队论和Poisson过程对公共停车场的停车情况进行分析，克服了静态方法的缺点，更加符合实际情况，既最大限度地满足了停车需要，又不过剩浪费，有利于提高公共停车场的物业管理效益。为城市公共停车场的决策分析、规划与建设提供了理论指导和实践依据。该模型的不足之处是限定了公共停车场车辆的到来方式是单个的、独立的，事实上车辆的到来方式可能是成批的，也可能是相关联的;此外，该模型所假定的服务时间分布的平稳性也影响了其对现实的适应性。参考文献:［1］郭学琴．城市公共停车场规划研究［D］．北京:北京交通大学，2007．［2］陈峻．城市停车设施规划方法研究［D］．南京:东南大学，2000．［3］过文魁，刘树斌．大城市公共停车场建设困境与对策－以杭州市为例［J］．城市交通，2015(4):37－43．［4］甘勇华，陈先龙．适应新形势的大城市停车需求预测方法［J］．土木工程与管理学报，2012，29(1):85－88．［5］邹成伟，胡宝雨，王彪．城市公共停车场停车需求预测方法研究及应用［J］．公路，2014(8):147－150．［6］吴德华．基于现状调查的城市老城区停车需求预测方法［J］．交通运输系统工程与信息，2014，14(1):235－241．［7］薛行健，欧心泉，晏克非．基于泊位共享的新城区停车需求预测［J］．城市交通，2010，8(5):52－56．［8］KOBUSMBW，GUTIRREZ－I－PUIGARNAUE，RIETVELDP，etal．Theon－streetparkingpremiumandcardrivers＇choicebetweenstreetandgarageparking［J］．RegionalScience＆UrbanEconomics，2013，43(2):395－403．［9］刘姝驿，乔宏，杨庆媛，等．重庆解放碑商圈停车位配置问题分析［J］．西南大学学报(自然科学版)，2014，36(4):120－126．［10］刘松尧，吕建新．基于成本－效益分析的公共停车场建设评估模型［J］．城市交通，2007，5(3):58－61．［11］刘庆．中心商业区公共停车场选址模型研究［D］．哈尔滨:哈尔滨工业大学，2010．［12］JIY．Availableparkingspaceoccupancychangechar-acteristicsandshort－termforecastingmodel［J］．Jour-nalofSoutheastUniversity，2007，23(4):604－608．［13］宋学峰，魏晓平．运筹学［M］．南京:东南大学出版社，2006:329－337．［14］周维，杨鹏飞．运筹学［M］．北京:科学出版社，2008:235－238．［15］贾波涛．Poisson过程的推广及其应用［D］．武汉:华中科技大学，2010．［16］BOUCHERJP，COUTURE－PICHG．Modelingthenumberofinsureds＇carsusingqueuingtheory［J］．In-suranceMathematics＆Economics，2015，64(96):67－76．(责任编辑:李丽，吴晓红，编辑:丁寒)91第1期殷月竹，等:利用Poisson过程分析公共停车场的停车问题中国煤炭期刊网 www.chinacaj.net