第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
OPA图像隐写算法 Secure Steganographic Methods for Palette Images.pdf
1 Introduction
2 Message Hiding Using the Parity of Palette Colors
3 Optimal Parity Assignment
3.1 Algorithm for Optimal Parity Assignment
3.2 Multiple-Pixel Embedding
4 Adaptive Methods
Embedding while Dithering
6 Conclusion and Future Directions
Acknowledgements
References
Secure Steganographic Methods for Palette Images
Jiri Fridrich and Rui Du
Center for Intelligent Systems, Dept. of SS&IE,
SUNY Binghamton, Binghamton, NY 13902-6000
{fridrich,bh09006}@binghamton.edu
it can be used for
Abstract. In this paper, we study non-adaptive and adaptive steganographic
techniques for images with low number of colors in palette image formats. We
have introduced the concept of optimal parity assignment for the color palette
and designed an efficient algorithm that finds the optimal parity assignment.
The optimal parity is independent of the image histogram and depends only on
the image palette. Thus,
increasing the security of
steganographic techniques that embed message bits into the parity of palette
colors. We have further developed two adaptive steganographic methods
designed to avoid areas of uniform color and embed message bits into texture-
rich portions of the cover image. Both techniques were tested on computer
generated images with large areas of uniform color and with fonts on uniform
background. No obvious artifacts were introduced by either technique. The last,
embedding-while-dithering, technique has been designed for palette images
obtained from true color images using color quantization and dithering. In this
technique, both the color quantization error and the error due to message
embedding are diffused through the image to avoid introducing artifacts
inconsistent with the dithering algorithm.
1
Introduction
The purpose of steganography is to hide messages in otherwise innocent looking
carriers. The purpose is to achieve security and privacy by masking the very presence
of communication. Historically, the first steganographic techniques included invisible
writing using special inks or chemicals. It was also fairly common to hide messages in
text. By recovering the first letters from words or sentences of some innocent looking
text, a secret message was communicated. Today, it seems natural to use binary files
with certain degree of irrelevancy and redundancy to hide data. Digital images,
videos, and audio tracks are ideal for this purpose.
Each steganographic technique consists of an embedding algorithm and a detector
function. The embedding algorithm is used to hide secret messages inside a cover (or
carrier) document. The embedding process is usually protected by a keyword so that
only those who posses the secret keyword can access the hidden message. The
detector function is applied to the stego-document and returns the hidden secret
message. For secure covert communication, it is important that by injecting a secret
message into a cover document no detectable changes are introduced. The main goal
is to not raise suspicion and avoid introducing statistically detectable modifications
A. Pfitzmann (Ed.): IH´99, LNCS 1768, pp. 47-60, 2000.
Springer-Verlag Berlin Heidelberg 2000
48
Jiri Fridrich and Rui Du
into the stego-document. The embedded information is undetectable if the image with
the embedded message is consistent with the model of the source from which the
cover images are drawn. We point out that the ability to detect the presence does not
automatically imply the ability to read the hidden message. We further note that
undetectability should not be mistaken for invisibility − a concept tied to human
perception. At present, the formal theoretical framework for steganography similar to
Shannon information theory is still missing. For a comprehensive treatment of this
topic, see [1].
the cover
the probability that
image and the higher
The undetectability is directly influenced by the size of the secret message and the
format and content of the cover image. Obviously, the longer the message, the larger
the modification of
the
modifications can be statistically detected. The choice of the cover image is also
important. Natural photographs with 24 bits per pixel provide the best environment
for message hiding. The redundancy of the data helps to conceal the presence of
secret messages. Image formats that utilize color palettes provide efficient storage for
images with limited number of colors, such as charts, computer art, or color quantized
true color images. The palette image format GIF is recognized by all browsers and is
widely used over the Internet. Posting a GIF file on one's web page will undoubtedly
raise less suspicion than sending an image in the BMP format. Despite their
usefulness and advantages, palette images provide a hostile environment for the
steganographer. The limited number of palette colors makes the process of secure
message hiding a difficult challenge. The most common steganographic technique −
the least significant bit embedding (LSB) cannot be directly applied to palette images
because too many new colors would be created. Most current steganographic
algorithms for palette images introduce easily detectable artifacts in the palette or in
the image data [8,9].
On the highest level, the typical palette image format consists of three parts: a
header, a palette, and image data or pointers to the palette. The palette contains the
RGB triplets of all colors that occur in the image. Secret messages can be hidden
either in the palette itself or in the image data. Gifshuffle [10] is a program that uses
the palette order to hide up to log2(256!)=210 bytes in the palette by permuting its
entries. While this method does not change the appearance of the image, which is
certainly an advantage, its security is weak because many image processing software
products order the palette according to luminance, frequency of occurrence, or some
other scalar factor. A randomly ordered palette is suspicious, which goes against the
basic requirement of secure steganography. Also, displaying the image and resaving it
may erase the information because the palette may be reordered. An alternative and
perhaps more secure approach is to hide encrypted messages in the LSBs of the
palette colors. In order to make the message readable from an image with a reordered
palette, care needs to be taken during message embedding so that the message is
readable at the receiving end. The common disadvantage of all techniques that embed
message bits into the palette is a rather limited capacity independent of the image size.
Practical methods should have capacity proportional to the image size, or the
number of pixels. Many currently available software tools [3,4,7,10−13] decrease the
Secure Steganographic Methods for Palette Images
49
color depth of the GIF image to 128, 64, or 32 before the embedding starts. This way,
when the LSBs of one, two or three color channels are perturbed, the total number of
newly created colors will be at most 256. Thus, it will be possible to embed one, two,
or three bits per pixel without introducing visible artifacts into the cover image.
However, as pointed out by Johnson [8,9], the new palettes will have easily detectable
groups of close colors. It is thus relatively easy to distinguish images with and without
secret messages. It appears that secure schemes should not manipulate the palette but
rather embed message bits in the image data.
In the next section, we discuss methods that embed message bits as parities of
colors. In Sect. 3, we define the energy of distortions due to message embedding and
introduce the concept of optimal parity assignment that minimizes this energy. An
efficient algorithm for the optimal parity is presented and the proof of optimality is
given. The technique is further extended to multiple pixel embedding. It is shown that
the optimal parity assignment is also optimal for multiple-pixel embedding. In Sect. 4,
we study adaptive steganographic techniques. Two methods are introduced and their
performance is tested on computer generated fractal images. A new technique for
palette images obtained through color quantization and dithering of true-color images
is described in Sect. 5. In this new dithering-while-embedding technique, the image
modifications due to message embedding are diffused through the image in the same
way as the quantization error during dithering. Finally in Sect. 6, we summarize the
new techniques and conclude the paper by outlining future research directions.
2 Message Hiding Using the Parity of Palette Colors
One of the most popular message hiding schemes for palette-based images (GIF files)
has been proposed by Machado [11]. In her method called EZ Stego, the palette is
first sorted by luminance. In the reordered palette, neighboring palette entries are
typically near to each other in the color space, as well. EZ Stego embeds the message
in a binary form into the LSB of randomly chosen pointers to the palette colors. One
can say that this method consists of three steps: parity assignment to palette colors
(ordering the palette), random, key-dependent selection of pixels, and embedding
message into color parities of the selected pixels. Message recovery is simply
achieved by selecting the same pixels and collecting the LSBs of all indices to the
ordered palette. This algorithm is based on the premise that close colors in the
luminance-ordered palette are close in the color space. However, since luminance is a
linear combination of three colors, occasionally colors with similar luminance values
may be relatively far from each other.
To alleviate this problem, Fridrich [6] has proposed to hide message bits into the
parity bits of closest colors1. For the color of each pixel, into which we embed
message bits, the closest colors in the palette are searched till a palette entry is found
with the desired parity bit. The parity of each color could be assigned randomly or
1 Using parity for message embedding has previously been proposed by Petitcolas [1] and
Crandall [5].
50
Jiri Fridrich and Rui Du
simply by calculating R+G+B mod 2. Because the parity bits are randomly
distributed, we will never have to depart from the original color too much. This way,
we avoid the problem of occasionally making large changes in color, which will
certainly contribute to the undetectability of the message. In the absence of a rigorous
security definition for steganography,
the following quantities were accepted as
measures of security:
1. The distance D between the original and the stego-image
D
NM
=
2 =
,
,
ji
1
2
ijd
,
2 = (Rij−Rij')2 + (Gij−Gij')2 + (Bij−Bij')2 for the (i, j)-th pixel of the original
where dij
and the stego-image.
2. The maximal color change
max
,
ji
d
ij
.
Both the average power per pixel and the maximal color change for the new technique
[6] have decreased 4−5 times when compared to the EZ Stego, which is a significant
performance improvement.
In the next section, we investigate the problem of optimal parity assignment for the
palette in order to further improve the scheme described in this section.
3 Optimal Parity Assignment
The parity assignment directly influences the energy of image modifications due to
message embedding. Obviously, if close colors are assigned opposite parities, the
energy of the modifications will be smaller. A natural question to ask is whether it is
possible to further improve the performance by using an optimized palette parity
assignment. For a practical method, which does not have access to the original image,
the palette parity assignment has to be reconstructable from the modified image at the
receiving end.
Let the image palette contain N colors c1, c2, …, cN with parities Pi, Pi ∈{0,1}. The
parity assignment determines an isolation si for the i-th color (si is the distance from
color ci to the closest color with different parity). The colors occur in the original
image with frequencies p1, …, pN, p1+ … + pN = 1. Provided the message carrying
pixels are selected non-adaptively, for a message of length k, approximately kpi pixels
of color ci will contain message bits. The average square of the distance between the
original and the stego-image can be expressed as:
1
2
PkE
1
(
,...,
P
N
)
=
1
2
k
N
=
i
1
sp
i
i
2
.
Secure Steganographic Methods for Palette Images
51
The quantity E does not depend on the message length and will be called the energy
of the parity assignment. The optimization problem is to assign parities P1, …, PN to
colors c1, …, cN so that E is minimal. The following algorithm always finds the
optimal parity assignment that minimizes E:
3.1 Algorithm for Optimal Parity Assignment
1. Calculate the distances between all pairs of colors dij = ci−cj. The distance can
be calculated either in the RGB or the YUV space. Set C = ∅.
2. Order the distances starting from the smallest to the largest, {d} = di(1) j(1) ≤ di(2) j(2)
≤ ….
Iteratively repeat step No. 4 until C contains all N colors.
3.
4. Choose the next distance dkl in the ordered sequence {d} such that either ck ∉C or
cl ∉C. If more than one dkl is the smallest, randomly choose one. If there is no
such dkl this means that C contains all N colors and we are done. If both ck ∉C or
cl ∉C, assign two opposite parities to both k and l. If ck ∉C and cl ∈C, set Pk =
1−Pl. Update C = C ∪{ck}∪{cl}.
It is clear that once a parity of a color is defined, it cannot be changed later by the
algorithm. It is also clear that at the end all colors will have assigned parities. What
needs to be proved is that the parity assignment has the minimal energy E. We point
out that the minimal value of E can occur for more than one parity assignment (see
Fig. 1).
Fig. 1. Example of two different optimal
parity assignments
Proof: Let di denotes the distance from color i to its closest color in the color space.
Obviously, for any parity assignment, P1, …, PN, we have the inequality
PE
1
(
,...,
P
N
)
=
i
N
=
1
2
≥
sp
i
i
i
N
=
1
dp
i
i
2
.
The optimality of the parity found by the algorithm will be proven by showing that di
= si for each i. Let dij be the first occurrence of the index i (color i) in the non-
decreasing sequence {d}. Then the color j must be the closest color to i, because if we
had a different color k, k ≠ j, with dik < dij, the color i would have to occur in {d} prior
to dij. It is true that there might be more than one color j that is closest to i, but in
either case we have di = si, because according to Step 4, we always assign the parities
of i and j to opposite values. This concludes the proof.
52
Jiri Fridrich and Rui Du
Note that the optimal parity assignment does not depend on the frequency of
occurrence of pixels, p1, …, pN. This somewhat contradictory and surprising result
enables us to calculate the optimal parity assignment from the modified image
without accessing the original image. We just need to order the palette before
applying the algorithm (one can use the alphabetical RGB order, for example). If any
random decisions are made during the algorithm run, we need to seed a PRNG with
the same seed, as well. Another possibility would be to agree on a fixed order in the
sequence {d}, the parity assignment for the first pair, and a rule for assigning the
parity when both new nodes ci ∉C and cj ∉C. Either way, the optimal parity can be
utilized for decreasing the energy of modifications in images.
Numerical experiments indicate that when using the optimal parity as opposed to
the parity R+G+B mod 2, the energy E is decreased by 25−35% depending on the
image.
3.2 Multiple-Pixel Embedding
It
is possible to further decrease the energy of modifications due to message
embedding by using clusters of q pixels for one message bit rather than single pixels.
The image is first divided using a PRNG into disjoint clusters of random q pixels and
the message bit is encoded as a parity of the sum of all q pixel parities. This has the
benefit that in order to change the parity of the whole sum one can select a pixel with
the smallest
the energy of
modifications due to message embedding must decrease. The previous method is a
special case of this multiple pixel encoding with q = 1.
isolation among all q pixels. As a consequence,
Below, we show that the optimal parity for this method is the same as for the single
pixel embedding. The energy E of the parity assignment is defined in a similar
manner
)(
qE
=
1
2
N
=
i
1
)(
q
p
i
s
i
,
(q) is the probability that among randomly chosen q pixels in the image the
where pi
(q) does not depend on si, the
one with the smallest isolation is the i-th color. If pi
optimal parity is again only a function of the palette and not of the image. To
(q), we rearrange the colors ci so that their isolations form
calculate the probabilities pi
a non-decreasing sequence. It can easily be shown that
)(
q
p
i
=
N
≥
i
j
)(
q
p
j
q
−
N
>
j
i
)(
q
p
j
q
.
(q) do not depend on the isolations, si, the optimal parity for
Because the probabilities pi
single pixel embedding is also optimal for multiple pixel embedding. The energy E(q)
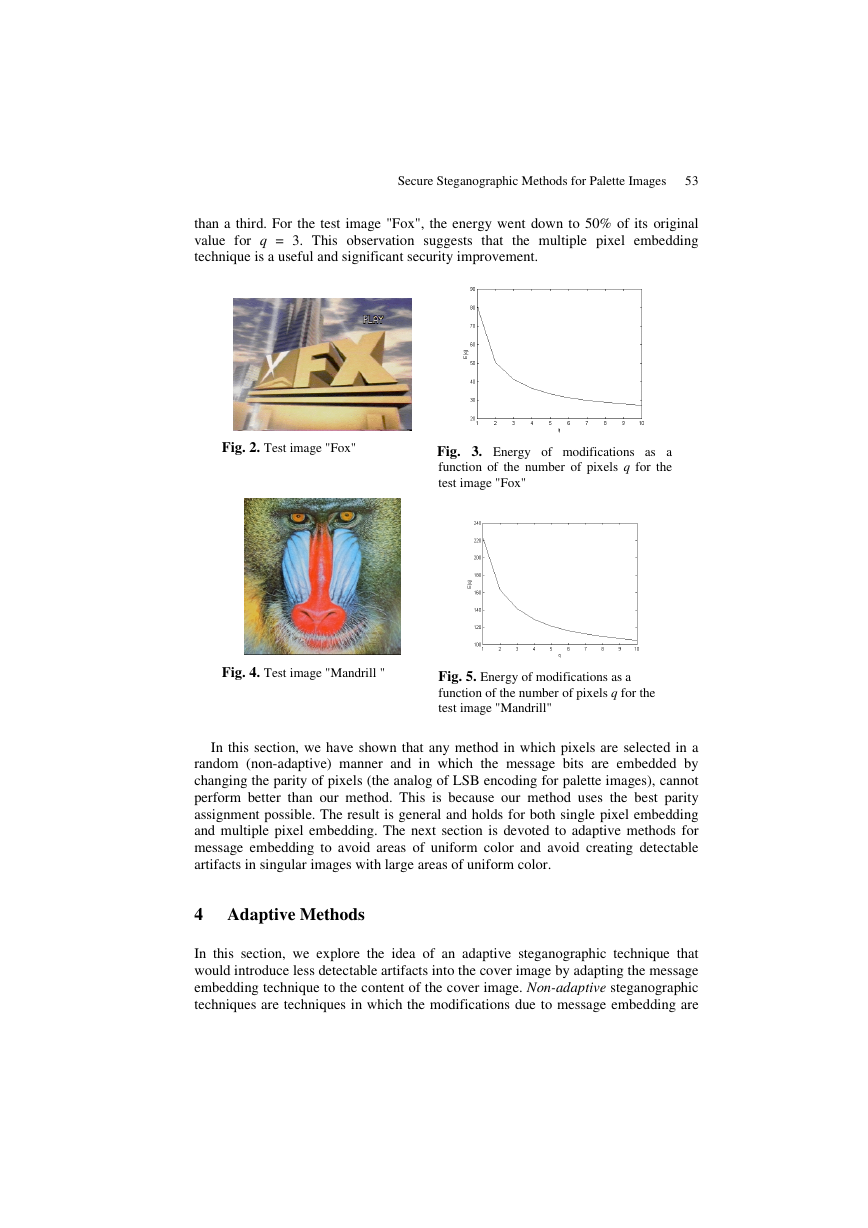
as a function of q is depicted for two test images "Fox" and "Mandrill" in Figs. 2−5.
Observe that even with q = 2, the energy of modifications could decrease by more
Secure Steganographic Methods for Palette Images
53
than a third. For the test image "Fox", the energy went down to 50% of its original
value for q = 3. This observation suggests that
the multiple pixel embedding
technique is a useful and significant security improvement.
Fig. 2. Test image "Fox"
Fig. 3. Energy of modifications as a
function of the number of pixels q for the
test image "Fox"
Fig. 4. Test image "Mandrill "
Fig. 5. Energy of modifications as a
function of the number of pixels q for the
test image "Mandrill"
In this section, we have shown that any method in which pixels are selected in a
random (non-adaptive) manner and in which the message bits are embedded by
changing the parity of pixels (the analog of LSB encoding for palette images), cannot
perform better than our method. This is because our method uses the best parity
assignment possible. The result is general and holds for both single pixel embedding
and multiple pixel embedding. The next section is devoted to adaptive methods for
message embedding to avoid areas of uniform color and avoid creating detectable
artifacts in singular images with large areas of uniform color.
4 Adaptive Methods
In this section, we explore the idea of an adaptive steganographic technique that
would introduce less detectable artifacts into the cover image by adapting the message
embedding technique to the content of the cover image. Non-adaptive steganographic
techniques are techniques in which the modifications due to message embedding are
54
Jiri Fridrich and Rui Du
uncorrelated with image features. Examples are LSB encoding in randomly selected
pixels, message embedding by randomly modulating pixel values or frequency bins in
a fixed band, etc. In adaptive steganography the modifications are correlated with the
image content (features). For steganography, this could mean that the pixels carrying
message bits are selected adaptively and depend on the image. For example, we could
avoid areas of uniform color and select only pixels with large local standard
deviation. This however creates a problem with message recovery if the original
unmodified image is not available. We have to be able to extract the same set of
message carrying pixels at the receiving end from the modified image.
The capacity of adaptive schemes is necessarily image dependent and, in some
cases, it is not even possible to calculate the capacity before the actual embedding
starts. But this is a price we have to pay for increased security. There are several
different ways how a non-adaptive scheme can be turned into an adaptive one. For
example, the message carrying part and the part that determines the pixel selection do
not interact. For example, one can calculate the local standard deviation (STD) from
the 7 most significant bits and embed message bits into the LSB. This approach is
plausible only for high color images and cannot be adopted for palette images.
Method 1. The image is divided into disjoint blocks (for example 3×3 blocks)
completely covering the image. At most one bit will be assigned to each block (either
the LSB of the middle pixel or its parity, or the parity of the whole block, etc.). A
threshold for local STD is selected. A pseudo-random non-intersecting walk over the
blocks is generated from a secret key. If the local STD of a block is above the
threshold AND stays above the threshold after message embedding, we select the
block for message embedding. If the STD falls below the threshold after message
embedding, we make the change anyway but do not include the block for message
embedding, and continue message embedding with the same bit in the next block.
This process will guarantee that at the receiving end it is enough to regenerate the
same random walk over the blocks and read the message bits only from blocks whose
STD is above the threshold. Note that the local standard deviation can be replaced
with a different quantity, such as the number of colors in the block. Actually, our
experiments show that the number of colors works better than the standard deviation
for computer generated low-color images.
The advantage of Method 1 is that any pixel(s) in the block can be modified, which
will generally lead to smaller modifications especially for images with low color
depth. The disadvantage is that it is not possible to say whether or not a message of a
given length will fit into the image before one actually starts the embedding process.
Another disadvantage is somewhat decreased capacity. At most one bit is inserted into
each block, and only blocks with local STD above the threshold are considered for
embedding. It is, however, only natural that more secure schemes will have smaller
capacity, while "greedy" schemes emphasizing the capacity will offer less security. It
will be up to the end user to decide about the priorities.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
