CFD中的动态接触角.pdf

发布时间：2022-06-02 发布人：admin 分类：说明书资料大小：0.71M 资料格式：pdf 举报版权申诉

dj0919-4487002-4744302543287251468.pdf-第1页.png

第1页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第2页.png

第2页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第3页.png

第3页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第4页.png

第4页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第5页.png

第5页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第6页.png

第6页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第7页.png

第7页 / 共8页

dj0919-4487002-4744302543287251468.pdf-第8页.png

第8页 / 共8页

Dynamic contact angles in CFD simulations

Introduction

Capillary filling with static contact angles

Capillary filling with dynamic contact angles

CFD analysis

Phenomenological CFD approach

Summary and conclusions

Acknowledgements

References

Computers & Fluids 38 (2009) 757–764 Contents lists available at ScienceDirect Computers & Fluids j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / c o m p ﬂ u i d Dynamic contact angles in CFD simulations Friedhelm Schönfeld a,*, Steffen Hardt b,1 a Institut für Mikrotechnik Mainz (IMM), Carl-Zeiss-Strasse 18-20, D-55129 Mainz, Germany b Institut für Nano- und Mikroprozesstechnik, Leibniz Universität Hannover, Callinstr. 36, D-30167 Hannover, Germany a r t i c l e i n f o a b s t r a c t Article history: Received 20 April 2007 Received in revised form 4 November 2007 Accepted 27 May 2008 Available online 10 October 2008 The accurate modelling of contact angle properties plays an important role in the simulation of free-sur- face micro ﬂows. Taking capillary ﬁlling as an example, we ﬁrst discuss the analytical solutions of a cor- responding 1D description in certain limits and then derive an approximate analytical expression for the general case with constant contact angle. In case of a dynamic contact angle and contact line friction, the model is beyond an analytical treatment. We show that computational ﬂuid dynamics (CFD) results exhi- bit a pronounced mesh dependence which is partly inherent to the modelling approach since the (non- integrable) viscous stress divergence at the three-phase contact line is commonly neglected in standard CFD simulations (see e.g. Hessel V, Hardt S, Löwe H. Chemical micro process engineering: fundamentals, modelling and reactions. Weinheim: Wiley-VCH; 2004). Moreover, the numerical description of contact angles suffers from artiﬁcial diffusion for the type of volume-of-ﬂuid method used. Introduction of a mac- roscopic slip range in combination with a localised body force close to the contact line turns out to rem- edy both problems. Considering capillary ﬁlling as an example, we show that accurate, mesh independent solutions of ﬂuid dynamic problems involving contact angle dynamics are obtained already on coarse meshes. Ó 2008 Elsevier Ltd. All rights reserved. 1. Introduction Micro ﬂows and their applications have attracted an enhanced interest in the past years. In this context, some of the largest eco- nomical potentials lie in the ﬁelds of chemical process technology [1] and micro total analysis systems (lTAS) [2,3]. lTAS are used for biochemical analysis in medical diagnostics, pharmacological re- search, environmental monitoring and other areas and allow to process small sample amounts in an automated and parallel way. In chemical process technology, microﬂuidics opens the door to new process regimes, safe operation and microﬂuidic reactor com- ponents often allow increased process yields and selectivities. ﬂuid dynamical for macroscopic As far as modelling and simulation of micro ﬂows are con- cerned, the requirements are often different from those character- istic problems. While computational ﬂuid dynamics (CFD) is often confronted with the problem of developing realistic turbulence models for speciﬁc technologically relevant scenarios, micro ﬂows are mostly laminar, so a ﬁrst-principle description can be used to model the ﬂow. How- ever, surface and interface effects become extremely important and have to be included into the models in the most realistic man- ner. Details of the dynamics of the 3-phase contact line of an * Corresponding author. Tel.: +49 (0) 6131 990 411; fax: +49 (0) 6131 990 205. E-mail addresses: schoenf@mnd-umwelttechnik.fh-wiesbaden.de (F. Schönfeld), hardt@nmp.uni-hannover.de (S. Hardt). 1 Tel.: +49 (0) 511 7622 278; fax: +49 (0) 511 7622 167. 0045-7930/$ - see front matter Ó 2008 Elsevier Ltd. All rights reserved. doi:10.1016/j.compﬂuid.2008.05.007 immiscible system of ﬂuids on a solid surface are often neglected in macroscopic simulations. Due to its scaling behaviour, surface tension becomes important pre-dominantly in micro scale geome- tries and is often supposed to be irrelevant in typical macroscopic applications. However, from a fundamental point of view, the physics on the micro scale in close vicinity to the 3-phase contact line, i.e. the region of contact between gas, liquid and solid, dis- plays the most interesting features and has an impact on macro- scopic phenomena. Close to the 3-phase contact line the standard continuum approach breaks down which reﬂects itself in a viscous stress singularity leading to a diverging drag force on the solid surface [4]. This phenomenon was described with the phrase ‘‘not even Herakles could sink a solid” in a paper by Huh and Scriven [4], meaning that the no-slip boundary condition gives rise to inﬁnite forces at the three-phase contact line. Nevertheless, the non-integrable singularity is neglected in most CFD approaches. Relaxing the commonly used no-slip boundary condition removes the singularity [5,6]. This concept of introducing a ﬁnite but micro- scopic slip length at the contact line is feasible within analytical approaches and helps to understand quite universal experimental observations (see e.g. [7]) of dynamic contact angles, i.e. the veloc- ity-dependent enclosed angle between the meniscus tangent at the 3-phase contact line and the wall. For details upon the analytical approaches and on the dependence of the contact line dynamics on the slip length the reader is referred to [8,9] and references therein. Yet, the incorporation of a microscopic length scale that is typically of the order of some ten nanometres into micro ﬂow

758 F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 CFD simulations is not practical for two major reasons. First, typical outer dimensions of microﬂuidic systems are of the order of several millimetres or larger. Thus, the detailed resolution of the region around the contact line requires large numerical efforts. This is true for the slip phenomena discussed above as well as for the micro- scopic ﬂow patterns around a moving contact line. Secondly, the position of a contact line is a priori not known. Therefore, extre- mely high grid resolution has to be provided along the wall bound- ary if no adaptive grid reﬁnement algorithms are used. Since the incorporation of a realistic, microscopic slip condition at the 3-phase contact line is usually not practical in CFD ap- proaches, we present an alternative approach relying on the use of a macroscopic slip range at the 3-phase contact line. By intro- ducing a slip condition within that range the stress singularity is released and the moving meniscus problem is no longer ill-posed. That is reﬂected by the fact that the extraordinarily strong mesh dependence that is found if the no-slip condition is applied is eliminated. Expressed in numerical terms, the strategy we pursue is ex- plained as follows: We consider a problem that does not possess a grid-independent numerical solution if no cut-off scale is intro- duced. The physics of the problem suggests that there is in fact a cut-off scale rendering the problem well-deﬁned that is, however, too small to be incorporated in a reasonable CFD framework. For this reason we use a phenomenological model to describe the problem that does not require the resolution of very small length scales. compares to analytical The speciﬁc aspects of the dynamics of the phase boundary and their implementation into CFD solvers discussed in this arti- cle are of particular importance for simulations of free-surface ﬂow in microﬂuidics. We address the question of how the numer- ically observed wetting behaviour (without any slip length in- cluded) results and whether any discrepancies in the results can be resolved by a phenomenolog- ical approach, relying on a macroscopic range where boundary slip occurs. Generally, several effects such as capillary ﬁlling, con- tact angle hysteresis, dynamic contact angles, instabilities of an advancing wetting front, or dewetting phenomena deserve close investigation. Here the focus is put on a test case of capillary ﬁll- ing, the dynamical behaviour of which is directly related to dy- namic contact angles. The presented approach is also relevant for simulation of industrial processes such as, e.g., air entrain- ment in context with liquid coating. In the following section, the 1D model and certain limits of cap- illary ﬁlling are discussed. This model is taken to benchmark corre- sponding CFD results discussed in the second part where we discuss how the extraordinary strong mesh dependence observed in standard CFD simulations can be removed by introduction of a macroscopic slip range in context with dynamic contact angles and appropriate body forces. 2. Capillary ﬁlling with static contact angles As a classical benchmark system we consider capillary ﬁlling between vertical parallel plates, see Fig. 1. On one hand this sys- tem is simple enough and allows to derive an analytical solution for the ﬁlling height in certain limits. On the other hand the ﬁll- ing dynamics depends sensitively on the contact angle and thus the systems allows to evaluate the CFD scheme for contact angle dynamics developed in the following. Moreover a one-dimen- sional differential equation governing the meniscus dynamics can be derived facilitating analytical solutions in certain limits. For the sake of clarity we start by formulating the Newton’s equation of motion for capillary ﬁlling between vertical parallel plates (cf. e.g. 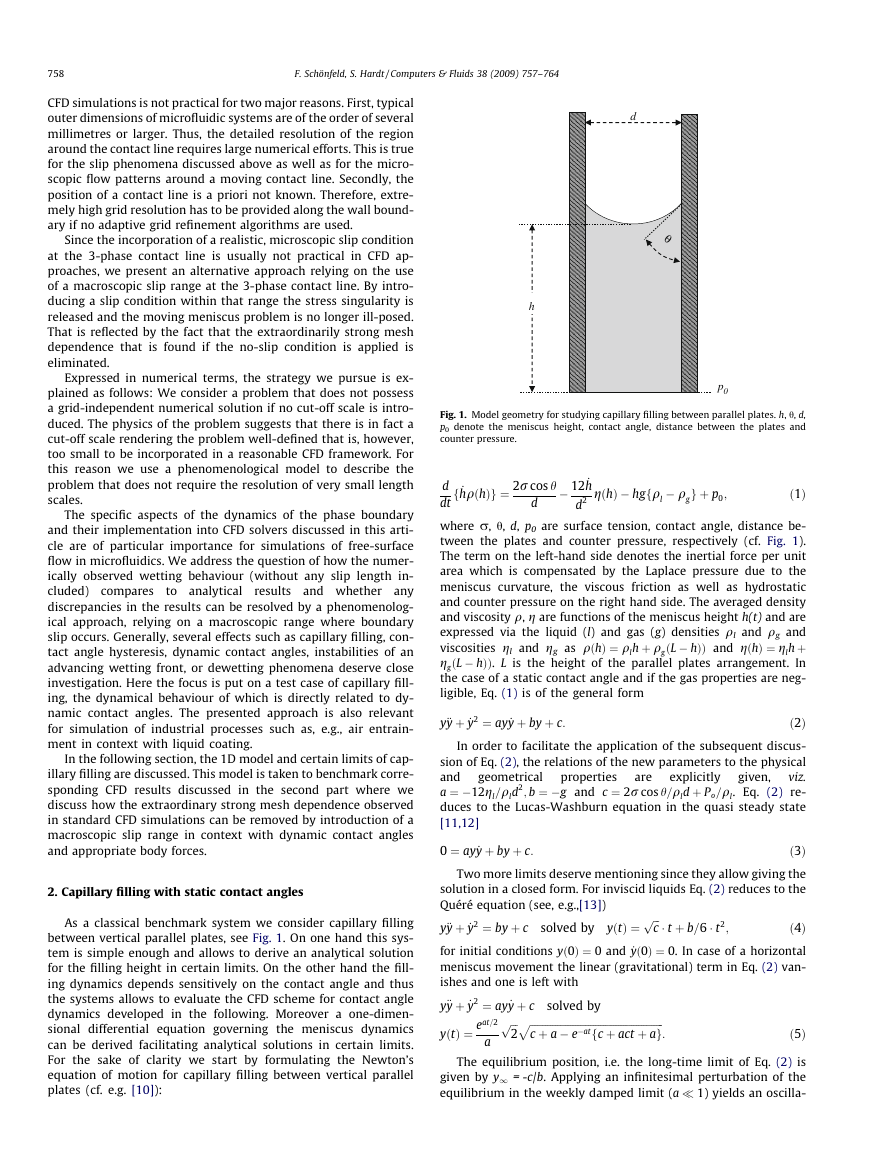[10]): d θ h Fig. 1. Model geometry for studying capillary ﬁlling between parallel plates. h, h, d, p0 denote the meniscus height, contact angle, distance between the plates and counter pressure. p0 12 _h d f _hqðhÞg ¼ 2r cos h d2 gðhÞ hgfql qgg þ p0; d dt where r, h, d, p0 are surface tension, contact angle, distance be- tween the plates and counter pressure, respectively (cf. Fig. 1). The term on the left-hand side denotes the inertial force per unit area which is compensated by the Laplace pressure due to the meniscus curvature, the viscous friction as well as hydrostatic and counter pressure on the right hand side. The averaged density and viscosity q, g are functions of the meniscus height h(t) and are expressed via the liquid (l) and gas (g) densities ql and qg and viscosities gl and gg as qðhÞ ¼ qlh þ qgðL hÞÞ and gðhÞ ¼ glhþ ggðL hÞÞ. L is the height of the parallel plates arrangement. In the case of a static contact angle and if the gas properties are neg- ligible, Eq. (1) is of the general form y€y þ _y2 ¼ ay _y þ by þ c: ð2Þ In order to facilitate the application of the subsequent discus- sion of Eq. (2), the relations of the new parameters to the physical and viz. ; b ¼ g and c ¼ 2r cos h=qld þ Po=ql. Eq. (2) re- a ¼ 12gl=qld2 duces to the Lucas-Washburn equation in the quasi steady state [11,12] 0 ¼ ay _y þ by þ c: solved by yðtÞ ¼ ﬃﬃﬃ p t þ b=6 t2; ð3Þ Two more limits deserve mentioning since they allow giving the solution in a closed form. For inviscid liquids Eq. (2) reduces to the Quéré equation (see, e.g.,[13]) y€y þ _y2 ¼ by þ c ð4Þ for initial conditions yð0Þ ¼ 0 and _yð0Þ ¼ 0. In case of a horizontal meniscus movement the linear (gravitational) term in Eq. (2) van- ishes and one is left with ﬃﬃﬃ p p ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ y€y þ _y2 ¼ ay _y þ c yðtÞ ¼ eat=2 c þ a eatfc þ act þ ag : a geometrical explicitly given, properties are solved by 2 ð1Þ ð5Þ c The equilibrium position, i.e. the long-time limit of Eq. (2) is given by y1 = -c/b. Applying an inﬁnitesimal perturbation of the equilibrium in the weekly damped limit (a 1) yields an oscilla-

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ p b=y1 tory behaviour with a characteristic frequency x0 ¼ [13]. In order to derive an approximate analytical expression for the full dynamics it is helpful to cast Eq. (2) into the form ð€y2Þ ¼ að _y2Þ þ 2by þ 2c: ð6Þ Replacing y2 by z and expanding the square-root term around the equilibrium position y1 = c/b yields an anharmonic-oscillator equation for z(t). Note, the existence of an equilibrium position im- plies non-vanishing gravity, i.e. b < 0. €z ¼ a_z þ 2b ﬃﬃﬃﬃﬃﬃ ﬃﬃﬃﬃﬃﬃ p þ z z1 p þ Oðz2Þ z1 z1 þ 2c: ð7Þ 2 By numerical integration of Eq. (7), the linear term in z(t) is found to be at least an order of magnitude larger than the quadratic term for the set of parameters given below. This motivates us to neglect the anharmonic terms. In this case the solution has the general form of a damped oscillatory motion around the equilib- rium position. Neglecting further the frequency shift due to the damping the solution of Eq. 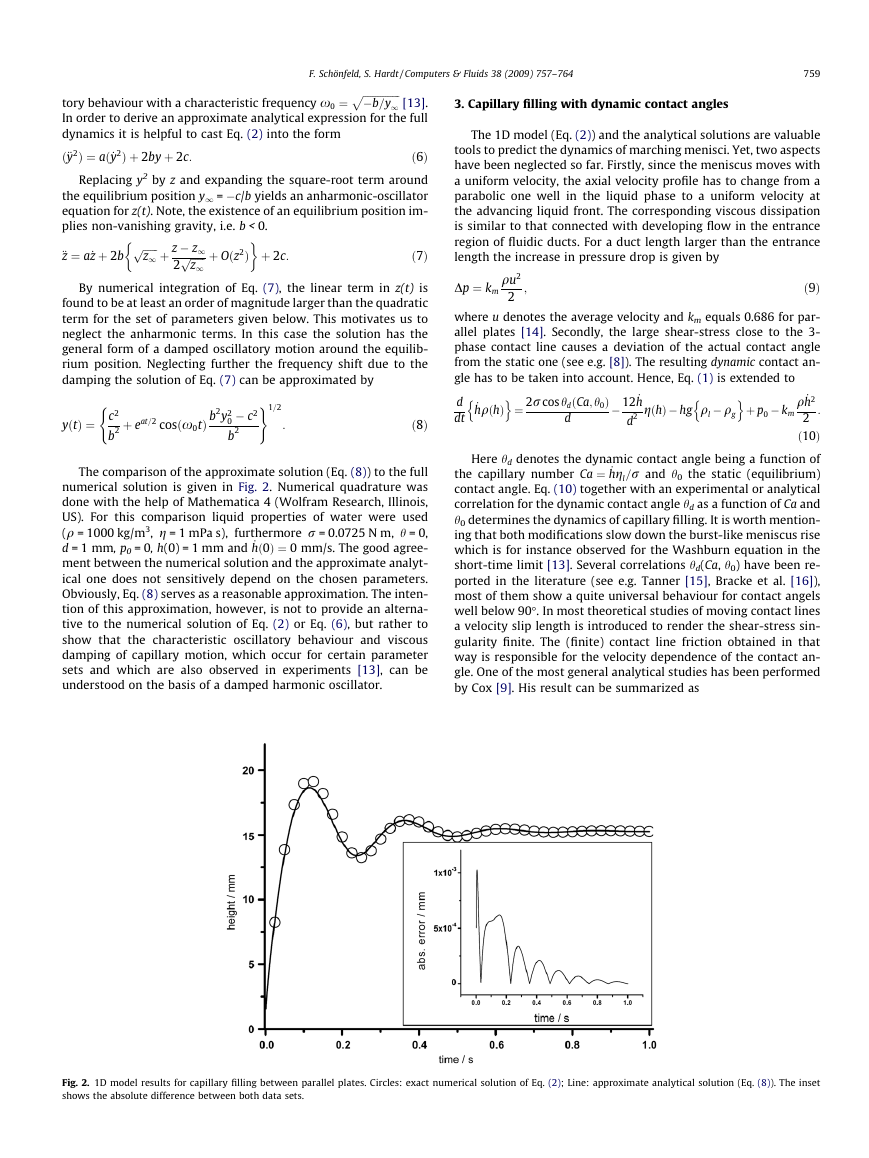(7) can be approximated by ( b2 þ eat=2 cosðx0tÞ b2y2 yðtÞ ¼ c2 0 c2 b2 ) 1=2 : ð8Þ The comparison of the approximate solution (Eq. (8)) to the full numerical solution is given in Fig. 2. Numerical quadrature was done with the help of Mathematica 4 (Wolfram Research, Illinois, US). For this comparison liquid properties of water were used (q = 1000 kg/m3, g = 1 mPa s), furthermore r = 0.0725 N m, h = 0, d = 1 mm, p0 = 0, h(0) = 1 mm and _hð0Þ ¼ 0 mm/s. The good agree- ment between the numerical solution and the approximate analyt- ical one does not sensitively depend on the chosen parameters. Obviously, Eq. (8) serves as a reasonable approximation. The inten- tion of this approximation, however, is not to provide an alterna- tive to the numerical solution of Eq. (2) or Eq. (6), but rather to show that the characteristic oscillatory behaviour and viscous damping of capillary motion, which occur for certain parameter sets and which are also observed in experiments [13], can be understood on the basis of a damped harmonic oscillator. F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 759 3. Capillary ﬁlling with dynamic contact angles The 1D model (Eq. (2)) and the analytical solutions are valuable tools to predict the dynamics of marching menisci. Yet, two aspects have been neglected so far. Firstly, since the meniscus moves with a uniform velocity, the axial velocity proﬁle has to change from a parabolic one well in the liquid phase to a uniform velocity at the advancing liquid front. The corresponding viscous dissipation is similar to that connected with developing ﬂow in the entrance region of ﬂuidic ducts. For a duct length larger than the entrance length the increase in pressure drop is given by Dp ¼ km ð9Þ qu2 2 ; n o n o _hqðhÞ where u denotes the average velocity and km equals 0.686 for par- allel plates [14]. Secondly, the large shear-stress close to the 3- phase contact line causes a deviation of the actual contact angle from the static one (see e.g. [8]). The resulting dynamic contact an- gle has to be taken into account. Hence, Eq. (1) is extended to d d dt þ p0 km ¼ 2r cos hdðCa; h0Þ 12 _h d2 gðhÞ hg ql qg q _h2 2 : ð10Þ Here hd denotes the dynamic contact angle being a function of the capillary number Ca ¼ _hgl=r and h0 the static (equilibrium) contact angle. Eq. (10) together with an experimental or analytical correlation for the dynamic contact angle hd as a function of Ca and h0 determines the dynamics of capillary ﬁlling. It is worth mention- ing that both modiﬁcations slow down the burst-like meniscus rise which is for instance observed for the Washburn equation in the short-time limit [13]. Several correlations hd(Ca, h0) have been re- ported in the literature (see e.g. Tanner [15], Bracke et al. [16]), most of them show a quite universal behaviour for contact angels well below 90°. In most theoretical studies of moving contact lines a velocity slip length is introduced to render the shear-stress sin- gularity ﬁnite. The (ﬁnite) contact line friction obtained in that way is responsible for the velocity dependence of the contact an- gle. One of the most general analytical studies has been performed by Cox [9]. His result can be summarized as Fig. 2. 1D model results for capillary ﬁlling between parallel plates. Circles: exact numerical solution of Eq. (2); Line: approximate analytical solution (Eq. (8)). The inset shows the absolute difference between both data sets.

760 F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 gðhdÞ ¼ gðh0Þ þ Ca lnðl1 ð11Þ s Þ; where ls denotes the dimensionless length of the slip region and the ﬃﬃﬃﬃﬃﬃ function g is given in [9]. In the following, the somewhat simpler empirical correlation derived by Bracke et al. (1989) is used p cosðhdÞ ¼ cosðh0Þ 2½1 þ cosðh0Þ Ca : ð12Þ It has to be stressed, however, that the CFD approach discussed subsequently allows to implement other correlations as well and does not depend on the particular choice of hd(Ca, h0). Inserting Eq. (12) in Eq. (10) yields a highly non-linear differential equation of the form ﬃﬃﬃ p _y ; the newly introduced parameter and y€y ¼ ay _y þ by þ c0 þ d1 _y2 þ d2 ð13Þ ﬃﬃﬃﬃﬃﬃﬃﬃ are deﬁned as where d2 ¼ 4½1 þ cos h0 c0 ¼ 2r cos h0=qld þ P0=ql; d1 ¼ km=2 1, p rgl =qld. The square-root term in Eq. (13) represents the friction of the contact line motion. Interestingly, the square-root depen- dence of the contact line friction was also derived independently of any dynamic contact angle correlation by comparing numerical solutions of the Navier–Stokes equations to experimental data [17]. Since straightforward analytical approaches fail, Eq. (13) is solved numerically (Mathematica 4, Wolfram Research, Illinois, US). The solution of the 1D model is taken as a benchmark for the CFD results discussed below. Already in the analysis of the 1D ap- proach it will turn out that the dynamic behaviour is extremely sensitive to details of the dynamic contact angle, thus facilitating the evaluation of numerical accuracy. Such an indirect monitoring of the contact angle is much more accurate than the direct quanti- ﬁcation by numerical determination of the slope of the interface at the wall. 3.1. CFD analysis We start our CFD analysis by simulating capillary rise with a static contact angle as it has been investigated by Quinte et al. [18]. Many CFD solvers, as CFX4, allow for explicit application of contact angles as boundary conditions which translates to deﬁning the tangential and normal component of the normalized volume- fraction function at the boundary nodes (see. e.g. [19]). In this con- text the term ‘‘static contact angle” means that a velocity-indepen- dent contact angle has been applied as boundary condition to the model, while friction forces in the vicinity of the contact line may still alter the contact angle dynamically. The test case is worth studying because up to date most CFD simulations of marching contact lines are based on such a description. Hence, it gives valu- able information about the performance of standard CFD tools. The CFD results as well as the numerical solution of the 1D model are displayed in Fig. 3. Again, liquid properties of water as given above were chosen. The static contact angle was set to 55°, the plate dis- tance to 1 mm and the initial height of the meniscus to 2 mm. In order to lower the equilibrium position and to reduce the extent of the computational domain a counter pressure of 49.95 Pa was applied (total length L = 5 mm, cf. Fig. 1). The dashed lines in Fig. 3 denote the CFD results based on the solution of the incom- pressible Navier–Stokes equations on Cartesian meshes of 250, 1000, 4000, 16,000 and 64,000 cells in two dimensions (cf. Fig. 4). For pressure–velocity coupling, the SIMPLEC algorithm [20] was used. The free-surface ﬂow was modelled using the vol- ume-of-ﬂuid (VOF) method (see, e.g., [21]) which describes the time evolution of the separated phases on a ﬁxed computational grid by a convection equation for a volume-fraction function. For discretization of the volume-fraction equation a ﬂux-limited high- er-order upwind scheme [22] was used. 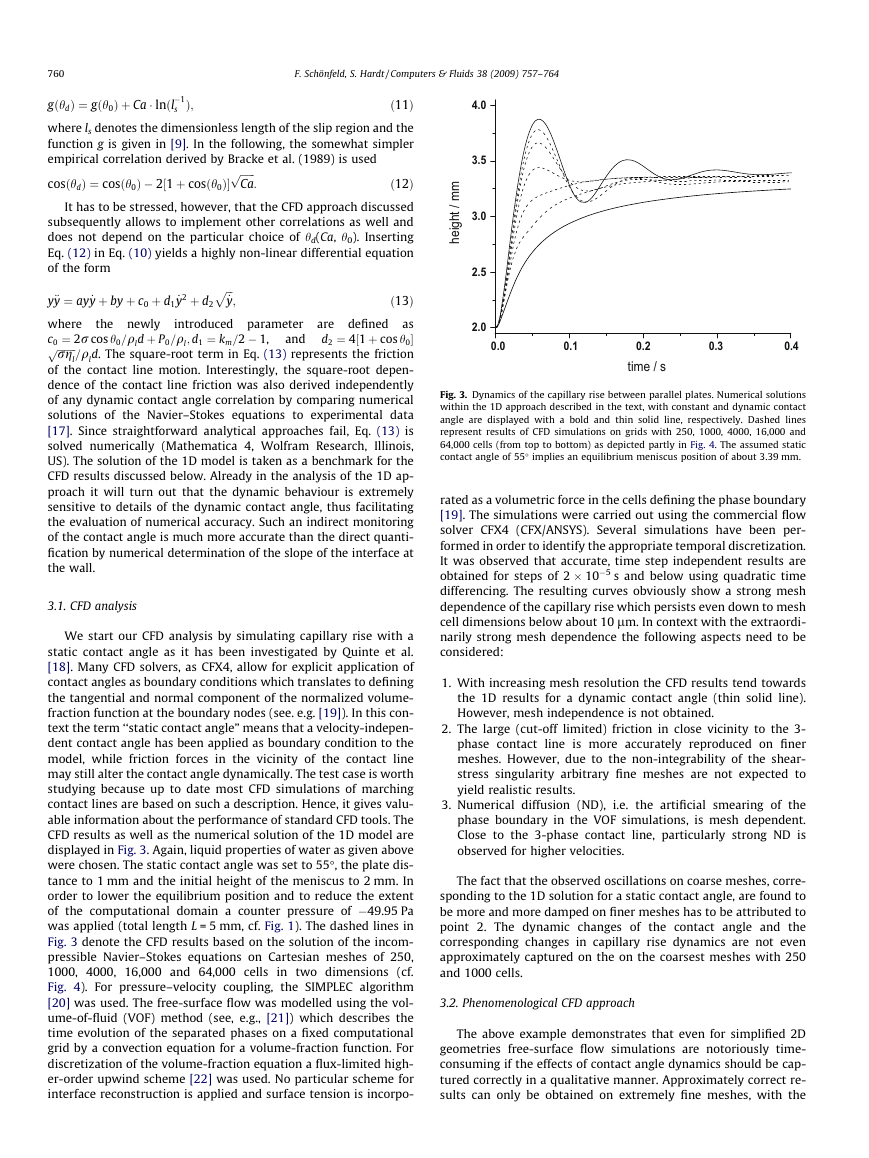No particular scheme for interface reconstruction is applied and surface tension is incorpo- m m / t h g e h i 4.0 3.5 3.0 2.5 2.0 0.0 0.1 0.2 0.3 0.4 time / s Fig. 3. Dynamics of the capillary rise between parallel plates. Numerical solutions within the 1D approach described in the text, with constant and dynamic contact angle are displayed with a bold and thin solid line, respectively. Dashed lines represent results of CFD simulations on grids with 250, 1000, 4000, 16,000 and 64,000 cells (from top to bottom) as depicted partly in Fig. 4. The assumed static contact angle of 55° implies an equilibrium meniscus position of about 3.39 mm. rated as a volumetric force in the cells deﬁning the phase boundary [19]. The simulations were carried out using the commercial ﬂow solver CFX4 (CFX/ANSYS). Several simulations have been per- formed in order to identify the appropriate temporal discretization. It was observed that accurate, time step independent results are obtained for steps of 2 105 s and below using quadratic time differencing. The resulting curves obviously show a strong mesh dependence of the capillary rise which persists even down to mesh cell dimensions below about 10 lm. In context with the extraordi- narily strong mesh dependence the following aspects need to be considered: 1. With increasing mesh resolution the CFD results tend towards the 1D results for a dynamic contact angle (thin solid line). However, mesh independence is not obtained. 2. The large (cut-off limited) friction in close vicinity to the 3- phase contact line is more accurately reproduced on ﬁner meshes. However, due to the non-integrability of the shear- stress singularity arbitrary ﬁne meshes are not expected to yield realistic results. 3. Numerical diffusion (ND), i.e. the artiﬁcial smearing of the phase boundary in the VOF simulations, is mesh dependent. Close to the 3-phase contact line, particularly strong ND is observed for higher velocities. The fact that the observed oscillations on coarse meshes, corre- sponding to the 1D solution for a static contact angle, are found to be more and more damped on ﬁner meshes has to be attributed to point 2. The dynamic changes of the contact angle and the corresponding changes in capillary rise dynamics are not even approximately captured on the on the coarsest meshes with 250 and 1000 cells. 3.2. Phenomenological CFD approach The above example demonstrates that even for simpliﬁed 2D geometries free-surface ﬂow simulations are notoriously time- consuming if the effects of contact angle dynamics should be cap- tured correctly in a qualitative manner. Approximately correct re- sults can only be obtained on extremely ﬁne meshes, with the

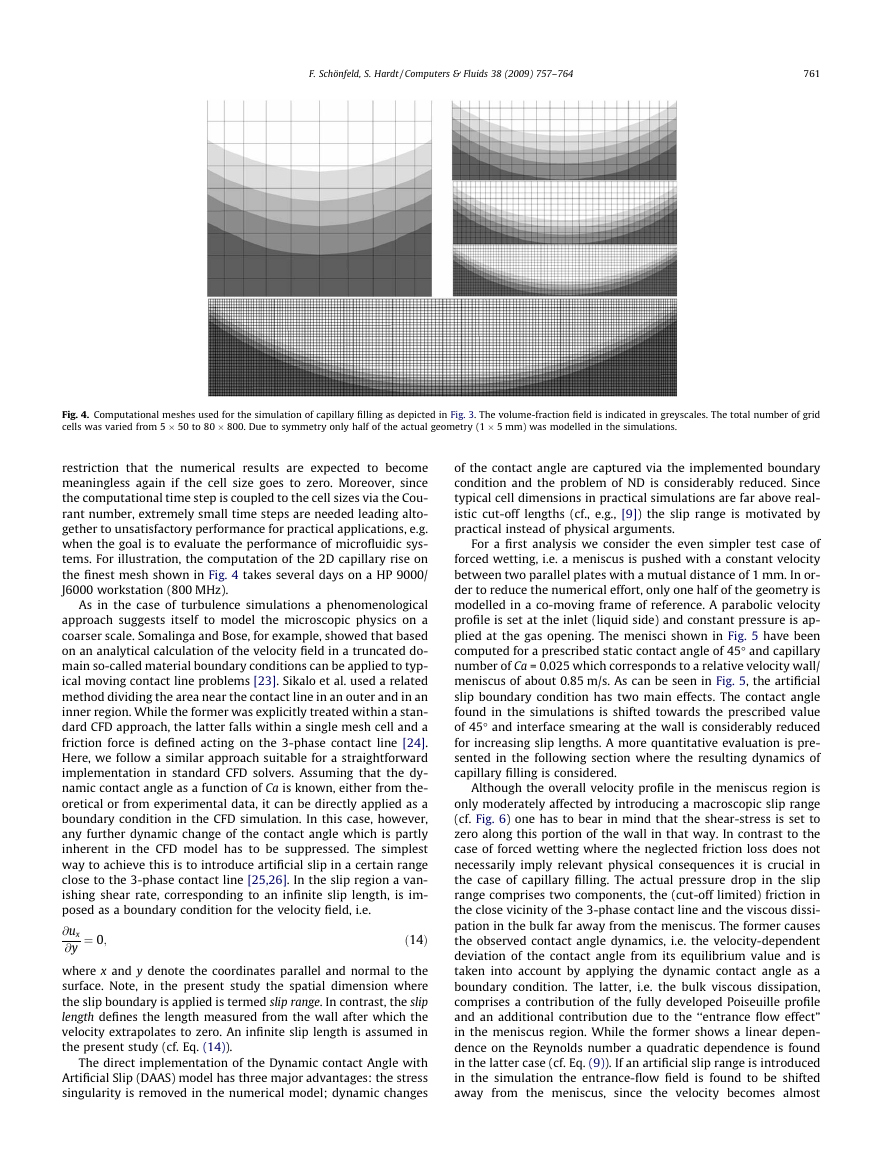
F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 761 Fig. 4. Computational meshes used for the simulation of capillary ﬁlling as depicted in Fig. 3. The volume-fraction ﬁeld is indicated in greyscales. The total number of grid cells was varied from 5 50 to 80 800. Due to symmetry only half of the actual geometry (1 5 mm) was modelled in the simulations. restriction that the numerical results are expected to become meaningless again if the cell size goes to zero. Moreover, since the computational time step is coupled to the cell sizes via the Cou- rant number, extremely small time steps are needed leading alto- gether to unsatisfactory performance for practical applications, e.g. when the goal is to evaluate the performance of microﬂuidic sys- tems. For illustration, the computation of the 2D capillary rise on the ﬁnest mesh shown in Fig. 4 takes several days on a HP 9000/ J6000 workstation (800 MHz). As in the case of turbulence simulations a phenomenological approach suggests itself to model the microscopic physics on a coarser scale. Somalinga and Bose, for example, showed that based on an analytical calculation of the velocity ﬁeld in a truncated do- main so-called material boundary conditions can be applied to typ- ical moving contact line problems [23]. Sikalo et al. used a related method dividing the area near the contact line in an outer and in an inner region. While the former was explicitly treated within a stan- dard CFD approach, the latter falls within a single mesh cell and a friction force is deﬁned acting on the 3-phase contact line [24]. Here, we follow a similar approach suitable for a straightforward implementation in standard CFD solvers. Assuming that the dy- namic contact angle as a function of Ca is known, either from the- oretical or from experimental data, it can be directly applied as a boundary condition in the CFD simulation. In this case, however, any further dynamic change of the contact angle which is partly inherent in the CFD model has to be suppressed. The simplest way to achieve this is to introduce artiﬁcial slip in a certain range close to the 3-phase contact line [25,26]. In the slip region a van- ishing shear rate, corresponding to an inﬁnite slip length, is im- posed as a boundary condition for the velocity ﬁeld, i.e. @ux @y ð14Þ ¼ 0; where x and y denote the coordinates parallel and normal to the surface. Note, in the present study the spatial dimension where the slip boundary is applied is termed slip range. In contrast, the slip length deﬁnes the length measured from the wall after which the velocity extrapolates to zero. An inﬁnite slip length is assumed in the present study (cf. Eq. (14)). The direct implementation of the Dynamic contact Angle with Artiﬁcial Slip (DAAS) model has three major advantages: the stress singularity is removed in the numerical model; dynamic changes of the contact angle are captured via the implemented boundary condition and the problem of ND is considerably reduced. Since typical cell dimensions in practical simulations are far above real- istic cut-off lengths (cf., e.g., [9]) the slip range is motivated by practical instead of physical arguments. For a ﬁrst analysis we consider the even simpler test case of forced wetting, i.e. a meniscus is pushed with a constant velocity between two parallel plates with a mutual distance of 1 mm. In or- der to reduce the numerical effort, only one half of the geometry is modelled in a co-moving frame of reference. A parabolic velocity proﬁle is set at the inlet (liquid side) and constant pressure is ap- plied at the gas opening. The menisci shown in Fig. 5 have been computed for a prescribed static contact angle of 45° and capillary number of Ca = 0.025 which corresponds to a relative velocity wall/ meniscus of about 0.85 m/s. As can be seen in Fig. 5, the artiﬁcial slip boundary condition has two main effects. The contact angle found in the simulations is shifted towards the prescribed value of 45° and interface smearing at the wall is considerably reduced for increasing slip lengths. A more quantitative evaluation is pre- sented in the following section where the resulting dynamics of capillary ﬁlling is considered. Although the overall velocity proﬁle in the meniscus region is only moderately affected by introducing a macroscopic slip range (cf. Fig. 6) one has to bear in mind that the shear-stress is set to zero along this portion of the wall in that way. In contrast to the case of forced wetting where the neglected friction loss does not necessarily imply relevant physical consequences it is crucial in the case of capillary ﬁlling. The actual pressure drop in the slip range comprises two components, the (cut-off limited) friction in the close vicinity of the 3-phase contact line and the viscous dissi- pation in the bulk far away from the meniscus. The former causes the observed contact angle dynamics, i.e. the velocity-dependent deviation of the contact angle from its equilibrium value and is taken into account by applying the dynamic contact angle as a boundary condition. The latter, i.e. the bulk viscous dissipation, comprises a contribution of the fully developed Poiseuille proﬁle and an additional contribution due to the ‘‘entrance ﬂow effect” in the meniscus region. While the former shows a linear depen- dence on the Reynolds number a quadratic dependence is found in the latter case (cf. Eq. (9)). If an artiﬁcial slip range is introduced in the simulation the entrance-ﬂow ﬁeld is found to be shifted away from the meniscus, since the velocity becomes almost

762 F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 Fig. 5. Computed menisci for forced wetting with varying slip ranges 0, 50, 200, 250 lm (black arrows on the right hand side of each geometry), Ca = 0.025, h = 45°. Within the menisci dark grey (white) denotes a liquid volume-fraction of one (zero). The approximate contact angles are depicted on the left-hand sides. Fig. 6. Pressure distribution and velocity ﬁeld in the liquid phase close to the marching meniscus. The grey levels denote pressure difference in steps of 20 Pa. The slip range is indicated by bold vertical arrows. The dashed rectangle marks the area where the body force is applied (cf. Eq. (15)). constant over the channel cross section already at the position where the slip range starts. Thus, by introduction of a slip range the additional pressure drop due to the entrance-ﬂow is still main- tained, but the part of the Poiseuille pressure drop over the exten- sion of that region has been neglected. This is compensated by introducing a body force, depending linearly on the average ﬂow velocity, in the momentum equation. More precise, we introduce an additional force density in the axial component of the Navier– Stokes equations for the liquid phase qux þ ðu rÞqux ¼ @ @x @ @t where ux denotes the axial velocity component, q the density of the (incompressible) liquid, g its viscosity, p the pressure and B the p þ gr2ux þ B; ð15Þ additional body force density, which is assumed to be proportional to the average axial velocity U. We have found that details of the distribution of the body force over the slip region are of minor importance as long as it is assured that the shape of the gas–liquid interface is not altered. Here, a homogeneous distribution perpen- dicular to the ﬂow direction was used as indicated by the dashed rectangle in Fig. 6. In the corresponding cells a body force density B = rU was applied. However, the pre-factor r is a priori not known and may be regarded as a ﬁt parameter. In the absence of reliable experimental data we use the numerical 1D solution as a bench- mark case in order to demonstrate the usefulness of the DAAS ap- proach. For further evaluation we reinvestigate the test case of capillary ﬁlling with a static and with a velocity-dependent contact angle (cf. Fig. 3), however, this time with much faster dynamics in

F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 763 order to highlight the capability of the proposed approach. To this end the ﬂuid density is reduced to ql = 10 kg/m3 and the counter pressure (p0) is set to zero, furthermore gl is set to 2 mPas. It should be noted that due to the faster dynamics the problem becomes much harder for the numerical analysis. Corresponding CFD results together with the numerical 1D solution are shown in Fig. 7. The so- lid curves denote the 1D solutions with a static (upper curve) and a dynamic (lower curve) contact angle. The dashed (long dashed) curves denote CFD solutions on various grids with the default no- slip boundary condition for the static (dynamic) case. Again CFD re- sults are found to be inadequate since no mesh independent solu- tion can be extrapolated. 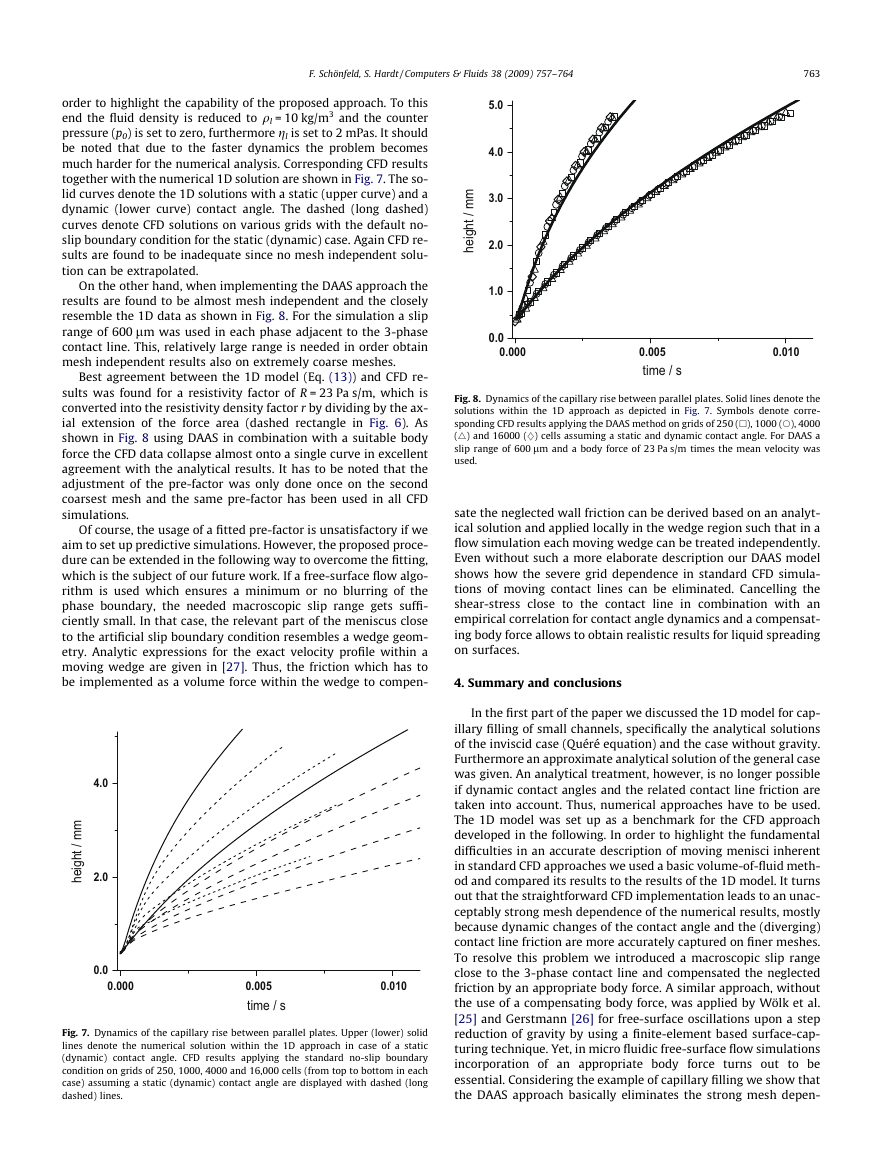On the other hand, when implementing the DAAS approach the results are found to be almost mesh independent and the closely resemble the 1D data as shown in Fig. 8. For the simulation a slip range of 600 lm was used in each phase adjacent to the 3-phase contact line. This, relatively large range is needed in order obtain mesh independent results also on extremely coarse meshes. Best agreement between the 1D model (Eq. (13)) and CFD re- sults was found for a resistivity factor of R = 23 Pa s/m, which is converted into the resistivity density factor r by dividing by the ax- ial extension of the force area (dashed rectangle in Fig. 6). As shown in Fig. 8 using DAAS in combination with a suitable body force the CFD data collapse almost onto a single curve in excellent agreement with the analytical results. It has to be noted that the adjustment of the pre-factor was only done once on the second coarsest mesh and the same pre-factor has been used in all CFD simulations. Of course, the usage of a ﬁtted pre-factor is unsatisfactory if we aim to set up predictive simulations. However, the proposed proce- dure can be extended in the following way to overcome the ﬁtting, which is the subject of our future work. If a free-surface ﬂow algo- rithm is used which ensures a minimum or no blurring of the phase boundary, the needed macroscopic slip range gets sufﬁ- ciently small. In that case, the relevant part of the meniscus close to the artiﬁcial slip boundary condition resembles a wedge geom- etry. Analytic expressions for the exact velocity proﬁle within a moving wedge are given in [27]. Thus, the friction which has to be implemented as a volume force within the wedge to compen- 4.0 2.0 m m / t h g e h i 0.0 0.000 0.005 0.010 time / s Fig. 7. Dynamics of the capillary rise between parallel plates. Upper (lower) solid lines denote the numerical solution within the 1D approach in case of a static (dynamic) contact angle. CFD results applying the standard no-slip boundary condition on grids of 250, 1000, 4000 and 16,000 cells (from top to bottom in each case) assuming a static (dynamic) contact angle are displayed with dashed (long dashed) lines. 5.0 4.0 3.0 2.0 1.0 m m / t h g e h i 0.0 0.000 0.005 0.010 time / s Fig. 8. Dynamics of the capillary rise between parallel plates. Solid lines denote the solutions within the 1D approach as depicted in Fig. 7. Symbols denote corre- sponding CFD results applying the DAAS method on grids of 250 (h), 1000 (s), 4000 (4) and 16000 (}) cells assuming a static and dynamic contact angle. For DAAS a slip range of 600 lm and a body force of 23 Pa s/m times the mean velocity was used. sate the neglected wall friction can be derived based on an analyt- ical solution and applied locally in the wedge region such that in a ﬂow simulation each moving wedge can be treated independently. Even without such a more elaborate description our DAAS model shows how the severe grid dependence in standard CFD simula- tions of moving contact lines can be eliminated. Cancelling the shear-stress close to the contact line in combination with an empirical correlation for contact angle dynamics and a compensat- ing body force allows to obtain realistic results for liquid spreading on surfaces. 4. Summary and conclusions In the ﬁrst part of the paper we discussed the 1D model for cap- illary ﬁlling of small channels, speciﬁcally the analytical solutions of the inviscid case (Quéré equation) and the case without gravity. Furthermore an approximate analytical solution of the general case was given. An analytical treatment, however, is no longer possible if dynamic contact angles and the related contact line friction are taken into account. Thus, numerical approaches have to be used. The 1D model was set up as a benchmark for the CFD approach developed in the following. In order to highlight the fundamental difﬁculties in an accurate description of moving menisci inherent in standard CFD approaches we used a basic volume-of-ﬂuid meth- od and compared its results to the results of the 1D model. It turns out that the straightforward CFD implementation leads to an unac- ceptably strong mesh dependence of the numerical results, mostly because dynamic changes of the contact angle and the (diverging) contact line friction are more accurately captured on ﬁner meshes. To resolve this problem we introduced a macroscopic slip range close to the 3-phase contact line and compensated the neglected friction by an appropriate body force. A similar approach, without the use of a compensating body force, was applied by Wölk et al. [25] and Gerstmann [26] for free-surface oscillations upon a step reduction of gravity by using a ﬁnite-element based surface-cap- turing technique. Yet, in micro ﬂuidic free-surface ﬂow simulations incorporation of an appropriate body force turns out to be essential. Considering the example of capillary ﬁlling we show that the DAAS approach basically eliminates the strong mesh depen-

764 F. Schönfeld, S. Hardt / Computers & Fluids 38 (2009) 757–764 dence of CFD results for moving contact line problems. In other words, the numerical results achieved on the coarsest mesh (250 cells) are almost indistinguishable from those computed on a ﬁner mesh with 64 times as much cells, while all of these data agree well with the results of the 1D model. We believe that the pre- sented approach shows a route to performing free-surface ﬂow CFD computations in micro ﬂuidics with an accurate description of contact angle dynamics and a reasonable use of CPU resources. Moreover, the presented DAAS approach does not rely on the type of numerical method for free-surface ﬂow and can also be applied in the context of, e.g., PLIC-VOF schemes [28], level-set schemes [29] or interface-tracking techniques (see, e.g., [21]). Clearly, more work needs to be done to corroborate the above statements for arbitrary geometries and applications. The imple- mentation of DAAS for 3D problems is in principle analogous to the 2D example discussed above, since locally the pre-dominant motion is 1D, perpendicular to the contact line. However, it re- quires an efﬁcient identiﬁcation of the slip area close to the 3- phase contact line which could be done based on the gradient of the volume-fraction function. Moreover, in 3D and for complex geometries the deﬁnition of a suitable body force compensating for the neglected viscous friction will be less straightforward. A possibility to obtain this force without a ﬁtting procedure would be to resort to analytical solutions for the velocity ﬁeld in a moving wedge, such as given by Dussan [27]. Acknowledgements The work has been supported by the DFG-Forschergruppe FOR 516/1 and by the German Ministry of Research and Education, Grant No. 16SV1355. References [1] Hessel V, Hardt S, Löwe H. Chemical micro process engineering: fundamentals, modelling and reactions. Weinheim: Wiley-VCH; 2004. [2] Reyes DR, Iossiﬁdis D, Auroux PA, Manz A. Micro total analysis systems. 1. Introduction, theory, and technology. Anal Chem 2002;74:2623–36. [3] Auroux PA, Iossiﬁdis D, Reyes DR, Manz A. Micro total analysis systems. 2. Analytical standard operations and applications. Anal Chem 2002;74:2637–52. [4] Huh C, Scriven LE. Hydrodynamic model of steady movement of a solid/liquid/ ﬂuid contact line. J Colloid Interface Sci 1971;35:85–101. [5] Hocking LM. A moving ﬂuid interface. Part 2. The removal of the force singularity by a slip ﬂow. J Fluid Mech 1977;79:209–29. [6] Huh C, Mason SG. The steady movement of a liquid meniscus in a capillary tube. J Fluid Mech 1977;81:401–19. [7] Kistler S. Hydrodynamics of wetting. In: Wettability S, Berg JC, editors. New York: Dekker; 1993. [8] De Gennes PG. Wetting: statics and dynamics. Rev Mod Phys 1985;57:827–63. [9] Cox RG. The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous ﬂow. J Fluid Mech 1986;168:169–94. [10] Levine S, Reed P, Watson EJ, Neale G. A theory of the rate of rise of a liquid in a capillary. In: Kerker M, editor. Colloid and interface science, vol. III. New York: Academic Press; 1976. p. 403–19. [11] Lucas R. Über das Zeitgesetz des Kapillaren Aufstiegs von Flussigkeiten. Kolloid Z 1918;23:15–21. [12] Washburn E. The dynamics of capillary ﬂow. Phys Rev 1921;17:273–83. [13] Zhmud BV, Tiberg F, Hallstensson K. Dynamics of capillary rise. J Colloid Interface Sci 2000;228:263–9. [14] Lundgren TS, Sparrow EM, Starr JB. Pressure drop due to the entrance region in ducts of arbitrary cross section. J Basic Eng 1964;86:620–6. [15] Tanner LH. The spreading of silicone oil drops on horizontal surfaces. J Phys D: Appl Phys 1979;12:1473–84. [16] Bracke M, de Voeght F, Joos P. The kinetics of wetting: the dynamic contact angle. Prog Colloid Polym Sci 1989;79:142–9. [17] Zhou MY, Sheng P. Dynamics of immiscible-ﬂuid displacement in a capillary tube. Phys Rev Lett 1990;64:882–5. [18] Quinte A, Halstenberg S, Eggert H, Peters RP, Schön C. Mikrosystemtechnische Realisierung von medizinischen Teststreifen, Proceedings 8. Workshop, Methoden und Werkzeuge zum Entwurf von Mikrosystemen‘‘, Berlin, December 2–3, 1999;13–22. [19] Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension. J Comp Phys 1992;100:335–54. [20] Van Doormal JP, Raithby GD. Enhancements of the SIMPLE method for predicting incompressible ﬂuid ﬂows. Numer Heat Transfer 1984;7: 147–63. [21] Ferziger JH, Peric M. Computational methods for ﬂuid dynamics. 3rd ed. Heidelberg: Springer; 2002. [22] Van Leer B. Towards the ultimate conservative difference scheme. A second order Sequel to Godunov’s Method. J Comp Phys 1979;32:101–36. [23] Somalinga S, Bose A. Numerical investigation of boundary conditions for moving contact line problems. Phys Fluids 2000;12:499–510. [24] Sikalo S, Wilhelm H-D, Roisman IV, Jakirlic S, Tropea C. Dynamic contact angle of spreading droplets: Experiments and simulations. Phys Fluids 2005;17: 0621031–13. [25] Wölk G, Dreyer M, Rath HJ, Weislogel MM. Damped oscillations of liquid/gas surface upon step reduction in gravity. J Spacecraft Rockets 1997;34(1): 110–7. [26] Gerstmann zur J. Numerische Untersuchungen freier Flüssigkeitsoberﬂächen. Ph.D. Thesis, Fortschritt-Berichte VDI 7, 2004; 464, ISBN 3-18-346407-1. Schwingung [27] Dussan EB. The moving contact line: the slip boundary condition. J. Fluid Mech 1976;77:665–84. [28] Rider WJ, Kothe DB. Reconstructing volume tracking. J Comp Phys 1998;141:112–52. [29] Osher S, Sethian JA. Fronts propagating with curvature-dependent speed: J Comp Phys formulations. algorithms based on Hamilton–Jacobi 1988;79:12–49.

分享到：

赞收藏

资料库

CFD中的动态接触角.pdf

相关推荐

行业

热门标签

最新资料