第1页 / 共83页
第2页 / 共83页
第3页 / 共83页
第4页 / 共83页
第5页 / 共83页
第6页 / 共83页
第7页 / 共83页
第8页 / 共83页
动态规划经典教程及题目（含代码）.docx
动态规划的很经典的教程
1. 动态规划基本概
1.1动态规划三要素
1.2动态规划的适用范围
1.3动态规划解决问题的一般思路
2. 动态规划分类讨论
2.1一维状态
2.1.1下降/非降子序列问题
例题1 拦截导弹 (missile.pas/c/cpp) 来源：NOIP1999(提高组) 第
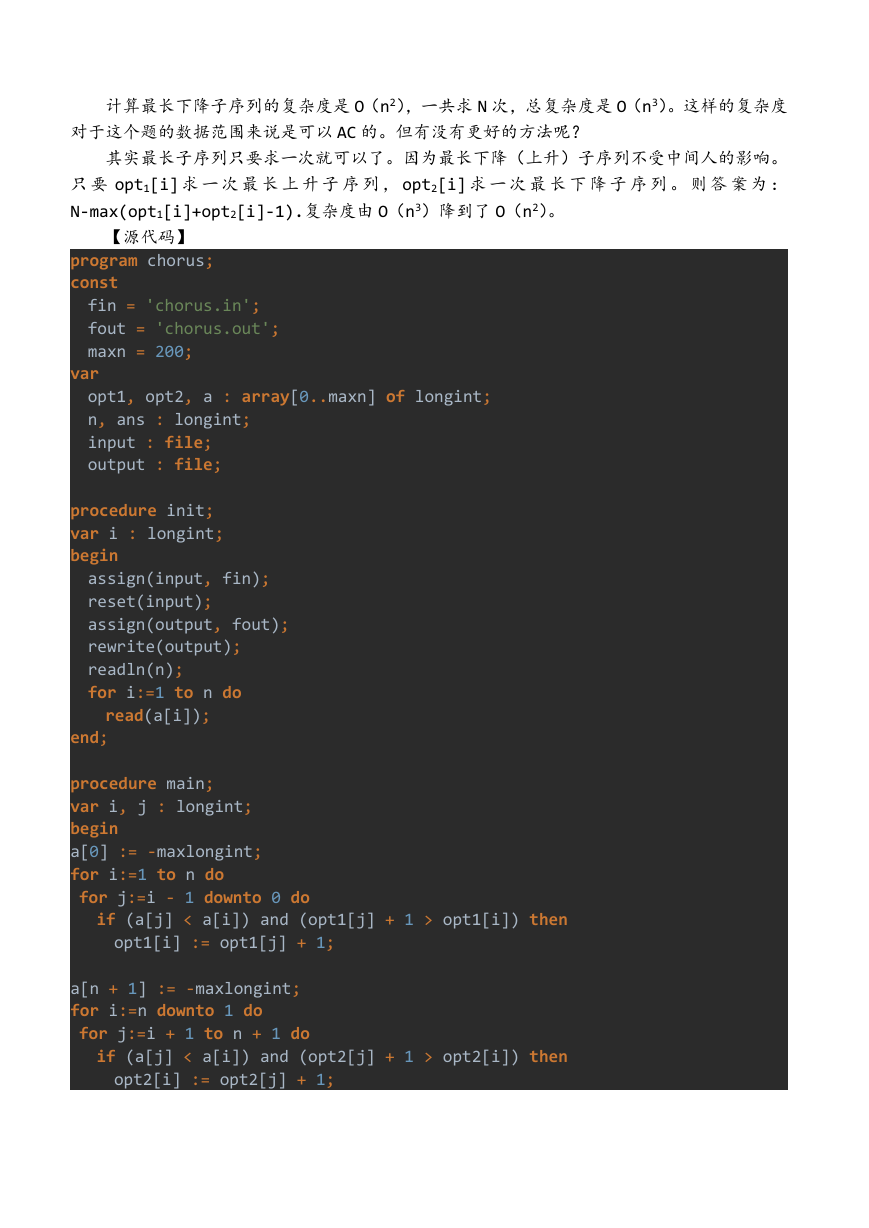
例题二 合唱队形 (chorus.pas/c/cpp) 来源：NOIP2004(提高组) 第一
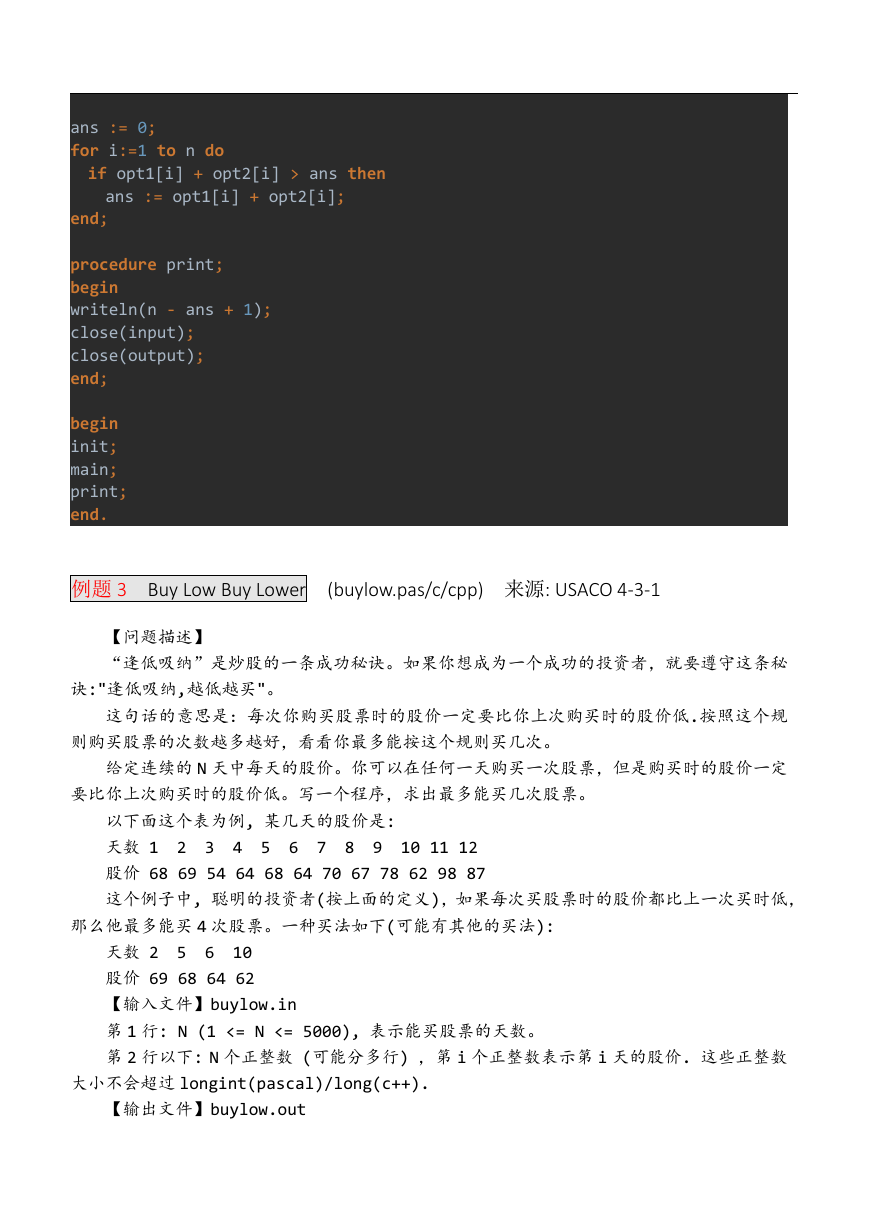
例题3 Buy Low Buy Lower (buylow.pas/c/cpp) 来源: US
例题4 船 (ships.pas/c/cpp) 来源：《奥赛经典》（提高篇）
2.1.2背包问题
例题5 装箱问题 (pack.pas/c/cpp) 来源：NOIP2001(普及组) 第四题
例题6 砝码称重 来源：NOIP1996（提高组） 第四题
例题7 积木城堡 来源：vijos P1059
例题8 采药 (medic.pas/c/cpp) 来源：NOIP2005（普及组） 第三题
例题9 开心的金明 来源：NOIP2006（普及组）第二题
例题10 金明的预算方案 (budget.pas/c/cpp) 来源：NOIP2006 第二题
例题11 Money Systems (money.pas/c/cpp) 来源：USACO 2
例题12 新年趣事之打牌 来源： vijos P1071
2.1.3其它问题
例题13 挖地雷问题 (P3.pas/c/cpp) 来源：NOIP1996（提高组）第三题（有
2.2 二维状态
2.2.1数塔问题
例题14 数塔问题 (numtri.pas/c/cpp) 来源：IOI94
例题15 Henry捡钱 (money.pas/c/cpp) 来源：Dream Team邀请赛
2.2.2街道问题
例题16 街道问题 (way.pas/c/cpp) 来源：《奥赛经典》（提高篇）
2.2.3最长公共子序列问题
例题17 最长公共子序列 (lcs.pas/c/cpp) 来源：《全国青少年信息学奥林匹克联赛
例题18 回文词 (palin.pas/c/cpp) 来源：IOI 2000
例题19 调整队形 (queue.pas/c/cpp) 来源：TJU P1006
2.2.4 背包问题的拓展
例题20 找啊找啊找GF (gf.pas/c/cpp) 来源：MM群2007七夕模拟赛（RQN
例题21 多多看DVD（加强版） (watchdvd.pas/c/cpp) 来源：本人原创
2.2.5石子合并问题
例题22 石子合并 (stone.pas/c/cpp) 来源：某年NOI（去巴蜀交）
例题23 能量项链 (energy.pas/c/cpp) 来源NOIP2006（提高组）
例题24 统计单词个数 (.pas/c/cpp) 来源：NOIP2001（提高组）
2.2.6其他问题
例题25 花店橱窗设计 (flower.pas/c/cpp) 来源：IOI或巴蜀评测系统
例题26 Divisibility 来源：ZJU2042
2.3 多维状态和动态规划的优化
2.3.1 矩阵问题
例题27 盖房子 来源：VIJOS P1057
2.3.2多进程动态规划
例题28 方格取数 (fgqs.pas/c/cpp) 来源：NOIP2000(提高组)
2.4 树型动态规划
例题29 加分二叉树 (binary.pas/c/cpp) 来源：NOIP2003（提高组）
例题30 A Binary Apple Tree 苹果二叉树 来源：URAL P1018
例题31 选课 来源：VIJOS P1180
动态规划的很经典的教程
引言：本人在做过一些题目后对 DP 有些感想，就写了这个总结。
1. 动态规划基本概
1.1 动态规划三要素
阶段，状态，决策。
他们的概念到处都是，我就不多说了，我只说说我对他们的理解：
如果把动态规划的求解过程看成一个工厂的生产线，阶段就是生产某个商品的不同的环节，
状态就是工件当前的形态，决策就是对工件的操作。显然不同阶段是对产品的一个前面各个状
态的小结，有一个个的小结构成了最终的整个生产线。每个状态间又有关联（下一个状态是由
上一个状态做了某个决策后产生的）。
下面举个例子：
要生产一批雪糕，在这个过程中要分好多环节：购买牛奶，对牛奶提纯处理，放入工厂加
工，加工后的商品要包装，包装后就去销售……，这样每个环节就可以看做是一个阶段；产品
在不同的时候有不同的状态，刚开始时只是白白的牛奶，进入生产后做成了各种造型，从冷冻
库拿出来后就变成雪糕（由液态变成固态=_=||）。每个形态就是一个状态，那从液态变成固态
经过了冰冻这一操作，这个操作就是一个决策。
一个状态经过一个决策变成了另外一个状态，这个过程就是状态转移，用来描述状态转移
的方程就是状态转移方程。
经过这个例子相信大家对动态规划有所了解了吧。
下面在说说我对动态规划的另外一个理解：
用图论知识理解动态规划：把动态规划中的状态抽象成一个点，在有直接关联的状态间连
一条有向边，状态转移的代价就是边上的权。这样就形成了一个有向无环图 AOE 网（为什么无
环呢？往下看）。对这个图进行拓扑排序，删除一个边后同时出现入度为 0 的状态在同一阶段。
这样对图求最优路径就是动态规划问题的求解。
1.2 动态规划的适用范围
动态规划用于解决多阶段决策最优化问题，但是不是所有的最优化问题都可以用动态规划
解答呢？
一般在题目中出现求最优解的问题就要考虑动态规划了，但是否可以用还要满足两个条件：
1. 最优子结构（最优化原理）
2. 无后效性
最优化原理在下面的最短路径问题中有详细的解答；
什么是无后效性呢？
就是说在状态 i 求解时用到状态 j 而状态 j 就解有用到状态 k…..状态 N。
而求状态 N 时有用到了状态 i 这样求解状态的过程形成了环就没法用动态规划解答了，这
也是上面用图论理解动态规划中形成的图无环的原因。
也就是说当前状态是前面状态的完美总结，现在与过去无关。。。
当然，有时换一个划分状态或阶段的方法就满足无后效性了，这样的问题仍然可以用动态
规划解。
1.3 动态规划解决问题的一般思路
拿到多阶段决策最优化问题后，第一步要判断这个问题是否可以用动态规划解决，如果不能就要考虑搜
索或贪心了。当确定问题可以用动态规划后，就要用下面介绍的方法解决问题了：
（1）模型匹配法：
最先考虑的就是这个方法了。挖掘问题的本质，如果发现问题是自己熟悉的某个基本的模
型，就直接套用，但要小心其中的一些小的变动，现在考题一般都是基本模型的变形套用时要
小心条件，三思而后行。这些基本模型在先面的分类中将一一介绍。
（2）三要素法
仔细分析问题尝试着确定动态规划的三要素，不同问题的确定方向不同：
a.先确定阶段的问题：数塔问题，和走路问题（详见解题报告）
b.先确定状态的问题：大多数都是先确定状态的。
c.先确定决策的问题：背包问题。（详见解题报告）
一般都是先从比较明显的地方入手，至于怎么知道哪个明显就是经验问题了，多做题就会
发现。
（3）寻找规律法：
这个方法很简单，耐心推几组数据后，看他们的规律，总结规律间的共性，有点贪心的意
思。
（4）边界条件法
找到问题的边界条件，然后考虑边界条件与它的邻接状态之间的关系。这个方法也很起效。
（5）放宽约束和增加约束
这个思想是在陈启锋的论文里看到的，具体内容就是给问题增加一些条件或删除一些条件
使问题变的清晰。
2. 动态规划分类讨论
这里用状态维数对动态规划进行了分类。
2.1 一维状态
2.1.1 下降/非降子序列问题
问题描述：{挖掘题目的本质，一但抽象成这样的描述就可以用这个方法解}
在一个无序的序列 a1,a2,a3,a4…an 里，找到一个最长的序列满足：ai < = aj <= ak <=…
<= am，且 I < j< k < …< m（最长非降子序列）或 ai>aj>ak>…>am,且 i>j>k…>m（最长下
降子序列）。
问题分析：
如果前 i - 1 个数中用到 ak (ak > ai 或 ak <= ai)构成了一个的最长的序列加上第 i 个
数 ai 就是前 i 个数中用到 ai 的最长的序列了。那么求用到 ak 构成的最长的序列有要求前 k-1
个数中……。
a. 从上面的分析可以看出这样划分问题满足最优子结构。
b. 那满足无后效性么？显然对于第 i 个数只考虑前 i-1 个数，显然满足无后效性，可以用动
态规划解。
分析到这里，动态规划的三要素就不难得出了：
如果按照序列编号划分阶段，设计一个状态 opt[i]表示前 i 个数中用到第 i 个数所构成
的最优解。那么决策就是在前 i-1 个状态中找到最大的 opt[j]使得 aj > ai(或 aj <= ai)，
opt[j]+1 就是 opt[i]的值；用方程表示为：（我习惯了这种写法，但不是状态转移方程的标
准写法。）
opt[i] = max(opt[j])+1 (0<=jai) {最长下降子序列}
实现求解最长下降子序列的部分代码：
for j:=0 to i-1 do
if ( a[j] > a[i]) and (opt[j]+1 > opt[i]) then
1. opt[0]:=maxsize; {maxsize 为 maxlongint 或 -maxlongint}
2. for i:=1 to n do
3.
4.
5.
6. ans:=-maxlongint;
7. for i:=1 to n do
8.
9.
opt[i]:=opt[j]+1;
if opt[i]>ans then
ans:=opt[i]; {ans 为最终解}
复杂度：从上面的实现不难看出时间复杂度为 O（n2），空间复杂度 O（n）；
例题 1 拦截导弹 (missile.pas/c/cpp) 来源：NOIP1999(提高组) 第一题
【问题描述】
某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个
缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高
度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此
有可能不能拦截所有的导弹。
输入导弹依次飞来的高度（雷达给出的高度数据是不大于 30000 的正整数），计算这套系
统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
【输入文件】missile.in
单独一行列出导弹依次飞来的高度。
【输出文件】missile.out
两行，分别是最多能拦截的导弹数，要拦截所有导弹最少要配备的系统数
【输入样例】
389 207 155 300 299 170 158 65
【输出样例】
6
2
【问题分析】
有经验的选手不难看出这是一个求最长非升子序列问题，显然标准算法是动态规划。
以导弹依次飞来的顺序为阶段。设计状态 opt[i]表示前 i 个导弹中，如果拦截了导弹 i，
则可以拦截最多能拦截到的导弹的个数。
状态转移方程：
opt[i]=max(opt[j])+1 (h[j]>=h[i],0=
inc( n );
read( a[n] );
until
seekeof;
assign( input, fin );
reset( input );
assign( output, fout );
rewrite( output );
n:= 0;
repeat
14. output:file;
15. begin
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26. end;
27.
28. procedure main;
29. var i,j:longint;
30. begin fillchar(opt, sizeof(opt), 0);
31. a[0]:=maxlongint;
32.
33. for i:=1 to n do
34.
35.
36.
37. anslen:= 0;
38. for i : = 1 to n do
39.
40.
41. fillchar(opt, sizeof(opt), 0);
42. a[0]:=-maxlongint;
43.
44. for i:=1 to n do
45.
46.
47.
48. anstime:= 0;
49. for i : = 1 to n do
50.
51.
52. end;
53.
54. procedure print;
if opt[i] > anstime then
anstime : = opt[i];
if opt[i] > anslen then
anslen : = opt[i];
for j:=i-1 downto 0 do
for j:=i-1 downto 0 do
if (a[j]>=a[i]) and (opt[j]+1>opt[i]) then //第一问
opt[i]:=opt[j]+1;
if (a[j]opt[i]) then
//第二问
opt[i]:=opt[j]+1;
55. begin writeln( anslen );
56. writeln( anstime );
57. close( input );
58. close( output );
59. end;
60.
61. begin init;
62. main;
63. print;
64. end.
例题二 合唱队形 (chorus.pas/c/cpp) 来源：NOIP2004(提高组) 第一题
【问题描述】
N 位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的 K 位同学排成合
唱队形。
合唱队形是指这样的一种队形：设 K 位同学从左到右依次编号为 1，2…，K，他们的身高
分别为 T1，T2，…，TK，则他们的身高满足 T1<...Ti+1>…>TK (1<=i<=K)。
你的任务是，已知所有 N 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同
学排成合唱队形。
【输入文件】
输入文件：chorus.in
它的第一行是一个整数 N(2<=N<=100)，表示同学的总人数。第二行有 n 个整数，用空格
分隔，第 i 个整数 Ti (130<=Ti<=230)是第 i 位同学的身高(厘米)。
【输出文件】
输出文件：chorus.out
它只包括一行，这一行只包含一个整数，就是最少需要几位同学出列。
【样例输入】
8
186 186 150 200 160 130 197 220
【样例输出】
4
【数据规模】
对于 50％的数据，保证有 n<=20；
对于全部的数据，保证有 n<=100。
【问题分析】
出列人数最少，也就是说留的人最多，也就是序列最长。
这样分析就是典型的最长下降子序列问题。只要枚举每一个人站中间时可以的到的最优解。
显然它就等于，包括他在内向左求最长上升子序列，向右求最长下降子序列。
我们看一下复杂度：
计算最长下降子序列的复杂度是 O（n2），一共求 N 次，总复杂度是 O（n3）。这样的复杂度
对于这个题的数据范围来说是可以 AC 的。但有没有更好的方法呢？
其实最长子序列只要求一次就可以了。因为最长下降（上升）子序列不受中间人的影响。
只 要 opt1[i] 求 一 次 最 长 上 升 子 序 列 ， opt2[i] 求 一 次 最 长 下 降 子 序 列 。 则 答 案 为 ：
N-max(opt1[i]+opt2[i]-1).复杂度由 O（n3）降到了 O（n2）。
【源代码】
program chorus;
const
fin = 'chorus.in';
fout = 'chorus.out';
maxn = 200;
var
opt1, opt2, a : array[0..maxn] of longint;
n, ans : longint;
input : file;
output : file;
procedure init;
var i : longint;
begin
assign(input, fin);
reset(input);
assign(output, fout);
rewrite(output);
readln(n);
for i:=1 to n do
read(a[i]);
end;
procedure main;
var i, j : longint;
begin
a[0] := -maxlongint;
for i:=1 to n do
for j:=i - 1 downto 0 do
if (a[j] < a[i]) and (opt1[j] + 1 > opt1[i]) then
opt1[i] := opt1[j] + 1;
a[n + 1] := -maxlongint;
for i:=n downto 1 do
for j:=i + 1 to n + 1 do
if (a[j] < a[i]) and (opt2[j] + 1 > opt2[i]) then
opt2[i] := opt2[j] + 1;
ans := 0;
for i:=1 to n do
end;
if opt1[i] + opt2[i] > ans then
ans := opt1[i] + opt2[i];
procedure print;
begin
writeln(n - ans + 1);
close(input);
close(output);
end;
begin
init;
main;
print;
end.
例题 3 Buy Low Buy Lower
(buylow.pas/c/cpp) 来源: USACO 4-3-1
【问题描述】
“逢低吸纳”是炒股的一条成功秘诀。如果你想成为一个成功的投资者，就要遵守这条秘
诀:"逢低吸纳,越低越买"。
这句话的意思是：每次你购买股票时的股价一定要比你上次购买时的股价低.按照这个规
则购买股票的次数越多越好，看看你最多能按这个规则买几次。
给定连续的 N 天中每天的股价。你可以在任何一天购买一次股票，但是购买时的股价一定
要比你上次购买时的股价低。写一个程序，求出最多能买几次股票。
以下面这个表为例, 某几天的股价是:
天数 1 2 3 4 5 6 7 8 9 10 11 12
股价 68 69 54 64 68 64 70 67 78 62 98 87
这个例子中, 聪明的投资者(按上面的定义)，如果每次买股票时的股价都比上一次买时低，
那么他最多能买 4 次股票。一种买法如下(可能有其他的买法):
天数 2 5 6 10
股价 69 68 64 62
【输入文件】buylow.in
第 1 行: N (1 <= N <= 5000), 表示能买股票的天数。
第 2 行以下: N 个正整数 (可能分多行) ，第 i 个正整数表示第 i 天的股价. 这些正整数
大小不会超过 longint(pascal)/long(c++).
【输出文件】buylow.out
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
