2015年北京大兴中考数学真题及答案.doc-资料库

第1页 / 共19页

第2页 / 共19页

第3页 / 共19页

第4页 / 共19页

第5页 / 共19页

第6页 / 共19页

第7页 / 共19页

第8页 / 共19页

2015 年北京大兴中考数学真题及答案一、选择题（本题共 30 分，每小题 3 分）下面各题均有四个选项，其中只有一个是符合题意的 1．截止到 2015 年 6 月 1 日，北京市已建成 34 个地下调蓄设施，蓄水能力达到 1 40 000 立方平米。将 1 40 000 用科学记数法表示应为( ) A．14×104 B．1.4×105 C．1.4×106 D．0.14×106 2．实数 a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是( ) A．a B．b C．c D．d 3．一个不透明的盒子中装有 3 个红球，2 个黄球和 1 个绿球，这些球除了颜色外无其他差 1 2 别，从中随机摸出一个小球，恰好是黄球的概率为( 1 3 ) A． B． C． 1 6 D． 2 3 4．剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为( ) A B C D 5．如图，直线 l1，l2，l3 交于一点，直线 l4∥l1，若∠1=124°，∠2=88°，则∠3 的度数为( ) A．26° B．36° C．46° D．56° （第 5 题图）（第 6 题图）（第 7 题图） 6．如图，公路 AC，BC 互相垂直，公路 AB 的中点 M 与点 C 被湖隔开，若测得 AM 的长为 1.2km，则 M，C 两点间的距离为（） A．0.5km B．0.6km C．0.9km D．1.2km 7．某市 6 月份日平均气温统计如图所示，则在日平均气温这组数据中，众数和中位数分别是（） A．21，21 B．21，21.5 C．21，22 D．22，22

8．下图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图。若这个坐标系分别以正东、正北方向为 x轴、y轴的正方向。表示太和门的点坐标为（0，-1），表示九龙壁的点的坐标为（4，1），则表示下列宫殿的点的坐标正确的是（） A．景仁宫（4，2） B．养心殿（-2，3） C．保和殿（1，0） D．武英殿（-3.5，-4） 9．一家游泳馆的游泳收费标准为 30 元/次，若购买会员年卡，可享受如下优惠：会员年卡类型办卡费用（元）每次游泳收费（元） A 类 B 类 C 类 50 200 400 25 20 15 例如，购买 A 类会员卡，一年内游泳 20 次，消费 50+25×20=550 元，若一年内在该游泳馆游泳的次数介于 45~55 次之间，则最省钱的方式为（） A．购买 A 类会员年卡 B．购买 B 类会员年卡 C．购买 C 类会员年卡 D．不购买会员年卡 10．一个寻宝游戏的寻宝通道如图 1 所示，通道由在同一平面内的 AB，BC，CA，OA，OB， OC 组成。为记录寻宝者的进行路线，在 BC 的中点 M 处放置了一台定位仪器，设寻宝者行进的时间为 x，寻宝者与定位仪器之间的距离为 y，若寻宝者匀速行进，且表示 y与 x的函数关系的图象大致如图 2 所示，则寻宝者的行进路线可能为（） A．A→O→B B．B→A→C C．B→O→C D．C→B→O

二、填填空题（本题共 18 分，每小题 3 分） 11．分解因式：5x2-10x2=5x=_________． 12．如图是由射线 AB，BC，CD，DE，组成的平面图形，则∠1+∠2+∠3+∠4+∠5=_____． 13．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架。它的代数成就主要包括开放术、正负术和方程术。其中，方程术是《九章算术》最高的数学成就。《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两。问牛、羊各直金几何？”译文：“假设有 5 头牛、2 只羊，值金 10 两；2 头牛、5 只羊，值金 8 两。问每头牛、每只羊各值金多少两” 设每头牛值金 x，每只羊各值金 y两，可列方程组为_____________． 14．关于 x 的一元二次方程 ax2+bx+ 1 =0 有两个相等的实数根，写出一组满足条件的实数 a， 4 b的值：a=______，b=______． 15．北京市 2009-2014 年轨道交通日均客运量统计如图所示。根据统计图中提供信息，预估 2015 年北京市轨道交通日均客运量约________万人次，你的预估理由是 ________________________．

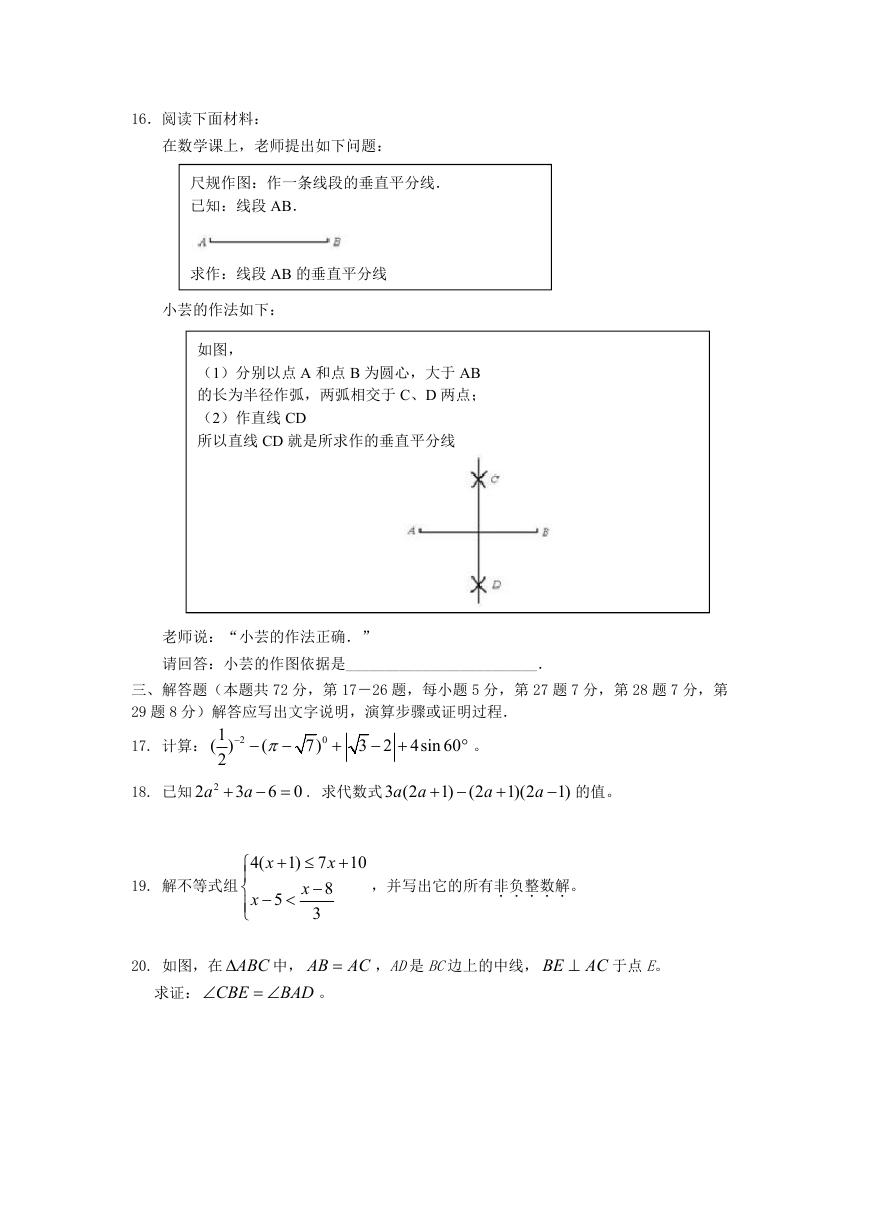
16．阅读下面材料：在数学课上，老师提出如下问题：尺规作图：作一条线段的垂直平分线．已知：线段 AB．求作：线段 AB 的垂直平分线小芸的作法如下：如图，（1）分别以点 A 和点 B 为圆心，大于 AB 的长为半径作弧，两弧相交于 C、D 两点；（2）作直线 CD 所以直线 CD 就是所求作的垂直平分线老师说：“小芸的作法正确．” 请回答：小芸的作图依据是_________________________．三、解答题（本题共 72 分，第 17－26 题，每小题 5 分，第 27 题 7 分，第 28 题 7 分，第 29 题 8 分）解答应写出文字说明，演算步骤或证明过程． ) 17. 计算： 1( 2 18. 已知 22 3 a a 2    ( 0 7)  3 2   4sin 60  。   . 求代数式 3 (2 a a 6 0 1)   (2 a  1)(2 a 1)  的值。 19. 解不等式组     4( x 1) 7 x   8 x  3 x   5  10 ，并写出它的所有非负整数解．．．．．。 20. 如图，在 ABC   求证： CBE 中， AB AC BAD  。，AD是 BC边上的中线， BE AC 于点 E。

21. 为解决“最后一公里”的交通接驳问题，北京市投放了大量公租自行车供市民使用。到 2013 年底，全市已有公租自行车 25000 辆，租赁点 600 个，预计到 2015 年底，全市将有公租自行车 50000 辆，并且平均每个租赁点的公租自行车数量是 2013 年底平均每个租赁点的公租自行车数量的 1.2 倍。预计到 2015 年底，全市将有租赁点多少个？ 22. 在 ABCD BF。中，过点 D作 DE AB 于点 E，点 F在边 CD上， DF BE ，连接 AF，（1）求证：四边形 BFDE是矩形；（2）若 CF  ， 3 BF  ， 4 DF  ，求证：AF平分 DAB 5 。 D E A C F B 23. 在平面直角坐标系 xOy 中，直线 y  ( kx b k   与双曲线 0) y  的一个交点为 8 x (2, P m ，与 x轴、y轴分别交于点 A，B。 ) （1）求 m的值； 2 （2）若 PA  AB ，求 k的值。 24. 如图，AB是 O 的直径，过点 B作 O 的切线 BM，弦 / / DA DC （1）求证： ACD （2）连接 OE，若，连接 AC，AD，延长 AD交 BM地点 E. DE  ，求 OE的长. 是等边三角形； 2 CD BM ，交 AB 于点 F，且

25. 阅读下列材料： 2015 年清明小长假，北京市属公园开展以 “清明踏青，春色满园”为主题的游园活动，虽然气温小幅走低，但游客踏青赏花的热情很高，市属公园游客接待量约为 190 万人次，其中玉渊潭公园的樱花，北京植物园的桃花受到了游客的热捧，两公园的游客接待量分别为 38 万人次、21.75 万人次；颐和园、天坛公园、北海公园因皇家园林的厚重文化底蕴与满园春色成为游客的重要目的地，游客接待量分别为 26 万人次，17.6 万人次；北京动物园游客接待量为 18 万人次，熊猫馆的游客密集度较高。 2014 年清明小长假，天气晴好，北京晴好，北京市属公园游客接待量约为 200 万人次，其中，玉渊潭公园游客接待量比 2013 年清明小长假增加了 25%；颐和园游客接待量为 26.2 万人次，比 2013 年清明小长假增加了 4.6 万人次；北京动物园游客接待量为 22 万人次。2013 年清明小长假，玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为 32 万人次、13 万人次、14.9 万人次。根据以上材料回答下列问题：（1）2014 年清明小长假，玉渊潭公园游客接待量为___________万人次。（2）选择统计表或．统计图，将 2013－2015 年玉渊潭公园、颐和园和北京动物园的游客接待量表示出来。 26. 有这样一个问题：探究函数 y  21 x 2  的图象与性质。 1 x 21 x 2 小东根据学习函数的经验，对函数 y  下面是小东的探究过程，请补充完成：  的图象与性质进行了探究。 1 x （1）函数 y  21 x 2  的自变量 x的取值范围是___________； 1 x x … （2）下表是 y与 x的几组对应值。 1 2 15 8 y …   1 2 3 25 6 3 2  1 2   1 3 53 18 1 3 55 18 1 2 17 8 1 3 2 2 5 2 3 … m …

求 m的值；（3）如下图，在平面直角坐标系 xOy 中，描出了以上表中各对对应值为坐标的点，格局描出的点，画出该函数的图象；（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是图象，写出该函数的其他性质（一条即可）：________________。 3(1, 2 ) ，结合函数的 27. 在平面直角坐标系 xOy 中，过点 (0,2) 且平行于 x轴的直线，与直线 y x  交于点 A， 1 点 A关于直线 1x  的对称点为 B，抛物线 1 :C y  2 x  bx  经过点 A，B。 c （1）求点 A，B的坐标；（2）求抛物线 1C 的表达式及顶点坐标；（3）若抛物线 2 : C y  2 ( ax a  与线段 AB恰有一个公共点，结合函数的图象，求 a的取 0) 值范围。 28. 在正方形 ABCD中，BD是一条对角线，点 P在射线 CD上（与点 C、D不重合），连接

AP，平移 ADP  ，使点 D移动到点 C，得到 BCQ ，过点 Q作QH BD 于 H，连接 AH， PH。(1)若点 P 在线段 CD 上，如图 1。 ①依题意补全图 1；②判断 AH与 PH的数量关系与位置关系并加以证明； (2)若点 P在线段 CD的延长线上，且 AHQ  152  ，正方形 ABCD 的边长为 1，请写出求 DP长的思路。（可以不写出计算结果．．．．．．．．．） 29. 在平面直角坐标系 xOy 中， C 的半径为 r，P是与圆心 C不重合的点，点 P关于 O 的反称点的定义如下：若在射线．．CP上存在一点 P ，满足  ，则称 'P 为点 P 关于 C 的反称点，下图为点 P及其关于 C 的反称点 'P 的示意图. 特别地，当点 'P 与圆心C 重合时，规定 CP CP 2 r 0'CP .   （1）当 O 的半径为 1 时： ①分别判断点 (2,1) M ， N 3( 2 其坐标； ,0) ， (1, 3) T 关于 O 的反称点是否存在？若存在，求 ②点 P在直线 y x   上，若点 P关于 O 的反称点 P 存在，且点 P 不在 x轴上， 2 求点 P的横坐标的取值范围；（2）当 C 的圆心在 x轴上，半径为 1，直线 y   3 3 x  2 3 与 x轴，y轴分别交于点

资料库

2015年北京大兴中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料