logo资料库

基于改进PSO-BP神经网络的水厂原水水质预测研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.33M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    5 10 15 25 30 35 40 20 (Beijing University of Posts and Telecommunications，School of Information and Communication PSO - BP neural network ZHANG Yuxin, GONG Ping Engineering，Beijing 100876) 中国科技论文在线 http://www.paper.edu.cn 基于改进 PSO-BP 神经网络的水厂原水水质 预测研究 张钰鑫，龚萍** （北京邮电大学 信息与通信工程学院，北京 10 0876） 摘要：为保障城市供水安全，掌握水厂原水水质的变化趋势，对原水水质污染进行提前预警 和防控，本文采用优化的神经网络模型对水厂原水化学需氧量(Chemical O xygen D emand, COD)进行预测研究。在优化模型中，首先通过粒子群优化算法(Particle Swarm Optimization, PSO)改善传统 BP 神经网络在全局搜索能力方面的缺陷，然后基于 PSO-BP 算法，引入随迭 代次数非线性变化的动态惯性权重，有效提升优化算法的收敛速度，增强泛化能力。本文将 优化的神经网络模型应用于北京地区某水厂原水主要污染物指标 COD 的预测过程，并与传 统 BP 神经网络进行比较。仿真结果表明，基于动态惯性权重的粒子群优化 BP 神经网络能 够有效预测原水水质指标，降低预测误差，更好地面向未来水厂原水水质预测。 关键词：人工神经网络；粒子群优化；动态惯性权重；水质；COD；预测 中图分类号：TP183; X832 Water quality forecast in waterworks based on improved Abstract: In order to ensure the safety of urban water supply and control the change trend of the raw water quality of water plant, this paper uses the optimized neural network model to predict the chemical oxygen demand (COD) of raw water in the water plant. In the optimization model, the PSO-BP(Particle S warm O ptimization - Ba ck P ropagation) a lgorithm is u sed to i mprove t he global search ability of the traditional BP neural network. Then, a dynamic inertia weight which is nonlinear w ith th e ite ration n umber is in troduced to the P SO-BP a lgorithm a nd e ffectively improves t he c onvergence s peed of t he optimization a lgorithm, a nd e nhances t he generalization ability. In this paper, the optimized neural network model is applied to the prediction of the main pollutant COD in a water plant in Beijing, and compared with the traditional BP neural network. Simulation results show that BP neural network based on dynamic inertia weight can effectively predict t he raw water q uality and reduce t he forecast error. Therefore, it can better forecast t he water quality of the future water plant. Key words: artificial neural network; particle swarm optimization; dynamic inertia weight; water quality; COD; forecast 0 引言 随着城市不断扩张，过度使用化肥以及各种工厂和生活污水的肆意排污，中国的水资源 现状不断恶化。2014 年 4 月汉江武汉段水质出现氨氮超标导致汉江武汉段三大水厂自来水 生产被污染，武汉市 260 平方公里面积停止供水。2014 年 8 月重庆巫山县千丈岩水库 280 万立方米水体受到严重污染，导致周边 4 乡镇 5 万余名群众饮水困难。预测自来水水质将来 可能发生的变化,为水厂及预警部门提供可靠的水质变化趋势,为将来可能发生的水质恶化提 作者简介：张钰鑫(1991-)，男，硕士研究生，主要研究方向：数据挖掘与机器学习 通信联系人：龚萍(1975-)，女，博士，副教授，主要研究方向：专网通信，工业信息化，绿色节能通信. E-mail: pgong@bupt.edu.cn - 1 -
    中国科技论文在线 前做好准备具有十分重要的意义[1]。 http://www.paper.edu.cn 45 50 55 目前，国内外对水质进行预测的手段主要有数理统计预测法、灰色系统理论预测法、神 经网络模型预测法、水质模拟模型预测法、混沌理论预测法等[2-7]。然而，这些方法存在泛 化能力差、建模困难、预测精度低等局限性。人工神经网络所具有的高维性、并行分布式处 理性以及自适应、自组织、自学习等优良特性，对于水质预测等复杂问题研究具有良好的适 用性[8]。部分学者使用 BP 神经网络对水质指标进行预测，取得了令人满意的效果[9][10]。 粒子群优化(Particle Swarm Optimization, PSO)算法是一种仿生进化算法，已经广泛应用 于函数优化、神经网络训练等方面，Mendes 等人使用 PSO 算法用于训练前馈神经网络[11]， Lu 等人使用基于 PSO 的神经网络对香港市区环境状况进行分析和预测并于传统 BP 网络算 法进行比较[12]，结果显示 PSO 优化的神经网络效果更好，Chen 等人使用 PSO 算法训练局 部线性小波神经网络(Local Linear Wavelet Neural Network model , LLWNN)，取得了良好的 效果[13]。然而，传统的 PSO 算法存在迭代后期缺少局部搜索能力的缺陷。本研究使用动态 惯性权重优化 PSO-BP 算法，加快算法收敛速度，提高了算法性能，并将其运用在北京地区 M 水厂原水化学需氧量(Chemical Oxygen Demand, COD)预测中，为水厂原水水质预测提供 了新的思路。 1 理论模型 60 1.1 BP 神经网络 65 70 75 BP(Back Propagation)神经网络是一种按误差反向传播算法训练的多层前馈网络，是目前 应用最广泛的神经网络模型之一。BP 神经网络能学习和存贮大量的输入-输出模式映射关 系，而无需事前揭示描述这种映射关系的数学方程。BP 神经网络采用梯度下降法，通过误 差反向传播来不断调整网络的权值和阈值(下称权阈值)，使网络的误差平方和最小。 尽管在理论上神经网络可以实现线性或者非线性函数的映射，但是在实际的运用过程 中，复杂程度高的非线性映射过程往往会存在多个局部最优解，而 BP 神经网络使用梯度下 降法，这就导致初始点（神经网络模型参数初始值）的选取在很大程度上影响到最后的寻优 结果，即“高维曲面上局部极小点的逃离问题”。使用粒子群优化算法来代替梯度下降法训练 网络的权值和阈值，避免了要求函数可微和对函数求导的过程，能够改善 BP 算法的性能， 从而避免上述缺陷。 1.2 粒子群优化算法(PSO) PSO 算法是一种基于种群的优化算法。种群中每个“粒子”的位置是就是优化问题搜索空 间中的一个解，同时具有 D 维空间的一个位置 ix 和速度 iv ,其中 v = v ,v , i i2 ,v 。粒子能够在搜索空间中飞行。PSO 算法随机初始化一群例子的位置和 x = x ,x , i i2 ,x ， ) ( i1 id i1 id ( ) 速度，然后粒子根据自身的最优信息和群体的最优信息动态更新自己的速度和位置，同时用 相关函数计算个体适应度(fitness)评价解的好坏。每次更新后，选出 pbest（个体极值）和 gbest （全局极值）并记录，再根据（1.1）和（1.2）式分别更新例子的速度和位置，通过迭代寻 找最优解 pgbest (0.1) + ( ) ()* + = v k 1 id c Rand 1 * v k id - x k id k ( P x k - ()* id id 1+ = x x k k id id ) + c Rand * 2 + v ( k id 80 0.2) - 2 -
    中国科技论文在线 http://www.paper.edu.cn () 其中， 1c 和为加速常数，它们的作用是使微粒向个体极值 pbest 和全局极值 pgbest 的位置加 Rand 为[0,1]范围内变化的随机数，用来模拟随机扰动。此外，粒子的速度 速运动。定义 iv 还需要被限制在一个范围[ ,v 内，它们决定微粒在解空间中的搜索精度。如果 maxv max 太高，可能会导致微粒在最优解周围震荡无法收敛；如果 maxv 太小，则会导致微粒很容易陷 入局部最优解。 1.3 PSO 优化的 BP 神经网络 v min ] 神经网络的精髓是将网络的实际输出与期望输出间的误差归结为权值和阀值调节，因此 权值和阀值是神经网络中最重要的参数。基于粒子群算法优化的神经网络将神经网络误差作 为粒子群算法的适应度函数。粒子群算法的染色体为 BP 神经网络的权阀值。优化神经网络 的权阀值，使得神经网络训练误差达到最小，有效避免训练陷入局部最优情形。PSO 算法 不像其他算法那样有很多的参数需要不断调整，因此，在实际应用过程中仅调整隐含层节点 的个数及权阀值的大小便可得到不错的计算结果。图 1 为基于粒子群算法优化神经网络的流 程图： 确定BP神经网 络的拓扑结构 初始化BP神经 网络权阈值 输入BP神经网 络初始权阈值 PSO对权阈值进 行编码 BP神经网络训练 误差函数作为PSO 适应函数 粒子速度更新 计算适应度 是否满足 停止条件 获得最优的 权阈值 BP神经网络 权阈值更新 是否训练 停止条件 模型训练结束 图 1 基于粒子群优化 BP 神经网络流程图 Fig. 1 flow chart of BP neural network based on particle swarm optimization 1.4 动态惯性权重优化 PSO-BP 为了提高基本 PSO 算法的收敛性能和求解质量，Shi 和 Eberhart 提出了带有惯性权重的 ω+ = v v k k 1 id id PSO 算法[14]，算法将（1.1）式进一步优化成（1.3）式 * 0.3) 其中，ω 被称为惯性权重（inertia weight），它表示微粒保持运动的惯性，使其有能力探索 新的区域。合适的惯性权重ω 能在减少迭代次数的同时定位最优解，但是确定最优的算法 参数使算法性能最优是一个比较复杂的问题。 c Rand 2 c Rand 1 P x k - id id pgbest k - x k id ) + ) ( ( ()* ( ()* + * 85 90 95 100 Shi 等人提出了惯性权重随迭代次数线性递减的模型[15]。随迭代次数的增加，惯性权重 105 ω 将减小，即ω 满足 - 3 -
    中国科技论文在线 = ω ω ω ω min max max - - ( ) http://www.paper.edu.cn ( 0.4) × k k max 式中， maxω 和 minω 分别为最大惯性权重和最小惯性权重， maxk 为最大迭代次数， k 为当前 迭代的迭代次数。测试结果显示ω 从 0.9 减小到 0.4 时能极大改善算法性能。但是线性权重 算法也存在初期局部搜索能力较弱容易错过全局最优，后期全局搜索能力变弱陷入局部最优 的缺陷。 搜索过程是非线性高度复杂的算法，线性递减惯性权重无法反应实际的搜索过程，不能 充分平衡粒子群优化算法的全局和局部搜索能力。为了改善算法搜索能力，本研究采用了非 线性函数对惯性权重ω 进行修正，即 ω ω ω ω  ×  将（1.5）带入（1.3），可得最终的速度更新公式为： max max = min ( ) - - k k max 2    ( + v k 1 id =     ω ω ω min max max - - ( ) × k k max 2        + v k id c Rand 1 * ()* ( P x k - id id ) ( + c Rand 2 * ()* ( pgbest k - x k id    ) 0.5) 0.6) 2 基于动态惯性权重 PSO-BP 算法在水厂原水水质预测中的应用 M 水厂是北京市某城镇地区唯一的自来水厂，该水厂日供水能力 8.6 万立方米，有多个 来水源。原水水质结构复杂，自来水净化面临挑战。对该水厂原水水质建立预测模型，对水 厂水质净化，保障用水安全有着重要的意义。 2.1 研究数据 本研究数据集使用该水厂原水取水口水质检测数据，数据包含 2014 年 1 月到 10 月的水 质项目检测指标，每月进行两次检测，共 20 组数据。数据有浊度、水温、余氯、PH、氨氮、 亚硝酸盐、耗氧量、溶解性固体总量、硬度、钙、碱度等共计 29 项检测指标。原数据集划 分成两组，前 15 组数据作为训练集对神经网络进行训练，后 5 组数据作为测试集对模型的 性能和效果进行测试。 因为不同指标具有不同的单位和范围，所以首先需要对数据集进行归一化处理，使得数 据全部在[-1,1]范围内。本研究中数据归一化使用 Premnmx 函数： ( f x ) = 2* -1 (2.1) x x - - x max min x min 其中， minx 和 maxx 分别代表输入函数集中某指标的最大值和最小值。在训练结束以后，使用 Postmnmx 函数对输出结果进行反归一化。 2.2 BP 神经网络模型对 COD 进行预测 COD是指在一定条件下水样被强氧化剂氧化时所需氧化剂的量，主要指水体被还原性 物质污染的程度。由于湖泊和水库水体普遍地受到有机物（如蓝藻）污染，因此化学需氧量 可以作为有机物相对含量的指标之一，同时也是河流水质规划的一项重要指标。当水中有机 物含量过高时，会出现三个不利因素：其一，藻类大量繁殖会使水体的PH值增高，酸度下 降，影响混凝效果。其二，藻类增多会堵塞滤池。其三，某些藻类会释放毒素，严重影响饮 - 4 - 110 115 120 125 130 135
    中国科技论文在线 http://www.paper.edu.cn 用者身体健康。水厂处理流程中使用预加氯来氧化原水中的藻类和有机物。然而，预加氯氧 化有机物具有一定的延迟，必须对原水有机物提前预警防控。因此，对水厂原水COD含量 进行预测具有重要的意义。 140 为了与非线性惯性权重 PSO-BP 神经网络模型比较，本研究首先构建了一个 BP 神经网 络，用于对水厂原水 COD 指标进行预测。BP 神经网络采用结构为 28-30-1 的无延迟网络结 构，隐含层节点数设置为 30，隐含层采用双曲正切函数（TRANSIG）作为激发函数，输出 层采用线性（PURELIN）作为激发函数；学习率设置为 0.1，动量因子设置为 0.9；最大迭 代次数设置为 1000，迭代训练误差设置为 1e-5;使用训练集对 BP 神经网络进行训练，训练 函数使用自适应 LR 梯度下降法(Traingda)来对神经网络的权阈值进行更新。BP 神经网络对 训练集数据的拟合曲线如图 2 所示，可以看出 BP 神经网络对数据集有较好的拟合精度。 145 计 O 以 量 氧 耗 2.6 2.4 2.2 2 1.8 1.6 1.4 1.2 1 0.8 0 150 真 实 值 预 测 值 5 时 间 10 图 2 B P 神经网络训练拟合曲线 Fig.2 Training Fitting Curve of BP Neural Network 15 将测试集数据输入训练好的 BP 神经网络，网络的预测效果如图 3 所示。从图中可以看 出 BP 神经网络的预测结果误差较大。 预 测 值 真 实 值 2.6 2.4 2.2 2 1.8 计 O 以 量 氧 耗 1.6 1 1.5 2 2.5 3 时 间 3.5 4 4.5 5 155 Fig.3 Predictive effect of BP neural network 2.3 非线性惯性权重 PSO-BP 神经网络模型对 COD 预测 图 3 B P 神经网络预测效果 如图 1 所示，使用非惯性权重粒子群优化算法来更新 BP 神经网络的权阈值。PSO-BP 网络的隐含层节点数设置为 30，学习因子 1c = 1.49 ， 2c = 1.49 ，粒子群最大迭代次数 maxk = 50 ，最大惯性系数 maxω = 0.9 ，最小惯性系数 minω = 0.4 ；将以上参数带入式（1.6） - 5 -
    中国科技论文在线 http://www.paper.edu.cn 160 有： v = 0.9 -0.5 k+1 id     2 k 50        k  ×   ( ) +1.49* Rand()* pgbest - x k id v +1.49* Rand()* P - x k k id id id ( ) ( 2.2) 165 170 175 180 分别使用（2.2）和（1.2）在迭代过程中更新例子的速度和位置。用 ) 表示一组参数值，向量中的每一维表示神经网络的权阈值，d 代表网络中权阈值的个数。粒 子的适应度函数如式（2.4）所示，为网络的误差函数： i I = Y - y ( ,x id x = x ,x , i i2 i1 2.3) ( i,j i,j j n i=1 I popIndex = I ( i 2.4) 其中，n 代表样本个数， i,jY 表示第 i 个样本的第 j 个理想输出值， i, jy 表示第 i 个样本的第 j 个实际输出值，令 popIndex = 1,2,L, popSize ， popSize 为粒子种群规模，即权阈值个数 d。因为本研究中神经网络的结构为 28-30-1，即网络输出只有 COD 一个指标，因此适应度 函数可以简化为（2.5）： I popIndex n = Y - y ( i i i=1 2.5) 使用相同数据集对动态惯性权重 PSO-BP 神经网络进行训练，PSO 算法迭代次数为 50， 模型进化过程如图 4。其中最佳适应度曲线表示种群中最好（最小）的适应度 pgbest，平均 适应度曲线表示种群所有粒子适应度的均值。非线性惯性权重ω 随迭代次数的额变化如图 5 所示。图 6 表示网络在测试集的预测值和真实值对比曲线，可以看出动态惯性权重优化 PSO-BP 神经网络对水厂原水 COD 有着优秀的预测能力，能够真实反映出 COD 指标的变化 趋势。 度 应 适 5 4.5 4 3.5 3 2.5 2 1.5 1 0.5 0 最 佳 适 应 度 函 数 曲 线 平 均 适 应 度 曲 线 图 5 10 15 20 25 进 化 代 数 30 35 40 45 50 图 4 粒子群进化迭代曲线 Fig.4 Particle swarm evolution iteration curve - 6 -
    中国科技论文在线 http://www.paper.edu.cn 重 权 性 惯 0.9 0.85 0.8 0.75 0.7 0.65 0.6 0.55 0.5 0.45 0.4 0 计 O 以 量 氧 耗 2.6 2.5 2.4 2.3 2.2 2.1 2 1.9 1.8 1.7 1 5 10 15 20 25 迭 代 数 30 35 40 45 50 图 5 惯性权重ω 随迭代次数非线性变化曲线 Fig.6 T he inertia weight changes nonlinearly with the iteration number 预 测 值 真 实 值 1.5 2 2.5 3 时 间 3.5 4 4.5 5 图 6 动态惯性权重 PSO-BP 网络预测效果 Fig.6 Dynamic inertia weight PSO - BP network prediction effect 2.4 结果分析 本研究使用相同的水厂原水水质数据分别训练了传统的 BP 神经网络和动态惯性权重的 PSO-BP 神经网络，并使用了相同的测试集测试两种网络对水质 COD 指标的预测情况，两 种网络的预测数据如表 1 所示。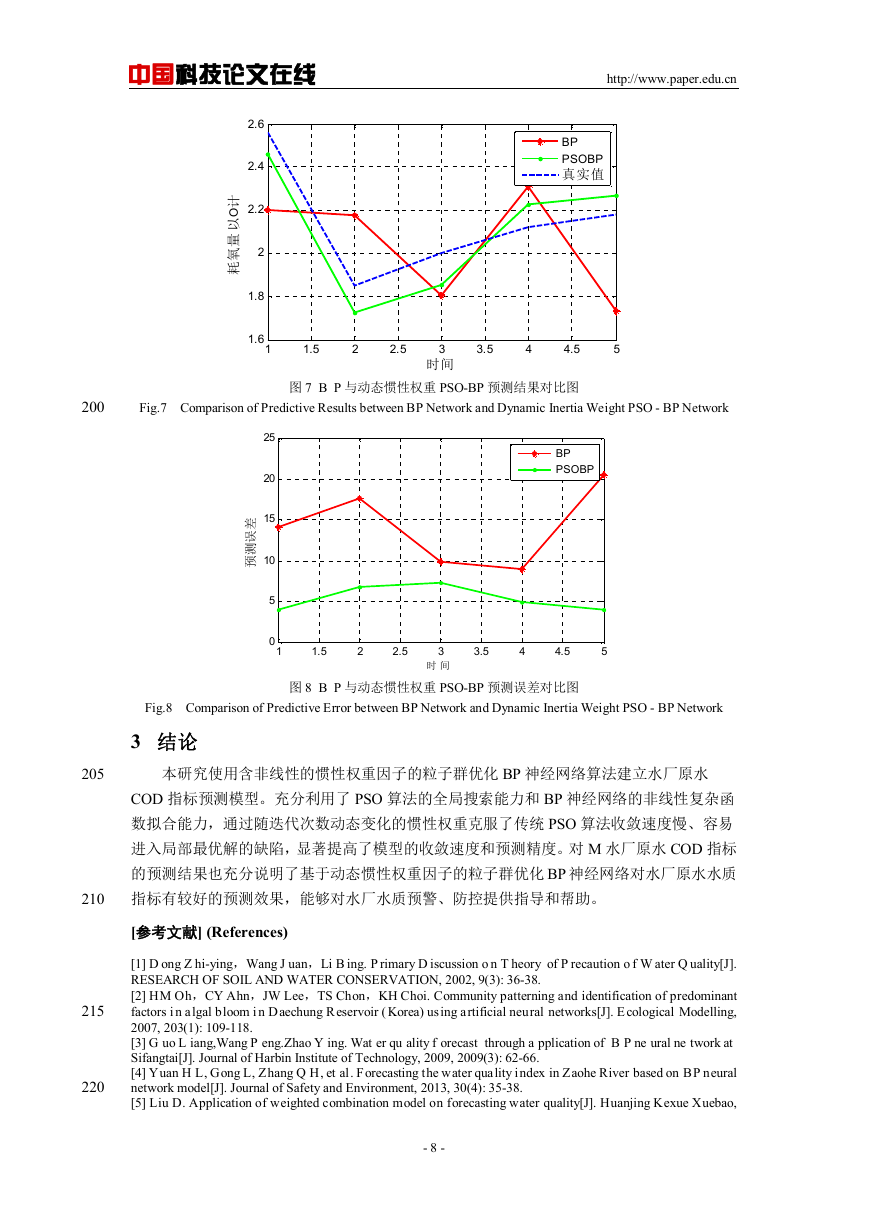 从表 1 以及图 7、图 8 中可以看出，基于动态惯性权重的 PSO-BP 神经网络模型的预测 结果更加切合实际，传统 BP 模型的预测相对误差在 8.9%到 20%之间，平均相对误差为 14.19%；而基于动态惯性权重的 PSO-BP 模型相对误差在 3.9%~7.3%之间，平均相对误差为 5.39%。对于水厂原水水质 COD 指标，基于动态惯性权重的 PSO-BP 模型无论是在最大预 测误差还是在平均相对误差上都远远优于传统的 BP 模型，具有更好的预测精度和泛化能力。 表 1 B P 与优化的 PSO-BP 对原水水质 COD 指标预测数据比较 Tab. 1 Comparison of BP and optimized PSO - BP for COD data of raw water quality 预测序号 CO D 预测值与真实值对比/(mg·L-1) 预测误差对比/% / 1 2.2003 2 2.1753 3 1.8025 4 2.3100 5 1.7333 BP 模型 PSO -BP 模型 真实值 BP 模型 PSO -BP 模型 2.4580 1.7250 1.8540 2.2246 2.2662 2.5600 1.8500 2.0000 2.1200 2.1800 14.0497 17.5859 9.8750 8.9608 20.4895 3.9844 6.7568 7.3000 4.9338 3.9539 - 7 - 185 190 195
    中国科技论文在线 http://www.paper.edu.cn BP PSOBP 真实值 2.6 2.4 2.2 2 1.8 计 O 以 量 氧 耗 1.6 1 1.5 2 2.5 3 时间 3.5 4 4.5 5 图 7 B P 与动态惯性权重 PSO-BP 预测结果对比图 200 Fig.7 Comparison of Predictive Results between BP Network and Dynamic Inertia Weight PSO - BP Network BP PSOBP 25 20 15 10 5 差 误 测 预 0 1 1.5 2 2.5 3 时 间 3.5 4 4.5 5 图 8 B P 与动态惯性权重 PSO-BP 预测误差对比图 Fig.8 Comparison of Predictive Error between BP Network and Dynamic Inertia Weight PSO - BP Network 3 结论 205 本研究使用含非线性的惯性权重因子的粒子群优化 BP 神经网络算法建立水厂原水 COD 指标预测模型。充分利用了 PSO 算法的全局搜索能力和 BP 神经网络的非线性复杂函 数拟合能力，通过随迭代次数动态变化的惯性权重克服了传统 PSO 算法收敛速度慢、容易 进入局部最优解的缺陷，显著提高了模型的收敛速度和预测精度。对 M 水厂原水 COD 指标 的预测结果也充分说明了基于动态惯性权重因子的粒子群优化 BP 神经网络对水厂原水水质 指标有较好的预测效果，能够对水厂水质预警、防控提供指导和帮助。 [参考文献] (References) [1] D ong Z hi-ying，Wang J uan，Li B ing. P rimary D iscussion o n T heory of P recaution o f W ater Q uality[J]. RESEARCH OF SOIL AND WATER CONSERVATION, 2002, 9(3): 36-38. [2] HM Oh，CY Ahn，JW Lee，TS Chon，KH Choi. Community patterning and identification of predominant factors in algal bloom in Daechung Reservoir (Korea) using artificial neural networks[J]. Ecological Modelling, 2007, 203(1): 109-118. [3] G uo L iang,Wang P eng.Zhao Y ing. Wat er qu ality f orecast through a pplication of B P ne ural ne twork at Sifangtai[J]. Journal of Harbin Institute of Technology, 2009, 2009(3): 62-66. [4] Yuan H L, Gong L, Zhang Q H, et al. Forecasting the water quality index in Zaohe River based on BP neural network model[J]. Journal of Safety and Environment, 2013, 30(4): 35-38. [5] Liu D. Application of weighted combination model on forecasting water quality[J]. Huanjing Kexue Xuebao, 210 215 220 - 8 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料