《鲁棒控制》Miu分析与综合方法.pdf-资料库

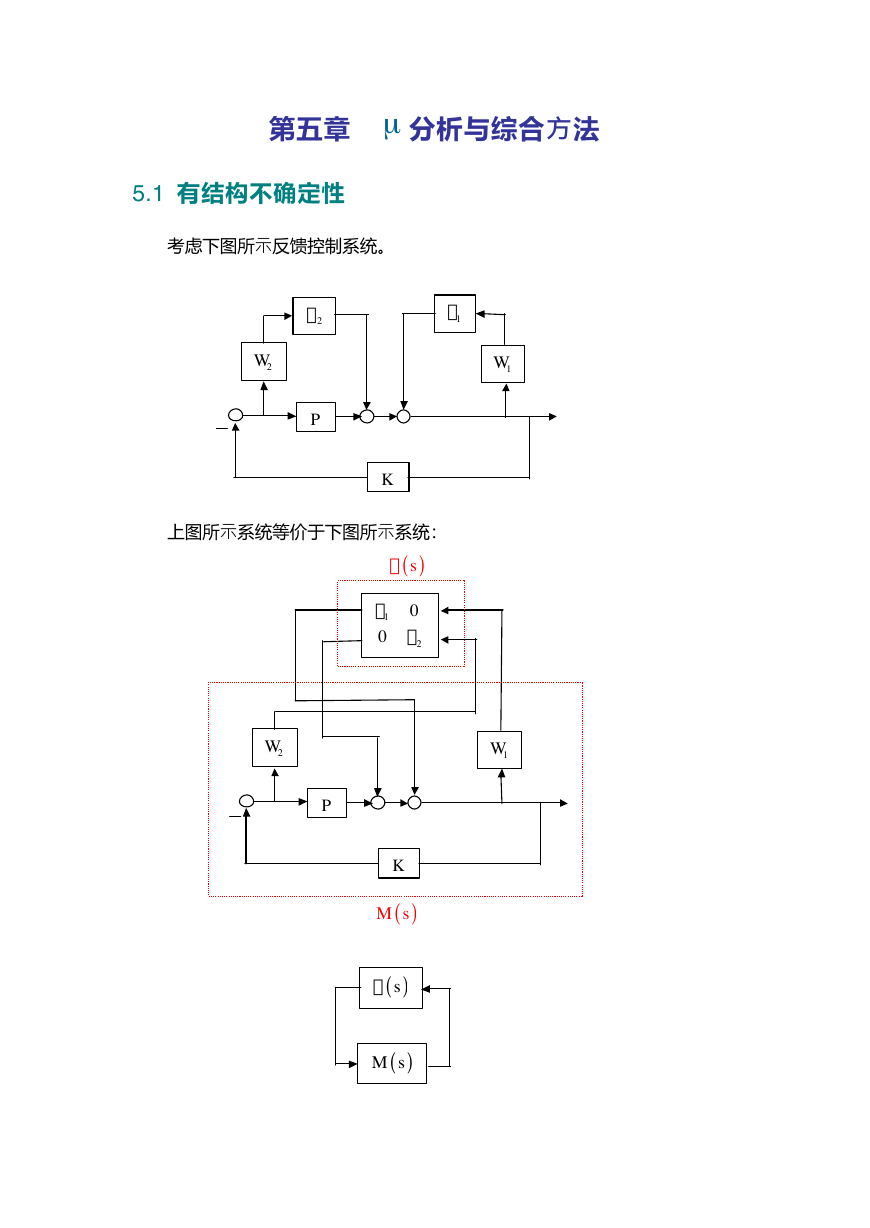
第五章 m 分析与综合方法 5.1 有结构不确定性 1W 1W 1D 2W 2D P D 1 0 0 D 2 ( )sD 考虑下图所示反馈控制系统。上图所示系统等价于下图所示系统： K ( )M s ( )M s 2W P K ( )sD

} 其中的模型摄动 ( )sD 具有对角块结构。有结构摄动 ( )sD =˛ diag = ? { dddDDDd ,I; I,I, 12s1 rrrFi 1 2 2 ? L , ,, j D s L , C m m j j C 称 ? 为结构集合。 s = 1 i + rm n i = j F = 1 j 令 { = DDs D , ? { < =˛ DDs D ? , B? o B ? ( ( ) ) } 1 } 1 5.2 结构奇异值 m 及其性质假设 ( )sD 和 ( )M s 均是稳定的，则当 ( s D 充 ) 分小时，闭环系统是稳定的。 + ˛ C ，使得 ( ) I Ms sD = 0 若存在 s det ( ) 则闭环系统不稳定。显然，当时，即 MD ¥ < 1 M < 1 D 时，闭环系统是稳定的。 ( )sD ( )M s 对于给定的 s 由定义 + s + MMsM j C = :supsup ˛ C ， ( ) = M s ) ( s ( ss ) ( ) = w ( )M s ( ) { ( sDD mindet s ) ( ( ) ) R w 可写成 ( D IMs 1 ( ) 0 ) = , } 为无结构的即 M 的最大奇异值的倒数是导致闭环系统不稳定的（最大奇异值）最小无结构 D 的一个度量。当考虑 D 的结构时，即对于 ( )sD ˛ ? ，定义 · ˛ ˛ £ - Ø ø º ß ¥ ¥ ¥ ¥ ˛ ˛ -

( ( ) M s ) = 1 ( ) 0 ) m ? ( D { ( sDD mindet } ? 为有结构的称之为 M 关于有结构复值不确定性 D 的的最大的结构奇异值。 ( 如果不存在 ( )sD ) = ，则令 ˛ ? ，使得 IM s -= IMs ( ) det ) , D ( 0 m ? ( ) M s ) 0 = 。 ●由定义可证 ( mr M ? ? 其中 ( ●当 { = d ●当 { = ? 因为{ d ( max D B? ) = D ˛ ) M )Ar 表示 A 的谱半径。 C 时，则 ( } m d nI , ? }n n C （即无结构）时，则 ( m ? ( MM M r= D ) ) = 的谱半径。 ) s= ( M ) M 。 } C d nI , ( ) rm MM n n ? C ，所以，对于一般情形， ( s ? ) M ( ) 上述对于结构奇异值的界是保守的：假设 D 0 d = Œ d 1 0 时， ( rms 2 ) == b 0MM, M ( ) ( ) = 。当 M = Œ 0 0 b 0 时， ( rm ) M,M s== 0 ( ) = M ( ) 1 。 1 2 1 2 -= + D I M M = Œ 当 1 2 1 2 (注意： ( det )Mr ( ) 1 d 1 d 2 2 ) 为了减小此保守性，考虑对 M 作变换，其不影响 ( 和 ( 的值。 )Ms )Mm 的值，但会改变 = =˛ U { UUU ? 定义 n n·C 中的两个集合： }n I,I 1 smFm > D C,DD,d,d I L 11 ˛=>˛ iii diagD,,D,dI,,d = D r i r i j L m 1 0 j F 1 F R 0 易知，对于 D ˛ ? ，U ˛ U ， D ˛ D ，成立 ˛ - ˛ · ˛ · ˛ £ £ Ø ø œ º ß Ø ø œ º ß Ø ø - Œ œ œ Œ œ - Œ œ º ß - * - - · * Ø ø º ß

D ( D ? U ) = ( ? ) U U,U, U ) ( = sDsDs D U = D D D D ● 对于任意U ˛ U 和任意 D ˛ D ，成立 ( == ( M U MM U = m ( ) ) ( ) mm ? ? D DM ? m ? 证明： ( detdet D ) = I -MI - M = ( detdet D ) = I -MI - M = 1 1 D MI- M ( ( detdet I - ( ( ( I- M D D ) D ) = DDD D ) D U )( U U det U D ) ( ) )1 ) 1 D 因此关于 ( )Mm? 的界可收紧为 ( ) rm inf D D ( UMMDMD max U U s ) ? ( )1 ●下界为等式，即 ) ( ●当 2 S F+ ( ) = MUM r max U U m ? £ 时，上界为等式，即 3 )1 m ? MDMD inf D D s = ( ( ) 对于一般情形， ( inf ˛ D D ● 计算 )Mm? 近似等于。 )1 ( DMD DMD )1 s s ( inf ˛ D D 不等于 ( DMD )1 s inf ˛ D D ，但对于多数情形， ( )Mm? 与是一凸优化问题，但求 ( UMr ) max ˛ U U 不是凸优化问题。 5.3 结构奇异值 m 与常数线性分式变换设 M 为一复数矩阵，将其分块为 M = Œ 1112 M M M M 2122 定义维数分别与 11M 和 22M 相匹配的结构集合 1? 和 2? ，并定义结构集合： D 1 0 0 D 2 D 112 ? , D 2 ? =˛ ? * * ˛ ˛ ˛ - - - - * * - ˛ ˛ £ £ ˛ - ˛ - - - Ø ø œ º ß Ø ø ˛ Œ œ º ß

( )sD ( )M s ( ) 1 sD ( )M s ( ) 2 sD 非（恒）奇异，即可逆时，线性分式变换(LFT) ( lFM , D 有定义 )2 ) =- DD lFM,MMIM 21112222221 D M ( ) 1 ） 22 I M D 2 ● 当（为适定的）。（注意 ● 定理：（1）对于任意 2D ˛ ( （2）对于任意 2D ˛ ) D 2222 M 证：如果 ( mr ? 非奇异。如果 2 2 22 ( )2 2B? ， ( lFM , D 为适定的 iff ) < Mm 1 ? 2B ?o ， ( lFM , D 为适定的 iff ) ( Mm 1 ? ( = M 2 max D B? 2 )2 < 1 ) 22 2 2 ，则显然，对于任意 2D ˛ 2B? ， I M D 2 22 aD ˛ B? ， l 和 x ，成立 22 2 aM Dxlx= ，其 x= ，因此 I M D 奇异。故 b lFM , D 为适定的，则必有 )2 22 2 22 2 22 ) 1 ) 22 ( 2 < 1 M D 2 ，则 bM Dx ( ) 1 sD I M D 2 a / 2B? ，非奇异，即 ( ，则存在 bD ˛ B? ，且 22 ( r max D B? 2 中 1l ‡ 。令 b = D D l 如果对任意 2D ˛ Mm 。 ? ● 主回路定理： ) 1Mm < ) 1Mm 证明：仅证第一个结论，可类似证明第二个结论。 is D £ ， 1 2 “if”部分：给定 i D ˛ ? ，满足 ( ( ( lFM , ( ( lFM , Mm ? Mm ? )2 lFM , D max D B? 2 max B ?o D 2 ) 1 iff iff 且且 ( ( ) ) ( ( m ? D 2 ? ? 1 1 < m ? 1 22 22 2 2 ( 2 2 i 1 ) ) < ) ) 1 1 D 2 ,= ，定义 i - - - £ ˛ - ˛ ‡ - - ˛ £ £ ˛ £

1 知 22 = D D 1 0 I M D 2 D IM 11112 D MI M 2 21122 D ( 2 DDDD ( MIM 22211112222221 1 ( DD D ) ) < ) ) 1 D 2 1 l 由 ( Mm ? ( detdet 2 22 ) < ) = D =- IMIM I M ( detdet ( detdet IMIFM , 2222 ( ( m lFM , ? 非奇异，故有 max D B? 2 由 =- 1 2 ? 0 D 2 可逆，所以有 M M D D ) ) ( ) 1 ) ( IFM , l )2 D D 1 非奇异，因此，I M D 以及 i D ˛ B? ，知 i ( ) ( 1 < M M max D B? ( mr ? ) = D ˛ “only if”部分：由 ( )MDm 的定义易知 } { ) ( ( ) mm m MM, max M DD D 意味着 ( ) < Mm 1 I M D ，因此 ? 2 ( ) ( =- DDD D IMIMIFM , 0detdetdet )2 ( D ˛ B? ， D D IFM , 非奇异，即 1 l i ) ( ( ) < D m max lFM , ? 2 D B? 2 ) 1Mm < 故对任意 i 2222 1122 1 ( ) ( ) 22 22 ? 1 2 1 2 1 2 可逆，且成立 ) ( ) l 5.4 有结构摄动系统鲁棒稳定性 1w + 1e ( )sD ( )G s 2e + 2w 对于分块结构集合 L DDd ,I; ? ,, 1 定义 { dd I, 11s rrFi diag =˛ s ( M ? ) { =•˛ D ( ) RH L D j , ( ) s, s o D ? C o } m m j j C } C + ●定理：假设 ( )G s ˛ RH ， ( ) D • ˛ M ? 且 ( ) D < ，则有结构摄动反馈系统是 1 b 适定的且内稳定， iff ( b G j ( mw ? sup w R ) ) Ø ø ˛ Œ œ º ß - - - - Ø ø - Œ œ - - º ß - - - - ˛ - - ‡ - „ - - - ˛ · ˛ ¥ ˛ " ˛ ¥ ¥ ˛ £

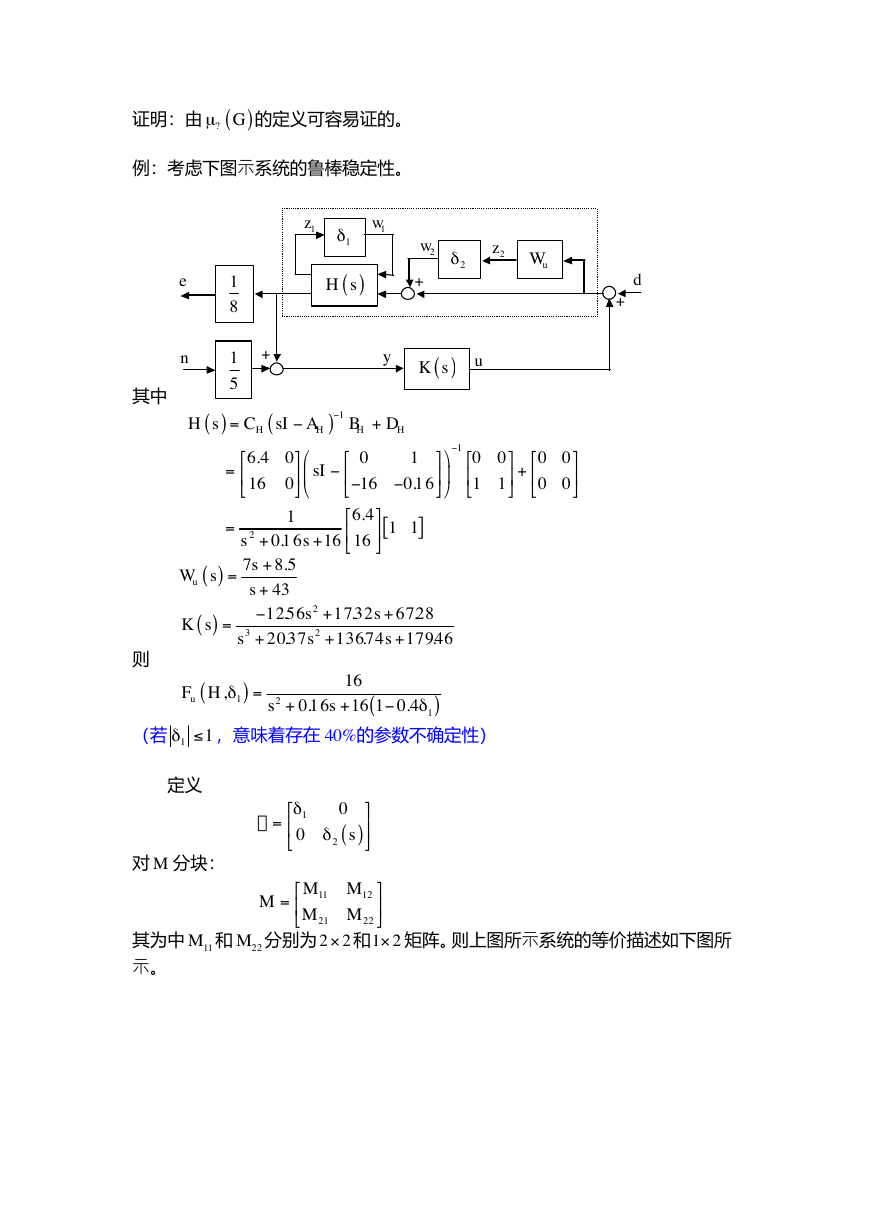
)Gm? 的定义可容易证的。证明：由 ( 例：考虑下图示系统的鲁棒稳定性。其中 1d ( )H s 1 8 1 5 1w 1z + n y e ( ) HsCsIAB =- ( D ) 1 + H + . [ ] 1 1 H sI HH 64001000 0 . 160160 16110 0 6 4 . 16 1 + + 2 0 1616 s s. + 78 5 s . + s 43 -+ 125617326728 + + 3 20371367417946 s.s.s + 2 + 2 .s.s . . =- = ( ) W s u = ( ) K s = 则 2w + 2z 2d uW d + ( )K s u 1 ) d = ( uFH , d £ ，意味着存在 40%的参数不确定性） ( 0161610 4 16 . ++ 2 s.s 1 d ) 1 1 （若 1 定义 D = Œ d 1 0 0 ( ) s d 2 对 M 分块： M = Œ 1112 M M M M 2122 其为中 11M 和 22M 分别为 2 2· 和1 2· 矩阵。则上图所示系统的等价描述如下图所示。 - - Ø ø Ø ø Ø ø Ø ø Œ œ Œ œ Œ œ Œ œ - - º ß º ß º ß º ß Ł ł Ø ø Œ œ º ß - Ø ø œ º ß Ø ø œ º ß

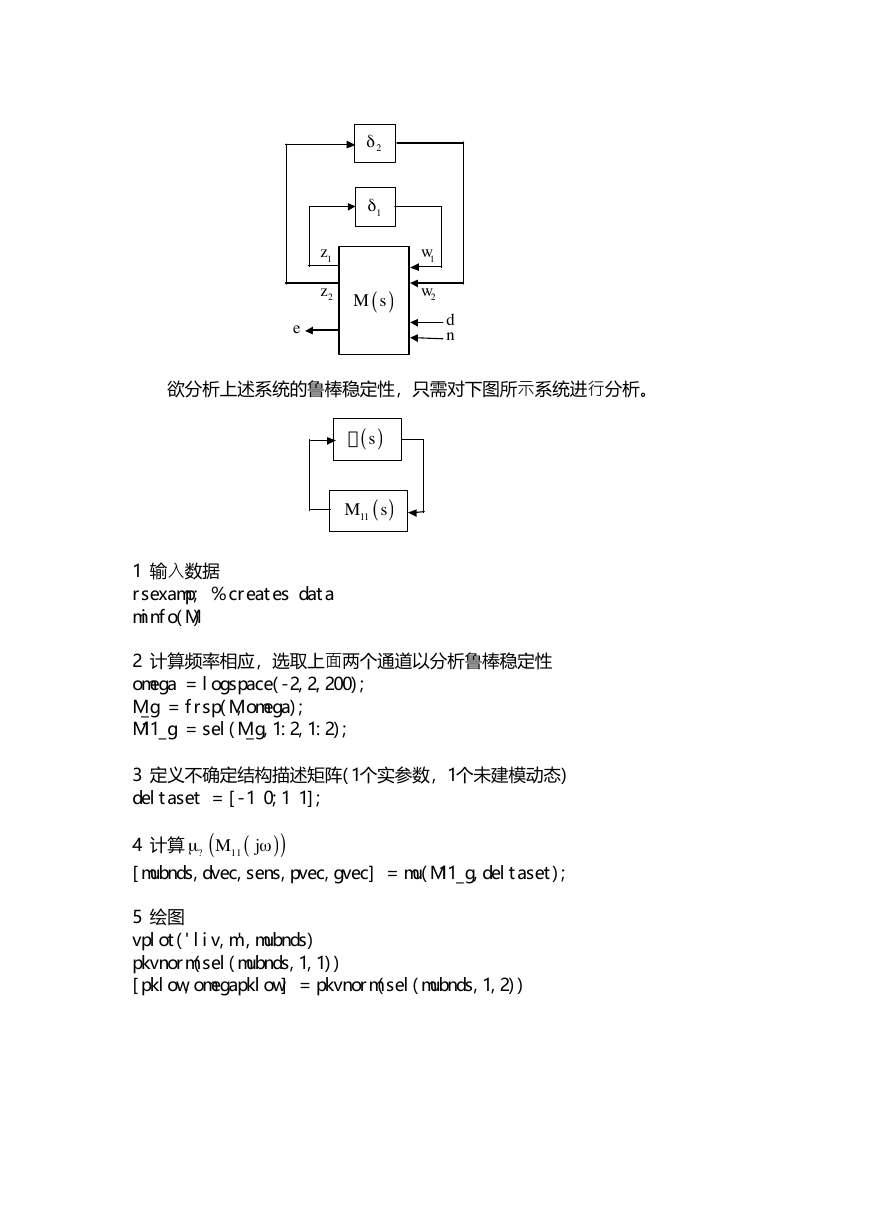
2d 1d 1z 2z ( )M s 1w 2w d n e 欲分析上述系统的鲁棒稳定性，只需对下图所示系统进行分析。 ( )sD ( ) 11M s 1 输入数据 rsexamp; % creates data minfo(M) 2 计算频率相应，选取上面两个通道以分析鲁棒稳定性 omega = logspace(-2,2,200); M_g = frsp(M,omega); M11_g = sel(M_g,1:2,1:2); 3 定义不确定结构描述矩阵(1个实参数，1个未建模动态) deltaset = [-1 0;1 1]; 4 计算 [mubnds,dvec,sens,pvec,gvec] = mu(M11_g,deltaset); 5 绘图 vplot('liv,m',mubnds) pkvnorm(sel(mubnds,1,1)) [pklow,omegapklow] = pkvnorm(sel(mubnds,1,2)) ( w 11M j ) ) ( m ?

资料库

《鲁棒控制》Miu分析与综合方法.pdf

相关推荐

课程资源

热门标签

最新资料