logo资料库

基于不敏卡尔曼滤波的目标跟踪算法.doc

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.38M 资料格式：doc 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    目前工作：不敏卡尔曼滤波主要是利用不敏变换从而获取带不同权值的Sigma粒子，并通过对Sigma粒子
    (1)初始化：
    综合以上步骤，可以得到算法的详细步骤如下：
    期刊
    7.10
    10.23
    基于不敏扩展卡尔曼滤波的目标跟踪算法 一．目标：不敏扩展卡尔曼滤波的过程，流程图，实现步骤。 二．1.了解扩展卡尔曼滤波算法的基本原理及扩展卡尔曼滤波算法产生较大跟踪误差的原 因。 2. 了解不敏扩展卡尔曼滤波算法的基本原理和算法步骤。 3.分析自适应不敏扩展卡尔曼滤波算法的基本原理。 4.通过仿真实验验证了不敏扩展卡尔曼滤波及其自适应算法的有效性。 三．大论文整体思路：第一章：论述；第二章：卡尔曼滤波和扩展卡尔曼滤波；第三章：不 敏扩展卡尔曼滤波算法的改进及仿真实验；第四章：自适应不敏扩展卡尔曼滤波算法的改进 及其仿真实验；第五章：总结。 目前工作：不敏卡尔曼滤波主要是利用不敏变换从而获取带不同权值的 Sigma 粒子，并通过对 Sigma 粒子处理，从而获取对状态的估计，其基本步骤如下: (1)初始化： ˆ X     XE    0 P 0         0  XE    x   0  0 K    0 X 0  X 0 T      i   X X   1-k  1-k   -  -  0   PN PN （2）计算 Sigma 粒子和权值：  i1kX -   1-k  i X  1-k  i X  1-k        W  i     1 N X    W i W W c 0 m 0  2 N N X c  m   x   (3)预测：  1-kk i f k N X   ...,2,1ii1-k ，   ii1-k N  X ， 2...,1 N X 2        -1  2...,2,1i    i 1-k ， N X 
     X  P  KK 1   x2 N  0i  m W i i 1-kk  X 1-kk  2 N x  QWX C I    0i  - 1-kk- i KK 1         T - -  1-kk1-kk    - K  1  i y  KK 1    Y KK 1   h 2 N x  0i  （ i 1-kk ） m W i y i 1-kk （4）更新： P yy   y c W i i 1-kk  - Y KK 1  2 N X  0i   y  i kk 1   Y  KK 1  T   R K 1  i 1-kk - - 1-kk T   c i i Y 1-kk  - 1-kk Wy P  xy X K K  2 N X   0 I  1- PP yy XY  X 1-kk   X  1-kk ZK K     - Y 1-kk- k     P kk   P  KK 1  KPK YY K T k 不敏扩展卡尔曼滤波算法是融合不敏变换和扩展卡尔曼滤波算法的思想，其核心思想是扩展 卡尔曼滤波算法在计算过程中综合利用不敏变换的多样性 Sigma 粒子。根据对不敏卡尔曼滤 波算法的算法时间详细分析，其最耗运算时间的主要是其中预测和更新中的一步以及滤波增 益的计算，因此通过对两个协方差 yyP ， XYP 以及滤波增益 KK 的适当变形计算，从而可以 大大减少算法的运算时间。 预测协方差的计算：利用此式产生 Sigma 粒子：  i K 1  1   i K     0  1  - 1-k   KX 1-k   PN  X i1-k   PN      i1     2...2,1i N  ，，   2...,1 i  ，    X    X      在计算状态预测协方差时，并不是直接利用上述公式，而是利用生成的 Sigma 粒子对其非线 性状态函数 kf 进行线性化。 i1  N N    K K X X X X  F   1 i K  X f T k k 想 k    i X  K  ,...,2,1,0 2 N X 利用第 i 个 Sigma 粒子线性化后的状态函数 i  KF 来计算： 1
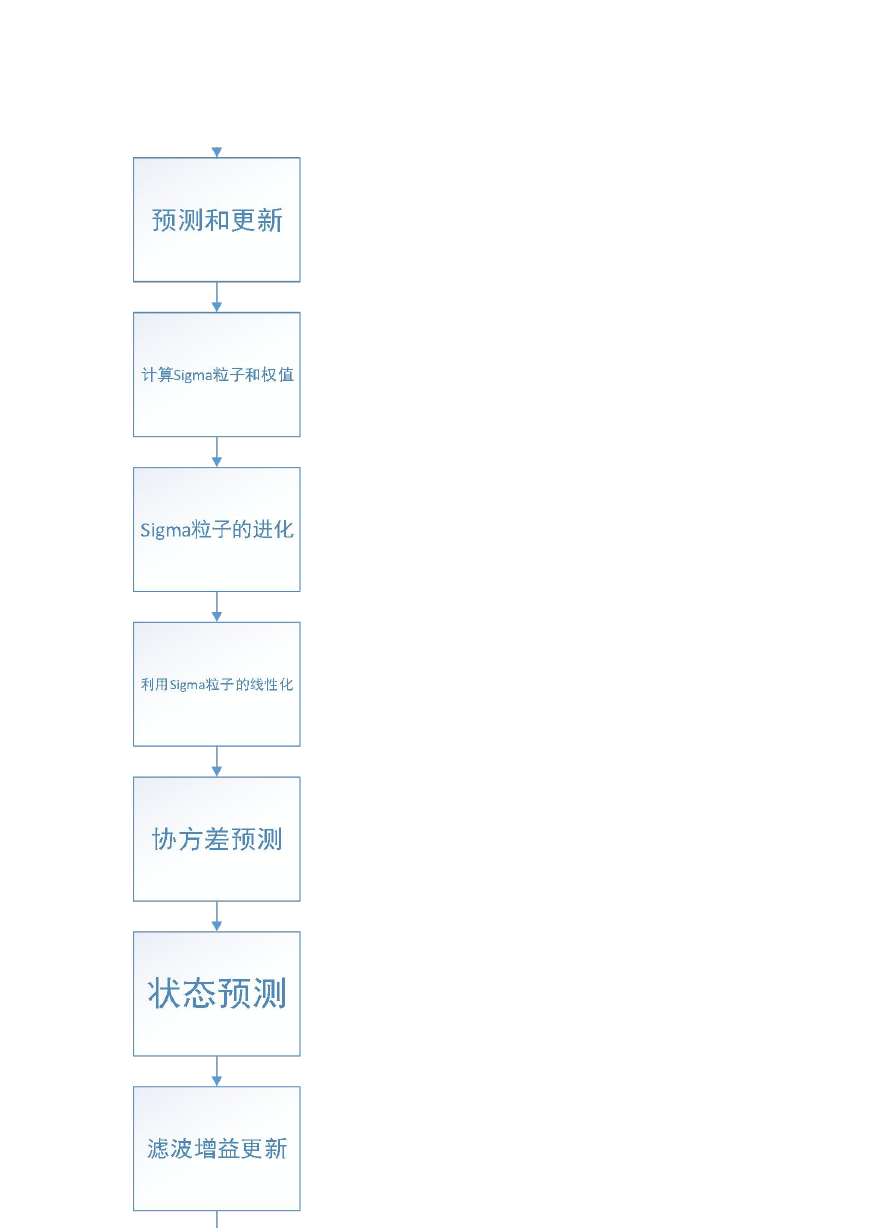
    P k1k  i  i  K F i FP K kk T  i ， 2...,2,1,0 N x 因而，综合上式可以得到状态的预测后验协方差为： P KK 2 N X    1 0i  c PW i K 1  K i  Q K 2.滤波增益的计算 不敏扩展卡尔曼滤波算法不采用不敏卡尔曼滤波增益公式，而采用修正 的滤波增益公式， 胡 如同标准的卡尔曼滤波的增益公式。 K K 1   P K 1  K T K  H   PH K K  1  K H T K  R K 1   1   在该增益公式中，充分利用了预测后验协方差的信息，使得滤波增益可以很好的与目标机动 状态相适应，从而获得较好的滤波精度。 流程图 公式中所有符号和所有变量的含义 综合以上步骤，可以得到算法的详细步骤如 下： (1）初始化：        P 0  X XE       0  0  k  0 X 0   XE    X  0  0    TX 0    ，，X 3048 36500  61 0  km ，， m/s kg/ms 2 P 00         2 2 0 / T   ， ， r r  2 2 2 / 0 / 2 T T  ， ，  r r  2 00  ，，  （2）预测和更新：   14814 /kg 2ms ；T=0.1； r =200m K=1 （a）计算 Sigma 粒子和权值： 修改后： X X X 0 i i    S S S n （（ n( (   表示矩阵   ）） i ) M ss ssM ） i
    平方根的第 i 列； iX 表示第 i 个 Sigma 粒子； iW 表示第 i 个 Sigma 粒子的加权 ss  n  M 值   n     M W O  C W O  m W i  n W i  1  2    n2...,2,1,0 ， c   n2 1   i  这是初始化权重方程，不敏变换中 Sigma 粒子的采样策略，这里采用比例采样，其中 Sigma 粒子数为 2 x N 1 ， 表示采样量 S 有相同的均值和协点，表示相应的权值， xN 是状态向量的维数， m 0W 为 均值的权, 0 cW 为方差的权，为尺度参数， 2  （  N x -k N ） x ，这个公式用于控制 Sigma 点与均值 X 的距离；第一个尺度因子用于控制围绕 X 的 Sigma 分布范围，一般取值 0.001 和 0.1 之间，同时决定采样点的分布条件，在计算中取为 0.1，；k 为第二个尺度因子主要 xN ；在高斯分布的条件下，第三个尺 用于控制方差矩阵的半正定性，一般取 k=0 或者 k=3 度因子取为 2 是最优的，主要用于控制方差矩阵的半正定性。 修改后参数：假设状态向量 S 为 n 维随机变量，并已知其均值 S 和协方差 ssM 。根据 S 和 ssM 选择一种采样策略，得到 S 的近似采样点集 iX ，i=1，...,以及对应的权值 c iW 和 m iW 。 其中，为采样点个数， m iW 为均值加权所用值， c iW 为协方差加权所用权值。本文采用比 例修正对称采样策略。式中：   n2   n-k ；k 为比例参数，可用于调节采样点与 S 的 距离；考虑四阶矩的统计量：k 的有效选取为 n+k=3;为正值的比例缩放因子；为引入  h 高阶项信息的参数，当不使用 h  高阶项信息时，=2；不敏变换:对 iX 中的每个采样 点进行  h 非线性变换，得到变换后的样本点集 iy ， iy =  i h X ，i=1，...，；利用这 组带权值得新样点集 iy 来计算变换后的状态的期望 y 与协方差 yyM ， 1-  y   0i  W m i y i ； M 1-  yy   0i   y-yy-y i  i T ,可以证明上式的采样点集合与状态变方差。 c W i
    （b）Sigma 粒子的进化：   i y   xf k   i  i  1,0 ，，， XN2...2 （c）利用 Sigma 粒子的线性化：  F i 1k     X f T k k KX    （d）协方差预测： X i 1-kk  P P i  k1k  k1k   kk  i F k PW c i  F 2 XN  0i  T  k1k  i  Q k , 方 差 XP ，   k1k    x n2  0i  i   k1k      i w 系 统测 量预 测为 所有  点 测量 预测 的加 权均 值,  点为 2 xn +1 个加权样本点， xn 为状态维数。 （e）状态预测：   k1kx      xw i i   k1k  (f）滤波增益更新： K 1k   P k1k  正滤波增益 （g）状态更新： T k  PHH 1k   T H 1k   R 1k  k1k    1 不敏卡尔曼滤波算法的修  X k1k   !k1k   !k   ZK  P 1k   H !k   X !k  k1k   k1k    X P （h）   HKI  !k  !k!k   1k  k ，跳转至 a
    kX 是目标的状态矢量； KZ 表示测量矢量； kf ， 1kh  分别表示系统的状态模型和测量模型； kK 表示滤波增益； yyPP xy 分别表示两个协方差； kQ 为状态噪声；  KH 是非线性函数 kh （ X ）在预测状态 k X 1-kk 下的雅克比函数 1kk P 表示预测协方差信息；  X KK 是状态矢量 kkX 的无偏估计 ； K 中-表示先验，  K 中  表示估计（百度） 第四章： UKF（不敏卡尔曼滤波）；EKF（扩展卡尔曼滤波） 1.扩展卡尔曼滤波基本原理：对非线性函数围绕中心点进行泰勒级数展开，并认为二阶以上 展开项在整个展开级数中所占能量小，可以忽略，因此只取其一阶展开项替代整个泰勒展开 级数项，即采用截短原理实现非线性函数的线性化，然后利用标准的卡尔曼滤波算法进行迭 代计算。但在某些强非线性系统或非线性系统存在不连续点时，其雅克比函数不存在，扩展 卡尔曼滤波精度变差，滤波器甚至发散。 2.不敏卡尔曼滤波（UKF）,UKF 的核心是利用不敏变换（UT）求取 Sigma 粒子，再把 Sigma 粒子通过非线性函数直接求取粒子的进化值，而避免了求取非线性函数的雅克比函数。 3.文献证明利用不敏卡尔曼滤波的精度可以达到二阶泰勒级数展开式，即不敏卡尔曼滤波比 扩展卡尔曼滤波拥有更好的精度和更大的应用范围。但 UKF 的运算时间比 EKF 大得多，因 此限制了 UKF 在实时性较高的系统中应用。 4.基于上述分析，提出了一种基于不敏扩展卡尔曼滤波的目标跟踪算法，其主要思想是把原 来不敏卡尔曼滤波中状态协方差以及状态和测量值的互协方差的多项矢量相乘转换成多个 相加的计算，从而减少整个算法的运算时间。 5.不敏扩展卡尔曼滤波算法是融合 UT 变换和 EKF 算法的思想，其核心思想是在 EKF 在计算 过程中，综合利用 UT 变换的多样性 Sigma 粒子。根据对 UKF 算法的算法时间度详细分析， 其最耗时间的两个式子适当变形，从而可以大大减少算法的运算时间。（其中改变的两个点 是两个协方差的预测以及滤波增益）。 第三章： 1.基于滤波增益修正的不敏卡尔曼滤波跟踪算法。首先分析了不敏变换的基本原理和对不敏 变换中的 Sigma 粒子采取不同采样策略。利用自适应估计误差尺度因子 s，实时调整误差协 方差 kQ ，并利用修正后的滤波增益更新目标状态和协方差，当目标作强机动时，使得修正 计算后的滤波增益比不敏卡尔曼滤波算法的滤波增益调整更符合目标的机动状态；之后，详 细分析了滤波跟踪模型的克拉-美罗界。最后，通过仿真实验验证了该算法的有效性。补充： 克拉-美罗界是对于参数估计问题提出的，为任何无偏估计量的方差确定了一个下限。无偏 估计量的方差只能无限制的逼近 CRB 而不会低于 CRB，因此这个界也可以称为 CRLB，意为 克拉美罗下界。
    2.卡尔曼滤波的自然扩展即为扩展卡尔曼滤波，扩展卡尔曼滤波采用截短原理将非线性化的 线性化，求取雅克比函数，但是当有不连续点的时候其雅克比函数不存在。此时，文献提出 了不敏卡尔曼滤波，不敏卡尔曼滤波的核心是利用不敏变换（UT）求取 Sigma 粒子，再把 Sigma 粒子通过非线性函数直接求取粒子的进化值，而避免了求取非线性函数的雅克比函 数，文献证明不敏卡尔曼滤波的精度可以达到二阶泰勒级数展开式，即不敏卡尔曼滤波具有 比扩展卡尔曼滤波更好的精度和更大的应用范围。 3.不敏卡尔曼滤波的增益与两个协方差有关，即状态协方差，状态和测量值的互协方差。缺 点是：对状态噪声协方差和测量协方差是依靠先验知识获取，当这两个先验获取的协方差与 实际不一致时，会造成滤波增益落后与目标的实际状态，从而引起较大的跟踪误差。 4.不敏变换：不敏变换的主要思想是近似概率分布而不是近似非线性函数，其核心思想是： 利用状态的均值和方差，采用某种采样策略获取确定性的点集 S（称为 Sigma 粒子）来表征 目标状态的分布，并对每个 Sigma 粒子进行某种变换（这种变换其实就是状态的转移方式）， 利用变换后的 Sigma 粒子的加权组合（权值由采样策略确定）来估计状态变换后的统计特性， 从而避免了计算非线性函数的雅克比矩阵。 5.利用线性化函数代替非线性函数（如 EKF）的方法，其转换后的均值和方差偏离真实值和 方差较大：而利用不敏变换后得到的状=态均值和方差更接近状态的真实均值和方差，精度 高于非线性函数的线性化处理。 6.自适应不敏卡尔曼滤波算法的基本原理也是利用不敏变换得到 Sigma 粒子，把 Sigma 粒子 应用到 EKF 算法中的预测状态协方差的计算，从而获得较为精确的预测状态协方差。只是在 滤波修正后，利用每次滤波过程中得到的残差信息，自适应调整两个噪声协方差 KR 和 kQ ， 从而获得比 UKF 更好的滤波跟踪性能和较快的运算速度。 期刊 1.传统的不敏卡尔曼滤波在对极-直角坐标变换中的误差进行分析时，采用了线性近似的简 单方式，当量测方位误差较大时，无法准确估计出实际的直角坐标位置与误差协方差矩阵， 本无提出无偏估计的不敏卡尔曼滤波，以抑制方位误差对估计结果的影响。仿真结果表明， 本文方法可有效降低方位误差影响，提升目标跟踪的定位精度。 2.不敏变换（UT）基于这样的思想，即用固定数量的参数去近似一个高斯分布比近似任意的 非线性函数或变换更容易。即在原先状态分布中按某一规则取一些点，使这些点的均值和协 方差等于原状态分布的均值和协方差，将这些点带入非线性函数中，相应得到非线性函数值 点集，通过这些点集求取变换后的均值和协方差。 7.10 1.（1）仿真模型初始化条件 X  1k 1       T 0 010 100      X k —  0    XDT   0        g-  k  v k （a）
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料