logo资料库

一维黎曼问题.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：doc 举报 版权申诉
第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
资料共12页，剩余部分请下载后查看
    A-1利用两步差分格式求解一维
    2.基本方程组、初始条件和边界条件
    （A.3）
    3.二阶精度差分格式
    4.计算结果分析
    A-2 一维问题数值计算源程序
    E[0]=U[1];
    T=0;
    ! MacCormack1D.for
    GAMA=1.4
    PI=3.1415926
    J=M
    TT=0.4
    T=0
    !人工黏性项
    附录 A 一维 Riemann 问题数值解与计算程序 一维Riemann 问题，即激波管问题，是一个典型的一维可压缩无黏气体动力 学问题，并有 解析解。对它采用二阶精度MacCormack 两步差分格式进行数值求 解。同时，为了初学者入门和练习方便,这里给出了用 C 语言和Fortran77 编写的 计算一维Riemann 问题的计算程序，供大家学习参考。 A-1 利用 MacCormack 两步差分格式求解一维Riemann问题 1.一维Riemann 问题 一维 Riemann 问题实际上就是激波管问题。激波管是一根两端封闭、内部充 满气体的直管，如图 A.1 所示。在直管中由一薄膜将激波管隔开，在薄膜两侧充 有均匀理想气体（可以是同一种气体， 也可以是不同种气体），薄膜两侧气体 的压力、密度不同。当 0t 时，气体 处于静止状态。当 0 t  时，薄膜瞬时 突然破裂，气体从高压端冲向低压端， 同时在管内形成激波、稀疏波和接触间 断等复杂波系。 2.基本方程组、初始条件和边界条件 图 A.1 激波管问题示意图 设气体是理想气体。一维 Riemann问题在数学上可以用一维可压缩无黏气体 Euler 方程组来描述。在直角坐标系下量纲为一的一维Euler 方程组为： 其中 u u  t        f  x     u    E  ,   0 , 1 1x    f       u  2 u p   ( ) E p u       (A.1) (A.2) 这里 、u 、 p 、 E 分别是流体的密度、速度、压力和单位体积总能。理想气体 状态方程： p        1   e  1  E     1 2  u  2 2  v     （A.3） 初始条件： 1   1, u 1  0, p 1 1  ； 2   0.125, u 2  0, p 2  。 0.1 -A.1-
    边界条件： x   和 1x  处为自由输出条件， 0 u 1 u , 1 u N  。 u  1 N 3.二阶精度MacCormack 差分格式 MacCormack 两步差分格式：  1 2  u n j   1 2 n j  u n j u n u j  1  2  1  u n j    r    n f j 1 2  f n 1 j  r n  1 j  f     1 2  1 2 n j f     (A.4) 其中 r  t  x  。计算实践表明， MacCormack 两步差分格式不能抑制激波附近非物 理振荡。因此在计算激波时，必须采用人工黏性滤波方法： n u , i j  n u , i j   n u   1, i j 1 2  n 2 u , i j  n u 1, i  j  (A.5) 为了在激波附近人工黏性起作用，而在光滑区域人工黏性为零，需要引入一个与 密度（或者压力）相关的开关函数：   i 1      1 i      1 i        i 1  i i i i (A.6) 由式(A.6) 可以看出，在光滑区域，密度变化很缓，因此值也很小；而在激波 附近密度变化很陡，值就很大。带有开关函数的前置人工黏性滤波方法为： n u , i j  n u , i j  n u   1, i  1 2  n 2 u , i j  n u 1, i  j j  (A.7) 其中参数往往需要通过实际试算来确定，也可采用线性近似方法得到：    | t a x  |  1    | t a x  |    (A.8) 由于声速不会超过 3，所以取| 4.计算结果分析 a  ，在本计算中取 0.25 | 3  。 计算分别采用标准的 C 语言和 Fortran77 语言编写程序。计算中网格数取 1000 ，计算总时间为 0.4 T  时刻的密度、速度和压力分布 如图 A.2（ C 语言计算结果）和图 A.3（ Fortran77 语言计算结果）所示。采用两 T  。计算得到在 0.4 种不同语言编写程序所得到的计算结果完全吻合。 从图 A.2 和图 A.3 中可以发现，MacCormack 两步差分格式能很好地捕捉激波， 计算得到的激波面很陡、很窄，计算激波精度是很高的。采用带开关函数的前置 -A.2-
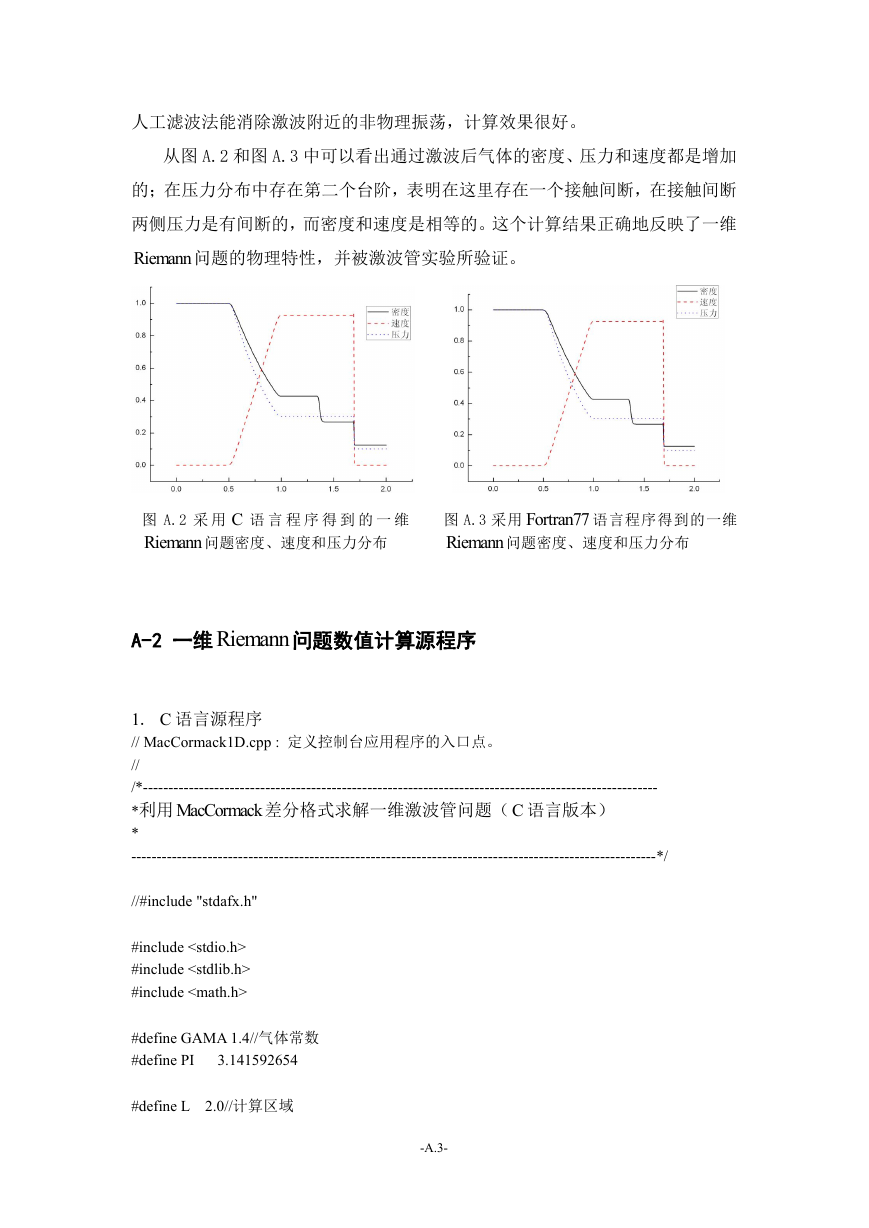
    人工滤波法能消除激波附近的非物理振荡，计算效果很好。 从图 A.2 和图 A.3 中可以看出通过激波后气体的密度、压力和速度都是增加 的；在压力分布中存在第二个台阶，表明在这里存在一个接触间断，在接触间断 两侧压力是有间断的，而密度和速度是相等的。这个计算结果正确地反映了一维 Riemann 问题的物理特性，并被激波管实验所验证。 图 A.2 采 用 C 语 言 程 序 得 到 的 一 维 Riemann 问题密度、速度和压力分布 图 A.3 采用 Fortran77 语言程序得到的一维 Riemann 问题密度、速度和压力分布 A-2 一维 Riemann 问题数值计算源程序 1. C 语言源程序 // MacCormack1D.cpp : 定义控制台应用程序的入口点。 // /*----------------------------------------------------------------------------------------------------- *利用 MacCormack 差分格式求解一维激波管问题（ C 语言版本） * -------------------------------------------------------------------------------------------------------*/ //#include "stdafx.h" #include #include #include #define GAMA 1.4//气体常数 #define PI 3.141592654 #define L 2.0//计算区域 -A.3-
    #define TT 0.4//总时间 #define Sf 0.8//时间步长因子 #define J 1000//网格数 //全局变量 double U[J+2][3],Uf[J+2][3],Ef[J+2][3]; /*------------------------------------------------------- 计算时间步长 入口: U，当前物理量，dx，网格宽度； 返回: 时间步长。 ---------------------------------------------------------*/ double CFL(double U[J+2][3],double dx) { int i; double maxvel,p,u,vel; maxvel=1e-100; for(i=1;i<=J;i++) { u=U[i][1]/U[i][0]; p=(GAMA-1)*(U[i][2]-0.5*U[i][0]*u*u); vel=sqrt(GAMA*p/U[i][0])+fabs(u); if(vel>maxvel)maxvel=vel; } return Sf*dx/maxvel; } /*------------------------------------------------------- 初始化 入口: 无； 出口: U， 已经给定的初始值， dx, 网格宽度。 ---------------------------------------------------------*/ void Init(double U[J+2][3],double & dx) { int i; double rou1=1.0 ,u1=0.0,p1=1.0; //初始条件 double rou2=0.125,u2=0.0,p2=0.1; dx=L/J; for(i=0;i<=J/2;i++) -A.4-
    { U[i][0]=rou1; U[i][1]=rou1*u1; U[i][2]=p1/(GAMA-1)+rou1*u1*u1/2; } for(i=J/2+1;i<=J+1;i++) { U[i][0]=rou2; U[i][1]=rou2*u2; U[i][2]=p2/(GAMA-1)+rou2*u2*u2/2; } } /*------------------------------------------------------- 边界条件 入口: dx，网格宽度； 出口: U， 已经给定的边界。 ---------------------------------------------------------*/ void bound(double U[J+2][3],double dx) { int k; //左边界 for(k=0;k<3;k++)U[0][k]=U[1][k]; //右边界 for(k=0;k<3;k++)U[J+1][k]=U[J][k]; } /*------------------------------------------------------- 根据 U 计算 E 入口: U， 当前 U 矢量； 出口: E， 计算得到的 E 矢量， U、E 的定义见 Euler 方程组。 ---------------------------------------------------------*/ void U2E(double U[3],double E[3]) { double u,p; u=U[1]/U[0]; p=(GAMA-1)*(U[2]-0.5*U[1]*U[1]/U[0]); E[0]=U[1]; E[1]=U[0]*u*u+p; E[2]=(U[2]+p)*u; } -A.5-
    /*------------------------------------------------------- 一维 MacCormack 差分格式求解器 入口: U， 上一时刻的 U 矢量，Uf、Ef，临时变量， dx，网格宽度，dt, 时间步长； 出口: U， 计算得到的当前时刻 U 矢量。 ---------------------------------------------------------*/ void MacCormack_1DSolver(double U[J+2][3],double Uf[J+2][3],double Ef[J+2][3],double dx,double dt) { int i,k; double r,nu,q; r=dt/dx; nu=0.25; for(i=1;i<=J;i++) { q=fabs(fabs(U[i+1][0]-U[i][0])-fabs(U[i][0]-U[i-1][0])) /(fabs(U[i+1][0]-U[i][0])+fabs(U[i][0]-U[i-1][0])+1e-100); //开关函数 for(k=0;k<3;k++) Ef[i][k]=U[i][k]+0.5*nu*q*(U[i+1][k]-2*U[i][k]+U[i-1][k]);//人工黏性项 } for(k=0;k<3;k++) for(i=1;i<=J;i++)U[i][k]=Ef[i][k]; for(i=0;i<=J+1;i++)U2E(U[i],Ef[i]); for(i=0;i<=J;i++) for(k=0;k<3;k++) Uf[i][k]=U[i][k]-r*(Ef[i+1][k]-Ef[i][k]); //U(n+1/2)(i+1/2) for(i=0;i<=J;i++)U2E(Uf[i],Ef[i]); //E(n+1/2)(i+1/2) for(i=1;i<=J;i++) for(k=0;k<3;k++) U[i][k]=0.5*(U[i][k]+Uf[i][k])-0.5*r*(Ef[i][k]-Ef[i-1][k]); //U(n+1)(i) } /*------------------------------------------------------- 输出结果, 用 Origin 数据格式画图 入口: U， 当前时刻 U 矢量，dx， 网格宽度； 出口: 无。 -A.6-
    ---------------------------------------------------------*/ void Output(double U[J+2][3],double dx) { int i; FILE *fp; double rou,u,p; fp=fopen("result.txt","w"); for(i=0;i<=J+1;i++) { rou=U[i][0]; u=U[i][1]/rou; p=(GAMA-1)*(U[i][2]-0.5*U[i][0]*u*u); fprintf(fp,"%20f%20.10e%20.10e%20.10e%20.10e\n",i*dx,rou,u,p,U[i][2]); } fclose(fp); } /*------------------------------------------------------- 主函数 入口: 无； 出口: 无。 ---------------------------------------------------------*/ void main() { double T,dx,dt; Init(U,dx); T=0; while(T
    2. Fortran77语言源程序 ! MacCormack1D.for ------------------------------------------------------------------------------------------------------------ !利用 MacCormack 差分格式求解一维激波管问题（ Fortran77语言版本） --------------------------------------------------------------------------------------------------------------*/ program MacCormack1D implicit double precision (a-h,o-z) parameter (M=1000) common /G_def/ GAMA,PI,J,JJ,dL,TT,Sf dimension U(0:M+1,0:2),Uf(0:M+1,0:2) dimension Ef(0:M+1,0:2) !气体常数 GAMA=1.4 PI=3.1415926 !网格数 J=M !计算区域 dL=2.0 !总时间 TT=0.4 !时间步长因子 Sf=0.8 call Init(U,dx) T=0 1 dt=CFL(U,dx) T=T+dt write(*,*)'T=',T,'dt=',dt call MacCormack_1D_Solver(U,Uf,Ef,dx,dt) call bound(U,dx) if(T.lt.TT)goto 1 call Output(U,dx) end !------------------------------------------------------- !计算时间步长 !入口: U， 当前物理量，dx, 网格宽度； !返回: 时间步长。 !------------------------------------------------------- -A.8-
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料