第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
论文研究-区间多目标优化非支配排序云模型算法.pdf
Computer Engineering and Applications 计算机工程与应用
2017，53（22）
143
区间多目标优化非支配排序云模型算法
陈志旺 1，黄兴旺 2，陈志兴 3，赵子铮 2，黄丽芳 4
CHEN Zhiwang1, HUANG Xingwang2, CHEN Zhixing3, ZHAO Zizheng2, HUANG Lifang4
1. 燕山大学 河北省工业计算机控制工程重点实验室，河北 秦皇岛 066000
2. 燕山大学 国家冷轧板带装备及工业工程技术研究中心，河北 秦皇岛 066000
3. 佳木斯电业局，黑龙江 佳木斯 154002
4. 西部超导材料科技股份有限公司，西安 710018
1.Key Lab of Industrial Computer Control Engineering of Hebei Province, Yanshan University, Qinhuangdao, Hebei
066000, China
2.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Yanshan University,
Qinhuangdao, Hebei 066000, China
3.Jiamusi Electricity Power Bureau, Jiamusi, Heilongjiang 154002, China
4.Western Superconducting Technologies Co., Ltd., Xi’an 710018, China
CHEN Zhiwang, HUANG Xingwang, CHEN Zhixing, et al. Non-dominated sorting cloud model algorithm for inter-
val multi-objective optimization. Computer Engineering and Applications, 2017, 53（22）：143-149.
Abstract：A kind of Non-dominated Sorting Cloud Model Algorithm（NSCMA）for solving interval multi-objective opti-
mization is proposed, in which cloud model is used to improve the NSGA-II algorithm. Firstly, genetic operator such as
crossover and mutation in conventional NSGA-II is replaced by normal cloud operator, and offspring cloud droplets are
derived from random parent in initial cloud cluster. Secondly, generated cloud droplets are disposed and kept based on
constraint conditions, so infeasible solution doesn’t be left in the next algorithm. Finally, the feasible solution is sorted by
interval dominant relationship, and then the crowding distance of incomparable same order solution is calculated. The sim-
ulations results have verified the effectiveness of the designed algorithm.
Key words：multi-objective optimization; interval programming; constrained optimization problem; cloud model; NSGA-II
摘 要：针对区间多目标优化问题，利用云模型对 NSGA-II 算法进行改进，提出一种非支配排序云模型算法（NSCMA）。
首先，从初始云团中随机选取一个云滴作为父代，通过正态云算子生成子代云滴，用来替代传统 NSGA-II 遗传操作
中的交叉和变异 ；其次，用约束条件对生成的云滴进行筛选处理，避免不可行解进入下一步算法 ；最后，运用区间占
优关系对满足约束条件的解进行占优排序，对无法比较的同序值解计算拥挤距离。仿真结果验证了所设计算法的
有效性。
关键词：多目标优化 ；区间规划 ；约束优化问题 ；云模型 ；NSGA-II
文献标志码：A 中图分类号：TP18
doi：10.3778/j.issn.1002-8331.1606-0383
1 引言
在现实生活、工程等领域，存在许多问题需要在给
定区域上对多个目标函数同时进行优化，这类问题被
称 为 多 目 标 优 化 问 题（Multi- Objective Optimization
基金项目：国家自然科学基金（No.61573305，No.61403331）；河北省自然科学基金青年基金（No.F2014203099）；燕山大学青年教
师自主研究计划课题（No.13LGA006）。
作者简介：陈志旺（1978—），男，博士，副教授，研究领域为多目标优化，多旋翼飞行器控制；黄兴旺（1991—），男，硕士，研究领域
为多目标优化，E-mail：xingwang22@foxmail.com；陈志兴（1976—），男，工程师，研究领域为电力系统自动化；赵子铮
（1990—），男，硕士，研究领域为多目标优化；黄丽芳（1982—），女，助理工程师，研究领域为质量检验及热处理，PID 控制。
收稿日期：2016-06-27 修回日期：2016-08-18 文章编号：1002-8331（2017）22-0143-07
CNKI 网络优先出版：2016-12-02, http://www.cnki.net/kcms/detail/11.2127.TP.20161202.1503.040.html
计算机工程与应用www.ceaj.org
144
2017，53（22）
Computer Engineering and Applications 计算机工程与应用
Problems，MOP）[1]。近年来，很多学者使用进化算法求
解 MOP，而在实际工程优化问题中，由于环境或者系统
自身的原因，很难获得所需要精确模型，因此研究不确
定模型的优化求解更有意义。通常可将不确定参数分
为三类，即随机变量、模糊变量和区间变量，相比于前两
者，采用区间变量时，只需要知道该区间的上下限或者
中点和半径，因此不确定区间多目标优化问题比随机优
化和模糊优化更有意义。文献[2]利用土地资源配置模
型改进了现有的多目标优化，从而实现了对长江三角洲
的土地资源进行合理规划。文献[3]利用区间规划的方
法将不确定多目标优化转换成确定多目标优化，而文
献[4]对区间数顺序关系进行了重新定义，使用不同的
区间指标关系，将多目标优化问题转化成单目标优化问
题。文献[5]利用最大最小算子法，构建了模糊几何加
权单目标规划模型的等价模型，通过求解等价模型的最
好模型和最差模型，得到非劣解及目标函数最优值区间
的求解方法。在将不确定性优化问题转化成确定性优
化问题和将多目标问题转化成单目标问题求解的过程
中，可能会丢失部分优化信息。而文献[6]中 Wang 提出
一类解决含区间参数多目标优化问题的粒子群优化算
法，通过定义信度空间的知识描述形式，来引导算法的
进化方向。文献[7]中 Chen 等将区间规划引入到 NSGA-
II 算法中，构成区间 NSGA-II 算法，实现了对多目标优
化问题的直接求解，避免了问题转化过程中的信息丢
失，增加了求解精度。
描述不确定性另一种十分重要的模型是云模型[8]。
云模型的应用十分广泛，很多学者将云模型应用于多目
标优化问题中，文献[8]在云模型的基础上提出学习云
算子，来控制种群的遗传和进化，保证了遗传进化的稳
定倾向性和随机性。文献[9]利用正态云模型生成云滴
的随机性特点，分别对交叉、变异、拥挤距离算子进行改
进，使算法既具有传统的趋势性，又满足快速寻优能力，
并且通过求解多目标背包问题，验证了算法的有效性。
文献[10]针对 NSGA-II 识别非支配个体较慢和个体比较
次数较多的不足，引入云模型进化策略，利用云模型具
备的模糊性和随机性的优良特性维护进化种群，提高非
支配解分布的广度和均匀度。
以上云模型在多目标优化中应用都是对确定数进
行优化，本文结合 NSGA-II 算法基本思想和云模型在知
识表达过程兼具随机性和稳定性的优良特性，将云模型
应用在区间多目标优化上，利用云模型对 NSGA-II 算法
进行改进，用云算子 [11]替换 NSGA-II 的遗传操作，提高
了算法的搜索能力和 Pareto 前沿的均匀性。
2 问题描述
带约束区间多目标优化问题的一般表达式为：
)x,u
)
Q:min
x
s.t. gj(
hk(
x = (
u = (
)x,u = (
)x,u ,f2(
f1(
F(
)x,u ,⋯,fz(
]
)x,u ≥ aj =[
aj,-aj ,j = 1,2,⋯,m
-
)x,u ≥ bk =[
]-
bk,-bk ,k = 1,2,⋯,n
)
x1,x2,⋯,xq ∈ X ⊂ Rq,
xi =[
]-
xi,-xi ,i = 1,2,⋯,q
u1,u2,⋯,up ⊂ R p,
ul =[
)
]-
ul ,-ul ,l = 1,2,⋯,p
)x,u 为目标函数向量，fz(
（1）
)x,u 为第 z 个区间
其中，F(
目标函数。 X 为 q 维决策空间，x = (
x1,x2,⋯,xq 为 q
维决策向量（ xs 为第 s 个决策向量），决策向量也可称为
xi 和 -xi 为变量 xi 的上
解，xi 是决策向量第 i 个变量，-
下边界。 u = (
u1,u2,⋯,up 为 p 维参数向量，ul 是参数
ul 和 -ul 为 变 量 ul 的 上 下 边 界 。
向 量 的 第 l 个 变 量 ，-
gj(
)x,u 是第 k 个约
束区间等式。
)x,u 是第 j 个约束区间不等式，hk(
)
)
2 ，
ar = aˉ - -a
]
-- -----fz(
)x
-- -----gj(
)x
ù
û
]
-- -----hk(
)x
定 义 1 对 于 一 个 区 间 数 a = [
)x,u =[
)x ,-
fz(
-- -----
-
)x ,-
)x,u = é
gj(
ë
-
-- -----
)x,u =[
)x ,-
hk(
-
-- -----
]-a,aˉ ，设 ac = -a + aˉ
2 ，则称 ac ，ar 分别为区间数 a 的中点、半径。
由于存在不确定参数 u ，决策向量 x 所对应的目标
函数和约束函数不再是确定数，而变成区间数，在此，不
妨令：
fz(
gj(
hk(
其中：
-- -----fz(
)x = max
fz(
-
-- -----
u
-- -----gj(
)x = max
gj(
-
-- -----
u
-- -----hk(
)x = max
hk(
-
-- -----
u
由于 u 又可以写成：u = uc + [
)x,u
fz(
)x,u
gj(
hk(
)x,u
]
-1,1·ur 。假设 u 中
所有变量的不确定水平都较小，即 ur 非常小，因此对问
题（1）目标函数在 uc 处进行泰勒一阶展开：
-- -----f2(
)x = min
u
)x = min
u
)x = min
u
)x,u ,-
)x,u ,-
)x,u ,-
fz(
gj(
hk(
)
)x ,⋯,
)x ,-
F(
f2(
-
-- -----
min
x
)x,u =((
)x ,-
f1(
-
-- -----
(
)x ,-
fz(
-
-- -----
)
)x ,(
-- -----f1(
)
)
-- -----fz(
)x
（3）
（2）
其中：
p
)
)
ur
)x = fi(
|
x,uc - ∑
||
|
|
x,uc + ∑
||
|
fi(
- -- -----
- -- -----fi(
利用泰勒一阶展开，可以有效地将非线性函数转化
为线性形式，提高算法的运算效率。同理可仿照公式（3）
∂fi(
x,uc
∂ul
∂fi(
x,uc
∂ul
)x = fi(
l = 1
p
|
||
|
|
||
|
ur
l = 1
)
)
l
l
计算机工程与应用www.ceaj.org
陈志旺，黄兴旺，陈志兴，等：区间多目标优化非支配排序云模型算法
2017，53（22）
145
对约束函数做同样处理，综合公式（2）（3）可将公式（1）
整理如下：
Q:min
x
)
)x ,⋯,
-- -----f2(
F(
)x ,-
f2(
-
-- -----
)x,u =((
)
)x ,(
-- -----f1(
)x ,-
f1(
-
-- -----
)
)
(
-- -----fz(
)x ,-
)x
fz(
-
-- -----
-- -----gj(
)x ,-
aj,-aj ,j = 1,2,⋯,m
)x ≥ aj = é
ù
ù
ë
û-
û
]
)x = bk =[
]-
-- -----hk(
)x ,-
bk,-bk ,k = 1,2,⋯,n
x1,x2,⋯,xq ∈ X ⊂ Rq,
xi =[
]-
xi,-xi ,i = 1,2,⋯,q
u1,u2,⋯,up ⊂ R p,
ul =[
]-
ul ,-ul ,l = 1,2,⋯,p
)
)
gj(
s.t. é
ë
-
-- -----
[
hk(
-
-- -----
x = (
u = (
（4）
3 区间多目标优化基本概念
3.1 基于可能度的区间数比较
为了比较决策向量 xi 和 xj 的优劣性，设两决策向
量在第 z 维上的区间目标函数分别为：
]
xi ,u =[
xi ,u ,-
-
-
-
- ----- -
-fz(
)
)
)
fz(
xi ,u
- ----- -
-
-
-
-
-
-
-
-
xj ,u ,-
-fz(
- ----- -
)
)
)
fz(
xj ,u = é
ù
xj ,u
ë
û
-
-
-
-
-
- ----- -
fz(
fz(
由于区间数不能像确定数一样比较两个数的绝对
大小，故通过求解可能度来比较两个区间数之间的相对
大小关系，即区间比较关系，根据文献[12]给出的六种
位置关系可得：
)
fm(
x i,u <
-
-
-
-
-
- ----- --
-
)
fm(
xj,u <
-
-
-
-
-
- ----- --
-
m(
f c
)
P(
)
x i,u ≤ fm(
)
fm(
xj,u =
-
-
-
-
- ----- --
0,-
-fm(
)
)
fm(
ì
x i,u
xj,u ≤
ï
- ----- --
-
-
-
-
-
-
)
(
ï
-
-
-
-
-
-fm(
- ----- --
ï
2
)
)
fm(
xj,u -
x i,u
ï
ï
)
fm(
-
- ----- --
-
-
-
-
-
xj,u <
,
ï
)
m(
)
m(
ï
8 ⋅ f r
x i,u ∙f r
xj,u
-
-
-
-
-
- ----- --
-
ï
ï
-fm(
xj,u < -
-
- ----- --
-
-
-
-fm(
-
-
- ----- --
-
-
-
ï
)
)
ï
xi,u
ïï
)
)
fm(
x i,u
xj,u -
ï
ï
)
fm(
-
-
-
-
-
- ----- --
-
xi,u <
,
ï
ï
)
m(
2 ⋅ f r
x i,u
-
-
-
-
-
- ----- --
-
ï
ï
-fm(
xj,u < -
-
-
-
- ----- --
-
-fm(
-
-
- ----- --
-
-
-
ï
)
)
ï
xi,u
ï
í
-
-
- ----- --
-fm(
-
-
-
)
fm(
)
ö
æ
xi,u -
xj,u
ï
è
ø
)
fm(
ï
-
-
-
-
-
- ----- --
-
1 -
xi,u <
ï
,
)
m(
m(
)
8 ⋅ f r
xj,u
x i,u f r
-
-
-
-
-
- ----- --
-
ï
ï
ï
ï
-
-
-
- ----- --
-
-
-
-
-fm(
- ----- --
-
-
-
-
fm(
)
)
ï
xj,u
xi,u <
ï
ï
ï
)
)
m(
xj,u - f c
xi,u
ïï
)
fm(
xj,u <
,
ï
m(
)
ï
2f r
xj,u
-
-
-
- ----- --
-
-
-
ï
ï
-fm(
- ----- --
-
-
-
-
-
-
xi,u < -
-
-
- ----- --
-
-fm(
ï
)
)
ï
xj,u
ï
ï
-
-
-
- ----- --
-
-
-fm(
)
fm(
)
ï
xi,u ≤
xj,u
1,
î
-
-
-
-
-
- ----- --
-
其中，P(
)
)
x i,u ≤ fz(
xj,u 表示区间 fz(
fz(
)
于区间 fz(
xj,u 的可能度。
fm(
)
)
fm(
x i,u <
-
-
-
-
-
- ----- --
-
（5）
)
fm(
xj,u <
-
-
-
-
-
- ----- --
-
3.2 基于可能度的占优关系
x i,u ≤ fz(
fz(
)
若可能度 P(
)
)
就称区间 fz(
或者区间 fz(
)
)
xj,u ≥ σ, σ ∈ [
x i,u 在区间意义 σ 下小于等于 fz(
xj,u 在区间意义下 σ 大于等于 fz(
]
0.5,1 时，
)
xj,u ；
x i,u 。
x1,u 均在区间意义
x1,u 在区间意义 σ 下
x2,u ，则称 x1 以 P 占优 x2（P 代表区间数
)
)
)
∂ 下小于等于 fi(
小于等于 fi(
之间的区间比较关系），记为 x1 ≻ P x2 ，即：
x2,u 且存在 fi(
)
)
由文献[12]可知如果所有的 fi(
x1 ≻ P x2 ⇔ ∀i ∈ (
1,2,⋯,z , ∍ :
)
P( fz(xi,u) ≤ fz(xj,u)) ≥ ∂
∃i ∈ (
∂,σ ∈ [
1,2,⋯,z , ∍ :P( fz(xi,u) ≤ fz(xj,u)) > σ
]
0.5,1
)
（6）
公式（6）虽然可以得到区间数之间的占优关系，但
其占优结果会随着 ∂ 和 σ 取值的变化而不同，在此不妨
设问题（1）中有 2 个目标函数，图 1 展示了 4 个解对应目
标空间的值在直角坐标轴上的分布情况。
f2
3
1
4
2
O
f1
图 1 区间数之间的占优关系
由图 1 可知，矩形 1，3 在 f1 方向相等，矩形 2，4 同样
在 f1 上相同，矩形 1，4 在 f2 方向相等。若当 ∂ > 0.5 ，由
公式（6）可知图中 4 个矩形都没有占优关系，但实际上，
从图中可以看出，矩形 1 和矩形 2 比矩形 3 和矩形 4 更靠
近原点方向，因此矩形 1、2 应该优于矩形 3、4，因此对公
式作如下改进：
)
)
)
定义 2 如果所有的 fi(
x2,u 且存在 fi(
x1,u 均在区间意义 0.5 下小
x1,u 在区间意义 0.5 下小于
x2,u ，则称 x1 以 P 占优 x2（P 代表区间数之间的区
于等于 fi(
fi(
间比较关系），记为 x1 ≻ P x2 ，即
)
x1 ≻ P x2 ⇔ ∀i ∈ (
)
1,2,⋯,z , ∍ :
P( fz(xi,u) ≤ fz(xj,u)) ≥ 0.5
∃i ∈ (
)
1,2,⋯,z , ∍ :P( fz(xi,u) < fz(xj,u)) > 0.5（7）
定义 3 如果 x1 不以 P 占优 x2 ，且 x2 也不以 P 占优
x1 ，则称 x1 和 x2 以 P 互不占优，记为 x1||P x2 。
x i,u 小于等
)
定义 4 对于公式（4）中所描述的优化问题，如果对
于 x ∈ X ，不存在 x* ∈ X ，使得 x* ≻ P X ，则称 x 为公
式（4）所描述问题的 Pareto 最优解，简称 Pareto 最优解。
定义 5 根据文献[7]中的两区间之间距离公式为：
计算机工程与应用www.ceaj.org
146
2017，53（22）
Computer Engineering and Applications 计算机工程与应用
d[
fz(
xi,u ,fz(
)
(
xi,u ⋂ fz(
其 中 ：D = f c
T = fz(
的交集，T r 为区间 T 的半径。
xi,u - f c
xj,u 表示区间 fz(
)
)
z
(
)T r 2
]
)
(
xj,u = D2 + 1
)
3 F - 2
3
(
xi,u
xj,u , F = f r
)
)
z
)
2 + f r
(
xi,u 和区间 fz(
)
xj,u 2,
)
xj,u
z
z
（8）
当区间数变成确定数时，公式（8）即退化成普通数
轴上两点间的距离，因此，该公式不仅可以计算区间数
之间的距离也可以计算确定数之间的距离。
定义 6 目标函数为区间数的拥挤距离如下：具有相
同序值的云团中个体 i 周围的个体 i - 1 与 i + 1 区间距
离的 z 维欧几里德距离，记做 SDi 。
SDi = ∑
z d2(
m = 1
fm(
xi - 1,u ,fm(
)
xi + 1,u
)
)
（9）
4 约束条件的处理
)x ,-
bk ≤[
hk(
-
-- -----
由文献[12]可知约束条件会把决策空间分成可行
解区域和不可行解区域，而最优解集必然在可行解区
域。从公式（4）可以看出约束条件有两种类型，分别为
等式约束和不等式约束，对于等式约束，可以牺牲某些
准确性为代价，放宽约束而将它们转换成不等式约束，
为统一格式，本文把所有不等式都转化为大于等于的形
式。例如，对于公式（4）中的等式约束 [
]
-- -----hk(
)x =
hk(
-
-- -----
]
[
]-
-- -----hk(
)x ,-
bk,-bk ，可以将其表示为 -
)x ≤ -bk ，进而可
以 将 其 表 示 为 两 个 不 等 式 约 束 -bk ≥[
]
-- -----hk(
)x 和
hk(
-
-- -----
[
hk(
bk 。因此公式（4）中 n 个等式约束转化
-
-- -----
为 2n 个不等式约束。考虑到公式（4）中还有 m 个不等
式约束，因此，公式（4）共有 2n + m 个不等式约束，令 ℓi
为 解 违 反 第 i 个 不 等 式 约 束 的 约 束 违 背 程 度 ，可 得
ℓi = 1 - P(
-bi ≥ hi(
)x,u ，则 ℓi 为：
P(
-bi ≤ hi(
ì
ïï
P(
hi(
í
ïï
P(
gi(
î
)
)
)x,u ≤ -
bi ,i = n + 1,n + 2,⋯,2n
)
)x,u ≤ -
ai ,i = 2n + 1,2n + 2,⋯,2n + m
)x,u ，即 ℓi = P(-bi ≤
)x,u ,i = 1,2,⋯,n
]
-- -----hk(
)x ≥ -
)x ,-
)x ,-
（10）
ℓi =
hi(
)
)
θmax(
)xq = max(
)ℓi ,i = 1,2,⋯,m + 2n
定 义 7 针 对 优 化 问 题（4），解 xq 的 约 束 违 背 度
)xq 为 xq 的约束违背程度 ℓi 中的最大值，即
θmax(
定义 8 针对公式（4）中所描述的优化问题，对于解
)xq ≤ θ ，则称 xq 为该优化问题的 Pareto 可
xq ，若 θmax(
行解，θ 称为约束允许违背度，需要人为给定，默认取值
为 0.5。
5 云模型基本概念
云模型是一种把语言概念转化为定量数据的不确
定转换模型，它主要反映客观事物或人类知识中概念的
两种不确定性：模糊性和随机性，并把两者完全集成在
一起，构成定性和定量的相互映射。
定义 9 设 U 是用数值表示的定量论域，C 是 U 上
的定性概念，若定量值 x ∈ U ，且 x 是定性概念 C 的一
]0,1 是有稳定
次随机实现，则 x 对 C 的确定度 μ(
倾向的随机数。若 U → [
)x ，则 x
在论域 U 上的分布称为云，记为云 C(
)x [13]，每一个 x
称为一个云滴。
]0,1 ，∀x ∈ U ，x ∈ μ(
)x ∈ [
定义 10 一维正态云算子 Arforward(
C(
Ex,En,He
)
)
[13]
)
)
x,μ(
)
x,μ(
En,He
)Ex,t
x - Ex 2/(
)2t2
)
是一个把定性概念的整体特征变换为定量表示的映射
π:C → cloud(
)x ，其中 Ex 为期望，En 为熵，He 为
超熵，cloud(
)x 满足下列条件：
t = Norm(
x = Norm(
)x = e-(
μ(
其中，Norm(
随机变量，由公式（11）~（13）得到的云滴 cloud(
即为定性概念的一次定量表示。
（13）
En,He 为期望为 En 、方差为 He 的正态
)
)x
（11）
（12）
x,μ(
)
Ex 是云滴在论域空间分布的期望，是最能够代表
定性概念的点，是概念量化的典型样本；熵 En 是定性
概念随机的度量，代表了这个定性概念随机性的度量；
超熵 He 是熵的不确定性度量，即熵的熵，主要代表了
云滴的离散程度。利用正态云算子，可把定性概念 C 转
变为数值表示的云滴集合，实现概念空间到数值空间的
转换。由文献[14]可知，随着熵的变大，云滴的范围也
在逐渐变大；随着超熵的变大，云滴的离散程度也在变
大，代表生成的子代云滴的稳定性变差，故超熵设置值
应该较小，关于超熵选取参考文献[14]。
由于目前的算法中，云团个体多是并行进化，即多
个云滴并行操作，为了提高算法的普适性，所以将一维
正态云算子推广至 m 正态云算子，具体算法如下：
（1）初始化表征定性概念 C 的三个数字特征，Ex =
{Ex1,Ex2,⋯,Exm}、En ={En1,En2,⋯,Enm} 和 He ={He1,
He2,⋯,Hem}以及云滴数 N 。
（2）生成以 Eni 为期望，Hei 为方差的正态随机数 ti
（公式（11））。
（3）生成以 Exi 为期望，En′i 为方差的正态随机数
xi（公式（12））。
（4）计算 μ(
)xi = e-(
xi - Exi
2/(
)
)2t 2
i （公式（13））。
6 NSCMA 算法
自然界生物通过自身的演化来适应周围的环境从
而不断地向前发展，进化算法就是基于这种思想逐步发
展起来的一类随机搜索技术。将云模型与遗传算法相
结合，遗传算法能够继承云模型中云滴的稳定性和随机
计算机工程与应用www.ceaj.org
陈志旺，黄兴旺，陈志兴，等：区间多目标优化非支配排序云模型算法
2017，53（22）
147
性特点，较好地克服了传统遗传算法中收敛速度慢及容
易早熟的不足。云模型在处理定性定量概念的转化方
面呈现出较好的特性，体现了良好的表达能力，针对云
模型这个特点，引出“父代周围的个体”这个概念，把云
滴当作父代，通过正向云算子（公式（11）~（13））生成子
代云团，云团中的大部分云滴集合在 Ex 周围，体现了
“龙生龙，凤生凤”的遗传特征，保证子代对父代优良特
性的遗传；同时控制熵的变化可以控制云团的范围，相
当于遗传算法中的交叉操作；控制超熵的变化可以控制
云团的离散程度，替代了遗传算法中变异操作，不同的
熵和超熵生成的云团不同，说明这是一个充满不确定性
的过程，是随机的和模糊的，体现了“一母生九子，九子
各不同”的变异特性。
因此本文在 NSGA-II 的基础上，用云模型的正态云
算子替代 NSGA-II 的遗传操作，提出非支配排序云模型
算法（Non-dominated Sorting Cloud Model Algorithm，
NSCMA），算法步骤如下：
（1）设云团规模即包含解的个数为 N ，初始化算法
k = 0 、En 和 He（其中 En =
He1,He2,⋯,Hem ）和约束允
总迭代次数 G、进化代数 k(
{
En1,En2,⋯,Enm 、He ={
许违背度 θ 。
}
}
)
（2）算出云团中满足约束条件的解数 No1 ，并记录
满足约束条件的解。
（3）从云团中随机选择一个云滴，作为父代，以这个
云滴为期望，通过二维正态云算子生成子代云滴。重复
这个过程，得到云团规模为 N 的子代云团，算出云团中
满足约束条件的解数 No2 ，并记录满足约束条件解。
（4）合并所有满足约束的解得到云团，判断 No1 +
No2 > N ，若不满足，返回步骤（3）继续求满足约束条件
解数 No2i ，设 i 为步骤（4）的循环次数，继续判断 No1 +
∑
n No2i > N ，直到满足条件进入第（5）步。
i = 1
（5）针对步骤（4）中满足约束条件的解，按照其中解
的序值和相同序值解的区间拥挤距离排序，并取前 N
个优势解，构成下一代云团 N ( )k 。
（6）从云团 N ( )k 随机选择一个云滴，通过二维正态
云算子（公式（11）~（13））生成子代云滴，重复第 5 章的
步骤 1~4 得到子代云团，去掉不满足约束条件的解得到
云团 Nw( )k 。合并 N ( )k 和 Nw( )k ，得到云团 W ( )k ，计
算云团 W ( )k 中解的序值（公式（7））和同序值解的拥挤
距离（公式（9））。
（7）针对云团 W ( )k ，根据精英策略[7]按照排序结果
选取前 N 个优势个体，构成下一代云团。
（8）判断算法是否迭代了 G 代，如果满足，输出最
优解，否则，令 k = k + 1 ，转到步骤（6）。
本文在步骤（4）中保留了可行解的同时对可行解数
目进行判断，若数目过少，则重新通过云算子生成可行
解进行补充，这样做不仅保证了可行解的数量，而且相
比于随机获得，补充解更利于云团的进化。
7 数值算例及讨论
本文以优化问题（14）[15]（15）[16]来验证算法的有效性。
Q1: min f1(
x1 + x2 - 7.5 2 +
)
]
0,0.3
（14）
2(
u2
f2(
s.t. g1(
g2(
x1 ∈ [
Q2: min f1(
)
)x,u = u1(
)
x2 - x1 + 3 2/4
2(
)
2(
)x,u = u2
x2 - 4 2/2
x1 - 1 /4 + u3
x1 - 2 3/2 + u2 x2 - 2.5 ≤ [
)
1(
)x,u = u2
)x,u = u3
1 x2 + u2
x1 - 3.85 -
x2 - x1 + 0.65 2 ≤ [
)
2(
8u2
]0,3 ,u1,u2 ∈ [
2 + x2 cos(
1 + x2
)
x1 - 2 2 + (
)
-5,10 ,u1,u2 ∈ [
]
0,0.3
]
0.9,1.1
)
u1πx1
x2 - 3 2 + x1 cos(
]0,5 ,x2 ∈ [
)x,u = x2
]
0.8,1.2
]
2
u2πx2
)x,u = (
f2(
x1,x2 ∈ [
)
（15）
为了减少随机性对算法的影响，以下的结果都是在
30 次实验差异不大的情况下给出的。若以下测试中不
特 殊 说 明 ，参 数 设 置 为 ：pop = 60 ，G = 100 ，θ = 0.5 ，
En = (
0.01,0.01 。为了衡量算法所得前
沿优劣，这里取文献[15]中的 E 测度（用于衡量前沿的
均匀性），D 测度（用于衡量前沿的散布度）和 C 测度
（用于衡量前沿的收敛性）。
7.1 算法参数的取值分析
0.3,0.2 ，He = (
)
)
表 1 为不同优化问题下进化代数对算法测度的影
响。对于优化问题 Q1 和 Q2，随着进化代数的不断增
大，Pareto 前沿的均匀性（ E 测度）和宽广性（ D 测度）
在不断变好，同时，算法的收敛性（C 测度）也在变好。
因此，对于本文算法来说，随着进化代数的增加，算法
Pareto 前沿的性能在逐渐变好。
Q1
优化问题
表 1 不同算例的进化代数 G 对算法性能的影响
C 测度
0.374 6
0.365 5
0.361 4
0.301 0
0.274 4
0.270 9
进化代数
G = 20
G = 50
G = 100
G = 20
G = 50
G = 100
D 测度
11.557 7
11.567 5
11.576 0
13.515 5
14.520 1
19.814 9
E 测度
0.255 9
0.160 4
0.143 8
0.364 6
0.307 9
0.292 5
Q2
由表 2 可知，对于优化问题 Q1 和 Q2 的测度都是随
着云团个体数独增加而逐渐变好。综上所述，随着进化
代数和云团的个体数的增加，Pareto 前沿性能是逐渐变
好的。
7.2 云模型参数分析
由表 3 可知，对于 3 个优化问题的决策变量 x1 ，随
着 En 减小，算法 Pareto 前沿的 E 测度在逐渐变好，其
他测度没有规律性的变化。由表 4 可知，随着 En 变小，
计算机工程与应用www.ceaj.org
148
2017，53（22）
Computer Engineering and Applications 计算机工程与应用
区间值
前沿中心
2.5
2.0
1.5
1.0
0.5
2
f
0
6
8
10 12 14 16 18 20 22
f1
（a）Q1 的 Pareto 前沿
2
f
14
12
10
8
6
4
2
0
－2
－4
区间值
前沿中心
0 2
4
6
8 10 12 14 16 18
f1
（b）Q2 的 Pareto 前沿
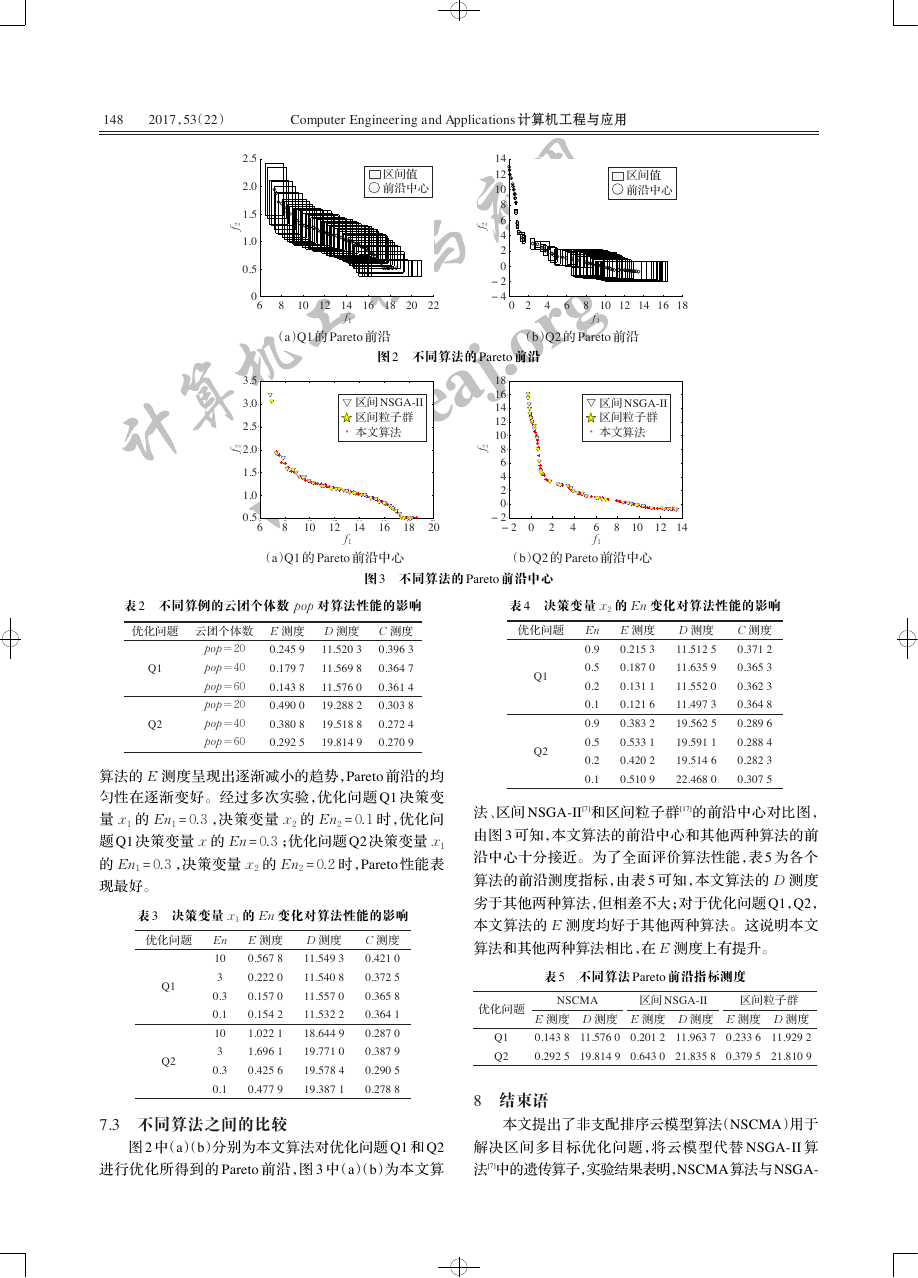
图 2 不同算法的 Pareto 前沿
2
f
3.5
3.0
2.5
2.0
1.5
1.0
0.5
6
区间 NSGA-II
区间粒子群
本文算法
8
10
12
f1
14
16
18
20
2
f
18
16
14
12
10
8
6
4
2
0
－2
－2
区间 NSGA-II
区间粒子群
本文算法
0
2
4
6
f1
8
10
12 14
（a）Q1 的 Pareto 前沿中心
（b）Q2 的 Pareto 前沿中心
图 3 不同算法的 Pareto 前沿中心
表 2 不同算例的云团个体数 pop 对算法性能的影响
优化问题
云团个体数
Q1
Q2
pop = 20
pop = 40
pop = 60
pop = 20
pop = 40
pop = 60
E 测度
0.245 9
0.179 7
0.143 8
0.490 0
0.380 8
0.292 5
D 测度
11.520 3
11.569 8
11.576 0
19.288 2
19.518 8
19.814 9
C 测度
0.396 3
0.364 7
0.361 4
0.303 8
0.272 4
0.270 9
算法的 E 测度呈现出逐渐减小的趋势，Pareto 前沿的均
匀性在逐渐变好。经过多次实验，优化问题 Q1 决策变
量 x1 的 En1 = 0.3 ，决策变量 x2 的 En2 = 0.1 时，优化问
题 Q1 决策变量 x 的 En = 0.3 ；优化问题 Q2 决策变量 x1
的 En1 = 0.3 ，决策变量 x2 的 En2 = 0.2 时，Pareto 性能表
现最好。
Q1
表 3 决策变量 x1 的 En 变化对算法性能的影响
C 测度
优化问题
0.421 0
0.372 5
0.365 8
0.364 1
0.287 0
0.387 9
0.290 5
0.278 8
D 测度
11.549 3
11.540 8
11.557 0
11.532 2
18.644 9
19.771 0
19.578 4
19.387 1
E 测度
0.567 8
0.222 0
0.157 0
0.154 2
1.022 1
1.696 1
0.425 6
0.477 9
En
10
3
0.3
0.1
10
3
0.3
0.1
Q2
Q1
表 4 决策变量 x2 的 En 变化对算法性能的影响
C 测度
优化问题
0.371 2
0.365 3
0.362 3
0.364 8
0.289 6
0.288 4
0.282 3
0.307 5
D 测度
11.512 5
11.635 9
11.552 0
11.497 3
19.562 5
19.591 1
19.514 6
22.468 0
E 测度
0.215 3
0.187 0
0.131 1
0.121 6
0.383 2
0.533 1
0.420 2
0.510 9
En
0.9
0.5
0.2
0.1
0.9
0.5
0.2
0.1
Q2
法、区间 NSGA-II[7]和区间粒子群[17]的前沿中心对比图，
由图 3 可知，本文算法的前沿中心和其他两种算法的前
沿中心十分接近。为了全面评价算法性能，表 5 为各个
算法的前沿测度指标，由表 5 可知，本文算法的 D 测度
劣于其他两种算法，但相差不大；对于优化问题 Q1，Q2，
本文算法的 E 测度均好于其他两种算法。这说明本文
算法和其他两种算法相比，在 E 测度上有提升。
表 5 不同算法 Pareto 前沿指标测度
优化问题
Q1
Q2
NSCMA
E 测度
0.143 8
0.292 5
D 测度
11.576 0
19.814 9
区间 NSGA-II
D 测度
11.963 7
21.835 8
E 测度
0.201 2
0.643 0
区间粒子群
E 测度
0.233 6
0.379 5
D 测度
11.929 2
21.810 9
8 结束语
7.3 不同算法之间的比较
图 2 中（a）（b）分别为本文算法对优化问题 Q1 和 Q2
进行优化所得到的 Pareto 前沿，图 3 中（a）（b）为本文算
本文提出了非支配排序云模型算法（NSCMA）用于
解决区间多目标优化问题，将云模型代替 NSGA-II 算
法[7]中的遗传算子，实验结果表明，NSCMA算法与NSGA-
计算机工程与应用www.ceaj.org681012141618200.511.522.533.5*681012141618200.511.522.533.5*-202468101214-2024681012141618*681012141618200.511.522.533.5*681012141618202200.511.522.5f1f2681012141618202200.511.522.5f1f2024681012141618-4-202468101214f1f2681012141618202200.511.522.5f1f2
陈志旺，黄兴旺，陈志兴，等：区间多目标优化非支配排序云模型算法
2017，53（22）
149
II 算法和粒子群算法相比，在 Pareto 前沿的均匀性上有
提高，并且通过云模型替代遗传操作，克服了 NSGA-II
交叉算子搜索性能较弱的缺点，提高了算法的收敛性。
云模型在表达的过程中，参数的选取影响着云滴的生
成，如何自适应地进行参数的选取，保证算法能更快地
收敛可以作为下一步的研究方向。
参考文献：
[1] 左兴权，王春露，赵新超 . 一种结合多目标免疫算法和线性
规划的双行设备布局方法[J]. 自动化学报，2015，41（3）：
528-540.
[2] Lu Shasha，Guan Xingliang，Zhou Min，et al.Land resourc-
es allocation strategies in an urban area involving uncer-
tainty：a case study of Suzhou，in the Yangtze River Del-
ta of China[J].Environmental Management，2014，53（5）：
894-912.
[3] Li Fangyi，Luo Zhen，Rong Jianhua，et al.Interval multi-
objective optimization of structures using adaptive Krig-
ing approximations[J].Computers & Structures，2013，119
（4）：68-84.
[4] Bhunia A K，Samanta S S.A study of
interval metric
and its application in multi- objective optimization with
interval objectives[J].Computers & Industrial Engineer-
ing，2014，74（1）：169-178.
[6] 王春 . 区间多目标知识引导进化优化方法研究[D]. 北京：
中国矿业大学，2014.
[7] 陈志旺，陈林 .求解约束多目标区间优化问题的改进 NSGA-
II[J]. 小型微型计算机系统，2014，35（11）：2502-2506.
[8] 郭凤鸣 . 基于云模型的遗传进化算法的研究[D]. 南京：南
京理工大学，2013.
[9] 许波，彭志平，余建平，等 . 基于云模型的 NSGA-II 算法改
进[J]. 小型微型计算机系统，2012，33（7）：1599-1602.
[10] 彭建刚，刘明周，张铭鑫，等 . 基于改进非支配排序的云模
型进化多目标柔性作业车间调度[J]. 机械工程学报，2014，
50（12）：198-205.
[11] Wang Guoyin，Xu Changlin，Li Deyi.Generic normal
cloud model[J].Information Sciences，2014，280：1-15.
[12] 姜潮 . 基于区间的不确定性优化理论与算法[D]. 长沙：湖
南大学，2008：13-24.
[13] 张光卫，何锐，刘禹，等 . 基于云模型的进化算法[J]. 计算
机学报，2008，31（7）：1082-1091.
[14] 刘禹，李德毅，张光卫，等 . 云模型雾化特性及在进化算法
中的应用[J]. 电子学报，2009，37（8）：1651-1658.
[15] 陈志旺，白锌，杨七，等 . 区间多目标优化中决策空间约
束、支配及同序解筛选策略[J]. 自动化学报，2015，41（12）：
2115-2124.
[16] 白锌 . 昂贵区间多目标优化数据挖掘求解策略[D]. 秦皇
岛：燕山大学，2015.
[5] 郑玉蒙 . 区间多目标规划问题的优化方法及应用研究[D].
[17] 张勇，巩敦卫，郝国生，等 . 含区间参数多目标系统的微粒
保定：河北大学，2015.
群优化算法[J]. 自动化学报，2008，34（8）：921-928.
（上接 120 页）
[6] Maruf S O，Azhar M U，Khawaja S G，et al.Crackle
separation and classification from normal Respiratory
sounds using Gaussian Mixture Model[C]//International
Conference on Industrial and Information Systems，2015.
[7] Daubechies I，Heil C.Ten lectures on wavelets[J].Comput-
ers in Physics，1992，93（3）：1671-1671.
[8] Tenenbaum J B，De S V，Langford J C.A global geomet-
ric framework for nonlinear dimensionality reduction[J].
Science，2000，290（5500）：2319-2323.
[9] Belkin M，Niyogi P.Laplacian eigenmaps and spectral tech-
niques for embedding and clustering[J].Advances in Neu-
ral Information Processing Systems，2002，14（6）：585-591.
[10] Roweis S T，Saul L K.Nonlinear dimensionality reduc-
tion by locally linear embedding[J].Science，2000，290
（5500）：2323-2326.
[11] Liu X Z，Yuen P C，Feng G C，et al.Learning kernel
in kernel-based LDA for face recognition under illumi-
nation variations[J].IEEE Signal Processing Letters，2009，
16（12）：1019-1022.
[12] Mallat S G.A theory for multiresolution signal decom-
position：the wavelet
representation[J].IEEE Transactions
on Pattern Analysis & Machine Intelligence，1989，11
（7）：674-693.
[13] 崔振，山世光，陈熙霖 . 结构化稀疏线性判别分析[J]. 计算
机研究与发展，2014，51（10）：2295-2301.
[14] Mallat S.A wavelet
tour of signal processing，third edi-
tion：the sparse way[M].[S.l.]：Academic Press，2008.
[15] Hadjileontiadis L J，Panas S M.A wavelet-based reduc-
tion of heart sound noise from lung sounds[J].Interna-
Informatics，1998，52（1/3）：
tional Journal of Medical
183-190.
[16] Abbasi S，Derakhshanfar R，Abbasi A，et al.Classifica-
tion of normal and abnormal
lung sounds using neural
network and support vector machines[C]//Iranian Con-
ference on Electrical Engineering，2013：1-4.
计算机工程与应用www.ceaj.org
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
