过驱动航天器推力器动态控制分配方法.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 过驱动航天器推力器动态控制分配方法# 陈寅欣，张世杰，唐生勇* （哈尔滨工业大学卫星技术研究所，哈尔滨 150080）摘要：针对推力器冗余配置的过驱动航天器，在建立推力动态分配数学模型基础上，提出了一种基于零空间的控制分配修正伪逆法，该方法通过计算效率矩阵的零空间向量及其修正参数实现对不满足推力器约束的初解修正，给出满足约束要求的推力器分配结果。并探讨了推力动态分配的修正伪逆法在航天器轨道姿态一体化控制问题中的应用，解决了轨道姿态一体化控制过程中期望控制力/力矩动态分配问题。最后，通过数学仿真验证了所提出的动态推力分配算法的有效性。该研究为实现推力器的姿控和轨控共用、有效降低控制任务的燃料消耗提供了一条可行技术途径。关键词：航天器；推力器；控制分配；伪逆法；零空间中图分类号：V448.2 Dynamic Thruster Allocation for Overactuated Spacecraft CHEN Yinxin, ZHANG Shijie, TANG Shengyong (Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150080) Abstract: For the overactuated spacecraft equipped redundant thrusters, a null-space-based redistributed pseudoinverse algorithm is proposed based on the thruster allocation model. The proposed algorithm modified the initial solution, which may lead the thrusts into saturation, by analyzing the null-space of the control effectiveness matrix, and revises all the thrusts to the confine that thrusters could offer. the proposed allocation method is used to integrated attitude and orbit control problem for desired control force and torque distribution. Finally, mathematical simulations are conducted, the results validate the feasibility and effectiveness of the proposed allocation algorithms. A feasible approach is provided for the realization of thruster-shared by attitude control and orbit control, and fuel consumption reduction. Keywords:Spacecraft; thruster; control allocation; pseudoinverse; null space 0 引言航天器控制是使其沿预定轨道运行或保持特定姿态指向的过程，是完成航天任务的重要前提，控制算法设计一直是航天领域的研究热点，但传统控制算法输出是期望的控制力/力矩，而非执行机构所需要控制指令，要完成航天器控制还需将期望控制量在执行机构间加以分配。为确保航天器在轨可靠运行，通常采用执行机构硬件冗余的备份方案，在此情况下控制量分配方案并不唯一，特别是在需要考虑期望控制量的最优分配、执行机构故障动态隔离 5 10 15 20 25 30 与系统的动态重构等情况下，使得期望控制量分配问题更为复杂，采用预先制定分配列表等传统方式已难以满足上述需求，需探索能满足在轨动态分配的新方法[1~3]。 35 动态控制分配方法(Dynamic Control Allocation)是由控制算法给出的期望控制量出发，在各类型约束条件和最优目标下，实时地将期望控制量在冗余配置的执行机构间进行分配，使执行机构实际控制输出尽可能与期望控制相吻合的一种控制设计技术。在执行机构存在冗余 40 的条件下，动态控制分配方法可以实现某一优化准则或约束下的优化分配，提高系统对执行机构故障的容错能力[4,5]，为航天器推力器动态分配问题提供了一条可行、有效的解决途径。控制分配问题本质上是一个在约束条件下从期望控制量到各个执行机构控制指令的非线性映射过程。广义的控制分配问题数学上就是要求解不确定的系统方程，特别是典型的约基金项目：高等学校博士学科点专项基金（20070213068）作者简介：陈寅欣，(1986-)，男，硕士研究生，主要研究方向：过驱动航天器控制系统设计. E-mail: chenyinxin403@163.com - 1 -

45 50 55 60 65 70 75 中国科技论文在线 http://www.paper.edu.cn 束方程。控制分配算法输入是控制算法输出的期望控制目标 ( ) 是被控系统的实际控制输入 ( ) g t 得到线性关系式 ( ) υ ，式中， B 为 k m× 的控制效率矩阵，且有 t= ( ) ℜ → ℜ t ∈ℜ t ∈ℜ Bu |m u υ : m k k ，其中 m k> 。给定 ( )tυ ，存在映射 ( ( )) t 是被控系统实际的控制输入到期望控制作用的映射。如果只考虑线性情况可以，控制分配算法输出 υ ， t= ( ) g u rank ( k=B ) 。迄今为止已结合实际提出了多种控制分配算法，可归纳为主要两大类：非优化分配法和优化分配法。非优化控制分配方法主要有直接几何法、链式分配法(Daisy chaining)、饱和分配以及混合分配法；基于约束优化的控制分配算法是将控制分配问题转化为约束优化问题，主要有广义逆法、基于数学规划方法的控制分配等算法[6,7]。动态控制分配方法在航天器控制领域的应用是一个相对崭新的问题，面临多目标、多约束等诸多困难，因此如何引入其他领域研究相对较多的动态控制分配理论和方法，设计适合航天器及其编队的动态控制分配算法，是一个有必要也值得深入研究的课题。本论文将针对推力器冗余配置情况，探索适应航天器推力动态分配问题特点的控制分配方法，并研究在航天器轨道姿态一体化控制问题中的应用，探索推力控制分配算法用于解决以推力器为执行机构的冗余航天器的控制问题的可行性。期望通过本论文的研究工作，确保航天器控制性能和燃料(能源)消耗等指标最优，增强对推力器故障的容错能力和系统重构能力，进而提高航天器智能自主运行能力，将具有重要的理论研究意义和工程应用价值。 1 推力分配问题的数学模型推力分配(Thrust Allocation)问题是将卫星控制算法给出的期望控制量在冗余配置的推力器之间进行动态分配的控制技术，本文重点针对推力分配问题进行研究。首先建立推力分配问题数学模型，在分析该模型基础上，设计合适的分配算法。设有 n 个推力器，安装于航天器固联坐标系 b =e 安装位置矢量矩阵为[ x y z , d d , d ] ) , , b b Ox y z (坐标轴与航天器惯性主轴重合)，其 r v 表示由航天器质心指向第 i 个推力器 d e i i i Τ i 2 1 , dL ， ( = ] x y z Τ , n i i 的位置矢量，而 [ =d 的三个基矢。推力器产生的单位推力矢量矩阵为[ 则表示 idv 在 b , b b i i i e e 2, 1 , e v ⎡ = ⎣ eL 。式中 ie , n ] Ox y z 三轴上的分量大小， e e e , x , y Τ ⎤ ⎦ z 为体系 i i i i ) e sin cos ,sin ,cos α β α β α i ( =e cos i Τ=e e ev v 为第 i 个推力器的单位推力在 b i i [ =ev cos i 为第 i 个推力器产生的单位推力在体坐标系三轴上的分量。设第 i 个推力器推力大小为 ( iF i 推力，则它对航天器质心的推力为： ] α β α β α Τ 1,2, = L ，且 0 F F i i ,cos ,sin cos sin b b ≤ n ) , i i i i i Ox y z 三轴上的分量。 u ≤ ， u iF 为第 i 个推力器的最大 i iF=U ev i 其产生绕质心的作用力矩为： T i v d i iF e v i = × ( ) 设所有推力器的推力组成的列阵为 =F [ F F 1 2 , , L , ] F Τ n ，则其相对航天器质心的作用力矩可表示为： - 2 -

中国科技论文在线 http://www.paper.edu.cn T = ∑ ∑ T i = ( v d i × ) e F AF v i = i (1) n i 1 = n i 1 = 所产生的作用力可表示为： 80 U = n ∑ ∑ U = i n i 1 = i 1 = F i e BF v i = (2) 式中， A 为所有推力器单位推力矢量相对航天器质心的力矩矩阵： A × , , L v d n e v n ⎤ ⎦ (3) = = v d ⎡ × ⎣ 1 [ a a , 1 v e d v , × 1 2 a , , L n 2 e v 2 ] B 为所有推力器单位推力矢量作用于航天器的推力矩阵： v v B e e , 1 2 b b , 1 2 (4) , L , v e n b n = = ] ] [ [ , , L 0 i = 注意到 A 与 B 中元素存在着一定联系： a b T i 式中， ia 为 A 的第 i 列， ib 为 B 的第 i 列。式(1)至式(4)构成推力分配问题的数学模型。 2 推力分配算法本论文要研究的推力器分配算法的实质是一个在约束条件下从期望控制量到各个执行身的特性。航天器上的推力器实际的推力输出是具有下限为零，上限为力量，而且推力器的输出是一个开关量，即关闭时推力输出是零，工作时输出最大值 u 机构控制指令的非线性映射过程。所研究的分配方法是针对推力器的，故需要考虑推力器本 uF 的推力阈值的推 iF 。这种非线性的特点将给分配算法的建立造成极大困难，故本论文需要假设推力器的输出是一个 0 ⎡ ⎣ ⎤ ⎦ 的线性输出量，这样可以将算法以线性系统来设计，简化设计难度，但是最后需 iF u i 85 90 95 要加入调制解调过程。航天器在轨运行时，由于实时性的要求，希望提高解算速度。因此考虑以伪逆法为基础建立分配算法，伪逆法虽然有计算快，所用控制量小的有点，但是单纯的伪逆法没有考虑推力器推力受限的因素，所以结果出现负向推力，而本论文中选用单向推力器为研究对象，单 100 向推力器无法输出负向推力。为了解决这个问题，再引入链式递增法则将伪逆法的初始解修正到推力器修正到推力器能够提供的推力器范围内，这种方法既解决了推力器推力受限的问题，又保留了伪逆法的计算快的优点。 2.1 伪逆方法寻求初始解考虑泛函： 105 J ( =∑F ) F i = 2 n i 1 = T F F (5) 求得的 F 应该满足其所有元素的平方和最小。考虑到产生的推力必须满足轨道和姿态的控制要求，即满足约束条件： C = DF (6) 利用 Lagrange 乘子法求解，令乘子为 [ =λ λ λ 1 2 L λ n ]T - 3 - ，定义标量函数 ( H F λ ， , )

中国科技论文在线 http://www.paper.edu.cn 引出新的泛函： 1 2 = F λ , ) H = ( T T ( F D DD F D DD ) T = ( ( )− T ⇒ 式中 T ) 1 − − 1 C C D C = + D DD —— D 的伪逆。 T 1 T F F λ C DF (7) + − ( ) T (8) 110 115 120 125 130 利用伪逆方法求取的推力器能够满足航天器姿态控制要求，但其存在一定的缺陷，亦不能保证求得的推力在推力器所能提供的推力大小范围内，比如出现负向推力输出，这不符合单方向推力器的特性，这就需要对其进行修正，修正分配量中的负向推力输出。或是推力超出推力器最大推力，这也使得推力器无法输出。 2.2 基于零空间的修正伪逆法本节引入控制效率矩阵零空间的概念，对伪逆法所产生的初始解，利用控制效率控制零空间的特性进行解的线性叠加，使超出推力器阈值的解重新落入推力器的控制子空间，并使分配所得的解满足二次线性规划的优化指标。首先给出控制效率矩阵零空间的概念。定义 2.1：设 nF 是向量在 x 控制效率矩阵的映射下所形成的像的集合，那么所有被 D 映射成为零向量的向量 x 组成的集合 nF 称为控制效率阵 D 的零空间，即： D : nR R n→ ( 6 > 6) n = = R } F n x Dx ½ ( (9) x 0 ∈ ) 6 ,那么 nF 是由 n-6 个列向量构成的正交基张成。该正交基通过式 =D { rank 由于，求出零空间 nF 。设 nF 的正交基为 ξ ，则 nF 为： 0 [ = (10) ] 6 , ξ ξ n 2 ξ L ξ 1 n =DF F i R ∈ n 零空间的任意向量可表示为： x K ξ K ξ 2 2 K K 1 1 1 =K K ξ + [ n − K 6 n 6 − L = + + ] Τ − n 式中由线性代数定理可知：若 η 是非齐次线性方程组的解， ξ 是齐次线性方程组(导出组) L 6n − 2 (11) n i R = F K ξ n = ， iK 为任意实数。的解，则 = + x η ξ 还是非齐次线性方程组的解。因此，基于零空间概念可对伪逆法进行修正使其满足某种要求。 135 2.2.1 基于零空间的修正伪逆算法在介绍设计伪逆修正策略之前，先给出一重要定理：定理 2.1： ]T 0 T U ， [ ; ∃ ≥F 使 =C DF 的充分必要条件是： D 行满秩且 =D A B 。 ]T ; 里 [ =C >F n∃ 0, 使 n =DF 0 ，这证明 ⇒ 如果力和力矩在空间中任意取值且 =C DF ，则 D 必须行满秩；现取 0 0 0 F D C 0 + + T T 1 − D DD 为矩阵 D 的伪逆(the ( ) >F n∃ ，则只要γ取得足够大， 0 - 4 -

中国科技论文在线 http://www.paper.edu.cn 就可以满足 0≥F ，这里取 γ ≥ max ( n i 1, , = L −D C + ) /i F ni 。定理 1 中的C 为推力分配的期望量， D 为航天器系统效率矩阵， nF 为零向量空间，故 145 结合零空间概念，令修正的伪逆解可以做如下修正： + n pc = + + = x DD C F K (12) F F 等式(12)两端同时左乘 D ，由定理 2.1 可知 DF DD C DF K DD C 可见加上 nF K 项后，并不影响推力完成克服力和力矩的工作，故只要 K 选取得当，就可以将伪逆解重新落入执行器的控制子空间。下节中将结合零空间概念，设计参数 K 解决负向伪逆解的问题。 K C (13) = + = + = 0 n + + 150 2.2.2 参数 K 的求解零空间的引入使期望转矩得到了有效地分配。为了满足系统的实时性的要求，在对期望向量进行实时分配时，需要快速地找到一个向量 K 使伪逆初解重新落入控制子空间。下面将结合链式分配法的思想给出一种求解参数 K 的方法： 155 首先，需要对伪逆初解 pcF 按照对应的推力器是否出现负值进行分块： F pc = F F ⎡ ⎢ ⎣ pc neg _ pc pos _ ⎤ ⎥ ⎦ , F pc neg _ < 0, F pc pos _ > 0 (14) 相应的，将零空间正交基 nF 按照对应的控制变量是否超出推力器下限极限进行分块： F n ⎡ = ⎢ ⎣ _ F n neg F n pos _ ⎤ ⎥ ⎦ (15) = F 所对应的零空 F 为 _pc pos 式中， _n negF 为 _pc neg 所对应的零空间正交基矩阵子阵， _n pos F 间正交基矩阵子阵。式(12)改写成： u F F n neg pc neg 1 _ u F F n pos 2 由于推力器的推力不能产生负值，因此将 1u 置于其推力器最小推力极限位置(本论文中设定为 0，若推力器有最小开关时间要求，可方便地设定为该约束)，于是由式(16a)可求得参数阵 K 为： K (16a) K (16b) pc pos + + = _ _ _ 160 165 170 (17) ( − F = = + n neg _ u 0 1 K F 相应地，控制变量 2u 修正为： u F 2 F n pos _ F + n neg _ pc pos pc neg F + = − ) _ _ ( ) (18) pc neg _ 最终的推力输出为： =F 其次由于星载推力器无法提供无限推力，其总会有一个最大推力极限，而式(18)仅考虑 (19) ]2 u 0 [ Τ 推力器下限问题，所以在下面，需要解决超推力上限的问题。 175 对于超上限问题，仍采用零空间思想进行修正。设定最大推力 u iF ，若式(19)的结果 2u 中 - 5 -

中国科技论文在线 http://www.paper.edu.cn iF 的分量，将 F 按照所对应的推力器是否超出推力上限进行调整并分块得：出现超过 u u ⎡ ⎢ u ⎢ ⎣ (20) ⎤ ⎥ ⎥ ⎦ u 2 F F u u ' 3 ' 4 = > ≤ ⎡ ⎣ ⎤ ⎦ ⎡ ⎣ ⎤ ⎦ ' 4 ' 3 , u u , 将 3u 置于饱和位置 u u iF ， 3 ⎡ = ⎣ u F i L F Τ u ⎤ ⎦ i ，利用零空间思想，将零空间正交基 ' nF 按照所对应的控制变量是否超出推力上限也进行分块调整为： (21) 3 ⎤ ⎥ ⎦ F ' n ⎡ = ⎢ ⎣ F ' n F ' n 4 3nF 为 ' 式中， ' 3u 所对应的零空间正交基矩阵子阵， ' 4nF 为 ' 4u 所对应的零空间正交基矩阵 180 185 子阵。 ' = = + + u F K (22a) ' ' 3n 3 F K (22b) u ' ' 4n 4 那么可以写出： u 3 u 4 由于 3u 已经置于饱和推力，于是可以由式(22a)求得参数阵 'K 为： K ) u (23) ' 3 ( F u ' n 3 − = + 3 ' ' 同时将所得的参数阵 'K 代入式(22b) u 4 F F ' ' n n u ' 4 = + + 4 3 ) u (24) ' 3 190 最终的分配量为 u 3 Τ u 。 4 ] u 3 ( =F ' − [ 如果分配的结果出现了再次超限的情况，继续应用上述的方法经行多次修正，直到将控制分配量落入执行器的控制子空间内。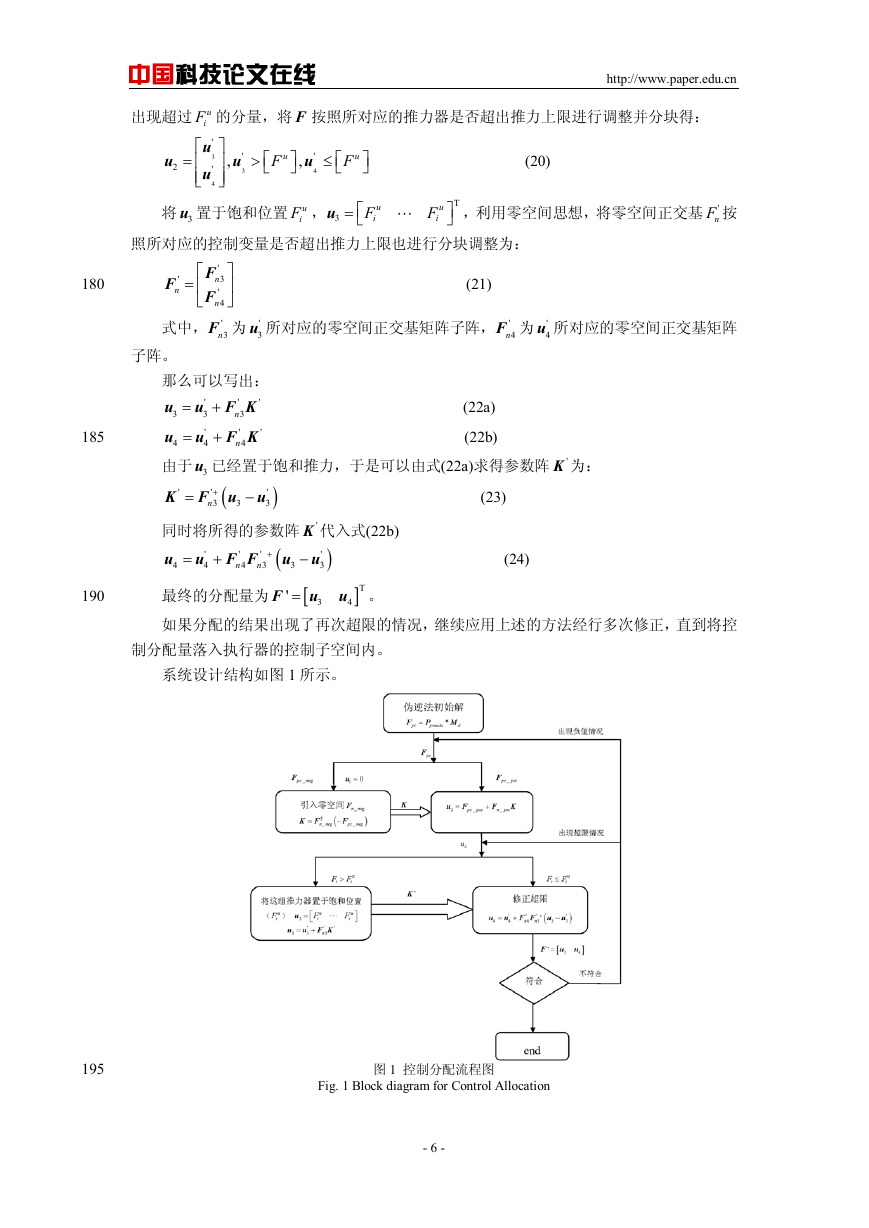系统设计结构如图 1 所示。 195 图 1 控制分配流程图 Fig. 1 Block diagram for Control Allocation - 6 -

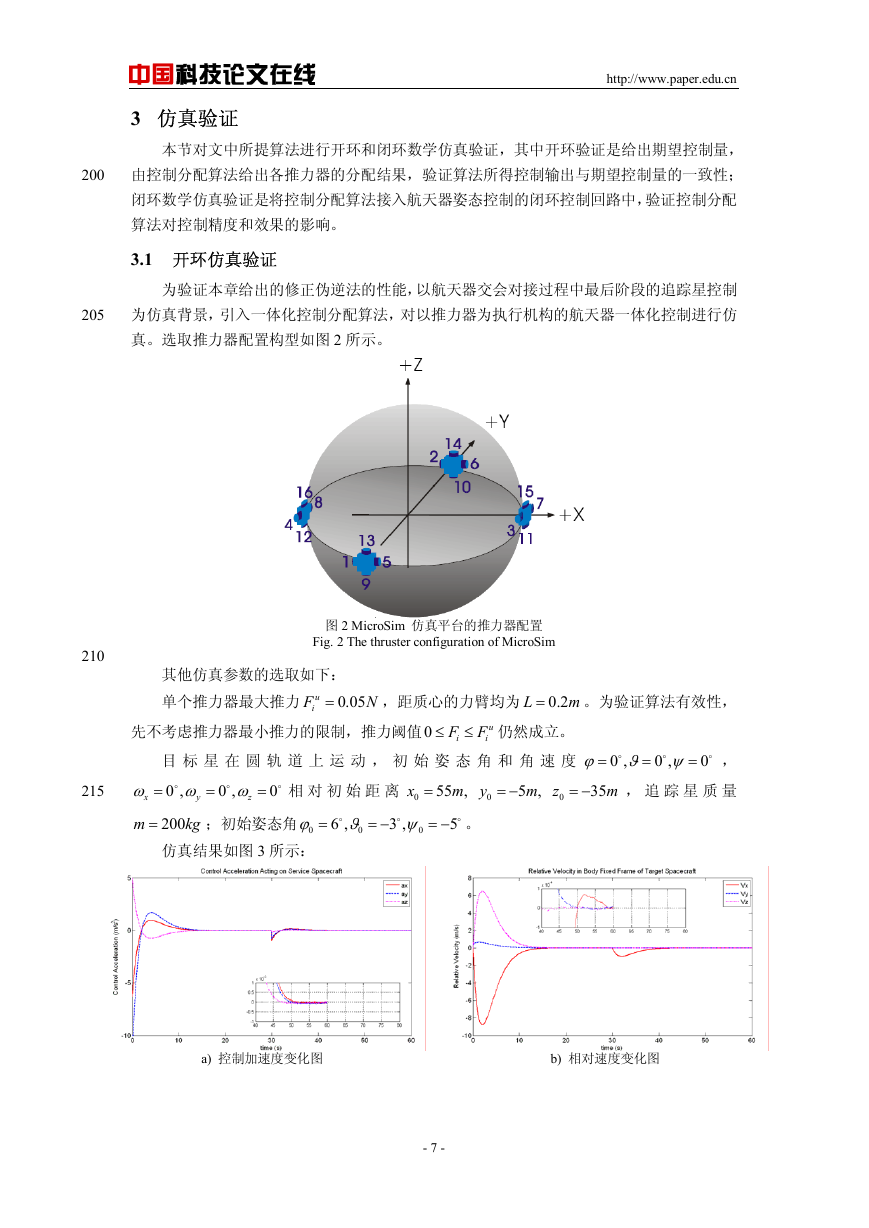
中国科技论文在线 3 仿真验证 http://www.paper.edu.cn 200 205 本节对文中所提算法进行开环和闭环数学仿真验证，其中开环验证是给出期望控制量，由控制分配算法给出各推力器的分配结果，验证算法所得控制输出与期望控制量的一致性；闭环数学仿真验证是将控制分配算法接入航天器姿态控制的闭环控制回路中，验证控制分配算法对控制精度和效果的影响。 3.1 开环仿真验证为验证本章给出的修正伪逆法的性能，以航天器交会对接过程中最后阶段的追踪星控制为仿真背景，引入一体化控制分配算法，对以推力器为执行机构的航天器一体化控制进行仿真。选取推力器配置构型如图 2 所示。 210 215 其他仿真参数的选取如下：单个推力器最大推力 u iF = 0.05 N 先不考虑推力器最小推力的限制，推力阈值0 ≤ 图 2 MicroSim 仿真平台的推力器配置 Fig. 2 The thruster configuration of MicroSim ，距质心的力臂均为 0.2 = L m ≤ 仍然成立。 u F F i i 。为验证算法有效性，目标星在圆轨道上运动，初始姿态角和角速度 0 , x o 相对初始距离 0 ω ω ω z m z 5 , 55 , m y 0 = − 0 , = = = = 0 0 o o o o = 0 , 0 , = ϕ ϑ ψ m 35 = − ，追踪星质量 = 0 o ， x m = y kg 200 = ；初始姿态角 0 仿真结果如图 3 所示： ϕ ϑ 0 6 , o = − 3 , o ψ 0 5 = − o 。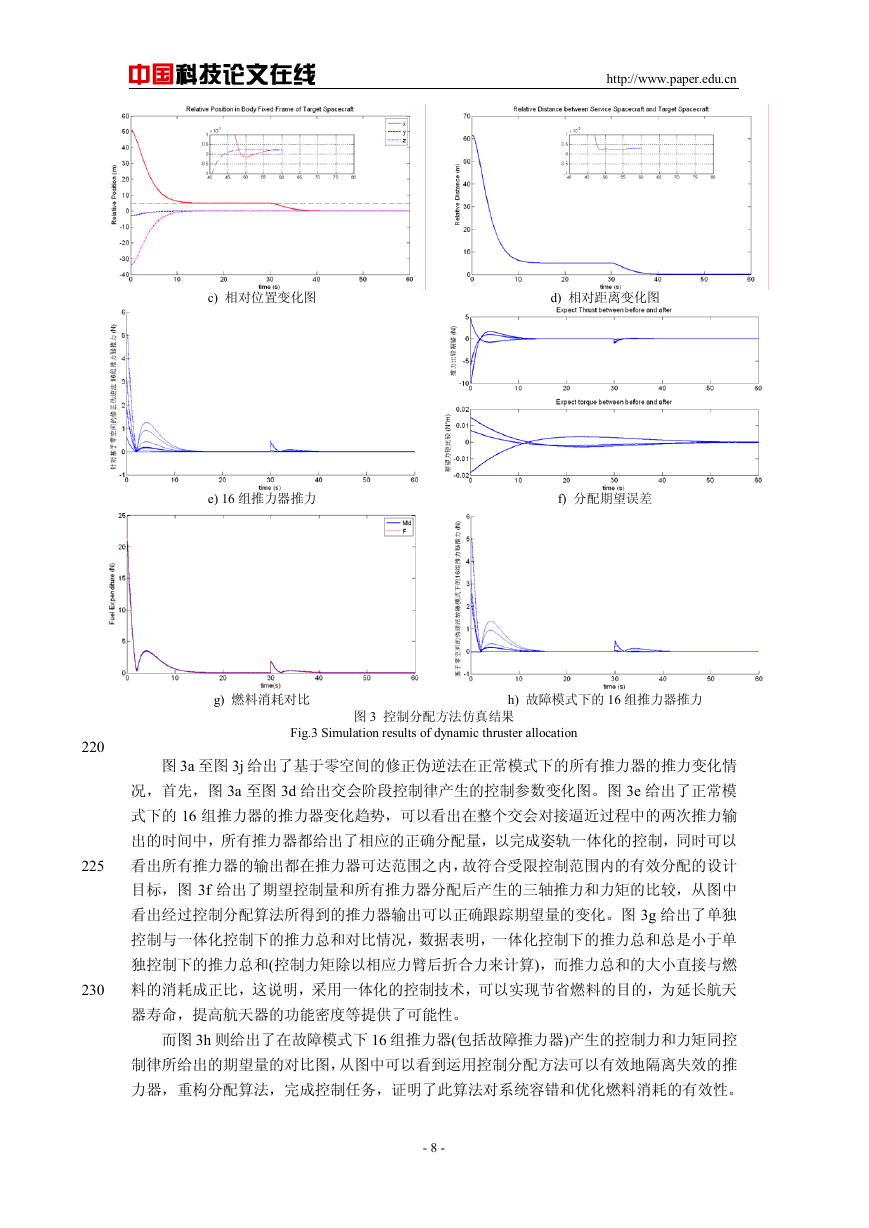 a) 控制加速度变化图 b) 相对速度变化图 - 7 -

中国科技论文在线 http://www.paper.edu.cn c) 相对位置变化图 d) 相对距离变化图 e) 16 组推力器推力 f) 分配期望误差 220 225 230 g) 燃料消耗对比 h) 故障模式下的 16 组推力器推力图 3 控制分配方法仿真结果 Fig.3 Simulation results of dynamic thruster allocation 图 3a 至图 3j 给出了基于零空间的修正伪逆法在正常模式下的所有推力器的推力变化情况，首先，图 3a 至图 3d 给出交会阶段控制律产生的控制参数变化图。图 3e 给出了正常模式下的 16 组推力器的推力器变化趋势，可以看出在整个交会对接逼近过程中的两次推力输出的时间中，所有推力器都给出了相应的正确分配量，以完成姿轨一体化的控制，同时可以看出所有推力器的输出都在推力器可达范围之内，故符合受限控制范围内的有效分配的设计目标，图 3f 给出了期望控制量和所有推力器分配后产生的三轴推力和力矩的比较，从图中看出经过控制分配算法所得到的推力器输出可以正确跟踪期望量的变化。图 3g 给出了单独控制与一体化控制下的推力总和对比情况，数据表明，一体化控制下的推力总和总是小于单独控制下的推力总和(控制力矩除以相应力臂后折合力来计算)，而推力总和的大小直接与燃料的消耗成正比，这说明，采用一体化的控制技术，可以实现节省燃料的目的，为延长航天器寿命，提高航天器的功能密度等提供了可能性。而图 3h 则给出了在故障模式下 16 组推力器(包括故障推力器)产生的控制力和力矩同控制律所给出的期望量的对比图，从图中可以看到运用控制分配方法可以有效地隔离失效的推力器，重构分配算法，完成控制任务，证明了此算法对系统容错和优化燃料消耗的有效性。 - 8 -

资料库

过驱动航天器推力器动态控制分配方法.pdf

相关推荐

开发技术

热门标签

最新资料