logo资料库

多孔介质微观结构的随机动力学构建方法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.61M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第33卷第9期 辽宁工程技术大学学报（自然科学版） 2014年9月 Vol.33 No.9 Journal of Liaoning Technical University（Natural Science） Sep. 2014 收稿日期：2014-01-08 基金项目：国家自然科学基金资助项目（51134005） 作者简介：张晓虎（1982-），男，河南 南阳人，博士研究生，主要从事岩石力学方面的研究. 通讯作者：何满潮（1956-），男，河南 灵宝人，博士，教授，主要从事深部岩石力学理论及工程方面的研究. 本文编校：杨 芳 文章编号：1008-0562(2014)09-1240-06 多孔介质微观结构的随机动力学构建方法 张晓虎1，何满潮1,2，刘得超1，任晓龙1 （1.中国矿业大学（北京） 力学与建筑工程学院，北京 100083； 2.深部岩体力学与地下工程国家重点实验室，北京 100083） 摘 要：针对多孔介质建模的复杂性，从随机动力学的朗之万方程出发，引入概率的影响，建立构造随机多孔介质的微观生长模型.通过不同的初始固相分布，该模型可以演化出各种不同性质的多孔介质微观结构.由于考虑了颗粒之间的作用力，模型生成的多孔介质与自然界真实的多孔介质更为接近，存在连通和不连通的孔隙结构，孔道迂回曲折.通过对多孔介质微观流动的数值模拟，验证该模型的实用性、可行性. 关键词：多孔介质；随机动力学；表征单元；微观结构；N-S方程 中图分类号：S 152.5 文献标志码：A Micro-model of porous media structure based on stochastic dynamic process ZHANG Xiaohu1, HE Manchao1, 2, LIU Dechao1, REN Xiaolong1 (1.School of Mechanics, Architecture and Civil Engineering, China University of Mining and Technology, Beijing 100083, China; 2.State Key Laboratory for GeoMechanics and Deep Underground Engineering, Beijing 100083, China) Abstract: This paper summarized and analysed the current researches on porous media structure modelling, and their advantages and disadvantages. A micro-model based on stochastic dynamic process was developed aiming at the difficulty of porous media’s micro-structure modelling. The Langevin equation was introduced along with probability. This model can get different kinds of micro-porous media structures in different initial solid distribution conditions. The model considers the interaction force between grains, so that the generated micro-model is quite similar to the real natural porous media structure, which contains tortuous porous structures connected or disconnected. An example of simulating the micro flow in porous media structure based this model is calculated, which validates the model’s feasibility and practicability. Key words: porous media; stochastic dynamic; representative element (RVE); micro-structure; N-S equations 0 引 言 多孔介质普遍存在于自然界之中，对多孔介质物理力学性质特性的研究具有非常广泛的工程应用前景，比如瓦斯控制、页岩气开发等等. 岩石就是一种典型的多孔介质[1].其内部孔隙的分布特征和拓扑结构直接影响着岩石的变形、强度以及渗流性质，而且在微观领域，这种影响更为直接. 由于多孔介质内部孔隙结构的复杂性，人们很难用几何的方法对其进行精确的描述，通常的方法是采用连续介质模型，但是这种方法只能反映材料的宏观性能，不能揭示材料的微观物理性质.建立合适的多孔介质模型便成为一种较为间接可行的研究微观多孔介质物理力学特性的方法. 学者们提出了多种多孔介质模型，大体上可以分为三类：概念模型、统计模型以及图像重构模型.在概念模型方面：Civan[2]建立了具有渗透壁的毛管模型，并推导出了更合理的孔隙度参数与渗透率之间的关系.李传亮[3]等采用球状颗粒模型阐述了岩石颗粒排列方式对孔隙度的影响以及颗粒粒径对比表面积的影响.邓彩华[4]等建立了一个二维DNS模型，研究了粒子的不同排列下多孔介质中流动阻力和压降. 在统计模型方面：Perrier和Lehmann[5-6] 同时考虑骨架颗粒度分布和空隙大小分布，并各自建立的多孔介质的统计分形模型.张东辉[7]将随机模拟方法应用于多孔介质中的物质传输过程，对不同孔隙通道连接率下的弥散规律进行了分析. 张东辉[8]利用分形结构（sierpinski地毯）计算了导热率与基中国煤炭期刊网 www.chinacaj.net
    第9期 张晓虎，等：多孔介质微观结构的随机动力学构建方法   1241质百分含量之间的关系.Wu[9]采用三阶马尔科夫网络建立了非均匀多孔介质模型，并计算了渗透率 . 袁锦越[10]采用分形几何学构建了多孔介质模型. Okabe和 Al-Kharusi[11-12]各自从多点统计模型中提取空隙网络，研究其渗流特征.鞠杨[13]通过砂岩CT图像获得了砂岩孔隙的几何特征及分布规律，构建了三维概率空隙结构模型. 在图像重构模型方面：Lin[14]以高分辨micro-CT图像为基础，建立了滤饼的三维空隙模型，并分析了滤饼孔喉分布的及连通性.Vogel[15]采用micro-CT 扫描图像重构模型，计算了烧结玻璃珠的毛管压力曲线.Okabe[16]综合了micro-CT 图像和二维薄片多点统计信息，建立了碳酸盐多孔介质模型.Talabi[17]从micro-CT图像中提取了填沙模型的孔隙网络.张挺[18]提出了一种基于多孔介质二维薄片图像和多点统计的多孔介质三维重构方法.王波[19]等利用马尔可夫链-蒙特卡洛方法重构了三维多孔介质模型.以上的研究方法广泛应用于不同的领域之中[20-27]. 以上三类建立模型的方法中，概念模型是一种抽象的简化模型虽然容易实现但无法反应真实多孔介质的各向异性和复杂性，统计模型相比概念模型更接近实际，能较好地反应材料的宏观平均性质，但无法反应真实微观结构的随机性和复杂性，将统计模型用于微观结构也是不合适的；基于图像重构的方法能够较好的体现多孔介质的真实面貌，但其建模和有限元计算过程较为复杂繁琐，不易实现.因此，本文从多孔介质中的表征体单元出发，将随机动力学的基本方程引入到多孔介质微观RVE结构的建模过程中来，建立了随机多孔介质的微观结构的RVE模型，并通过实例讨论了岩石微观结构对微观流动的影响. 1 多孔介质中的表征体单元 连续介质概念的本质乃是质点、或物理点、或在其上实行平均的表征性体积单元（简称为RVE），在使用宏观方法时，为构造给予连续介质理论的数学模型，需要在宏观水平上对围绕多空体某一点p的流体参数进行平均，进而用一定范围内的平均值去代替局部真值.平均容积尺寸与空隙率之间的关系见图1，可以看出对于非匀质多孔介质，选取的容积尺度不同，所获得的容积平均值也不同.如果选择的容积直径范围不合理，无法反应这一范围内的物理参数的真实值. 图1 平均容积尺寸与孔隙率的关系 Fig.1 relationship between size of RVE and porosity 要使表征体单元包含足够多的细观结构信息，从而使其能够代表多孔介质的统计平均性质，此表征体单元需满足如下条件： ① 此RVE单元应是绕p点的一个小范围，它远比整个流体区域要小； ② RVE单元应比单个空隙空间大得多，以致能包含足够多的空隙； ③ 在RVE中，其基本参数随空间坐标的变化幅度小，平均值逼近于真实值. 微尺度上的多孔介质中流体的流动发生在骨架空隙和缝隙之中，微尺度的方法更为直接地揭示了多孔介质的微观物理过程的本质和机理.通过对微观结构进行宏观的空间化平均，进而研究多孔介质中微观运动对宏观参数的影响，为此必须建立反映多孔介质结构特征的微观表征体单元，即多孔介质的微观RVE结构. 2 郎之万过程构造多孔介质微观结构 2.1 郎之万方程简介 根据随机动力学可知，朗之万方程为 ()Vmfftf ， （1） 式中，Vf为系统内部粒子之间的相互作用力；f为系统内部粒子运动所受到的运动方向相反的粘滞阻力；()t为系统内部粒子所受到的随机涨落力，它的数学期望为0. 2.2 含有两种粒子的郎之万过程 假设多孔介质是由固体颗粒和气体粒子两相共同构成的，以二维多孔介质为例，固相构成多孔L l平均容积的直径 均匀介质 大尺度非均匀介质01.0(x0) 中国煤炭期刊网 www.chinacaj.net
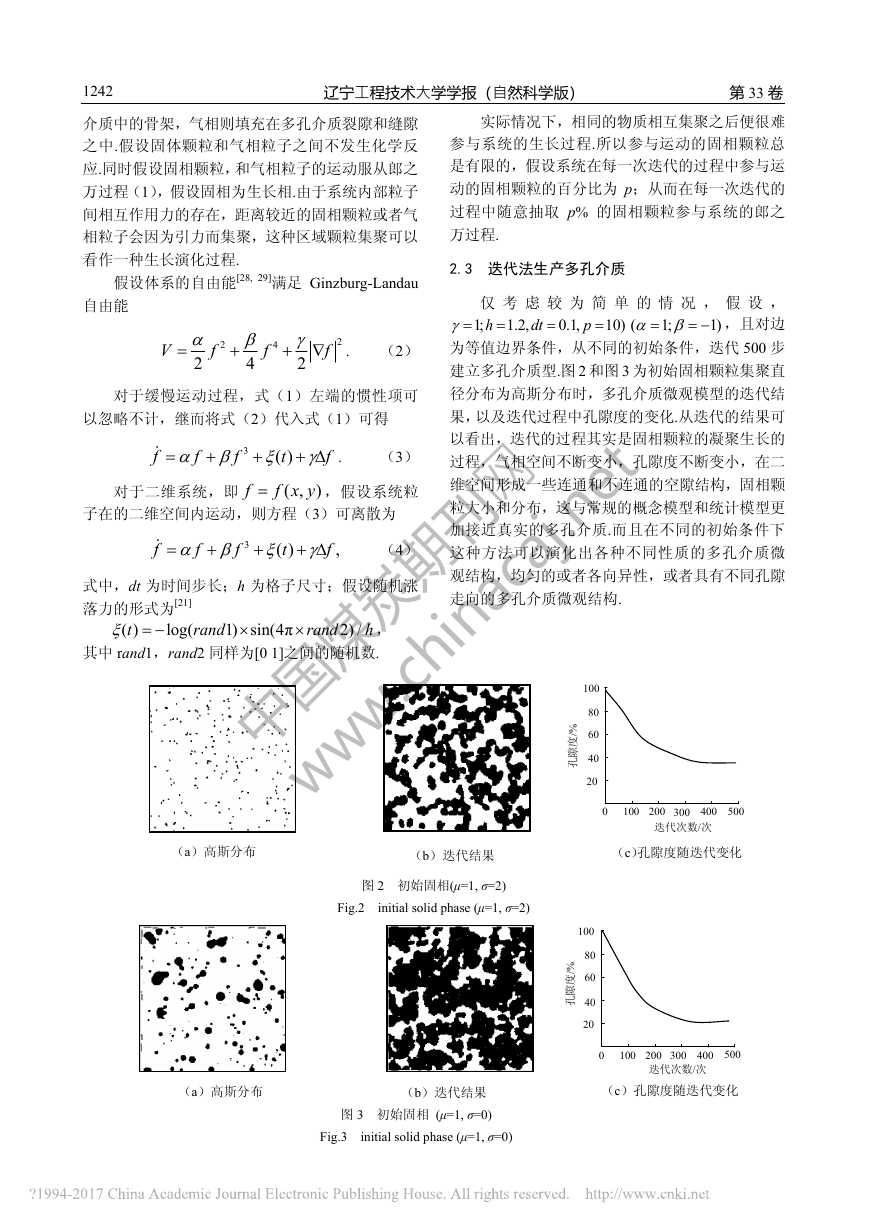
    辽宁工程技术大学学报（自然科学版） 第33卷  1242介质中的骨架，气相则填充在多孔介质裂隙和缝隙之中.假设固体颗粒和气相粒子之间不发生化学反应.同时假设固相颗粒，和气相粒子的运动服从郎之万过程（1），假设固相为生长相.由于系统内部粒子间相互作用力的存在，距离较近的固相颗粒或者气相粒子会因为引力而集聚，这种区域颗粒集聚可以看作一种生长演化过程. 假设体系的自由能[28, 29]满足Ginzburg-Landau自由能 224242Vfff. （2） 对于缓慢运动过程，式（1）左端的惯性项可以忽略不计，继而将式（2）代入式（1）可得 3()ffftf. （3） 对于二维系统，即(,)ffxy，假设系统粒子在的二维空间内运动，则方程（3）可离散为 3(),ffftf （4） 式中，dt为时间步长；h为格子尺寸；假设随机涨落力的形式为[21] ()log(1)sin(4π2)/trandrandh， 其中rand1，rand2同样为[0 1]之间的随机数. 实际情况下，相同的物质相互集聚之后便很难 参与系统的生长过程.所以参与运动的固相颗粒总是有限的，假设系统在每一次迭代的过程中参与运动的固相颗粒的百分比为p；从而在每一次迭代的过程中随意抽取p% 的固相颗粒参与系统的郎之万过程. 2.3 迭代法生产多孔介质 仅考虑较为简单的情况，假设，1;1.2,0.1,10)hdtp(1;1)，且对边为等值边界条件，从不同的初始条件，迭代500步建立多孔介质型.图2和图3为初始固相颗粒集聚直径分布为高斯分布时，多孔介质微观模型的迭代结果，以及迭代过程中孔隙度的变化.从迭代的结果可以看出，迭代的过程其实是固相颗粒的凝聚生长的过程，气相空间不断变小，孔隙度不断变小，在二维空间形成一些连通和不连通的空隙结构，固相颗粒大小和分布，这与常规的概念模型和统计模型更加接近真实的多孔介质.而且在不同的初始条件下这种方法可以演化出各种不同性质的多孔介质微观结构，均匀的或者各向异性，或者具有不同孔隙走向的多孔介质微观结构. 图3 初始固相 (μ=1, σ=0) Fig.3 initial solid phase (μ=1, σ=0) （b）迭代结果（a）高斯分布图2 初始固相(μ=1, σ=2) Fig.2 initial solid phase (μ=1, σ=2) （b）迭代结果（a）高斯分布（c）孔隙度随迭代变化（c）孔隙度随迭代变化0100 200 300 40050020406080100迭代次数/次 孔隙度/% 0100 200 300 400 50020406080100迭代次数/次 孔隙度/% 中国煤炭期刊网 www.chinacaj.net
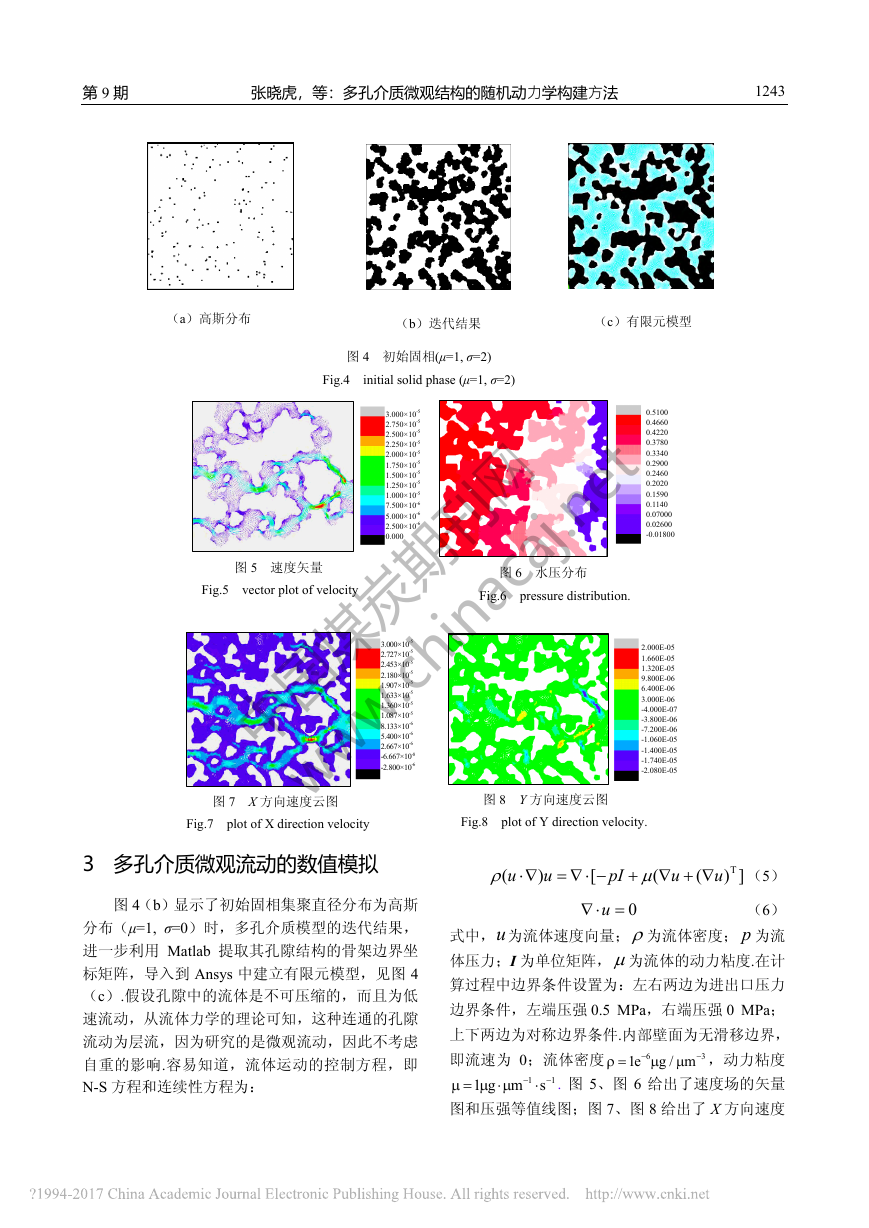
    第9期 张晓虎，等：多孔介质微观结构的随机动力学构建方法   1243 3 多孔介质微观流动的数值模拟 图4（b）显示了初始固相集聚直径分布为高斯分布（μ=1, σ=0）时，多孔介质模型的迭代结果，进一步利用Matlab提取其孔隙结构的骨架边界坐标矩阵，导入到Ansys中建立有限元模型，见图4（c）.假设孔隙中的流体是不可压缩的，而且为低速流动，从流体力学的理论可知，这种连通的孔隙流动为层流，因为研究的是微观流动，因此不考虑自重的影响.容易知道，流体运动的控制方程，即N-S方程和连续性方程为： T()[(()]uupIuu（5）0u （6） 式中，u为流体速度向量；为流体密度；p为流体压力；I为单位矩阵，为流体的动力粘度.在计算过程中边界条件设置为：左右两边为进出口压力边界条件，左端压强0.5 MPa，右端压强0 MPa；上下两边为对称边界条件.内部壁面为无滑移边界，即流速为0；流体密度631eg/m，动力粘度111gms. 图5、图6给出了速度场的矢量图和压强等值线图；图7、图8给出了X方向速度图4 初始固相(μ=1, σ=2) Fig.4 initial solid phase (μ=1, σ=2) （b）迭代结果 （a）高斯分布 图8 Y方向速度云图 Fig.8 plot of Y direction velocity. 图7 X方向速度云图 Fig.7 plot of X direction velocity（c）有限元模型 3.000×10-52.750×10-52.500×10-52.250×10-52.000×10-51.750×10-51.500×10-51.250×10-51.000×10-57.500×10-65.000×10-62.500×10-60.000 0.5100 0.4660 0.4220 0.3780 0.3340 0.2900 0.2460 0.2020 0.1590 0.1140 0.07000 0.02600 -0.01800 3.000×10-52.727×10-52.453×10-52.180×10-51.907×10-51.633×10-51.360×10-51.087×10-58.133×10-65.400×10-62.667×10-6-6.667×10-8-2.800×10-62.000E-05 1.660E-05 1.320E-05 9.800E-06 6.400E-06 3.000E-06 -4.000E-07 -3.800E-06 -7.200E-06 -1.060E-05 -1.400E-05 -1.740E-05 -2.080E-05 图6 水压分布 Fig.6pressure distribution. 图5 速度矢量 Fig.5 vector plot of velocity 中国煤炭期刊网 www.chinacaj.net
    辽宁工程技术大学学报（自然科学版） 第33卷  1244和Y方向速度云图.可以看出，速度场和压强场都存在很强的不规则性，流体运动路径曲折迂回，这与孔隙结构的分布是直接相关的，速度的极值都分布在较为狭窄的地方，X方向的速度极值出现在水平走向的孔隙中，而Y方向的速度极值则分布在45°走向的孔隙中.对这样的低速流动，其宏观渗透过程满足达西定律，通过出口流速对边界进行积分计算出流量，进而可以计算出所建微观模型的水平相对渗透率；另外可以利用第二节提出的模型建立多种不同孔隙度的多孔介质微观模型，来讨论孔隙率对多孔介质微观流动的影响；如果对多孔介质的固体骨架进行建模可以计算多孔介质微观结构的有效热导率，同时还可以研究多孔介质微观结构的热力耦合作用. 4 结 论 （1）基于朗之万程的多孔介质微观结构建模过程本身就是用自然的气相和固相相互作用过程， 临近的固相聚集生长，临近的孔隙相结合，生成的多孔介质微观结构与真实多孔介质非常接近. （2）模型具有明确的数学表达，同时物理意义很明确，易于实现. （3）通过不同的固相分布初始条件，本模型可以演化出各种不同性质的多孔介质微观模型，满足多孔介质微观建模方面的多种需求. 参考文献： [1] Scheidegger A E.the physics of flow through porous media[M].Third edition.University of Toronto Press,1977:4-9. [2] Civan Frank.Reservoir Formation Damage:Fundamentals,Modeling, Assessment And Mitigation[M].2ndEdition.Burlington:Gulf Professional Publishing,2007. [3] 李传亮,孔祥言,徐献之,等.多孔介质的双重有效应力[J].自然杂志,1999,21(5):288-291. Li Chuanliang,Kong Xiangyan,Xu Xianzhi.Double effective stresses of porous media[J].Ziran Zazhi,1999,2(15):288-291. [4] 邓彩华,童亮,陈壁峰,等.多孔介质流动的直接数值模拟[J].武汉理工大学学报,2011,35(6):1 257-1 260. Deng Caihua,Tong Liang,Chen Bifeng et al.Direct numerical simulation for fluid flow in porous media[J].Journal of Wuhan University of Technology,2011,35(6):1 257-1 260. [5] Perrier Edith, Bird Nigel, Rieu Michel. Generalizing the fractal model of soil structure: the pore-solid fractal approach[J].Geoderma,1999, 88(3-4):137-164. [6] Lehmann P,Stahli M,Papritz A.A fractal Approch to model soil structure and to calculate thermal conductivity of Soils[J].Transport in Porous Media,2003,52:313-332. [7] 张东辉,金峰,施明恒,等.多孔介质渗流随机模型[J].应用科学学报,2003,21(1):88-92. Zhang Donghui,Jin Feng,Shi Mingheng,et al.A random simulation method in porous media[J].Journal of Applied Science,2003,21 (1):88-92. [8] 张东辉,金峰,施明恒,等.分形多孔介质中的热传导[J].用科学学报, 2003,21(3):253-257. Zhang Donghui,Jin Feng,Shi Mingheng,et al.Heat conduction in fractal porous media[J].Journal of Applied Sciences,2003,21(3):253-257. [9] Wu Kejian,Van Dijke M.I.J.,G.D.Couples,et al.3D stochastic modelling of heterogeneous porous media-applications to reservoir rocks[J]. Transport in Porous Media,2006(65):443-467. [10] 袁锦越,杨彬彬,焦阳,等.多孔介质干燥过程分形孔道网络模型与模拟:II.数值模拟与试验验证[J].中国农业大学学报,2007,14(2):55-60. Yuan Yuejin,Yang Binbin, Jiao yang et al. Fractal pore network simulation on the drying of porous media:II.Experimental study and numerical simulation[J].Journal of China Agricultural University, 2007,14(2):55-60. [11] Okabe Hiroshi, Blunt Martin J.Prediction of permeability for porous media reconstructed usingmultiple-point statistics[J].Physical Review E, 2004,70:066135. [12] Al-Kharusi,Anwer S,Blunt Martin J.Multiphase flow predictions from carbonate pore space images using extracted network models[J].Water Resources Research,2008,44-1-14. [13] 鞠杨,杨永明,宋振铎,等.岩石孔隙结构的统计模型[J].中国科学E辑:技术科学,2008,38(7):1026-1041. Ju Yang, Yang Yongming, Song Zhenduo et al. Statistical model of pore structure in rock[J]. SCIENCE IN CHINA(SERIES E). 2008, 38(7):1026-1041 [14] Lin C L,Miller J D.Network analysis of filter cake pore structure by high resolution x-ray on industrialprocess tomography,uxton, greater microtomography[C].Resented at 1st World Congress Manchester,April 14-17,1999. [15] Vogel H J,Tolke J,Schulz V P.Comparison of a lattice-boltzmann model,a full- morphology model,and a pore network model for determining capillary pressure-saturation relationships[J].Vadose Zone Journal,2005(4):380-388. 中国煤炭期刊网 www.chinacaj.net
    第9期 张晓虎，等：多孔介质微观结构的随机动力学构建方法   1245[16] Okabe Hiroshi,Blunt Martin J.Pore space reconstruction of vuggy carbonates using microtomography and multiple-point statistics[J]. Water Resources Research,2007,43:W12s02. [17] Talabi Olumide,AlSayari Saif,Iglauer Stefan,et al.of Petroleum Science and Engineering,2009(67):168-178. [18] 张挺,卢德唐,李道伦.基于二维图像和多店统计方法的多孔介质三维重构研究[J].中国科学技术大学学报,2010,3(40):271-277. Zhang Ting,Lu Tangde,Li Daolun. A method of reconstruction of porous media using a two-dimensional image and multiple-point statistics[J].Journal of University of Science and Technology of China,2010,3(40):271-277. [19] 王波,宁正福,姬江,等.多孔介质模型的三维重构方法[J].西安石油大学学报,2012,4(27):54-61. Wang Bo,Ning Zhengfu,Ji Jiang. Study on 3D reconstruction methods of porous medium model[J].Journal of Xi’an Shiyou University: Natural Science Edition,2012,4(27):54-58. [20] Jacob Bear.dynamics of fluids in porous media[m].american elsevier publishing company,inc,1972,11-15. [21] 于明旭,朱维耀,宋洪庆.低渗透储层可视化微观渗流模型研制[J].辽宁工程技术大学学报:自然科学版,2013,32(12):1 646-1 650. Yu Mingxu,Zhu Weiyao,Song Hongqing.Development of microscopic visualization flow model of low-permeability reservoir[J].Journal of Liaoning Technical University:Natural Science,2013,32(12):1 646-1 650. [22] 黄海平,水庆象,徐兵.壁面驱动粘性不可压缩半圆形空腔流的数值模拟[J].辽宁工程技术大学学报:自然科学版,2013,32(10):1 393-1 398. Huang Haiping, Shui Qingxiang, Xu Bing.Numerical simulation of wall-driven incompressible viscous flow in a semi-circular cavity[J]. Journal of Liaoning Technical University:Natural Science,2013,32 (10):1 393-1 398. [23] 赵静,冯增朝,杨栋,等.CT实验条件下油页岩内部孔裂隙分布特征[J].辽宁工程技术大学学报:自然科学版,2013,32(8):1 044-1 049. Zhao Jing,Feng Zengchao,Yang Dong,et al.Study on distribution characteristics of pores and fissures inside oil shale under the CT experiment[J].Journal of Liaoning Technical University:Natural Science,2013,32(8):1 044-1 049. [24] 李林凯,姜瑞忠.低渗透油藏双重介质试井[J].辽宁工程技术大学学报:自然科学版,2013,32(3):353-356. Li Linkai,Jiang Ruizhong.Well test for low permeability double medium reservoirs[J].Journal of Liaoning Technical University: Natural Science,2013,32(3):353-356. [25] 李守巨,上官子昌,孙伟,等.多孔岩土材料渗透系数与孔隙率关系随机模拟[J].辽宁工程技术大学学报:自然科学版,2010,29(4):589-592. Li Shouju,Shangguan Zichang,Sun Wei,et al.Simulation on relationship between hydraulic conductivity and porosity for porous soils[J].Journal of Liaoning Technical University Natural Science, 2010,29(4).589-592. [26] 周建军,周辉,邵建富,等.饱和孔隙介质各向异性损伤细观模型[J].辽宁工程技术大学学报:自然科学版,2010,29(2):252-255. Zhou Jianjun,Zhou Hui,Shao Jianfu,et al.Micromechanical model of anisotropic damage for saturated porous media[J].Journal of Liaoning Technical University:Natural Science,2010,29(2):252-255. [27] 袁则循,毛灵涛,赵丹.基于数字地形模型土微结构三维孔隙度的计算方法[J].辽宁工程技术大学学报:自然科学版,2011,30(5):734-737. Yuan Zexun,Mao Lingtao,Zhao Dan.Computation method on 3D porosity of soil microstructure based on digital terrain model[J]. Journal of Liaoning Technical University:Natural Science,2011,30(5): 734-737. [28] Ken Elder.Langevin simulations of nonequilibrium phenomena[J]. Computers In Physics,1993,7(1):27-33. [29] 刘伟,范爱武,黄晓明.多孔介质传热传质理论与应用[M].北京:科学出版社,2006,5-6. Liu Wei, Fan Aiwu, Huang Xiaoming.Theory and application of heat and mass transfer in porous media[M].Science Press,2006,5-6 中国煤炭期刊网 www.chinacaj.net
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料