logo资料库

生物统计学与R极简手册.pdf

发布时间：2022-06-14 发布人：admin 分类：说明书 资料大小：1.20M 资料格式：pdf 举报 版权申诉
第1页 / 共35页
第2页 / 共35页
第3页 / 共35页
第4页 / 共35页
第5页 / 共35页
第6页 / 共35页
第7页 / 共35页
第8页 / 共35页
资料共35页，剩余部分请下载后查看
    生物统计学与R极简手册
    写在前面
    描述性统计量
    数据的集中趋势
    数据的变异性（离散性）
    计算描述性统计量
    形象化展示
    概率相关内容
    几个概念
    离散概率分布
    常见的离散概率分布
    连续概率分布
    估计
    相关性分析
    正态分布评估
    相关性分析
    相关性可视化展示
    Pearson 相关性检验
    单双样本均值分析
    假设检验一般步骤
    单样本t-test
    单样本Wilcoxon 符号秩检验
    独立双样本t-test
    独立双样本Wilcoxon test
    非独立双样本t-test
    非独立双样本Wilcoxon test
    多样本均值分析
    one-way ANOVA
    two-way ANOVA
    比例分析
    单比例检验
    双比例检验
    卡方分布
    常用高阶分析方法
    回归分析
    聚类分析
    k-means
    Hierarchical Clustering
    主成分分析
    生物统计学与R极简手册 作者：思考问题的熊 博客：http://kaopubear.top 写在前面 入门生物信息或者进行生物相关研究，所有人都绕不开统计的基础知识和计算实现方式。在担任中科院生物 统计学课程助教的过程中，我发现大部分同学的首要困惑在于理不清相关概念，其次才是不知道该如何用R语 言来进行最基本的计算。本合集共分为8小节，将简要介绍生物统计学相关基础知识以及如何使用R语言进行 最基本的计算和分析。 需要说明的是，文中个别描述严格来讲并不准确但希望有助于理解，涉及到R语言的部分则展示了若干函数最 基本用法，希望不给阅读和学习增加负担。另外，这份资料主要面向生物统计学和R语言基础薄弱的人群，勉 强可以称之为极简手册 ，详细的学习还需要阅读相关教材资料。 描述性统计量 为了解决某个问题，我们通常会观察一组和该问题相关的样本，利用总体中的部分样本来推断总体的情况进而得到 相关结论。在通过样本推断总体前，首先需用对已有样本数据进行简单的评估和描述，针对这一需求也就引出了描 述统计量这一概念。进行描述性统计时，我们最关注数据两个层面的问题：数据的集中趋势和变异分散性。 数据的集中趋势 面对少则几十多则上千个数字，第一步通常是观察平均水平。下面介绍三个计算数据平均水平的概念：分别是均值 (mean)、中位数(median)和众数(mode)。 均值：所有观察值的和除以观察的个数。算数平均是最自然和常用的测度，其问题在于对异常值(outliers)非常敏 感。有极端值存在时，均值不能代表样本的绝大多数情况。 中位数：所谓中位数，是指所有样本观测值由小到大排序，位于中间的一个（样本数为奇数）或者两个数据的平均 值（样本数为偶数）。 当数据分布对称时，中位数近似等于算数平均数；当数据正倾斜时（图像向右倾斜），中位数小于算数平均数；当 数据负倾斜时（图像向左倾斜），中位数大于算数平均数。因此，我们可以通过比较样本的均值和中位数对数据的 分布对称性进行初判断。 众数：在样本所有观测值中，出现频率最大（出现次数最多）的数值称为众数。这里需要说明，当数据量很大而且 数值不会多次重复出现时众数并不能带来太多信息。比如当计算上万个基因的表达量后，得到的众数最可能是0， 因为每个基因的表达值或多或少都有一些不同，这时候出现最多的就是那些没有检测到表达基因的0了。但是在遇 到类别数据而非数值型数据时众数有很大用处，或者说众数是唯一可以用于类别数据的平均数。 在R中，均值和中位数可以通过 mean() 和 median() 进行计算,而众数可以通过 modeest 包 mfv() 函数得到。 数据的变异性（离散性） 平均数显然不能说明一切问题，在说明样本数据时我们还必须考虑数据是不是过于分散。例如在篮球队员投篮平均 得分相同的情况下，更重要的是知道他们谁发挥更加稳定。
    极差(range)指一个样本中最大值和最小值之间的差值。在统计学中也称为全距，它能够指出数据的“宽度”（范 围）。但它和均值一样易受极端值影响，而且也会受样本量明显影响。 针对极差的缺点，统计学又引入分位数(quantiles)概念，通俗讲是把数据的“宽度”细分后再去进行比较从而更好地 描述数据的分布形态。分位数用三个点将从小到大排列好的数据分为四个相等部分，而这三个点也就是我们常说的 四分位数，分别叫做下四分位数，中位数和上四分位数。当然，除了四分位也可以计算十分位或者百分位。 分位数的引进能够说明数值的位置，但无法说明某数值在该位置出现的概率。为了说明数据的稳定程度，我们可以 考虑计算每个数据值到平均数的距离（此处可以脑补一个高瘦形的数据曲线和矮胖形的数据曲线），但样本中所有 观测值与均值偏差的和永远是0。为了解决这种正负距离相互抵消的问题，统计学又引入方差(variance)和标准差 (standard deviation)概念。 所谓方差指数值与均值距离平方数的平均数，而标准差则是方差的平方根。标准差体现了数据的变异度，标准差越 小，数值和均值越近。通常均值用 表示，而标准差用 表示。 在R中，可以通过 quantile() 计算分位数，通过 var() 来计算方差，通过 sd() 来计算标准差。 有了标准差的概念，随之而来的问题是当两个样本标准差相同但是均值相差很大时该如何做出区分。于是，统计学 引入了变异系数(coefficient of variation, CV) 概念，变异系数是指样本标准差除以均值再乘100%。变异系数不 会受数据尺度的影响，因此常用来进行不同样本之间变异性的比较。 在实际的数据分析中，如果要比较不同数据集(均值和标准差都不同)之间的数值，通常会引入z score的概念，z score 的计算方法是用某一数值减去均值在除以标准差。通过对原始数据进行z变换，我们将不同数据集转化为一个 新的均值为0，标准差为1的分布。 计算描述性统计量 在R中，使用 summary() 函数会得到一个data frame 的很多 描述性统计量。当数据某一列是数值型变量时，可以 得到该列数据的均值、极值、方差和分位数。 下面我们使用R中内置的数据Edgar Anderson's Iris Data进行一些简单展示。 summary(iris) #查看常用的描述统计量 Sepal.Length Sepal.Width Petal.Length Petal.Width Species Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50 Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50 Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 Max. :7.900 Max. :4.400 Max. :6.900 Max. 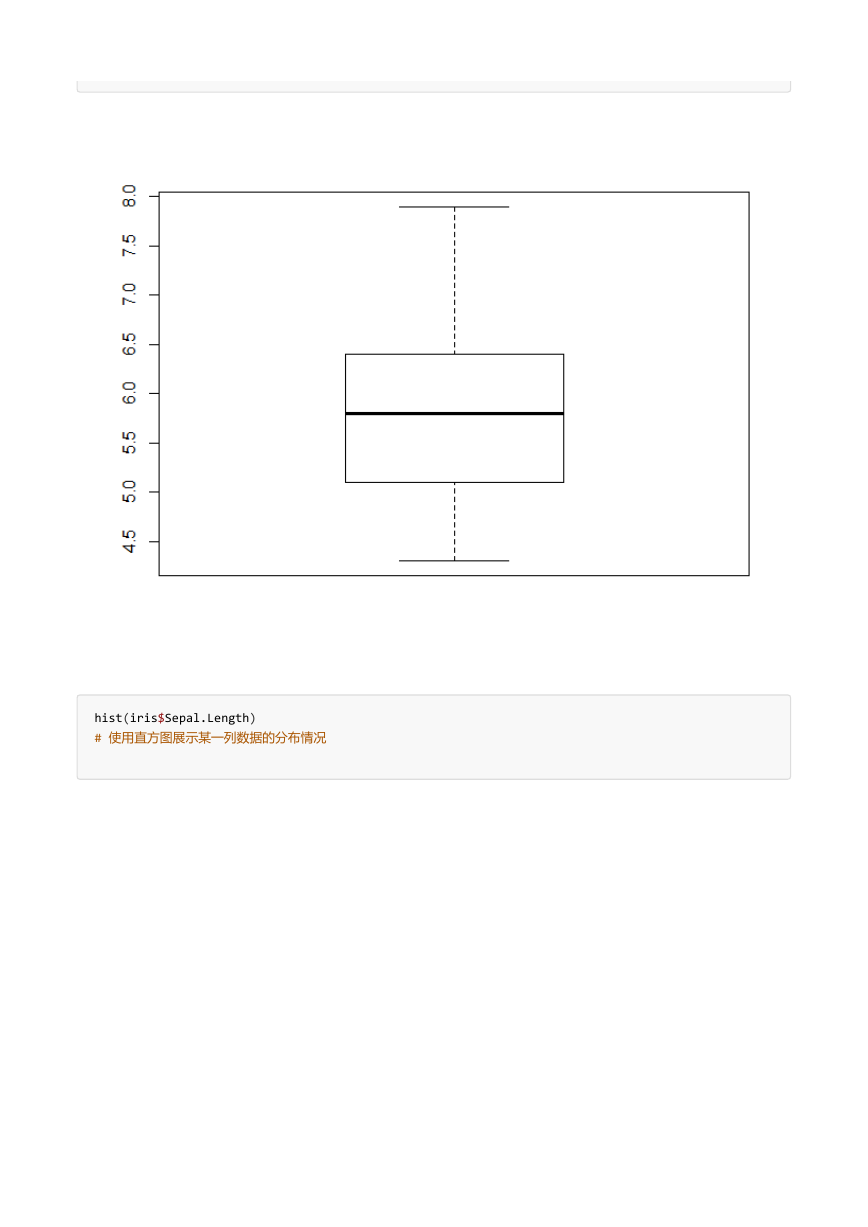:2.500 形象化展示 所谓形象化展示就是用图来展示数据结果，比较常见的方法有条形图，箱线图，直方图等 boxplot(iris$Sepal.Length) # 使用箱线图展示某一列数据的分布情况
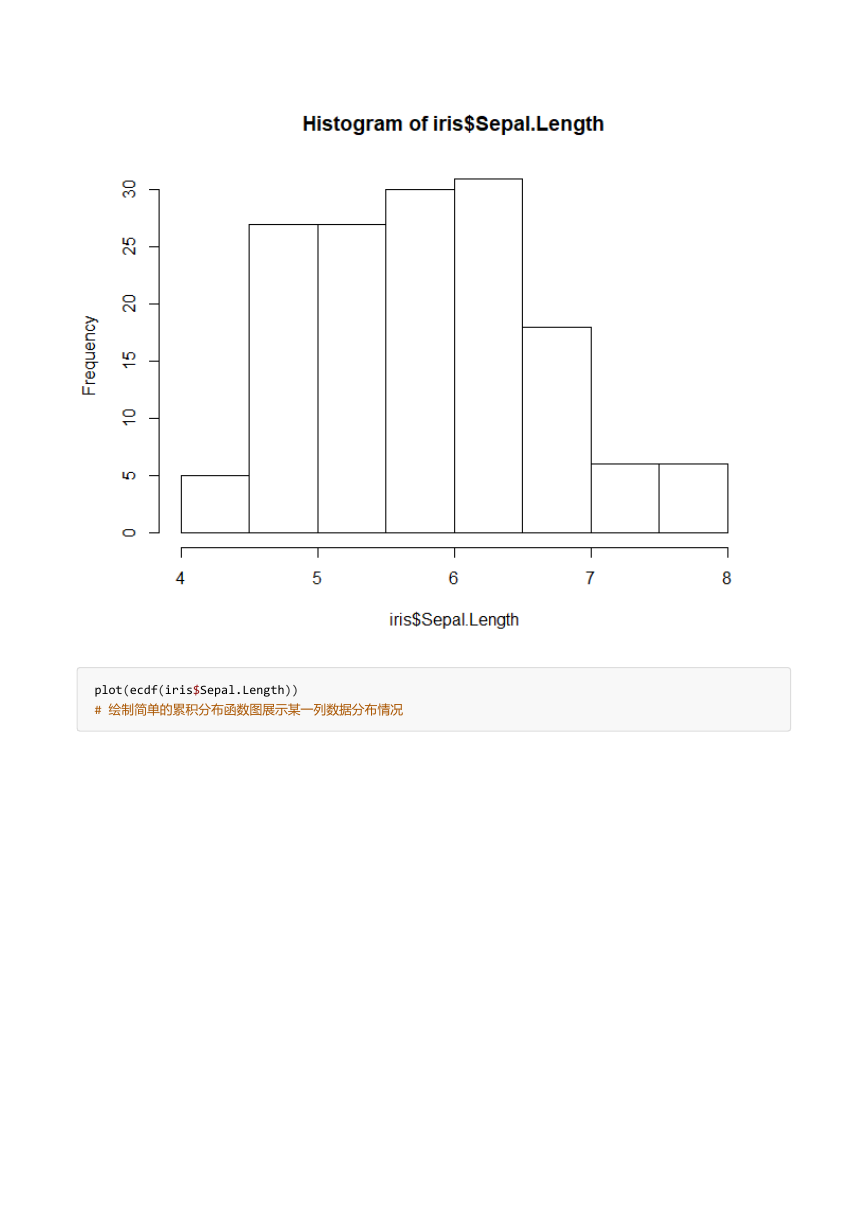
    hist(iris$Sepal.Length) # 使用直方图展示某一列数据的分布情况
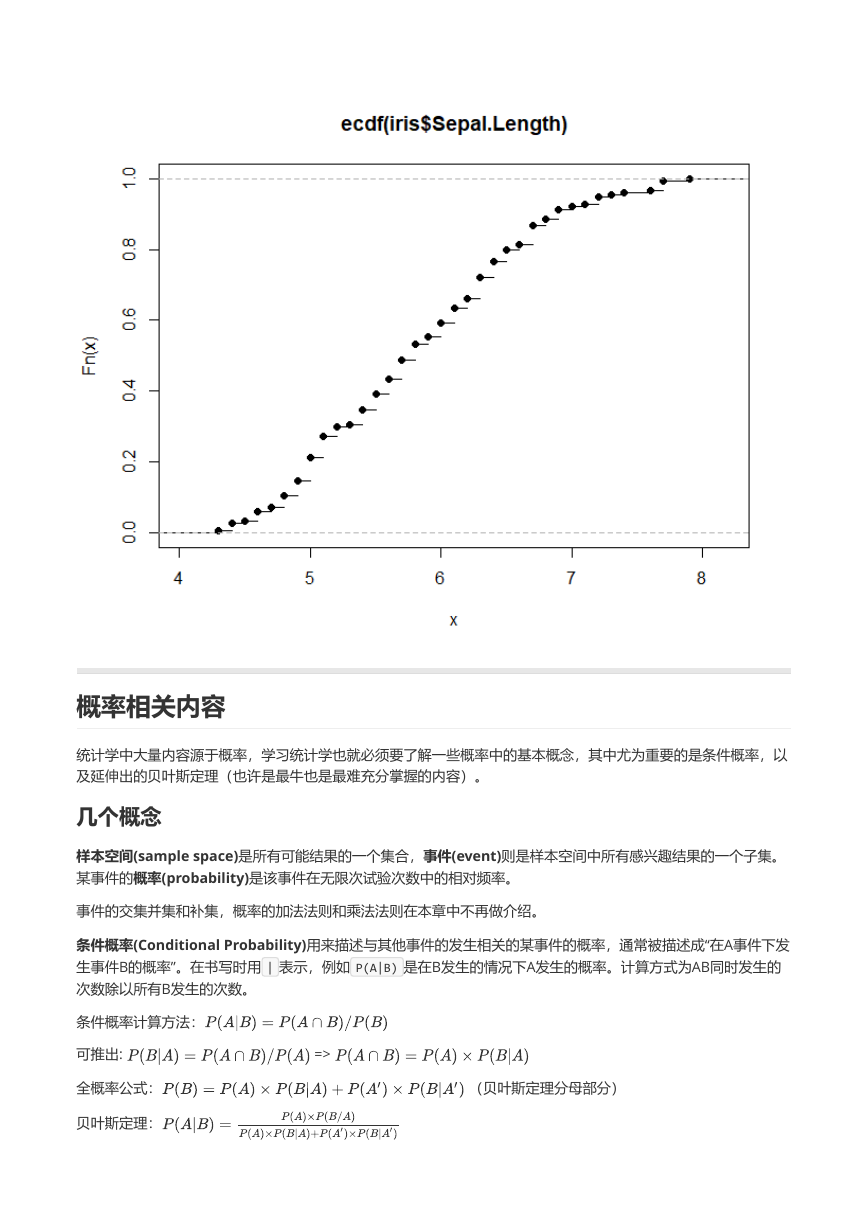
    plot(ecdf(iris$Sepal.Length)) # 绘制简单的累积分布函数图展示某一列数据分布情况
    概率相关内容 统计学中大量内容源于概率，学习统计学也就必须要了解一些概率中的基本概念，其中尤为重要的是条件概率，以 及延伸出的贝叶斯定理（也许是最牛也是最难充分掌握的内容）。 几个概念 样本空间(sample space)是所有可能结果的一个集合，事件(event)则是样本空间中所有感兴趣结果的一个子集。 某事件的概率(probability)是该事件在无限次试验次数中的相对频率。 事件的交集并集和补集，概率的加法法则和乘法法则在本章中不再做介绍。 条件概率(Conditional Probability)用来描述与其他事件的发生相关的某事件的概率，通常被描述成“在A事件下发 生事件B的概率”。在书写时用 | 表示，例如 P(A|B) 是在B发生的情况下A发生的概率。计算方式为AB同时发生的 次数除以所有B发生的次数。 条件概率计算方法： 可推出: 全概率公式： 贝叶斯定理： => （贝叶斯定理分母部分）
    得到的贝叶斯定理可以帮助我们计算逆条件概率。 在实际的生物学数据处理的过程中，我们还会接触到灵敏度(sensitivity)、特异度(specificity)、假阳性(false negative)和假阴性(false positive) 几个概念。在疾病相关研究中，对于某一个症状，灵敏度指发病后出现症状的 概率，特异度是不发病时不出现症状的概率。假阳性是指实验结果阳性但是实际为阴性，假阴性是指实验结果为阴 性但是实际为阳性。基于灵敏度和特异度可以使用ROC曲线，通常来说在两个检验中，曲线下面积大的较好。 概率能够告诉我们事件发生的可能性，但如果想要利用概率预测未来的结果并且评估预测的确定性就需要引入概率 分布。 离散概率分布 随机变量： 样本空间中，对不同事件指定有相应概率的数值函数。 ，表示随机变量X 随机变量是可以等于一系列数值的变量，这些值都和一个特定概率关联。它的写法是 取特定值为x时的概率。随机变量包括离散和连续两种形式，所谓离散指变量只能取一些确定值。连续指的是有无 限多种可能取值。 概率分布也叫概率质量分布， 。在描述统计量中，样本的频数分布描述每个取值及对应发生次数，如果 样本总数除以对应发生次数，得到的频率分布就类似于这里的概率分布。后面会提到的“拟合优度检验”就是比较有 限样本频率分布和概率分布的差异。 如果将随机变量和样本对应起来理解，样本中均值的概念在总体（随机变量）中称为期望，也叫作总体均值，表示 为 （和均值一致）或者 。计算方式是将每个可能值和概率相乘再把所有乘积相加。和均值类似，这里的期 望也无法描述相关数值分散程度。 同样，在随机变量中也有类似于样本方差的概念，称为总体方差（随机变量方差），用来表示分散程度。其计算公 式为 。而概率分布的标准差 同样是方差的平方根。 计算 时，首先计算每个数值x的 ,然后再将结果乘以概率，最后把所有结果相加。 在数据集中，方差和标准差表示的是数据和均值的距离，在概率分布中表示特定数值概率的分散情况。方差越小， 结果越接近期望。 累加分布函数(cumulative-distribution function, cdf): 随机变量X，对于X的任一指定值x，概率值 即随机变量取值不大于指定值的概率。记作 常见的离散概率分布 。 几何分布：进行一组相互独立实验，每次实验有成功失败两种可能且每次试验概率相等，想知道第一次成功需要进 行的试验次数。 期望 ；方差 二项分布：进行一组相互独立试验，每次实验有成功失败两种可能，每次试验概率相等且 有限次试验中成功的次数。 ；方差 期望 ，想知道在 二项分布和几何分布差别在于，前者试验次数固定求成功概率，后者求第一次成功前试验次数。 泊松分布：常与稀有事件相关，单独事件在给定区间（区间可以是时间或者空间）内随机独立发生，该区间内的事 件平均发生次数已知且为有限值。这个值用 表示。给定区间内发生r次事件的概率计算公式： 期望是给定区间内能够期望的事件发生次数λ，方差也是λ。如果一个离散随机变量的一批数据计算后方差和均值近 似相等，则可以推测样本符合泊松分布。 试 验 次 数 有 限
    当二项分布的p很小且n非常大时， 简化。通常，n大于50且p<0.1时为典型的近似情况。 连续概率分布 ,方差和期望近似相等，可以用泊松分布来近似二项分布，从而使计算 当数据连续分布，人们关心的是取得某一个特定范围的概率。 概率密度函数(probability density function, pdf):本质是一个函数，用这个函数可以求出在一个范围内某连续变 量的概率，同时该函数可以指出该概率分布的形状。换句话讲，任意a,b两点之间及函数对应曲线下组成的面积等 于随机变量X落在ab间的概率。曲线下面积总和是1。 概率密度可以指出各种范围内的概率大小，用面积来表示。概率密度只是表示概率的一种方法而非概率本身。 累加分布函数a点上的值等于随机变量X取值 的概率，也是概率密度函数a左边曲线下的面积。 正态分布是连续数据的一种理想状态。正态分布的概率密度函数是一条对称的钟形曲线，均值具有最大的概率密 度，偏离均值概率密度逐渐变小。参数 是均值，也是曲线的中央位置， 表述曲线的“胖瘦”。 连续随机变量X符合均值为 ，标准差为 的正态分布时写作 . 线性变换： 当X和Y相互独立（彼此之间没有影响）时： ；方差 望 期 当X和Y并不彼此独立时，使用协方差(Covariance)来描述两个随机变量间的关系，记做Cov(X,Y) 二项分布正态近似：通常情况，当二项分布满足 中 , 。另外，当泊松分布的λ>15时，也可以用正态分布进行近似。 (也有建议 )时，可以用正态分布代替二项分布。其 估计 在通常的试验中我们获得的信息总是来自样本，想要知道总体的参数，只能通过已有样本参数进行估计。 样本均值是总体均值的点估计，通常样本均值用 表示，总体均值用 表示。 在估计总体方差 时，计算公式为 用样本方差估计总体方差会使得估计结果偏低，样本越小两个方差的差别可能就越大。在这里，估计总体方差的公 式中除的是 ，能够更接近总体方差。另外，总体方差点估计公式通常记做 ,写作： 用样本均值估计总体均值时也会产生误差，均值的标准误差是 。标准误差表示了样本均值 的分散情况，从公式中我们可以看出，n越大，用样本均值估计总体均值越准确。当样本足够大（大于30），即便 总体不符合正态分布，但从中取出的样本均值分布仍然近似于正态分布（中心极限定理）。 ，估计量是 除了对总体进行点估计以外，我们往往还会对总体进行区间估计，即对通过点估计得到的结果加减一定范围的误 差。 相关性分析
    本节提到的相关性分析和后面会提到的t-test, ANOVA 以及回归分析等被称为参数检验，这些检验在进行时我们常 默认数据符合一定前提条件，如符合正态分布和方差相等等。当样本数量大于30时，根据中心极限定理，我们通常 认为数据符合正态分布；在进行t-test 和ANOVA 分析时，还需要满足样本方差相等。 在进行各种检验之前需要初步检验数据是否符合某种检验的前提条件，如果不符合则应该考虑使用非参数检验或其 他方法。 正态分布评估 在评估数据集是否符合正态分布时通常会采用Shapiro-Wilk’s test和图示(Q-Q plot)结合的方法。使用Q-Q plot(quantile-quantile plot)的结果较直观，使用Shapiro-Wilk’s test显著性检验的方法更准确（相对而言）。 Shapiro-Wilk’s test 结果受样本量的影响非常大，当样本量很大时即便数据符合正态分布也容易出现p值很小进而 拒绝原假设的情况（该检验原假设是样本来自于正态分布）。样本量很小时即便真实数据不s是来自正态分布，也 可能接受原假设。 这里试举一例 # 分别随机生成两组二项分布和指数分布随机数 set.seed(90) x <- rbinom(15,8,0.7) y <- rexp(15,0.5) shapiro.test(x) shapiro.test(y) # Shapiro-Wilk normality test # # data: x # W = 0.95996, p-value = 0.6917 # # # Shapiro-Wilk normality test # # data: y # W = 0.96168, p-value = 0.7216 可以发现，即便我们生成的两个样本都不是正态分布，但是检验的结果仍然没有拒绝原假设（没有拒绝不等于接受 原假设）。好在R中该函数限制检测的样本个数是3到5000。因此，同时结合图像来分析还是很必要的。 一般使用Q-Q plot来检验是否符合正态分布，R中默认的函数是 qqnorm() ；ggplot2中可以使用函数 qplot() ； qqpubr包是基于ggplot2二次开发的简易升级版，操作更加友好，可以使用函数 ggqqplot() 。 下面利用生成的数据绘图。
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料