第1页 / 共32页
第2页 / 共32页
第3页 / 共32页
第4页 / 共32页
第5页 / 共32页
第6页 / 共32页
第7页 / 共32页
第8页 / 共32页
电力系统潮流计算(高斯-赛德尔法)实验报告.doc
电力系统分析实验报告
学生姓名：
学
号：
专业班级：
实验类型：□ 验证 □ 综合 ■ 设计 □ 创新 实验日期：
实验成绩：
一、实验项目名称
二、实验目的与要求：
P-Q 分解法潮流计算实验
目的：电力系统分析的潮流计算是电力系统分析的一个重要的部分。通过对电力系
统潮流分布的分析和计算，可进一步对系统运行的安全性，经济性进行分析、评估，提
出改进措施。电力系统潮流的计算和分析是电力系统运行和规划工作的基础。
潮流计算是指对电力系统正常运行状况的分析和计算。通常需要已知系统参数和条
件，给定一些初始条件，从而计算出系统运行的电压和功率等；潮流计算方法很多：高
斯-塞德尔法、牛顿-拉夫逊法、P-Q 分解法、直流潮流法，以及由高斯-塞德尔法、牛顿
-拉夫逊法演变的各种潮流计算方法。
本实验采用 P-Q 分解法进行电力系统分析的潮流计算程序的编制与调试，获得电力
系统中各节点电压，为进一步进行电力系统分析作准备。通过实验教学加深学生对电力
系统潮流计算原理的理解和计算，初步学会运用计算机知识解决电力系统的问题，掌握
潮流计算的过程及其特点。熟悉各种常用应用软件，熟悉硬件设备的使用方法，加强编
制调试计算机程序的能力，提高工程计算的能力，学习如何将理论知识和实际工程问题
结合起来。
要求：编制调试电力系统潮流计算的计算机程序。程序要求根据已知的电力网的数学模
型（节点导纳矩阵）及各节点参数，完成该电力系统的潮流计算，要求计算出节点电压、
功率等参数。
三、主要仪器设备及耗材
每组计算机 1 台、相关计算软件 1 套
四、实验内容：
1.理论分析：
P-Q 分解法是从改进和简化牛顿法潮流程序的基础上提出来的，它的基本思想是：
把节点功率表示为电压向量的极坐标方程式，抓住主要矛盾，以有功功率误差作为修
正电压向量角度的依据，以无功功率误差作为修正电压幅值的依据，把有功功率和无
功功率迭代分开来进行。
牛顿法潮流程序的核心是求解修正方程式，当节点功率方程式采取极坐标系统时，
修正方程式为：
或展开为：
P
Q
H
J
N
L
VV
/
HP
JQ
/
VVN
VVL
/
(4)
以上方程式是从数学上推倒出来的，并没有考虑电力系统这个具体对象的特点。
电力系统中有功功率主要与各节点电压向量的角度有关，无功功率则主要受各节点
电压幅值的影响。大量运算经验也告诉我们，矩阵 N 及 J 中各元素的数值相对是很小
的，因此对牛顿法的第一步简化就是把有功功率和无功功率分开来进行迭代，即将式(4)
化简为：
HP
/
VVLQ
(5)
这样，由于我们把 2n 阶的线性方程组变成了二个 n 阶的线性方程组，因而计算量
和内存方面都有改善。但是，H ，L 在迭代过程中仍然不断变化，而且又都是不对称
矩阵。对牛顿法的第二个化简，也是比较关键的一个化简，即把式(5)中的系数矩阵简
化为在迭代过程中不变的对称矩阵。
众所周知，一般线路两端电压的相角差是不大的(通常不超过 10~20 度)，因此可以
认为：
cos
G
ij
ij
sin
1
ij
B
ij
此外，与系统各节点无功功率相应的导纳 LiB 必定远远小于该节点自导纳的虚部，
(6)
即：
B
Li
Q
i
2
V
i
B
ii
因此，
Q
i
2
V B
ii
i
(7)
考虑到以上关系后，式(5)中系数矩阵中的元素表达式可以化简为：
ij
ii
2
H V B
ii
H VV B
ij
L
ii
L
ij
i
j
2
V B
i
ii
VV B
i
ij
i
j
这样，式(5)中系数矩阵可以表示为：
(8)
21
n
n
H L
n
VV B
1
1
n
V V B
2
2
2
V B
n
nn
2
V B
1
11
V V B
2 1
V V B
1
1
n
n
VV B
12
1 2
2
V B
2
22
V V B
n
n
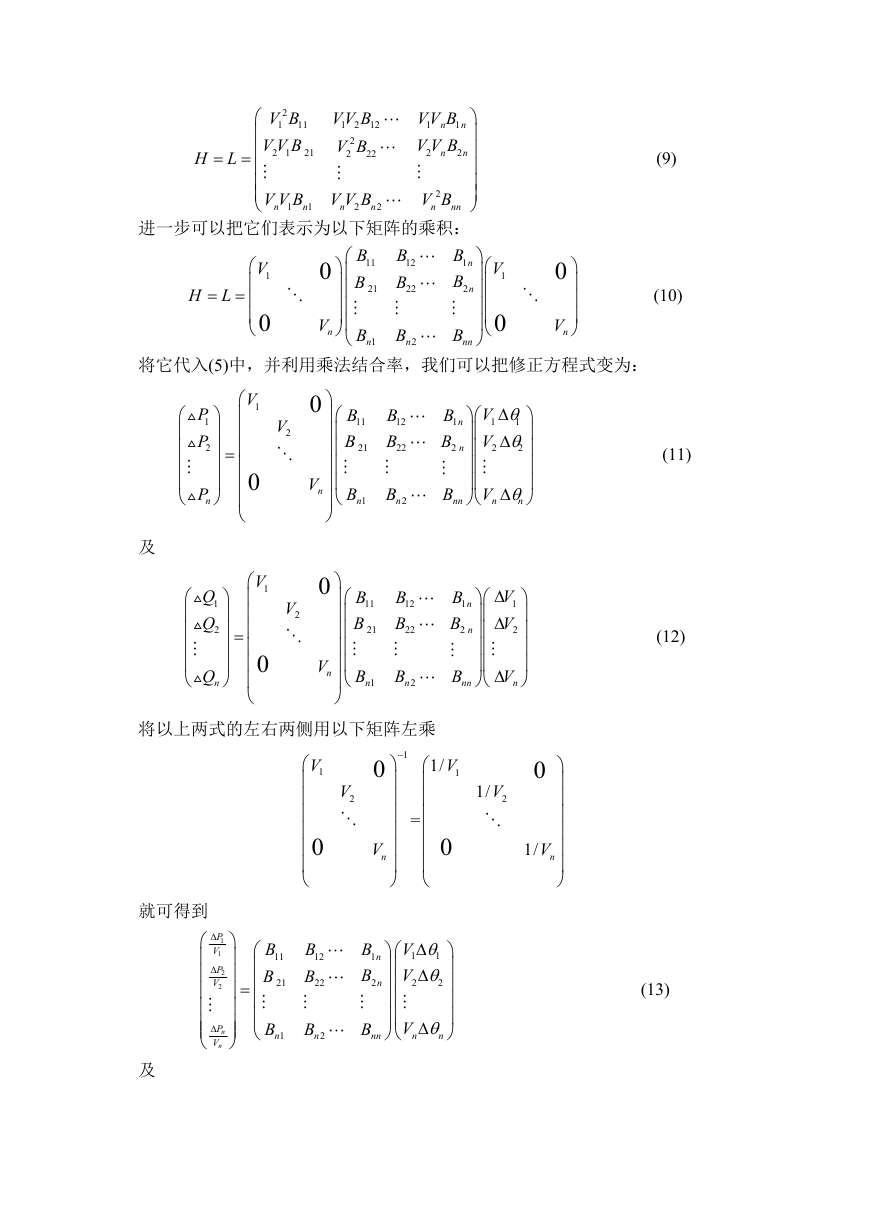
进一步可以把它们表示为以下矩阵的乘积：
B
1
B
2
B
nn
B
11
B
B
1
n
B
12
B
22
B
n
2
H L
V
1
0
2
2
0
V
n
21
n
n
V
1
0
0
V
n
(9)
(10)
(11)
(12)
将它代入(5)中，并利用乘法结合率，我们可以把修正方程式变为：
P
1
P
2
P
n
V
1
0
V
2
0
V
n
21
B
11
B
B
1
n
B
12
B
22
B
n
2
及
Q
1
Q
2
Q
n
V
1
0
V
2
0
V
n
21
B
11
B
B
1
n
B
12
B
22
B
n
2
将以上两式的左右两侧用以下矩阵左乘
n
n
B
1
B
2
B
nn
V
1
V
2
V
n
1
2
n
n
n
B
1
B
2
B
nn
V
1
V
2
V
n
V
2
V
1
0
1/
V
1
0
1
0
V
n
=
1/
V
2
0
1/
V
n
就可得到
P
1
V
1
P
2
V
2
P
n
V
n
及
21
B
11
B
B
1
n
B
12
B
22
B
n
2
n
n
B
1
B
2
B
nn
V
1
V
2
V
n
1
2
n
(13)
Q
1
V
1
Q
2
V
2
Q
n
V
n
21
B
11
B
B
1
n
B
12
B
22
B
n
2
n
n
B
1
B
2
B
nn
V
1
V
2
V
n
(14)
以上两式就是 P-Q 分解法达到修正方程式，其中系数矩阵只不过是系统导纳矩阵的
虚部，因而是对称矩阵，而且在迭代过程中维持不变。它们与功率误差方程式
GV
ij
j
cos
ij
B
ij
sin
ij
VPP
i
i
is
i
3,2,1(
nj
j
)
n
1
VQQ
i
is
i
nj
j
1
GV
ij
j
sin
ij
B
ij
cos
ij
（15）
（16）
(
i
3,2,1
n
)
构成了 P-Q 分解法迭代过程中基本计算公式，其迭代步骤大致是：
(1)根据求得的 Y 矩阵形成有功迭代和无功迭代的简化雅可比矩阵
`, BB
``
。
(2)给定各节点电压相角初值和各节点电压初值 (0)
iV
i
,
(0)
;
(2)根据(15)计算各节点有功功率误差 iP ，并求出 /
iP V
i
;
(3)解修正方程式(13)，并进而计算各节点电压向量角度的修正量 i
(4)修正各节点电压向量角度 i ；
)
k
(
i
(
i
k
)1
(
i
k
)1
(17)
(5)根据式(16)计算各节点无功功率误差 iQ ，计算时电压相角用最新的修正值，并求出
iQ V
i
/
;
(6)解修正方程式(14)，求出各节点电压幅值的修正量 iV
(7)修正各节点电压幅值 iV
(
k
)
V
i
V
i
(
k
)1
V
i
(
k
)1
(18)
(8)返回(2)进行迭代，直到各节点功率误差及电压误差都满足收敛条件。
2.理论数据：
j
z
13
1.1
j
,3.0
k
j
j
j
,
40.0
,50.0
,40.0
10.0
12.0
08.0
,
.0
01528
y
y
210
120
410
01920
.0
140
y
j
y
.0
01413
y
y
j
在上图所示的简单电力系统中，网络各元件参数的标么值如下：
z
12
z
14
z
24
系统中节点 1、2 为 PQ 节点，节点 3 为 PV 节点，节点 4 为平衡节点，已给定
P1s+jQ1s=-0.30-j0.18 P2s+jQ2s=-0.55-j0.13 P3s=0.5 V3s=1.10 V4s=1.05∠0°
容许误差ε=10-5
节点导纳矩阵：
240
420
各节点电压：
节点
1.
2.
3.
4.
各节点功率：
e
f
v
0.984637 -0.008596
0.958690 -0.108387
0.128955
1.092415
1.050000
0.000000
0.984675
0.964798
1.100000
1.050000
ζ
-0.500172
-6.450306
6.732347
0.000000
节点
1
P
Q
-0.300000 -0.180000
–0.550000
0.500000
0.367883
输入数据
-0.130000
-0.551305
0.264698
2
3
4
5
3.实验程序：
n=input('please enter the short value n:');
k=zeros(n,n);z=zeros(n,n);Y=zeros(n,n);yd=zeros(n,n);y=zeros(n,n);
% 其中 yd(i,j)表明 i,j 结点间与 i 结点接地电阻，y(i,j)表明 i,j 结点间正常联接电阻。
%
z(1,2)=0.10+0.4*i;z(1,3)=0.3*i;
z(1,4)=0.12+0.5*i;z(2,4)=0.08+0.4i;
yd(1,2)=0.01528*i;yd(2,1)=0.01528*i;yd(1,4)=0.01920*i;yd(4,1)=0.01920*i;
yd(2,4)=0.01413*i;yd(4,2)=0.01413*i;
k(1,3)=1.1;
% 数据处理%
for m=1:n
for j=1:n
if z(m,j)~=0
y(m,j)=1/z(m,j);
y(j,m)=y(m,j);
end
end
end
for m=1:n
for j=1:n
if k(m,j)~=0
y(m,j)=k(m,j)/z(m,j);
y(j,m)=y(m,j);
yd(m,j)=(k(m,j)-1)*k(m,j)/z(m,j);
yd(j,m)=(1-k(m,j))/z(m,j);
end
end
end
for m=1:n
for j=1:n
if m==j
Y(m,j)=sum(y(m,:))+sum(yd(m,:));
Y(m,j)=-y(m,j);
Y(j,m)=Y(m,j);
else
end
end
end
Y
A=[-0.3,-0.55,0.5,0;-0.18,-0.13,0,0;1,1,1.1,1.05;0,0,0,0];
G=real(Y);
B=imag(Y);
B1=B([1,2,3],[1,2,3]);
B2=B([1,2,],[1,2,]);
for k1=0:100
for m=1:(n-1)
sum=0;
for j=1:n
h=A(3,m)*A(3,j)*(G(m,j)*cos(2*pi/360*(A(4,m)-A(4,j)))+B(m,j)*sin(2*pi/360*(A(4,m)-A(4,
j))));
sum=sum+h;
end
op(1,m)=A(1,m)-sum;
end
V1=A([3],[1,2,3]);
a=op./V1; a=a*inv(-B1)*180/pi;
os=V1.\a;
A([4],[1,2,3])=A([4],[1,2,3])+os;
for m=1:2
sum=0;
for j=1:n
w=A(3,m)*A(3,j)*(G(m,j)*sin(2*pi/360*(A(4,m)-A(4,j)))-B(m,j)*cos(2*pi/360*(A(4,m)-A(4,
j))));
sum=sum+w;
end
oq(1,m)=A(2,m)-sum;
end
V2=A([3],[1,2]);
b=oq./V2;b=b*inv(-B2);
V2=V2+b;
A([3],[1,2])=A([3],[1,2])+b;
if max(max(abs(op)),max(abs(oq)))<0.00001
break;
end
end
sum=0; sum1=0;
for j=1:n
sum2=0;
x=A(3,4)*A(3,j)*(G(4,j)*cos(2*pi/360*(A(4,4)-A(4,j)))+B(4,j)*sin(2*pi/360*(A(4,4)-A(4,j)))
);
sum=sum+x;
c=A(3,4)*A(3,j)*(G(4,j)*sin(2*pi/360*(A(4,4)-A(4,j)))-B(4,j)*cos(2*pi/360*(A(4,4)-A(4,j))))
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
