中科大算法设计与分析.doc-资料库

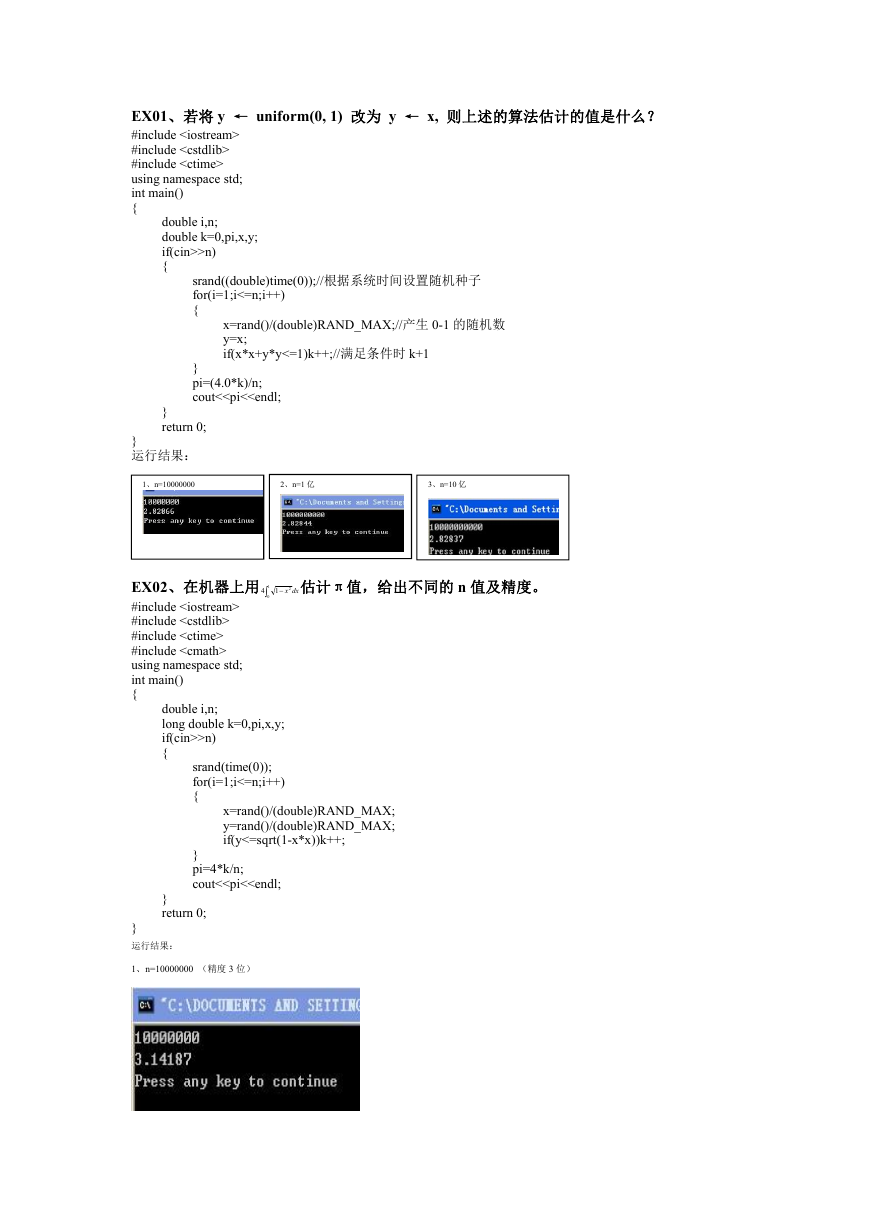
u010066564-6797115-4744302543436677732.doc.pdf-第1页.png

第1页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第2页.png

第2页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第3页.png

第3页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第4页.png

第4页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第5页.png

第5页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第6页.png

第6页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第7页.png

第7页 / 共10页

u010066564-6797115-4744302543436677732.doc.pdf-第8页.png

第8页 / 共10页

EX01、若将 y ← uniform(0, 1) 改为 y ← x, 则上述的算法估计的值是什么？ #include #include #include using namespace std; int main() { srand((double)time(0));//根据系统时间设置随机种子 for(i=1;i<=n;i++) { x=rand()/(double)RAND_MAX;//产生 0-1 的随机数 y=x; if(x*x+y*y<=1)k++;//满足条件时 k+1 double i,n; double k=0,pi,x,y; if(cin>>n) { } pi=(4.0*k)/n; cout< #include #include #include using namespace std; int main() { double i,n; long double k=0,pi,x,y; if(cin>>n) { srand(time(0)); for(i=1;i<=n;i++) { } return 0; } 运行结果： 1、n=10000000 （精度 3 位） x=rand()/(double)RAND_MAX; y=rand()/(double)RAND_MAX; if(y<=sqrt(1-x*x))k++; } pi=4*k/n; cout<

2、n=1 亿（精度 4 位） 3、n=10 亿 EX03、设 a, b, c 和 d 是实数，且 a <=b, c<=d, f:[a, b] → [c, d]是一个连续函数，写一概率算法计算积分： dxxfb )(  a 取被积函数为 f(x)=x*x-2*x+1 #include #include #include using namespace std; double (*pt_func)(double,double); double pfun(double i,double j) { return (j-i*i+2*i); } int main() { double n; double x,y; pt_func=pfun; if(cin>>n) { } return 0; } 1、n=10000000 2、n=1 亿 double f,k=0; srand(time(0)); for(int i=1;i<=n;i++) { x=rand()/(double)RAND_MAX; y=rand()/(double)RAND_MAX; if((*pt_func)(x,y)<=1) k++; //cout<<(*pt_func)(x,y)<

3、n=10 亿 EX04、分析 dlogRH 的工作原理，指出该算法相应的 u 和 v。 log g,p (s t mod p)=(log g,p s+log g,p t )mod (p-1) log g,p (g r mod p)=r 1 2 dlogRH(g, a p) { // 求 logg,p a, a = gx mod p，求 x for 0≤r≤p-2 // Sherwood 算法 ①r ← uniform(0..p-2); ②b ← ModularExponent(g, r, p); //求幂模 b=grmod p ③c ← ba mod p; //((g r modp)(g x modp)) mod p=gr+x mod p=c ④y ← logg,pc; // 使用确定性算法求 logp,gc, y=r+x ⑤return (y-r) mod (p-1); // 求 x } 解：（1）工作原理 ①r ← uniform(0..p-2); ②b ← ModularExponent(g, r, p); 这两步是随机过程，r 是随机的，所以 b 也是随机的，其中 b=g r mod p。 ③c ← ba mod p 其中 a = g x mod p，x 是函数待返回的值，代入 a，b 得 c =ba mod p =（g r mod p）*（g x mod p）mod p ④y ← log g,pc;代人 c 得 y=log g,pc =log g,p ((g r mod p)*(g x mod p)mod p) 由定理①得 y=[log g,p (g r mod p)+ log g,p(g x mod p)]mod (p-1) 再由定理②得 log g,p (g r mod p)=r ， log g,p (g x mod p)=x 可得 y=(r+x) mod (p-1) ，定理 P877,31.6 for 由上式可知 x=(y-r)mod (p-1) 此即语句⑤的返回值。 0≤r≤p-2, 0≤x≤p-2 （2）此算法中 u，v u(a,r)=(g r mod p)*(g a mod p)mod p //a 是输入实例，r 随机产生，转化为随机实例 v(r,y)=(y-r)mod (p-1) //y 是随机实例的解 EX05、用 SetCount (X)算法，估计整数子集 1~n 的大小，并分析 n 对估计值的影响。 SetCount (X) { k ← 0; S ← Ф; a ← uniform(X); do { k++; S ← S∪{a}; a ← uniform(X); } while (a ∉ S) return 2k 2/π； } 代码： #include #include #include #include #define pi 3.14159265 #define N 5000 using namespace std; int arr[N],k=0; bool inArr(int b) { for(int i=0;i<=k;i++) return false; if(b==arr[i]) return true; } double setcount(int x) {

int a; srand(time(0)); a=((x-1)*rand()/RAND_MAX)+1; cout<>n) return 0; } 运行结果： cout< #include #include #include int n=7,head=4; int val[7]={2,3,13,1,5,21,8}; int ptr[7]={1,4,5,0,6,-1,2}; int search(int x,int i) { } cout<<"共查找了"<val[i]) { i=ptr[i]; k++; } int A(int x) { } int B(int x) { return search(x,head); int y,i=head; int max=val[i]; for(int j=i;j

y=val[j]; if(maxy) return search(x,head); return search(x,ptr[i]); cout<>value; cout<<"A 算法搜索:";A(value); cout<<"B 算法搜索:";B(value); cout<<"C 算法搜索:";C(value); cout<<"D 算法搜索:";D(value); } 运行结果： EX07、证明：当放置（k+1)th 皇后时，若有多个位置是开放的,则算法 QueensLV 选中其中任一位置的概率相等。证明：用 P(k)表示选择第 k 个可用位置的概率（1≤k≤nb）。循环第一次找到可用位置时（i=2），nb←1,此时的肯定有 uniform(1..nb)=1，此时 p（1）=1；循环第二次找到可用位置时（i=4），nb←2,此时 uniform(1..nb)=1 的概率为 1/2，则 p（1）=1/2,p(2)=1/2; 循环第三次找到可用位置时（i=5），nb←3,此时 uniform(1..nb)=1 的概率为 1/3 则 p（3）=1/3; 而选第 2 个可用位置的概率 p（2）=1/2×（1－p(3)）=1/3，即第 2 次选第 2 个可用位置，且第 3 次不选第 3 个可用位置。而选择第 1 个可用位置的概率 p(1)=1×(1－1/2)×（1－1/3）=1/3，即第 1 次选第 1 个可用位置，并且第 2 次不选第 2 个可用位置，第 3 次也不选第 3 个可用位置。类似的证明一般情况：

假设循环找到最后一个可用位置时 nb=k（k≥2，即共有 k 个可用位置），则选择第 k 个可用位置的概率显然是 p(k)=1/k，下面计算 p（k－1），若要选择第 k－1 个可用位置必须满足两个条件; ①nb=k－1 时，uniform(1..nb)=1，第 k-1 次选第 k-1 个可用位置位置。 ②nb=k 时 uniform(1..nb)≠1，第 k 次不选第 k 个可用位置则 P(k-1)=(1/(k-1))(1-p(k))=(1/(k-1))(1-1/k)=1/k; 计算 p（k－2），若要选择第 k－2 个可用位置必须满足三个条件： ①nb=k－2 时，uniform(1..nb)=1，第 k-2 次选第 k-2 个可用位置 ②nb=k－1 时，uniform(1..nb)≠1，第 k-1 次不选第 k-1 个可用位置 ③nb=k 时，uniform(1..nb)≠1，第 k 次不选第 k 个可用位置 P(k-2)=(1/(k-2))(1-p(k-1))(1-p(k))=(1/(k-2))(1-1/(k-1))(1-1/k)=1/k; 类似，可得 p（k－3）=p(k－4)=…=p（1） =1/k 命题得证。 EX08、写一算法，求 n=12~20 时最优的 StepVegas 值。 ///////////////////////////////////Queen.h class Queen { } } } return false; { count = 0; } bool Queen::QueensLV(int stopVegas) //随机放置 n 个皇后的 Las Vegas 算法 { int k = 1; //随机数产生器 int count = 1; while( (k <= stopVegas) && (count > 0) ) friend bool nQueen(int, int); friend bool nQueen(int n, int stopVegas,int &VistedNodes); int getVistedNodes() { return vistedNodes; } private: //测试皇后 k 置于第 x[k]列的合法性 bool Place(int k); bool Backtrack(int t); //解 n 后问题的回溯法 bool QueensLV(int stopVegas); //随机放置 stopVegas 个皇后 LV 算法 int n; int vistedNodes; //一次搜索成功或失败访问的节点数。 int *x; int *y; //皇后个数 //解向量 }; bool Queen::Place(int k) {//测试皇后 k 置于第 x[k]列的合法性 for( int j=1; j n) { } else { { for(int i=1; i<=n; ++i) { y[i] = x[i]; } return true; for(int i=1; i<=n; ++i) x[t] = i; if( Place(t) && Backtrack(t+1) ) { return true;

} bool nQueen(int n, int stopVegas,int &vistedNodes)//算法：先 LV 后回溯法 { for( int i = 1; i <= n; ++i) { x[k] = i; if( Place(k)) { y[count++] = i; } } if( count > 0 ) { x[k++] = y[rand()%count]; } } return (count>0); //放置成功 Queen X; X.n = n; X.vistedNodes = 0; int *p = new int[n+1]; int *q = new int[n+1]; for( int i=0; i <= n; ++i) { p[i] = 0; q[i] = 0; } X.y = p; X.x = q; bool found = false; while(!X.QueensLV(stopVegas)); if(X.Backtrack(stopVegas+1)) //回溯搜索 { found = true; } delete[] p; delete[] q; vistedNodes = X.vistedNodes; return found; } //////////////hh.cpp #include #include #include #include #include #include"Queen.h" using namespace std; void test() { for( int n=12; n<=20; ++n) { cout<<"皇后个数 n="<

}else{ failVistedNodes += vistedNodes; ++failCount; } } } double p = 10.0/(10.0+failCount); cout< #include #include #include using namespace std; int q=0; bool Btest(int a,int n) { int s=0,t=n-1; int x; do { s++; t=t/2; }while(t%2!=1); for(int j=1;j<=t;j++) x=(x*a)%n; if(x==1||x==n-1) {

分享到：

赞收藏

资料库

中科大算法设计与分析.doc

相关推荐

课程资源

热门标签

最新资料