太阳影子定位模型.pdf-资料库

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第1页.png

第1页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第2页.png

第2页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第3页.png

第3页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第4页.png

第4页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第5页.png

第5页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第6页.png

第6页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第7页.png

第7页 / 共28页

e4a31623-7d80-4d80-9614-7fe57782d2f0.pdf-第8页.png

第8页 / 共28页

太阳影子定位模型摘要针对根据视频中太阳影子变化信息确定拍摄地点和日期的具体问题，可将太阳高度角和太阳方位角作为桥梁，从而建立地理位置及日期时间与太阳影子变化信息相关的数学模型。根据已知数据，将太阳高度角（或太阳方位角）的模型求解值与实际值的吻合程度作为目标函数，将其转化为非线性规划问题，使用遗传算法进行求解，并对结果进行聚类分析。问题Ⅰ，根据确定的地点和日期，计算出每个时刻对应的太阳高度角，进而利用直杆长度和太阳高度角的几何关系计算出 9:00~15:00 内对应的直杆的影子长度。问题Ⅱ，基于直杆长度未知，利用已知的太阳影子顶点坐标，通过几何关系确定太阳方位角。在日期确定的情况下，将经度和纬度作为遗传基因，将太阳方位角匹配程度作为适应度函数，应用遗传算法多次求解。最优结果为（36.5790°N，116.6429°E）。问题Ⅲ，基于直杆长度和日期未知的情况下，将经度、纬度和日期同时作为遗传基因，类似于问题Ⅱ方法，应用遗传算法多次求解。据附件 2 数据可得两地点及对应日期：（29.0360°N，84.6533°E）—7 月 7 日和（29.0964°N，85.4660°E）—6 月 11 日；据附件 3 数据可得两地点及对应日期：（42.1231°N，117.8127°E）—3 月 3 日和（47.2570°N，118.1280°E） —10 月 1 日。问题Ⅳ，为准确测取直杆影长，使用 MATLAB 预处理视频，提取出特定帧图像，经视角转换后，根据已知杆长按比例测算影长。在摄影视角未定的情况下，将太阳高度角作为适应度函数，应用遗传算法，在已知日期的情况下求解得到两地点：（37.9231°N，110.4611°E）和（6.2121°S，123.7418°E）；若日期不确定的情况下，不能确定拍摄地点与日期。最后对模型进行了正确性和灵敏度检验，验证了模型具有较高的准确性和灵敏度，使用遗传算法进行求解，在保证精确度的情况下，大幅度提高了模型求解的速度，为太阳影子定位技术的推广和应用奠定了良好的基础。关键词：太阳影子定位非线性规划遗传算法聚类分析灵敏度分析 1

一、问题重述 1.1 问题背景目前民用手持式定位设备的定位技术主要有三种：基于 GPS 的定位，基于基站定位及小范围内的 Wifi 定位。这三种定位方式都需要利用相应的信号，容易受到电磁场的干扰和测量地建筑群的影响，在信号混杂的环境中难以获得精准的定位。当手持式定位设备不可用时，可以使用太阳定位技术。本文采用太阳影子定位技术，通过分析视频中固定直杆在水平地面上的太阳影子的变化情况，建立数学模型，推算视频拍摄地点的经纬度和拍摄日期。在日照情况良好的情况下，太阳影子定位技术有操作简单、抗干扰能力强的优点。 1.2 问题提出本文基于太阳影子定位技术，研究并建立数学模型，以解决以下问题。问题Ⅰ：建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用你们建立的模型画出 2015 年 10 月 22 日北京时间 9:00-15:00 之间天安门广场（北纬 39 度 54 分 26 秒,东经 116 度 23 分 29 秒）3 米高的直杆的太阳影子长度的变化曲线。问题Ⅱ：根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点。将模型应用于附件 1 的影子顶点坐标数据，求解出若干个可能的地点。问题Ⅲ：根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点和日期。将模型分别应用于附件 2 和附件 3 的影子顶点坐标数据，求解出若干个可能的地点与日期。问题Ⅳ：分析附件 4 的固定直杆（杆高约 2 米）在太阳下的影子变化的视频，在拍摄日期已知和未知两种情况下，分别建立确定视频拍摄地点的数学模型，并应用该模型求解出若干个可能的拍摄地点。 2

二、模型假设与约定 1. 假定直杆与水平地面垂直。 2. 假定摄像机与被摄直杆的位置都是固定的。 3. 假定直杆在水平地面的影子仅仅由于太阳光照形成，不考虑建筑群对太阳光阻挡、空气颗粒物、外界灯源等因素对影子形成的影响。 4. 假设地球为标准球体，均匀自转，忽略平太阳时与真太阳时的差值。 5. 约定以直杆底端为原点；以平行于赤道的方向为轴，东向为轴正方向；以平行于地轴的方向为轴，北向为轴正方向。 3 xxyy

三、符号说明及名词定义表 1 符号说明及名词定义表含义直杆高度直杆在水平地面上的影子直杆影子与水平地面轴的夹角太阳时时角太阳赤纬角 n 为日期序号，表示一年内的第 n 天地理纬度地理经度太阳高度角太阳方位角适应度函数符号 4 hlxstnAf

四、模型准备 4.1 太阳照射的相关物理量 (1) 太阳时  太阳时是指以太阳日为标准来计算的时间。可分为真太阳时和平太阳时。日晷所表示的时间是真太阳时，钟表所表示的时间是平太阳时。我国采用东经 120 度经圈上的平太阳时作为全国的标准时间，即“北京时间”[1]。本文出现的太阳时均为平太阳时，并忽略平太阳时与真太阳时的差值。 (2) 地方时地方时是以观测者的子午线（经线）为基准的时间，与理论时区的时间有一定时差。地理学上，两地经度相差 15 度，则地方时相差 1 小时。东边的时区时间比西边的时区时间来得早。 (3) 时角时角是以正午 12 点为 0 度开始算，每一小时为 15 度，上午为负下午为正，即 10 点和 14 点分别为-30 度和 30 度。因此，时角的计算公式[1]为 (1) 其中为地方太阳时（单位：小时）。 (4) 赤纬角赤纬角也称为太阳赤纬[1]，即太阳直射纬度，其计算公式近似为其中 n 为日期序号，表示一年内的第 n 天。例如，1 月 1 日为，3 月 22 日为 (5) 太阳高度角 (2) 。太阳高度角是太阳相对于地平线的高度角，这是以太阳视盘面的几何中心和理想地平线所夹的角度。太阳高度角可以使用下面的算式，经由计算得到很好的近似值： (3) 其中为太阳高度角，为时角，为当时的太阳赤纬，为当地的纬度[2]。 (6) 太阳方位角 5 ()st()1512stst()228423.45sin365n1n81n()sinsinsincoscoscos()A

太阳方位角是太阳在方位上的角度，它通常被定义为从北方沿着地平线顺时针量度的角 [3]。它可以利用下面的公式，经由计算得到良好的近似值。 (4) 因为公式是使用余弦函数，所以方位角永远是正值，因此，角度永远被解释为小于 180 度，而必须依据时角来修正。当时角为负值时(上午)，方位角的角度小于 180 度，时角为正值时(下午)，方位角应该大于 180 度，即要取该角与 360 度的差值的绝对值。 4.2 遗传算法 1975 年 Michigan 大学的 J.Holland 教授提出“遗传算法”的概念。遗传算法是模拟达尔文生物进化论的自然选择和孟德尔遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法[4]。遗传算法的基本步骤如下： 1）随机初始化种群和染色体； 2）计算种群适应度，选取最优个体； 3）根据种群适应度进行选择、交叉和变异操作； 4）循环计算，直至满足停止准则为止。 6 sinsinsincoscoscosA

五、模型的建立与求解 5.1 模型Ⅰ：影子长度变化模型 5.1.1 问题Ⅰ分析以固定直杆的影子长度为目标函数，建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律。问题Ⅰ中直杆长度已知，所以只需直杆所在处的太阳高度角即可计算出直杆影子的长度。太阳高度角可根据当地的经纬度、当时的日期及太阳赤纬角求得。另外，问题Ⅰ中所给时间为北京时间，即东经 120 度的地方平太阳时，与直杆所在地天安门广场（东经 116 度 23 分 29 秒）的地方时有 14.5 分钟的时差。 5.1.2 模型Ⅰ的建立以某地直杆影子形成的几何示意图为研究对象：图 1 影子形成几何示意图其中，为直杆高度，为影子长度，为当地太阳高度角。所以目标函数为 (5) 由上文模型准备中的式(1)(2)(3)可知：而且 (6) 7 hllhtansinsinsincoscoscos228423.45sin3651512snt12015sstt北京太阳光照αhl

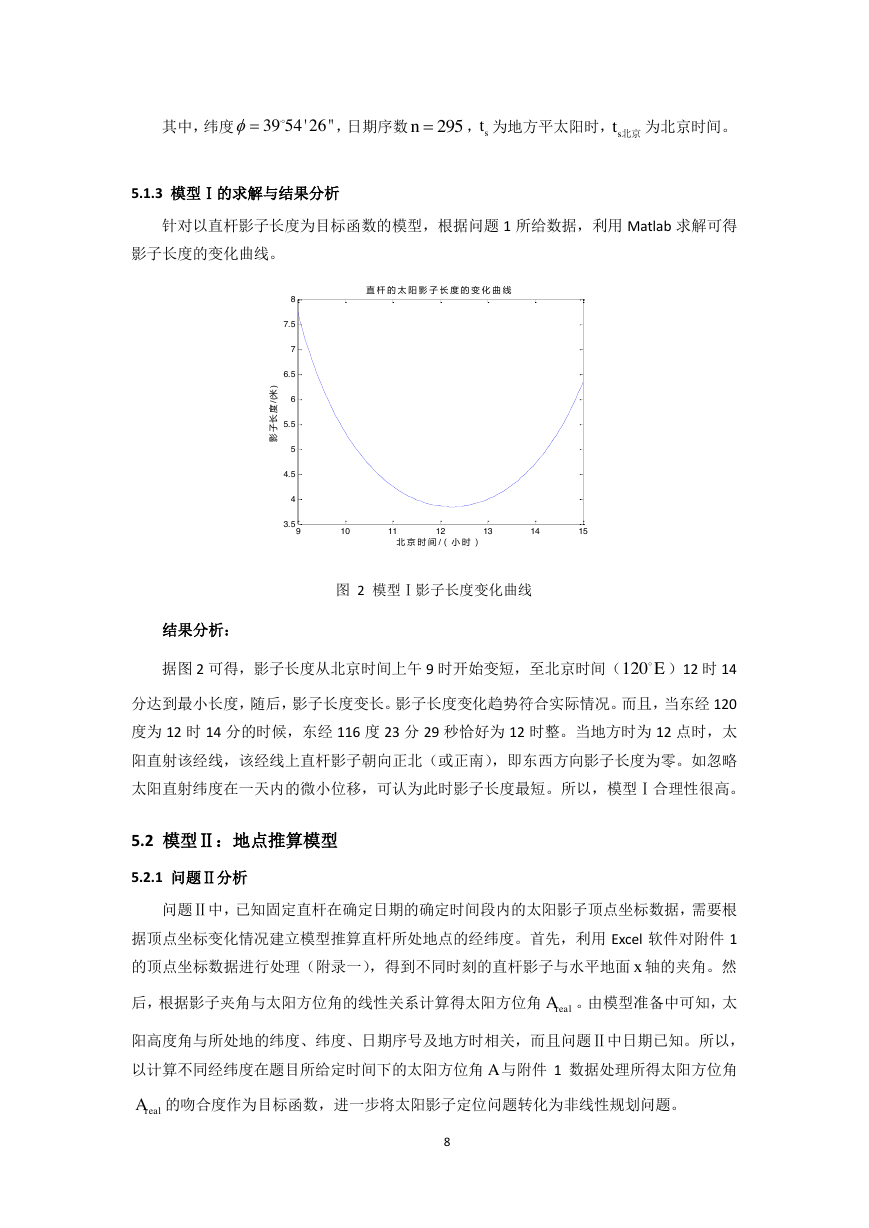
其中，纬度，日期序数，为地方平太阳时，为北京时间。 5.1.3 模型Ⅰ的求解与结果分析针对以直杆影子长度为目标函数的模型，根据问题 1 所给数据，利用 Matlab 求解可得影子长度的变化曲线。图 2 模型Ⅰ影子长度变化曲线结果分析：据图 2 可得，影子长度从北京时间上午 9 时开始变短，至北京时间（）12 时 14 分达到最小长度，随后，影子长度变长。影子长度变化趋势符合实际情况。而且，当东经 120 度为 12 时 14 分的时候，东经 116 度 23 分 29 秒恰好为 12 时整。当地方时为 12 点时，太阳直射该经线，该经线上直杆影子朝向正北（或正南），即东西方向影子长度为零。如忽略太阳直射纬度在一天内的微小位移，可认为此时影子长度最短。所以，模型Ⅰ合理性很高。 5.2 模型Ⅱ：地点推算模型 5.2.1 问题Ⅱ分析问题Ⅱ中，已知固定直杆在确定日期的确定时间段内的太阳影子顶点坐标数据，需要根据顶点坐标变化情况建立模型推算直杆所处地点的经纬度。首先，利用 Excel 软件对附件 1 的顶点坐标数据进行处理（附录一），得到不同时刻的直杆影子与水平地面轴的夹角。然后，根据影子夹角与太阳方位角的线性关系计算得太阳方位角。由模型准备中可知，太阳高度角与所处地的纬度、纬度、日期序号及地方时相关，而且问题Ⅱ中日期已知。所以，以计算不同经纬度在题目所给定时间下的太阳方位角与附件 1 数据处理所得太阳方位角的吻合度作为目标函数，进一步将太阳影子定位问题转化为非线性规划问题。 8 3954'26''295nstst北京120ExrealAArealA91011121314153.544.555.566.577.58北京时间/（小时）影子长度/(米)直杆的太阳影子长度的变化曲线

资料库

太阳影子定位模型.pdf

相关推荐

行业

热门标签

最新资料