logo资料库

论文研究-风险价值的完全参数方法及其在金融市场风险管理中的应用.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.20M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    Λ 系统工程理论与实践 第 4 期　 0074 06 2 2 α 　2001 年 4 月 文章编号: 1000 6788 (2001) 04 风险价值的完全参数方法及其在金融市场风险管理中的应用 马超群1, , 李红权1, 徐山鹰2, 杨晓光2, 李　晖1 (1. 湖南大学工商管理学院, 湖南 长沙 410082; 2. 中国科学院管理、决策与信息系统开放研究实验室, 北京 100080) at 摘要: 　风险价值模型 (V alue R isk) 是近年来发展起来的用于测量和控制金融风险的量化模型 本文提出了计算风险价值的一种新方法——完全参数方法, 它本质上是参数方法和极值理论的结合 运用, 在证券市场上的实证研究表明该方法优于目前流行的 R iskM etrics 这种参数方法 关键词: 　风险价值; 完全参数; 风险管理; 金融市场 中图分类号: 　F830. 9　　　　　文献标识码: 　A 　　 To tal p aram etric M ethods of V aR and Its A pp lication s in R isk M anagem en t of F inancial M arket M A Chao qun 1, 2, L I Hong YAN G X iao guang2, L I H u i1 quan 1, XU Shang ying2, (1. Co llege of B u siness M anagem en t, H unan U n iversity, Changsha 410082, Ch ina; 2. L abo rato ry of M anagem en t, D ecision and Info rm ation System s, Ch inese A cadem y of Sciences, B eijing 100080, Ch ina) at Abstract: 　V alue R isk m odel develop ed recen tly is a m athem aticalm odel to m easu re and m on ito r m arket risk. T h is article p u ts fo rw ard a new m odel called to tal p aram etric m ethod to calcu late V aR , w h ich is in essence the m ix tu re of p aram etric m ethod and ex trem e value theo ry. R esearch on stock m arket show that th is new m odel gain s an advan tage over R iskM etrics w h ich is a pop u lar p aram etric m ethod. Keywords: 　 V alue m arket p aram etric m ethod; risk m anagem en t; financial at R isk; to tal R isk) , 已得到广泛的 　　近年来, 新出现的金融风险管理工具——风险价值方法或称V aR 方法 (V alue 在美国, 三十小组 (T he Group of T h irty) , 衍生产品小组 (the D erivatives P roduct Group ) , 国 重视和应用 际互 换 与 衍 生 品 协 会 ( the In ternational Sw ap s and D erivatives A ssociation )、国 际 清 算 银 行 (B ank of In ternational Settlem en ts) 以及欧盟 (Eu rop ean U n ion) 等都在一定程度上将V aR 作为风险度量的标准 在 国内, V aR 方法也引起了金融机构和学者的注意, 这一方面的研究刚刚起步 由于经济全球化的影响, 特别 是自 70 年代初布雷顿森林体系崩溃以来, 汇率、利率等金融产品价格的变动日益趋向频繁和无序, 金融市 场上的风险与日俱增 采用新的、更全面的技术, 加强金 融市场风险管理, 已是我国各金融机构和金融当局的当务之急 刚刚过去的东南亚金融危机就是一个沉重的警钟 at 1　风险价值的本质及基本算法 V aR 方法简言之是用来测量给定投资工具或组合在未来资产价格波动下可能或潜在的损失. Ph ilipp e ”在数 Jo rion 1 给出的权威说法是“在正常的市场条件下, 给定置信区间的一个持有期内的最坏的预期损失 收稿日期: 2000 资助项目: 国家自然科学基金“九五”重点项目 (G79790130) 09 05 © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
    Ρ Ζ Α Κ Λ Κ ØΡ Ø Α Α 第 4 期 风险价值的完全参数方法及其在金融市场风险管理中的应用 57 学上, 它表示为投资工具或组合的损益分布(P & L distribu tion) 的 分位数 ( - quartile) , 表达式为: △p △t 表示组合 p 在△t 持有期内在置信度 (1- V aR 的概率为 是 , 或者可以说, 在概率 的函数, 若以 F (△p △t) 表示资产组合收益的概率分布函数, 那么有: P r (△p △t ≤- V aR ) = ) 下的市场价值变化 下, 损失值是大于V aR 的 (1) 等式 (1) 说明了损失值等于或大于 在后一种解释中, 我们其实把V aR 看做 V aR = F - 1 ( 或者, 直接由其定义出发, 我们可以以下式来计算风险价值: ) (2) ) 对于市场风险而言, 考虑的持有期一般很短, 于是可以假设 V aR = E (w ) - w = w 0 (1 + E (R ) ) - w 0 (1 + R = w 0 (E (R ) - R ) E (R ) = 0　 这样 V ar = - w 0R E (w ) 表示投资工具或组合在持有期末的期望价值; w 0 表示持有期初资产组合的价值; w 最低资产组合价值; E (R ) 表示在整个持有期间的期望收益率; R 表示一定置信度C 下的最低资产收益率 由此可知, 风险价值方法的核心在于如何确定 F (△p △t) 即资产组合收益的概率分布函数, 亦即如何 围绕这一问题的解决产生了两大类方法: 参数方法、模拟方法 (可分为历史模拟法和蒙特卡 (3) 表示一定置信度 C 下的 或w 确定 R 罗模拟法) 1. 1　模拟方法 历史模拟法 (H isto rical sim u lation m ethod, 简称 H S 法) 是借助于计算过去一段时间内的资产组合风 险收益的频率分布, 通过找到历史上一段时间内的平均收益, 以及既定置信水平下的最低收益水平, 推算 V aR 的值, 其隐含的假定是历史变化在未来可以重现 从以上可知, 历史模拟方法 (H S) 是基于历史数据的经验分布, 它不需对资产组合价值变化的分布作特 定假设 该方法简单、直观、易于操作 但同时 H S 法也有很多缺陷 趋势发生逆转时, 基于原有数据的V aR 值会和预期最大损失发生较大偏离 (a bad estim ato r) 能提供比所观察样本中最小收益还要坏的预期损失 一个较大的方差 具体表现在: 第一, 收益分布在整个样本时限内是固定不变的, 如果历史 第二, H S 不 第三, 样本的大小会对V aR 值造成较大的影响, 产生 第四, H S 不能作极端情景下的敏感性测试 M on te Carlo 方法与 H S 十分类似, 它们的区别在于前者是基于历史数据或既定分布假定下的参数特 征, 借助随机方法模拟出大量的资产组合数值, 从中推出V aR 值, 这种方法有广阔的应用前景 1. 2　参数法 (亦称方差-协方差法, Var iance-covar iance m ethod) 这种方法的核心是基于对资产报酬的方差 协方差矩阵进行估计 其中最具代表性的是目前流行使用 的 J. P. M o rgan 银行的 R iskM etriceTM 方法, 它的重要假设是线性假设和正态分布假设, 详见文献 3, 7 即x- = 0, 即 X ～ N (0, ～ N (0, 1) , 且设 2) 获取方差 可以通过两种方式, 一种是等权重方式 (equally m oving average app roach) , 它度量的是无 条件波动 (unconditional vo latility) , 即 = n 1 n - 1 t= 1 (R t - ) 2; 另一种是指数权重计算方式 (exponen tially w eigh ted m oving average app roach) , 它度量的是有条件波 动 (conditional vo latility) , 这种方法被 R iskM etrics 所采用, 表达式如下: n t= 1 = (1 - ) V aR = Z w 0 n- t (R t - ) 2 (4) (5) 其中, Z 表示标准正态分布的 分位数 © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
    5 ΛΡ Α Α Α Α Α Α 67 系统工程理论与实践 2001 年 4 月 即对距离现在时点较近的数据赋予较大的权重 它能较好地反映金融时间序列波动的一些特性, 如集 = 0. 97, 它本质上是 GA RCH 模型, h t= t- 1, 即方差是滞后项与过去误差的函数, 较好地解决了条件异方差现象, 对预测正常的、温 2 丛行为 (clu stering behaviou r) h t- 1+ (1- 和的波动很有价值, 但在预测极端事件或突变方面仍不尽人意 = 0. 94; 对每月数据, 对每日数据, ) 2　风险价值方法的改进——完全参数方法 (Tota l-param etr ic m ethod) V aR 分析是针对下偏风险的, 即损失边, 因而极端收益情景的准确预测对V aR 的计算有着极其重大 然而, 历史模拟法或参数法虽对概率分布函数的中间部位即对正常的、温和的波动有着较好的预 而极值理论 (Ex trem e V alue T heo ry, 简称 EV T ) 恰恰弥补 极值理论研究的重点就是极端情况下收益波动的特征及分布形态, 对极端情景有很好的 所以, 将极值理论和历史模拟方法或参数方法结合运用应该对风险价值将有更好的估测能力 的意义 测能力, 但对极端收益情景提供的信息极有限 了这一重大缺陷 预测能力 本文着重介绍一下 EV T 和参数法 (unconditional) ①综合运用的情况 2. 1　极值理论与尾部估计量 限于篇幅, 本文只介绍极值理论最新的发展成果 4, 5 . 1) H ill(1975) 提出 F (x ) 可以近似由一阶展开式模拟 F (x ) = P r (X > x ) = ax - 　　a > 0, x → ∞ H ill 还给出了 的一阶矩估计量 = 1 M M i= 1 lnX (i) - lnX M + 1 - 1 　　X (i) > X (M + 1) (6) (7) X (i) 表示样本中第 i 个降序统计量;M 表示临界样本序号, 其意义在于, 当 X > X (M + 1) 时, ax - P r (X > x ) 近似地等于 2) D an ielsson, devries (1997) 提出了确定 、X p、P 的新方法 1 = 1 M M i= 1 ln X i xM + 1 X = X M + 1 1 M nP P = M n X M + 1 X P (8) (9) (10) 由上面可知, 关键问题在于如何确定 X M , 这一临界值的的含义是从第M 个统计量开始, X 1、X 2, …, X M 这 些数据 (降序统计量) 用来估计 - M 图) ; 另一种是计算 机优化方法 2. 2　完全参数方法 选择M 、X M 值的方法有二种, 一种是作图法 (做 本文采用简单有效、易于操作的第一种方法 其核心思想是: 在收益率序列下尾部的变量 X < X M low er+ 1= X S 时, 我们用极值理论所提出的分布函数 来近似描述 P r (X > x ) ; 对于上尾部而言, 也存在着一个临界值 X S ′, 当 X > X S ′时 P r (X > X S X F (x ) = M n x ) 近似等于M ′ 值可能不为 0, 本文释放了 R iskM etricsTM 中 X S X n ′ ; 对于处于两者中间的部分, 即 X S < X < X S ′时, 用正态分布去做 考虑到收益率的均 = 0 的假设条件 该方法的概率分布函数为: M n X M low er+ 1 X X < X M low er+ 1 F (x ) = x - X M low er+ 1 ≤ X ≤ X M upper+ 1 (11) 1 - M ′ n X M upper+ 1 ′ X X > X M upper+ 1 ① 参数法 (unconditional) 对方差的处理是运用等权重方法 © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
    Λ 3 3 Ζ Α Ζ Λ 77 第 4 期 风险价值的完全参数方法及其在金融市场风险管理中的应用 X P 表示 P 函数关系式为: X M low er+ 1 X P = + Z P 1 M low er np M low er + 1 P < n M low er + 1 n ≤ P ≤ 1 - M upper + 1 n (12) X (M upper + 1) 1 ′ M upper n - np P > 1 - M upper + 1 n 表示 标准正态分布函数表达式的简写; Z p 表示标准正态分布的 p 分位数; X (np ) 表示收益序列 X 的第 np 个升序统计量; X (MM up p er+ 1)、 ′、M upper均是描述上尾部的统计量 分布函数的性质 性质 1　　　　　　　F (+ ∞) = lim x →+ ∞ 1- M ′ n X M upper+ 1 X ′ = 1 　　性质 2　　　　　　F (+ ∞) = lim x →+ ∞ M n X M low er+ 1 X = 0 性质 3　F (x ) 有两个间断点, X 1= X M low er+ 1, X 2= X M upper+ 1 如果 X 是收益率序列, 则 X P 就是所要求的 R 投资工具或组合的 V aR 表达式为: V aR (c) = - W 0X p 　　P = 1 - c 3　实证研究 (13) (14) (15) 本文以证券市场为应用研究的对象, 取上证综指 (IA 0001) 作为样本① 原始样本, 即用来预测 V aR 值 31, 样本数 n1= 494; 检验样本②, 即用来检验, 比较各种模型准确性的 由于上证综指已经包含了除权信息, 所以投资工具的 07, 样本数 n2= 484 取 1997 的母样本 样本, 取 1998 收益率可简单地表示为 01 07 07- 2000 07 02- 1998 12 　　由于正态分布假定是 R iskM etricsTM 的一个重要前提条件, 也是争论比较多的假设 1, 2, 4, 6 , 本文先进行 正态分布为原假设的检验 结果如表 1: R t = P t - P t- 1 P t- 1 (16) 表 1　正态分布检验表 偏斜度 (S ) 峰态值 (K ) 统计量 (L ) H 0: 正态分布 原始样本 检验样本 - 0. 0153 0. 00496 10. 604 9. 095 1187. 78 746. 103 拒绝 拒绝 　　L～ 2 (2) 　临界值L L = 5. 99 (95% 置信度) = 10. 579 (99. 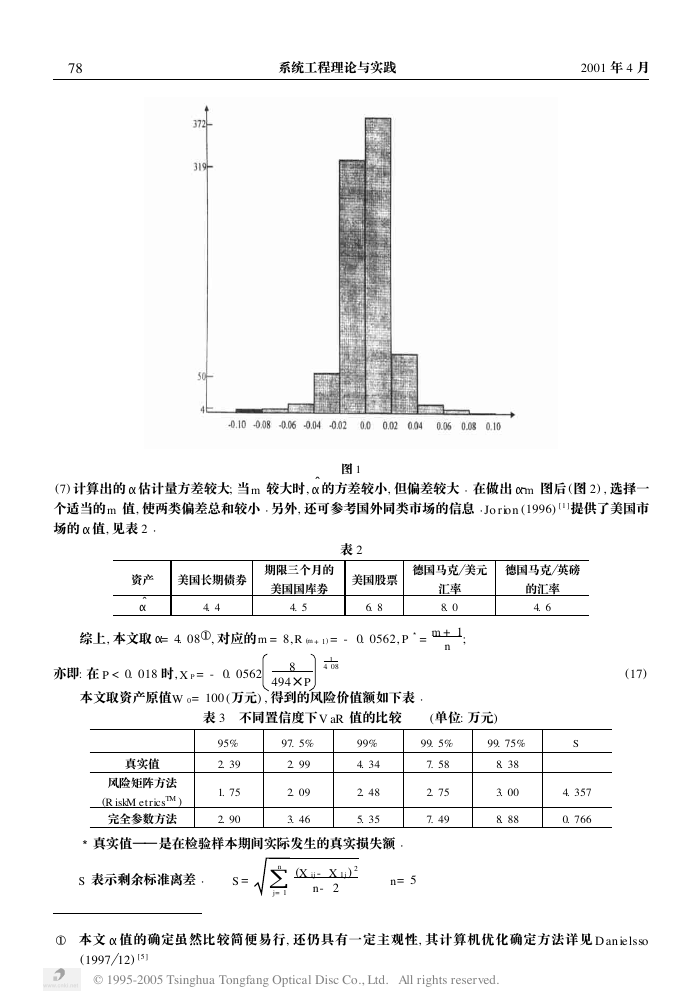5% 置信度) 所以, 本文有充分的把握认为正态分布的假定不够贴近现实收益波动状况 布基本上无偏, 而 K 值较大, 说明收益分布有典型的“细腰”、厚尾之特证 (正态分布, K = 3) 01 02- 2000 正是因为 R iskM etricsTM 的基本假设与实际不符, 所以才会产生较大误差, 特别是在置信度较大的情况下 本文介绍的新方法可以弥补这一缺陷 如前所述, 该方法关键问题是如何选择 07 的收益率频率直方图如下: 当m 较小时, 用式 值 07 另外, 从 S 值上看, 收益分 全样本 1997 在这里, 我们实际上将上证综指作为一种投资工具, 或是一种“虚拟”的股票的价格 ① ② 原则上, 检验样本应是一种全新数据样本, 但由于本文数据来源有限, 故有所重叠, 但这并不影响结论 的正确性 © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
    Ζ Α Ù 87 3 系统工程理论与实践 2001 年 4 月 估计量方差较大; 当 m 较大时, (7) 计算出的 个适当的m 值, 使两类偏差总和较小 场的 值, 见表 2 在做出 m 图后 (图 2) , 选择一 Jo rion (1996) 1 提供了美国市 图 1 的方差较小, 但偏差较大 另外, 还可参考国外同类市场的信息 表 2 资产 美国长期债券 期限三个月的 美国国库券 美国股票 德国马克 汇率 4. 4 4. 5 6. 8 8. 0 美元 德国马克 英磅 的汇率 4. 6 　　综上, 本文取 = 4. 08①, 对应的m = 8, R (m + 1) = - 0. 0562, P 亦即: 在 P < 0. 018 时, X P = - 0. 0562 1 4. 08 8 494×P 本文取资产原值W 0= 100 (万元) , 得到的风险价值额如下表 = m + 1 ; n 表 3　不同置信度下V aR 值的比较　　 (单位: 万元) (17) 真实值 风险矩阵方法 (R iskM etricsTM ) 完全参数方法 95% 2. 39 1. 75 2. 90 97. 5% 2. 99 2. 09 3. 46 99% 4. 34 2. 48 5. 35 99. 5% 99. 75% S 7. 58 2. 75 7. 49 8. 38 3. 00 8. 88 4. 357 0. 766 　　 真实值——是在检验样本期间实际发生的真实损失额 S 表示剩余标准离差 　　S = n j= 1 (X ij - X 1j) 2 n- 2 　　 n= 5 ① 本文 (1997 值的确定虽然比较简便易行, 还仍具有一定主观性, 其计算机优化确定方法详见 D an ielsso 12) 5 © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
    Λ Λ 第 4 期 风险价值的完全参数方法及其在金融市场风险管理中的应用 Λ 97 为了能够更清晰、明了地看出每种方法预测的精度, 本文将列出误差比较分析表, 如表 4 表 4　不同计算方法的误差比较分析 置信度 U ij 方法 95% 97. 5% 99% 99. 5% 99. 75% 风险矩阵法 完全参数方法 - 26. 8% 21. 3% - 30. 1% 15. 7% - 42. 9% 23. 3% - 63. 7% - 1. 2% - 64. 2% 6. 0% 45. 5% 13. 5% 　　 U ij表示误差; U ij = X ij- X 1j X 1j ; 表示离差均值; = U ij n ; 图 2　 m 图 图 3　几种分布的下尾部 (局部) 比较图 　　 根据以上各表、图可知: 由表 3, 完全参数方法的剩余标准离差 S = 0. 766< 4. 357, 说明此方法提供的 V aR 预测值与实际损失 值差异较小, 对现实波动情形拟合要比 R iskM etricsTM 为好 由表 4, R iskM etricsTM 均低估了实际损失值, 特别是在置信度较高时, 低估倾向愈大 而完全参数方法在 而 R iskM etricsTM 的较差表现是与其正态分布的 高置信度时表现尤佳, 这说明极值分布对现实拟合较好 假设密切相连的, 这造成了必然的低估倾向, 这一点在图 4 的下尾部分布比较图上一目了然 之所以 R iskM etricsTM 是流行使用的方法, 部分是因为国外许多银行用这一模型来决定存款准备金的数额, 它们普通 不希望存款准备金过多, 因而青睐这种低估V aR 值的方法 因此, 许多银行都低估了自身面临的风险, 一旦 某些高风险投资项目失败, 较低的存款准备金将使银行无法应付这种危险局面, 从而可能引发破产危机 完全参数方法的分布函数在下尾部是光滑连续的, 这有利于作敏感性分析等 此外, 这种方法还有超 越样本范围作出准确预测的优点 4　结论 如参量法、历史模拟法和随机模拟法 (蒙太卡罗法) 都是遵循这一思路进行的 本文引入了计算V aR 的一种新的方法, 并对极值理论做了深入、全面的讨论 实证研究的结果表明这 新方法能准确地反映金融机构面临的市场风险, 有利于深层次、全面 种新方法要优于 R iskM etricsTM 方法 然面, 需要指出的是 V aR 是基于金融资产的客观概率, 也就是说它对金融资产或投资组 地管理金融风险 合的风险计算方法是依据过去的收益特征进行统计分析来预测其价格的波动性和相关性, 从而估计可能 的最大损失 由于完整的金 融风险管理包括风险的识别、测定和控制三个过程, 而且对一定量风险进行控制是金融风险管理的最终目 的, 这必然要涉及风险管理者的风险偏好和风险价格因素 所以单纯依据风险可能造成损失的客观概率, 因为概率不能反映经济主体本身对于面临的风险 只关注风险的统计特征, 并不是系统的风险管理的全部 的意愿或态度, 它不能决定经济主体在面临一定量的风险时愿意承受和应该规避的风险的份额 而完整的 风险管理不但要能计量出面临的风险的客观的量, 而且应该考虑风险承担主体对风险的偏好, 这样才能真 正实现风险管理中的最优均衡 © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved. (下转第 110 页)
    011 系统工程理论与实践 2001 年 4 月 划分有利与人力资源专业特长的发挥 2) 按资源划分——即产生或使用同一类信息资源的人员可划分为相同的角色类, 这样的划分有利于 从资源管理的角度对人员进行管理和分配 3) 按地域划分——在相同地理位置上分布的功能可由同一类角色成员负责, 这有利于系统人员的合 理调度 参考文献: 1 　V o ss K. N ets in office au tom ation[J . L ectu re N o tes in Com p u ter Science, 1986, 340: 234- 257. 2 　V o ss K. PetriN ets fo r Info rm ation System M odeling[J. L ectu re N o tes in Com p u ter Science, 1995, 935: 23- 37. 3 　T aubner D. O n the Im p lem en tation of Petri N ets [J . L ectu re N o tes in Com p u ter Science, 1986, 340: 418- 439. 4 　袁崇义. Petri 网[M . 南京. 东南大学出版社. 1989. 5 　王景光. 基于 Petri 网的信息系统建模与分析[D . 北京理工大学博士论文. 1999. (上接第 79 页) 金融风险管理理论最新进展即 TRM 系统就是在现有风险管理系统的单一变量, 即概率 (P robab ilities) 的 基础上引进另外两个要素, 即价格 (P rices) 和偏好 (P references) , 谋略在三要素 (3P’s) 系统中达到风险管 理上客观量的计量与主体偏好的均衡最优 这样不但可以对基础金融工具风险进行管理, 而且也可以管理 衍生工具可能带来的风险, 从而实现对风险的全面控制 三个要素在 TRM 系统中都是关键性的: 价格是经 济主体为规避风险而必须支付的金额; 概率用来衡量各种风险 (包括衍生交易本身风险) 的可能性, 而偏好 决定经济主体愿意承担和应该规避的风险的份额 金融活动本身涵含的不确定性和风险较大; 对于我国而言, 处于转轨期的市场经济, 风险日益突显, 特 别是在国际经济、金融一体化的以及金融创新工具日新月异的今天, 对我国的金融风险管理又提出了新的 挑战 所以, 及早采用先进、科 学的手段加强金融风险管理, 将是我国金融市场建设的必由之路 随着我国加入W TO 的进程日益加快, 届时开放金融服务业也是大势所趋 参考文献: 1 　Jo rion P. R isk: M easu ring the risk in value at risk [J . D ecem ker 1996: 47- 45. F inancial A nalysts Jou rnal, N ovem ber 2 　B eder T S. V aR: Seductive bu t dangerou s [J . F inancial A nalysts Jou rnal, Sep tem ber O ctober, 1995, 51 (5) : 12- 24. 3 　M o rgan J P. R isk M etrics T echn ical Docum en t [M , N ew Yo rk, 1996. 4 　Jon D an ielsson, Casp er G de V ries. B eyond the sam p le: ex trem e quan tile and p robab ility estim ation [BD OL . www. risk research. o rg, 1997. 5 　 Jon D an ielsson, Casp er G de V ries. V alue at risk and ex trem e retu rn s [BD OL . www. risk risearch. o rg , 2000 6 　王春峰, 万海晖, 张维. 金融市场风险测量模型——V aR [J. 系统工程学报, 2000, (1) : 67- 75. 7 　马超群, 李红权. V aR 方法及其在中国金融风险管理中的应用[J. 系统工程, 2000, 20 (2) : 56- 59. © 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料