论文研究-16QAM调制解调技术分析与MATLAB仿真 .pdf-资料库

5 10 15 20 25 30 35 中国科技论文在线 http://www.paper.edu.cn 16QAM 调制解调技术分析与 MATLAB 仿真李瑞，明洋** （长安大学信息工程学院，西安 710064）摘要：正交幅度调制 QAM （Quadrature Amplitude Modulation）是一种功率和带宽相对高效的信道调制技术，广泛应用于数字电视，无线宽带等传输领域。本文针对 16QAM 系统调制解调系统，利用 MATLAB 工具对整个系统进行完整仿真，并通过星座图仿真对误码率进行分析。仿真结果表明该系统简单可行，对 QAM 相关产品研发和理论研究具有一定的理论和实践意义。关键词：16QAM；正交振幅调制；MATLAB；误码率中图分类号：TN92 无线通信 Analysis and simulation of 16QAM modulation and Demodulation Technology Based on the MATLAB Li Rui, Ming Yang (Department of Information Engineering,Chang'an University, Xi'an 710064) Abstract: Quadrature amplitude modulation (QAM) is a channel modulation techniques with relatively high efficiency of usage power and bandwidth, It is widely used in digital television, broadband and wireless transmission fields. This article in view of the 16 QAM system demodulation system,Then, Use of MATLAB tools to complete the whole system simulation,And through the constellation chart simulation analysis of the ber(bit error rate). Simulation results indicate that this system is both simple and feasible, It has a certain theoretical and practical significance that does the research about products related to QAM. Keywords: 16QAM; Quadrature Amplitude Modulation; MATLAB; Bit Error Rate 0 引言随着移动用户数量的增加和人们对多媒体通信业务要求的提高，需要在有限的带宽里要传输大量的多媒体数据，提高频带利用率成为至关重要的课题。如何在有限的频谱资源中提高容量而且满足数据的高速传输，确定一种高频带利用率的调制方案能在很大程度上解决上述问题。正交振幅调制（QAM，Quadrature Amplitude Modulation）是一种具有高频带利用率，且可以根据传输环境和传输信源的不同，自适应的去调整其调制速率的调制技术，因此能更好的缓和可用频带紧张状况及实现多速率的多媒体综合业务传输[1～2]。目前 QAM 调制技术在国内外颇受关注，主要应用于数字电视这样的宽带系统中，在无线窄带系统的应用范围非常有限。而且研究的焦点集中在解调算法中的载波提取环节，几乎没有针对 QAM 系统级的研究。本文设计的这款 QAM 调制器是针对整个 QAM 调制系统，分析了完整的调制解调过程，并使调制信号通过高斯随机信道，来仿真其通信系统。作者简介：李瑞，（1987-），女，研究生，无线通信，公钥密码学。通信联系人：明洋，（1979-），男，副教授，公钥密码学，可证明安全理论，无线网络安全。 E-mail: yangming@chd.edu.cn - 1 -

40 45 50 55 60 65 中国科技论文在线 1 基础知识 1.1 QAM 的基本概念 http://www.paper.edu.cn QAM 是用两个独立的基带数字信号对两个相互正交的同频载波进行抑制载波的双边带调制。其输出的单频信号是由两个相互正交的 I 信号和 Q 信号组成，其幅度和相位均受到了调制，星座图上每一点对应着一个合成矢量在每一瞬间的输出，即将二进制输出序列映射成了空间上不同的振幅，不同相位的信号波形，所以它是一种多进制的相位、振幅混合调制。它具有较高的信息传输率和频带利用率[3]。MQAM 的时域表达式为 tY )( = tQtI )( )( + = A m sin( ft 2 π + ) B m cos( ft 2 π ) (1) 1.2 16QAM 的调制解调原理 16 进制的正交振幅调制是一种振幅相位联合键控信号。它有正交调幅法和复合相移法有 2 种产生方法。这里采用正交调幅法，用串/并变换器将数据流分成两个半速率（1/2R）数据流，分别进入各自的进制转换器中，按预选设置的多进制转换中任意一种做进制的转化，变成符号速率降低了 2 倍的 2 进制单系列脉冲（此时，符号速率为），将两部分符号频率为 NR 的数字脉冲调制到一对正交的载波上，分别得到 I 信号（同相载波）和 Q 信号（异相载波）[4]。加法器对输入的 I 和 Q 已调波进行线性叠加后，送出 Y(t)=I(t)+Q(t) 合成信号。Y(t)即为已调的 16QAM 信号。MQAM 存在四相相位模糊问题，这里使用 2 相差分编码克服 4 相相位模糊。对多电平信号进行检测并恢复成二进制码时采用了格雷编码技术因其电平逻辑比自然码电平逻辑具有更好的误码特性。解调实际是调制的逆过程，在理想情 M(b/s/Hz),当收发基带滤波器合成相应为滚降因子为况下，MQAM 信号的频带利用率为 log2 M/(1+α)(b/s/Hz)。16QAM 信号 α的升余弦滚降滤波器时，MQAM 信号的频带利用率为 log2 采取正交相干解调的方法解调，解调器首先对收到的 16QAM 信号进行正交相干解调，一 R/2log R = N 2 N cos wct 相乘，一路与路与乘法器产生的高频分量，获得有用信号，LPF 输出经抽样判决可恢复出电平信号。 2 16QAM 的仿真相乘。然后经过低通滤波器，低通滤波器 LPF 滤除 sin wct 2.1 16QAM 调制系统仿真仿真第一部分是信源的产生：信源为随机二进制序列，采用 0 1 单极性不归零波形。这是一种最常用的基带信号形式，其特点是极性单一，有直流分量，脉冲之间无间隔，另外位同步信息包含在电平的转换之中，当出现连零序列时没有位同步信息[5]。信源的仿真是利用 randint（1，N）随机产生 N 列二进制 0 1 序列，再通过阶跃函数产生波形（为了方便观察只列出 16 位码元），仿真结果如图 1 所示 - 2 -

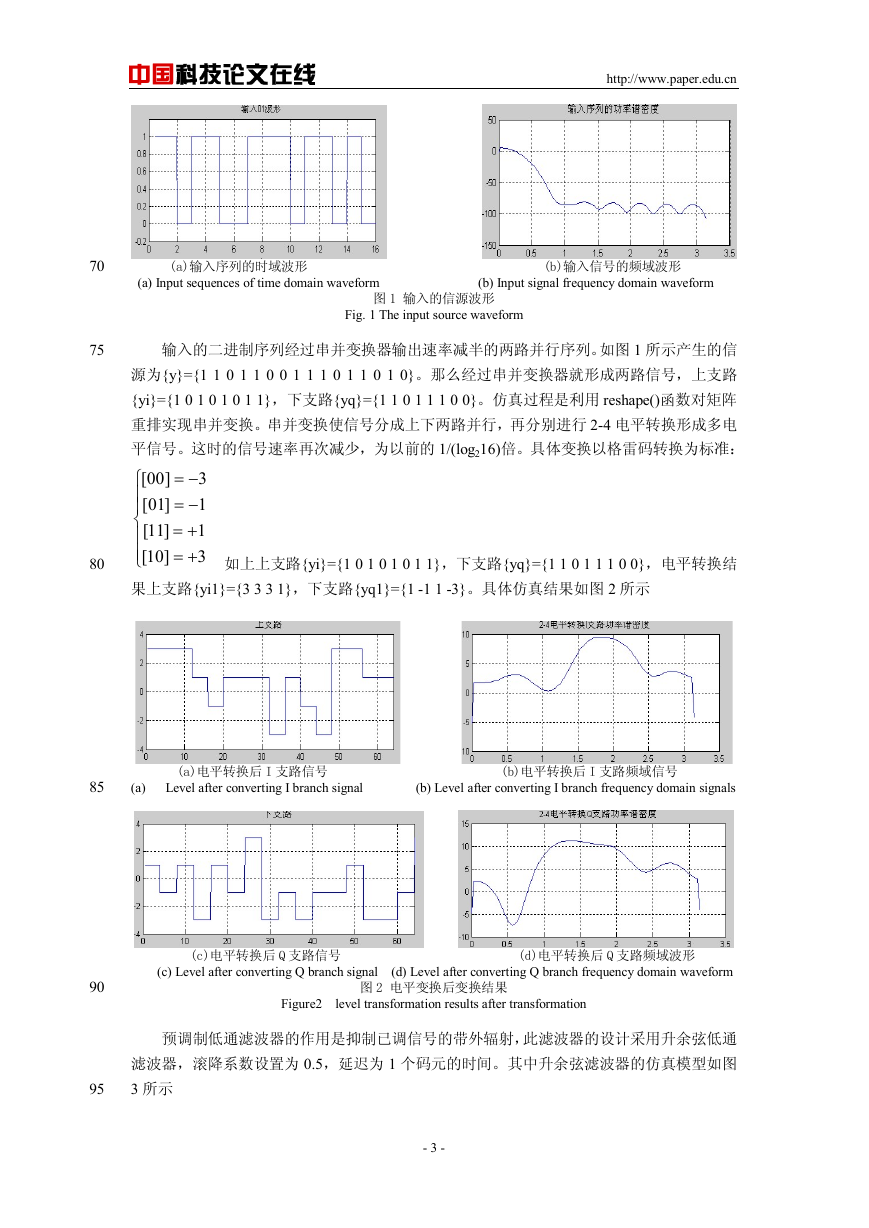
中国科技论文在线 http://www.paper.edu.cn (a)输入序列的时域波形 (b)输入信号的频域波形 (a) Input sequences of time domain waveform (b) Input signal frequency domain waveform 图 1 输入的信源波形 Fig. 1 The input source waveform 输入的二进制序列经过串并变换器输出速率减半的两路并行序列。如图 1 所示产生的信源为{y}={1 1 0 1 1 0 0 1 1 1 0 1 1 0 1 0}。那么经过串并变换器就形成两路信号，上支路 {yi}={1 0 1 0 1 0 1 1}，下支路{yq}={1 1 0 1 1 1 0 0}。仿真过程是利用 reshape()函数对矩阵重排实现串并变换。串并变换使信号分成上下两路并行，再分别进行 2-4 电平转换形成多电平信号。这时的信号速率再次减少，为以前的 1/(log216)倍。具体变换以格雷码转换为标准： ]00[ ⎧ ⎪ ]01[ ⎪ ⎨ ]11[ ⎪ ⎪ ]10[ ⎩ 果上支路{yi1}={3 3 3 1}，下支路{yq1}={1 -1 1 -3}。具体仿真结果如图 2 所示如上上支路{yi}={1 0 1 0 1 0 1 1}，下支路{yq}={1 1 0 1 1 1 0 0}，电平转换结 3 −= 1 −= 1 += 3 += (a)电平转换后 I 支路信号 (b)电平转换后 I 支路频域信号 (a) Level after converting I branch signal (b) Level after converting I branch frequency domain signals (c)电平转换后 Q 支路信号 (d)电平转换后 Q 支路频域波形 (c) Level after converting Q branch signal (d) Level after converting Q branch frequency domain waveform 图 2 电平变换后变换结果 Figure2 level transformation results after transformation 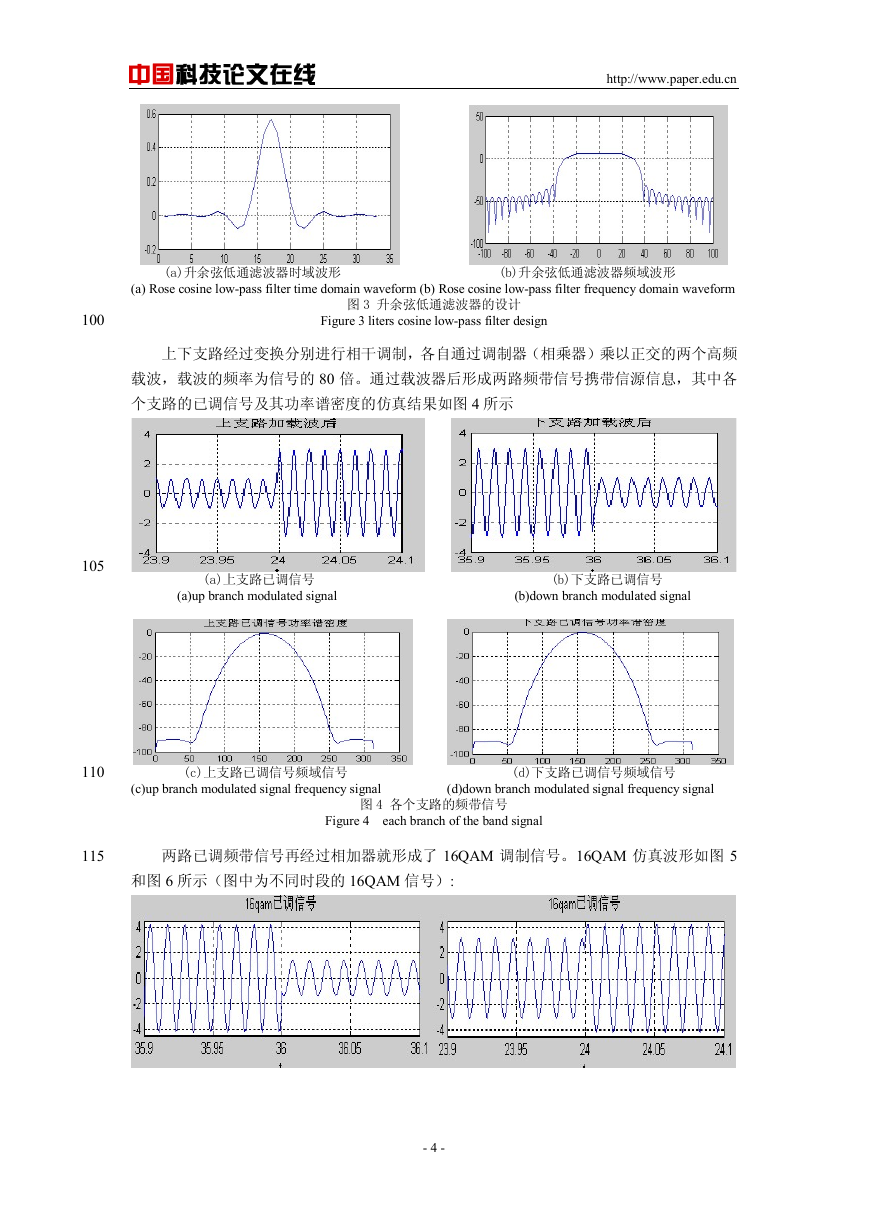预调制低通滤波器的作用是抑制已调信号的带外辐射，此滤波器的设计采用升余弦低通滤波器，滚降系数设置为 0.5，延迟为 1 个码元的时间。其中升余弦滤波器的仿真模型如图 3 所示 - 3 - 70 75 80 85 90 95

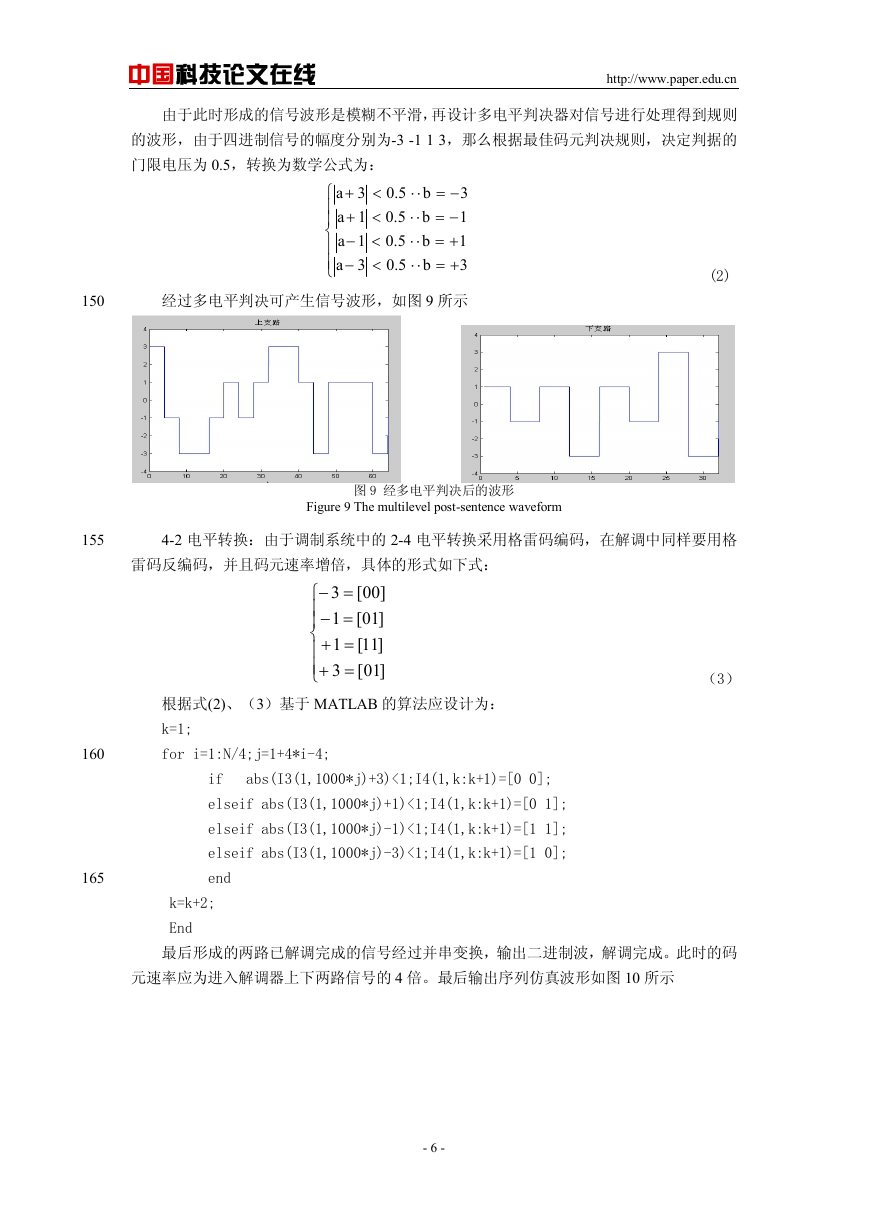
中国科技论文在线 http://www.paper.edu.cn (a)升余弦低通滤波器时域波形 (b)升余弦低通滤波器频域波形 (a) Rose cosine low-pass filter time domain waveform (b) Rose cosine low-pass filter frequency domain waveform 100 105 110 图 3 升余弦低通滤波器的设计 Figure 3 liters cosine low-pass filter design 上下支路经过变换分别进行相干调制，各自通过调制器（相乘器）乘以正交的两个高频载波，载波的频率为信号的 80 倍。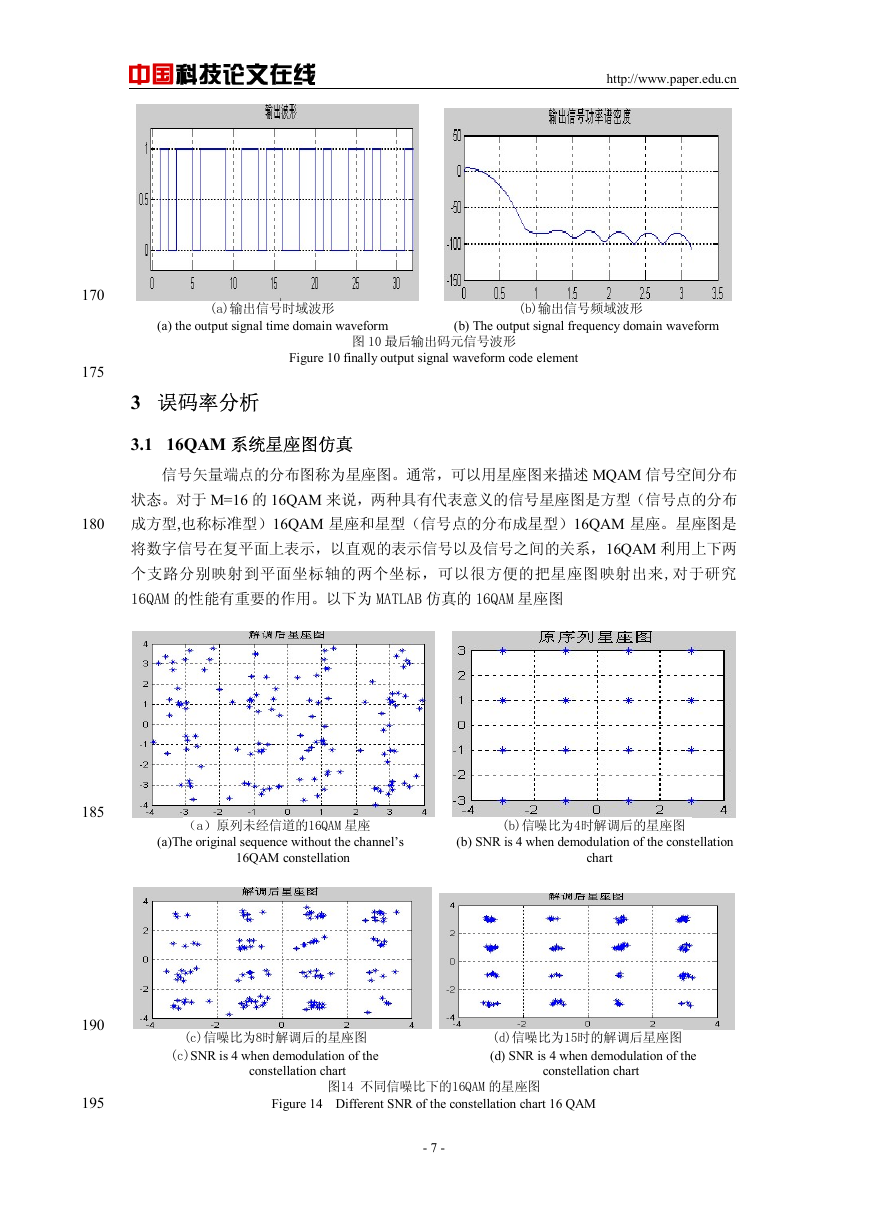通过载波器后形成两路频带信号携带信源信息，其中各个支路的已调信号及其功率谱密度的仿真结果如图 4 所示 (a)上支路已调信号 (b)下支路已调信号 (a)up branch modulated signal (b)down branch modulated signal (c)上支路已调信号频域信号 (d)下支路已调信号频域信号 (c)up branch modulated signal frequency signal (d)down branch modulated signal frequency signal 图 4 各个支路的频带信号 Figure 4 each branch of the band signal 115 两路已调频带信号再经过相加器就形成了 16QAM 调制信号。16QAM 仿真波形如图 5 和图 6 所示（图中为不同时段的 16QAM 信号）: - 4 -

中国科技论文在线 http://www.paper.edu.cn 图 5 16QAM 信号时域波形图 6 16QAM 信号的频域波形 Figure 5 16QAM time domain waveform signal Figure 6 16QAM signal frequency domain waveform 2.2 16QAM 解调系统仿真上节已经仿真出 16QAM 的调制信号，信号经过不同信道的传输发送到接收机上。其中 Awgn 信道的信噪比可以自由适应不同的要求（QAM=awgn(QAM,snr)），这也是 MATLAB 仿真的方便之处。本节中的解调过程不加任何信道，已调信号 16QAM 经过相乘器来完成相干解调，载波信号由载波恢复来提取。相干解调后的仿真波形如图 7 所示 (a)上支路经过相干解调波形 (b)下支路经过相干解调波形 (a)After the coherent demodulation waveform on branch (b)After the coherent demodulation under branch waveform 120 125 130 Figure 7 16 QAM after the coherent demodulation multiply the waveform 图 7 16QAM 经过相乘器相干解调波形经过相干解调产生频带和基带信号，下一步设计滤波器滤掉高频信号产生基带信号，进 135 一步还原原始信号。其中低通滤波器的设计如下： %低通滤波器的设计 b=fir1(32,0.2);I3=filter(b,1,I2)*2; Q3=filter(b,1,Q2)*2; 低通滤波器的延时为 1，信号经过低通滤波器产生的信号如图 8 所示 (a)经低通滤波器后上 I 支路的信号 (b)经低通滤波器后 Q 上支路的信号 (a) The low pass filter on the signal after I branch (b) the low-pass filter on the signal after Q branch 图 8 信号经低通滤波后的信号波形 Figure 8 signal by low pass filtering signal waveform - 5 - 140 145

中国科技论文在线 http://www.paper.edu.cn 由于此时形成的信号波形是模糊不平滑，再设计多电平判决器对信号进行处理得到规则的波形，由于四进制信号的幅度分别为-3 -1 1 3，那么根据最佳码元判决规则，决定判据的门限电压为 0.5，转换为数学公式为： 3a + < 1a <+ 1a <− 3a − < 3 −=⋅⋅ 1 −=⋅⋅ 1 +=⋅⋅ 3 +=⋅⋅ 0.5 0.5 0.5 0.5 b b b b ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ (2) 150 经过多电平判决可产生信号波形，如图 9 所示图 9 经多电平判决后的波形 Figure 9 The multilevel post-sentence waveform 155 4-2 电平转换：由于调制系统中的 2-4 电平转换采用格雷码编码，在解调中同样要用格雷码反编码，并且码元速率增倍，具体的形式如下式： ]00[3 =− ]01[1 =− ]11[1 =+ ]01[3 =+ ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ 根据式(2)、（3）基于 MATLAB 的算法应设计为： k=1; （3） 160 for i=1:N/4;j=1+4*i-4; if abs(I3(1,1000*j)+3)<1;I4(1,k:k+1)=[0 0]; elseif abs(I3(1,1000*j)+1)<1;I4(1,k:k+1)=[0 1]; elseif abs(I3(1,1000*j)-1)<1;I4(1,k:k+1)=[1 1]; elseif abs(I3(1,1000*j)-3)<1;I4(1,k:k+1)=[1 0]; 165 end k=k+2; End 最后形成的两路已解调完成的信号经过并串变换，输出二进制波，解调完成。此时的码元速率应为进入解调器上下两路信号的 4 倍。最后输出序列仿真波形如图 10 所示 - 6 -

中国科技论文在线 http://www.paper.edu.cn (a)输出信号时域波形 (b)输出信号频域波形 (a) the output signal time domain waveform (b) The output signal frequency domain waveform 图 10 最后输出码元信号波形 Figure 10 finally output signal waveform code element 3 误码率分析 3.1 16QAM 系统星座图仿真信号矢量端点的分布图称为星座图。通常，可以用星座图来描述 MQAM 信号空间分布状态。对于 M=16 的 16QAM 来说，两种具有代表意义的信号星座图是方型（信号点的分布成方型,也称标准型）16QAM 星座和星型（信号点的分布成星型）16QAM 星座。星座图是将数字信号在复平面上表示，以直观的表示信号以及信号之间的关系，16QAM 利用上下两个支路分别映射到平面坐标轴的两个坐标，可以很方便的把星座图映射出来,对于研究 16QAM 的性能有重要的作用。以下为 MATLAB 仿真的 16QAM 星座图（a）原列未经信道的16QAM 星座 (b)信噪比为4时解调后的星座图 (a)The original sequence without the channel’s (b) SNR is 4 when demodulation of the constellation 16QAM constellation chart (c)信噪比为8时解调后的星座图 (d)信噪比为15时的解调后星座图 (c)SNR is 4 when demodulation of the (d) SNR is 4 when demodulation of the constellation chart constellation chart 图14 不同信噪比下的16QAM 的星座图 Figure 14 Different SNR of the constellation chart 16 QAM - 7 - 170 175 180 185 190 195

中国科技论文在线 http://www.paper.edu.cn 可以看出信噪比越大，还原出的信号星座图越规范，点越集中。说明随信噪比变小星座图的各点距离也相应的变小，信号的差错率也会变小。 3.2 16QAM 的误码率分析误码率主要取决于星座图中信号点之间的最小距离。本节分析方型星座图下信号的误码 200 率。设信号点之间的最小距离为 dmin。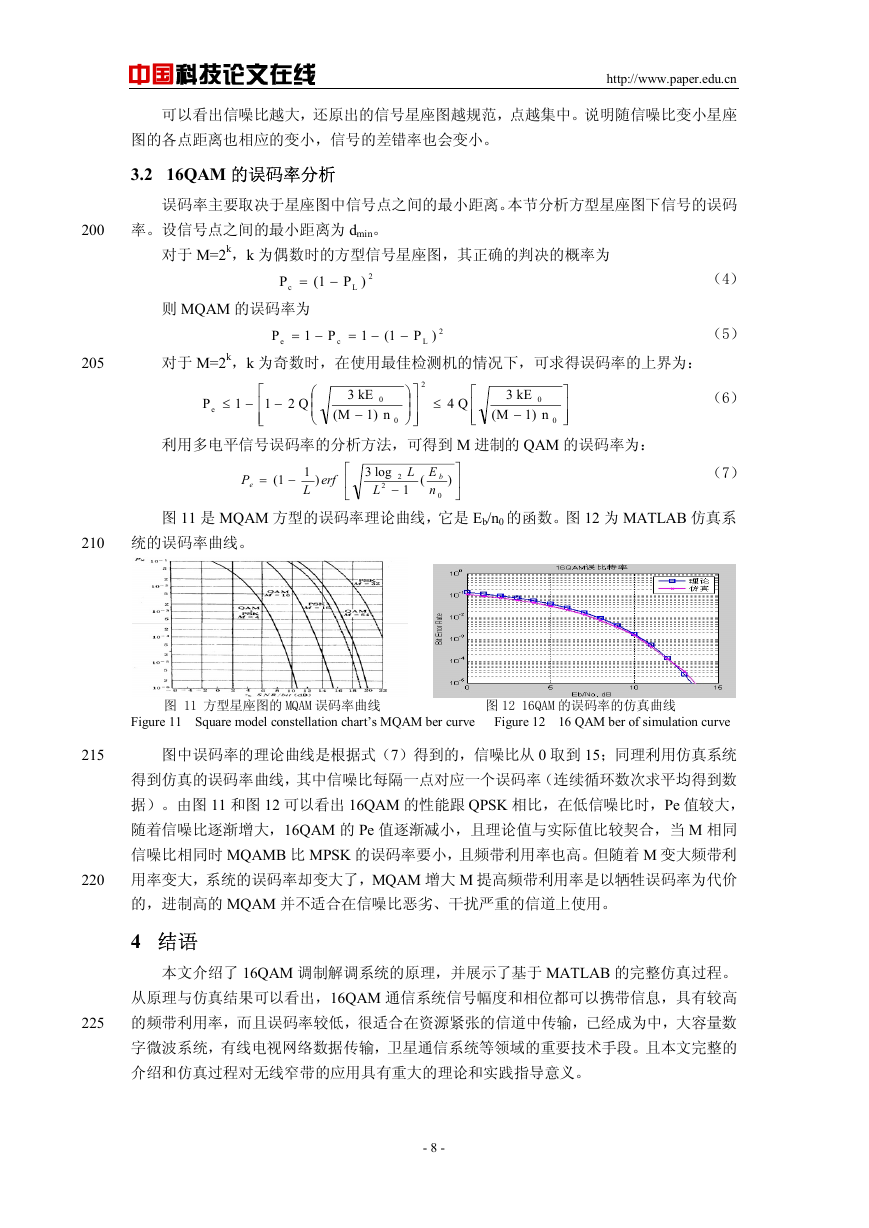 P c (1 对于 M=2k，k 为偶数时的方型信号星座图，其正确的判决的概率为 = 则 MQAM 的误码率为 1 对于 M=2k，k 为奇数时，在使用最佳检测机的情况下，可求得误码率的上界为：（4）（5） )P L −= 1 )P L P e P c (1 − = − − 2 2 205 P e ≤ 1 − ⎡ 1 ⎢ ⎢ ⎣ − Q2 ⎛ ⎜ ⎜ ⎝ kE3 − 0 n1) (M 2 ⎞ ⎟ ⎟ ⎠ ⎤ ⎥ ⎥ ⎦ 0 ≤ Q4 ⎡ ⎢ ⎢ ⎣ kE3 − 0 n1) (M （6） ⎤ ⎥ ⎥ ⎦ 0 利用多电平信号误码率的分析方法，可得到 M 进制的 QAM 的误码率为： P e = 1( − )1 L erf ⎡ ⎢ ⎣ 3 log L 2 2 − L 1 ( E n b 0 ) ⎤ ⎥ ⎦ （7）图 11 是 MQAM 方型的误码率理论曲线，它是 Eb/n0 的函数。图 12 为 MATLAB 仿真系 210 统的误码率曲线。 215 220 225 图 11 方型星座图的 MQAM 误码率曲线图 12 16QAM 的误码率的仿真曲线 Figure 11 Square model constellation chart’s MQAM ber curve Figure 12 16 QAM ber of simulation curve 图中误码率的理论曲线是根据式（7）得到的，信噪比从 0 取到 15；同理利用仿真系统得到仿真的误码率曲线，其中信噪比每隔一点对应一个误码率（连续循环数次求平均得到数据）。由图 11 和图 12 可以看出 16QAM 的性能跟 QPSK 相比，在低信噪比时，Pe 值较大，随着信噪比逐渐增大，16QAM 的 Pe 值逐渐减小，且理论值与实际值比较契合，当 M 相同信噪比相同时 MQAMB 比 MPSK 的误码率要小，且频带利用率也高。但随着 M 变大频带利用率变大，系统的误码率却变大了，MQAM 增大 M 提高频带利用率是以牺牲误码率为代价的，进制高的 MQAM 并不适合在信噪比恶劣、干扰严重的信道上使用。 4 结语本文介绍了 16QAM 调制解调系统的原理，并展示了基于 MATLAB 的完整仿真过程。从原理与仿真结果可以看出，16QAM 通信系统信号幅度和相位都可以携带信息，具有较高的频带利用率，而且误码率较低，很适合在资源紧张的信道中传输，已经成为中，大容量数字微波系统，有线电视网络数据传输，卫星通信系统等领域的重要技术手段。且本文完整的介绍和仿真过程对无线窄带的应用具有重大的理论和实践指导意义。 - 8 -

资料库

论文研究-16QAM调制解调技术分析与MATLAB仿真 .pdf

相关推荐

开发技术

热门标签

最新资料