★★世纪期刊网-专业论文文献原文传递服务网站★★ 【关于我们】 世纪期刊网专业提供中文期刊及学术论文、会议论文的原文传递及下载服务。 【版权申明】 世纪期刊网提供的电子版文件版权均归属原版权所有人，世纪期刊网不承担版权问题，仅供您个人参考。 【意见建议】 请您不要丝毫保留对我们网站发展的意见建议，对于提出意见建议的朋友我们将提供单独的账户。 【联系方式】 商务及服务电话 013328196150 在线QQ 3042329 电子邮件 support@verylib.com 【访问网站】 世纪期刊网 http://www.verylib.com 【网上购书】 当当网(图书最多) 卓越亚马逊网(送货最快) 华储网(专业计算机图书） 99读书人网(新秀推荐) 【网上商城】 京东商城(推荐商家) 【网上购物】 淘宝网 ★★百万篇博硕本科论文全新推出★★ 网址http://www.verylib.com.cn/ 本次文章生成时间：2009-5-6 21:55:30 文章内容从第二页开始！ 请将本站向您的朋友传递及介绍！ 

第20卷 第8期 工 程 数 学 学 报 v。1．20 N。．8 。。 年 月 JOURNAL OF ENGINEERING MATHEMATICS Dec． 00 文章编号 ：1005—3085 (2003)08—0053—04 水塔水流量的估计建模 戴永红 ， 赫孝 良， 李继成 (西安交通大学理学院 ，西安 710049) 摘 要 ：数学建模实验是近几年才 出现的一门新课程 ，全国有许多高等院校已先后开设了该课程 ，这方 面的教学工作 尚处在探索阶段 ，本文通过一个具体的教学课件介绍 了我们在这方面的一些尝试。 关键词 ：数学建模实验 ，数据插值 分类号 ：AMS (2000)97D50 中图分类号：TBll5 文献标识码 ：A 数学建模实验课的 目的在于使学生学会借助于飞速发展的计算机技术和一些数学软 件，利用一种或者多种数学方法解决一些实际问题。学生通过实际问题的要求，建立简单 的数学模型 ，经过简单的软件编程、上机操作、完成实验任务等学习过程 ，真正体会到数 学的奥妙，做到学数学，用数学 ，从而激发学生学习数学的兴趣。数学实验课程的开设在 国内尚处在探索阶段，下面我们 以一个具体的教学课件为例介绍我们在这方面的一些尝 试。我们的总体思想是以实际问题为线索，如要用到新的知识点，只介绍基本原理和方 法，强调 ‘会用’，在解决问题时，尽可能用不同的方法，以提高学生对知识的应用兴趣 和解决实际 问题 的动手能力 。 l 实验问题 ：水塔水流量的估计 此问题 为选 自 MCM91A题 美国一个用水管理机构要求各社区提供以每小时多少加仑计的用水率以及每天所用的 总水量。许多社区没有测量流人或流出水塔的水量装置，他们只能代之以每小时测量水塔 中的水位，其误差不超过 5％。当水塔中的水位下降到最低水位 L时水泵就启动向水塔输 水直到最高水位 H，期间不能测量水泵的供水量。因此 ，当水泵正在输水时不容易建立水 塔中水位和用水量之间的关系。水泵每天输水一次或两次 ，每次约二小时。 试估计任何时刻从水塔流出的水流量 f(t)，并估计一天的总用水量。已知该水塔是 一 个高为 40英尺 (ft)，直径为 57英尺 (ft)的正圆柱，表 1给出了某个小镇一天水塔水 位的真实数据 ，水位降至约 27．OOft水泵开始工作，水位升到 35．5Oft停止工作。 收稿 日期：2003．1l-15． 作者简介 ：戴永红 (1969年生)，男 ，硕士 ，讲师 

54 工 程 数 学 学 报 第 20卷 表 1 某 小镇 某天水 塔水 位 时 间／s 水位 ／0．01ft 时 间／s 水位 ／0．01ft 0 3316 6635 10619 13937 17921 21240 25223 28543 32284 35932 39332 39435 43318 3175 3110 3054 2994 2947 2892 2850 2795 2752 2697 水泵 开动 水泵 开动 3550 3445 46636 49953 53936 57254 60574 64554 68535 71854 75021 79254 82649 85968 89953 93270 3350 3260 3167 3087 3012 2927 2842 2767 2697 水 泵开动 水 泵 开动 3475 3397 3340 2 问题分析 流量是单位时间内流出水的体积，由于水塔是正圆柱形，横截面积是常数 ，所以在水 泵不工作时段 ，流量很容易根据水位相对时间的变化率算出。问题的难点在于如何估计水 泵供水 时段 的流量 。 水泵供水时段的流量只能靠供水时段前后的流量经插值或拟合得到。这些流量大体上 可由两种方法计算，一是直接对表 1中的水量用数值微分算出各时段的流量，用它们拟合 其它时刻或连续时间的流量 ；二是先用表中数据拟合水位 一时间函数 ，求导数即可得到连 续时间的流量 。 有了任何时刻的流量 ，就不难计算一天的总用水量。其实 ，水泵不工作时段的用水量 可以由测量记录直接得到 ，由表 1中下降水位乘以水塔的截面积就是这一时段的用水量。 这个数值可以用来检验数据插值或拟合的结果。 通过上述的分析，在具体给出本问题的解答之前，有必要先介绍一些有关数值微分， 数据插值及数据拟合的基本理论和方法 ，不必进行严格的理论推导 ，强调 ‘会用 ’。 3 问题求解 为了表示方便 ，我们将问题中所给表 1中的数据全部化为国际标准单位，时间用小时 (h)，高度用米 (m)(具体数据这里略去)。 模型假设 1)流量只取决于水位差 ，与水位本身无关，故由物理学中Torricelli定律： 从小孔流出的液体的流速正比于水面高度的平方根。题 目给出水塔的最低和最高水位分别 是 8．1648 m 和 10．7352 m (设 出 口的水 位为零 )，因为 sqrt(10．7352／8．1648)≈1． 1467，约为 1，所以可忽略水位对流速的影响。2)将流量看作是时间的连续函数，为计算 简单，不妨将流量定义成单位时间流出水的高度，即水位对时间变化率的绝对值 (水位是 下降的)，水塔截面积为 S．得到结果后乘以 S即可。 流量估计方法 首先将转化为国际标准单位的数据 ，用 MATLAB可以作出时间 一水 位散点图。下面我们来计算水箱流量与时间的关系。一种简单的处理方法是先将这些数据 分为 三段 ，然后对每一段 的数据 做如下处 理 ：设某 段数 据为 {(oZ"o， o)，( 1， 1)，… ，( ， 

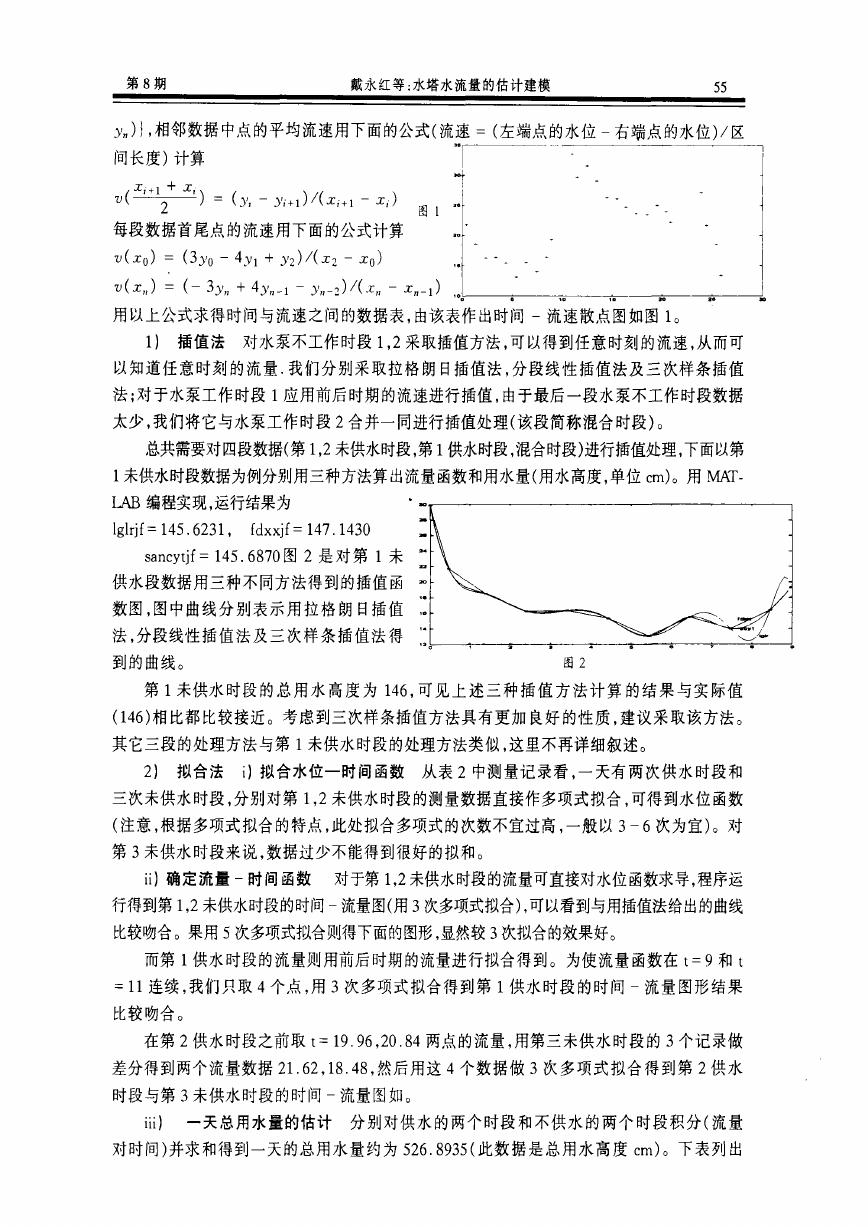
第 8期 戴永红等 ：水塔水流量的估计建模 55 )}，相邻数据中点的平均流速用下面的公式(流速 =(左端点的水位 一右端点的水位)／区 用以上公式求得时间与流速之间的数据表，由该表作出时间 一流速散点图如图 1。 1) 插值 法 对水泵不工作 时段 1，2采取插值方法 ，可 以得到任 意时刻 的流速 ，从而可 以知道任意时刻的流量．我们分别采取拉格朗 日插值法 ，分段线性插值法及三次样条插值 法 ；对于水泵 工作时段 1应 用前后时期 的流速进行插值 ，由于最后一 段水泵不工作 时段数据 太少 ，我们将它与水泵工作时段 2合并一同进行插值处理(该段简称混合时段)。 总共需要对四段数据(第 1，2未供水时段，第 1供水时段，混合时段)进行插值处理，下面以第 1未供水时段数据为例分别用三种方法算出流量函数和用水量(用水高度，单位 cm)。用 MAT— L 编程实现 ，运行结果为 。 lglrjf=145．6231． fdxxjf=147．1430 sancytjf=145．6870图 2是对 第 1未 供水段 数据 用三种 不同方法得 到的插值 函 数 图 ，图 中曲线分 别 表示 用 拉格 朗 日插值 法 ，分段线性 插值 法及 三 次样 条 插值 法 得 到 的曲线 。 第 1未供水时段的总用水高度为 146，可见上述三种插值方法计算 的结果与实际值 (146)相比都比较接近。考虑到三次样条插值方法具有更加 良好的性质 ，建议采取该方法。 其它三段的处理方法与第 1未供水时段的处理方法类似，这里不再详细叙述。 2) 拟合法 i)拟合水位一时间函数 从表 2中测量记录看，一天有两次供水时段和 三次未供水时段，分别对第 1，2未供水时段的测量数据直接作多项式拟合 ，可得到水位函数 (注意 ，根据多项式拟合的特点，此处拟合多项式的次数不宜过高 ，一般以 3—6次为宜)。对 第 3未供水时段来说 ，数据过少不能得到很好的拟和。 ii)确定流量 一时间函数 对于第 1，2未供水时段的流量可直接对水位函数求导，程序运 行得到第 1，2未供水时段的时间一流量图(用 3次多项式拟合)，可以看到与用插值法给出的曲线 比较吻合。果用 5次多项式拟合则得下面的图形，显然较 3次拟合的效果好。 而第 1供水时段的流量则用前后时期的流量进行拟合得到。为使流量函数在 t=9和 t =l1连续，我们只取 4个点，用 3次多项式拟合得到第 1供水时段的时间 一流量图形结果 比较吻合。 在第 2供水时段之前取 t=19．96，20．84两点的流量，用第三未供水时段的 3个记录做 差分得到两个流量数据 21．62，18．48，然后用这 4个数据做 3次多项式拟合得到第 2供水 时段与第 3未供水时段的时间 一流量图如。 iii) 一天总用水量的估计 分别对供水的两个时段和不供水 的两个 时段积分(流量 对时间)并求和得到一天的总用水量约为 526．8935(此数据是总用水高度 cm)。下表列出 

56 工 程 数 学 学 报 第 20卷 各段用水量数值。 表 2 时 段 l第1未供水段 l第2未供水段 l第1供水段 I第2供水段 l全天用水 用水高度 1 145．67 I 260．66 l 46．60 I 73．9635 l 526．893 i )流量及总用水量的检验 计算出各时刻的流量可用水位记录的数值微分来检验，各时 段的用水高度可以用实际记 录的水位下降高度来检验。例如 ，算得第 1未供水段 的用水量高度 是 145．67cm，而实际记录的水位下降高度为 146cm，两者是吻合的；同样地，算得第 2未供 水段的用水量高度是 260．66cm，而实际记录的水位下降高度为 260cm，两者也是吻合的。 从算法设计和分析可知，计算结果与各时段所用的拟合多项式的次数有关。下表给出 的是对第 1，2未供水时段分别用 5、6次多项式拟合后得到的用水量结果。 表 3 时 段 I第1未供水段 l第2未供水段 I第1供水段 I第2供水段 l全天用水 用水高度 l 146．5150 I 257．7605 i 46．1317 l 76．3076 I 526．7148 结果分析 对方法 1)，可以看 出，使用三次样条插值法得到的结果 (145．6870， 258．6547)与原始记录的下降高度 146，260相差不大，说明插值结果与原始数据比较吻 合。按三次样条插值法估计出全天的用水高度约为 539．4450 cm；对方法 2)，由表 3可 以得 到全 天的用水高度 约为 526．7148 cm，两种方 法得 到 的数据 比较接 近 ，也说 明两 种 方法在解 决该实际 问题 时都是可行 的。 4 内容小结 本实验主要进行水塔水流量的估算建模。第一种估算方法为插值方法 ，我们用了三种 不同的插值法进行估计 。在求解的过程中，可以熟悉数据插值的理论和方法；第二种估算 方法为数据拟合法 ，用多项式进行拟合 ，得到水塔水流量的估计。通过该实验，使学生能 够处理 这类有着不 完全数据的实 际问题 ，提高学 生解决实 际问题的能力 。 参 考文献 ： [1] 叶其孝 ．数学建模教育与国际数学建模竞赛 [J]．工科数学专辑 ，第 10卷 ，65—70(总第 50期) [2] 萧树铁 ．数学实验 [M]．北京 ：高等教育出版社 ，1999 [3] 周义仓 ，赫孝 良．数学建模实验 [M]．西安：西安交通大学出版社 ，1999 Estimating the W ater Flux of the W ater Tower DAI Yong—hong， HE Xiao—liang， LI ji—cheng (Xi’3n Jiaotong University，Xi’3n 710049) Abstract：M athematical modeling Experiments is 3 new course，and developped in many universities in recent years， the teaching about this course is exploring phasee at present， in this paper，we introduce our experiment in teaching about this course by 3 specific teaching example． Keywords：mathematical mod eling；data intenpolation