比例导引规律的指令加速度.pdf-资料库

性洲刹〕年第期总第期电光与控制比例导引规律的指令加速度雷虎民西北工业大学西安印刘兴堂空军导弹学院西安陈新海西北工业大学西安摘要根据指令加速度的不同参考作用方向 , 形成和定义不同形成的比例导引制导规律。这些规律主要分为三类一类是以追踪速度矢量为参考基准 , 如纯比及其各种变化形式另一类是以追踪与目标之间的视线为参考基准 , 如真比例导引等第三类是以追踪器与目标之间的相对速度为参考、广义比例导引例导引基准 , 如理想比例导引正等。本文概述了这些制导规律的研究现状 , 建立了矢童形式的相对运动方程 , 给出了相应的指令加速度构成 , 讨论了这些制导规律应用在战术导弹上的适用性 , 比较了这些制导规律的有关性能。关键词战术导弹制导规律指令加速度数学模型比例导引引言是应用于战术导弹的一种有效的寻的制导规律。经过几十年来的发展和创新 , 这种制导规律已经从原始的定义更新了许多 , 出现了各种各亲戚的变化形式。仅按照指令加速度的不同作用方向应形成和定义了多种以追踪速度矢量为参考基准月、广义比例导引的有纯比例导引 , , 等以相对矢量为参考基准的有理想比例导引少。上述几种比例导引的追汇’ 以视线为参考基准的有真比例导引比例导引 ’, 踪几何如图所示。这些研究的主要特点是以视线或相对速度为参考基准的制导规律在数学分析时是较易处理的 , 对于非机动或特定机动目标存在精确的闭合形式解 , 虽然这些解的大多数情况仍然是隐含的 , 即解的形式以为自变量而不是以为自变量。但是 , 相对于以追踪器速度方向为参考基准的只能进行定性的数学分析相比 , 这种分析上的优越性仍然是可贵的。这也许就是众多研究者都在研究前者且出现大量文献的原因吧然而 , 上述这些规律在数学分析时的易处理性并不等于实际应用时的易实现性。事实上 , 这些规律很少讨论实际工程中如何应用 , 对追踪器也作了许多简化假设 , 甚至认为是一个理想飞行体。本文将重点以工程应用为背景来讨论这些规律的应用价值 , 不同参考基准对指令加收稿日期塑一的一修回日期卯一一

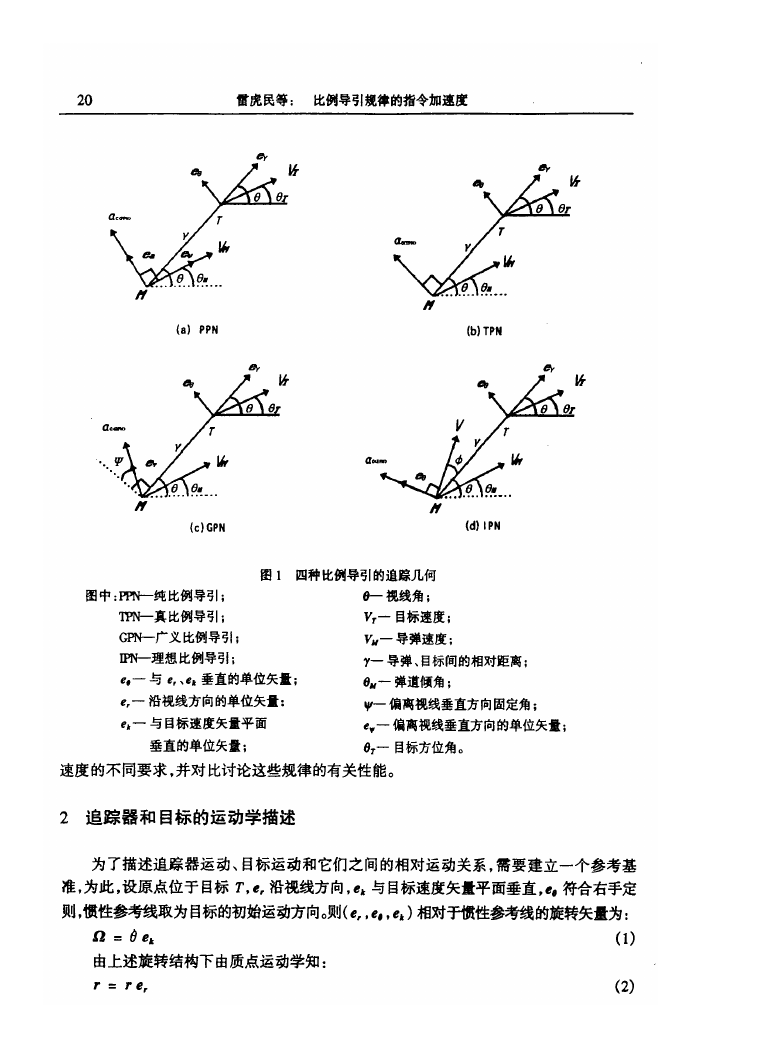
雷虎民等比例导引规律的指令加速度创图四种比例导引的追踪几何图中巧州‘一纯比例导引一真比例导引一广义比例导引任刊一理想比例导引 ’一与、。垂直的单位矢。一沿视线方向的单位矢 ‘ 一与目标速度矢盘平面垂直的单位矢盘口视线角一目标速度玲一导弹速度一导弹、目标间的相对距离 ‘ 一弹道倾角甲一偏离视线垂直方向固定角 ‘ 一偏离视线垂直方向的单位矢盘氏一目标方位角。速度的不同要求 , 并对比讨论这些规律的有关性能。追踪器和目标的运动学描述为了描述追踪器运动、目标运动和它们之间的相对运动关系 , 需要建立一个参考基 , 沿视线方向 , 。, 与目标速度矢平面垂直 , 符合右手定准 , 为此 , 设原点位于目标 , 则 , 惯性参考线取为目标的初始运动方向。则。, 口二夕口由上述旋转结构下由质点运动学知二口 , 。。 , 相对于惯性参考线的旋转矢量为、户、,矛百且,山矛百、了‘、

燮为年第期总第期电光与控制二 ‘ , 矽。 , , 厂一矽形矽。。追踪器和目标的速度矢量可分别分解为嵘一。一玲二口一口一一夕一。。设追踪器相对目标的相对速度矢量为从巧。 , 矽。相对速度矢量与蛛和的关系为一「一一一、〕, 「一一口一」。则相对速度分量关系为叭 ‘ 一夕一喃巧矽一玲一琉一一设追踪器和目标加速度分别为和 , 把他们沿视线方向和视线垂直方向。分解 , 并且把按照形式可表示为口材二户二口口刃肠由基本运动学关系 , 我们有相对运动方程为一 , 因此 , 相对运动方程的分量表达式为 , 一矽一八户刁十矽气一刀按照指令加速度不同作用方向定义的各种比例导引规律实质上对应于比例系数和。的不同组成参量 , 由于这种组成参量的不同使得这些制导规律具有各自不同的特点和要求。下面来考察、、、这四种规律的指令加速度要求及分析特点。指令加速度的构成与实现纯比例导引在设 , 为追踪器速度方向的单位矢量 , 中 , 指令加速度作用在追踪器速度的垂直方向 , 幅值与视线角速率成正比。定义的指。为速度垂直方向的单位矢量 , 根据令加速度为 , 凡刀。在对追踪器与目标之间的相对运动学关系进行分析时 , 通常是按视线方向和视线垂直方向来分析的 , 因此需要把指令加速度沿和。方向分解得

雷虎民等比例导引规律的指令加速度哪因此 , 刃叭刀。夕一。一八。刀啼一、 , 八。。。」刀啼一 , , 由和。的关系式可知 , 求解这种规律的精确的闭合形式解是很困难的 , 一。空间追踪器的控制通常是按照追踪器速度方向和速度垂直方向来实施的 , 因此在对规律正好只需对速度追踪器进行控制计算时必须把指令加速度沿这两个方向分解。垂直方向进行控制。真比例导引在幅值与视线角速度和接近速度的乘积成正比时 , 称为实际的真比例导引中 , 指令加速度作用在视线的垂直方向 , 而幅值仅与视线角速率成正比。当。由于更具有普遍意义 , 我们就以这种定义为基础进行讨论。一一甲。因此 , , 。一认可以看到 , 由于比例系数 , 和。具有简单的变量组成形式 , 因而对于非机动目标或特殊的机动目标形式经过简单推导即可得到精确的闭合形式解。把指令加速度沿。和 , 方向分解得二二一姗「因此 , 为了实现 , 一口, 。一、 , 〕 , 需要对这两个方向都进行控制。广义比例导引在位矢量为如 , 其幅值也与视线角速率成正比。而在实际的广义比例导引中 , 指令加速度作用在偏离视线垂直方向固定角少的方向 , 设这个方向的单中 , 指令加速度幅值与视线角速率和接近速度的乘积成正比。由于这种规律为基础进行讨论。更具一般性 , 本文就以。。一动如一刃夕肠。二一认乡。宇一肠。伞一因此 , , 一口少 , 。二一助伞制。寻的导弹这种比例系数也存在一定的闭合解。为了实现 , 需要对这两个方向都进行控制导的基本概念就是尽快地用控制指令把导弹的前置角转到某一期望的方向 , 而控制指令与这个方向的旋转角速率成正比。因此 , 需要寻找偏置角伞的最优值。理想比例导引在理中 , 指令加速度作用在相对速度的垂直方向 , 幅值和视线角速率与相对速度的乘积成正比。设相对速度垂直方向的单位矢量为即 , 根据正定义的指令加速度为 , , 刃帕‘ 一刀认白。一刃动

癸年第期总第期电光与控制帕。价 , 。 , 二一一 , 必一从丫衅此 , 笋巧认因此 , 式中 , 根据指令加速度组在参量的简单性 , 使得护对于非机动或特殊的机动目标存在准确的闭合形式解。为了实现这种规律 , 也需要对速度方向及其垂直方向施加控制。上面我们分别介绍了四种制导规律的定义 , 指令加速度组成及关于分析的控制的矢量分解。由于后三种规律对应比例系数 , 和。组成参量的特、和、、、等都有准确的解析表达式。根据这殊性 , 使得他们都有准确的闭合形式解 , 即口、矛、些解析解 , 可以方便地分析这些制导规律的有关性能。而且由于指令加速度同时从两个方向作用 , 因此 , 具有较高的制导精度。但是由于的比例系数具有完全不同的结构 , 因此没有精确的团合解 , 并且因为这种区别使得上面三种规律成熟的分析方法并不能应中。另一方面 , 后三种规律却需要从两上方向对追踪器施加控制。为了实现这用在些制导规律 , 追踪器必须相应提供这些指令加速度 , 也就是说追踪器必须提供速度方向一速度垂直方向的机动加速度。然而 , 对于飞行在大气层内由空气动力控制机动运动的战术导弹 , 作用在导弹速度方面的外力是不可调节的 , 而自动驾驶仪舵机可以根据控制指令要求进行适当偏转 , 以产生速度垂直方向动力。这就是说对导弹速度方向不能施加控制 , 而只能对速度的垂直方向进行控制。在这种情况下 , 只有制导规律是可实现的。对于飞行在大气层外的空间拦截器 , 对这两个方向均可实行控制 , 但要以消耗能量为代价。通常对速度方向的控制是保持这个方向的速度恒定 , 因此 , 不论加减速都要消耗能量。这时衡量制导性能优劣的一个重要的性能指标就是追踪器速度增量。因为速度增量是与能量消耗相等价的。数字仿真结果也验证了这种结论的正确性 , 由于篇所限 , 本文没有给出实际系统仿真模型和结果曲线。结论、、本文研究了、和护和指令加速度形成 , 给也了相对运动学环节的数学描述 , 讨论了这些制导规律的应用限制。研究结果表明后三种规律在运动方程的要解性分析中具有一定的优点 , 制导精度较高 , 但这些方案遭受严格的限制。其中主要的缺点有前向速度变化要求 , 即要求使用推动器 , 在靠空气动力控制的追踪器中不可能实现要求较大的效导航比 , 但是 , 由于后三种规律特别是的良性能 , 因此有望在空间拦截和空间飞行器的交会与对接中得到实际应用。参 ,考文献 , , 男一即记即刀即、邵洲田此 , 哩 , 田巧一以 , 飞、, 助 , 塑〕 , 一

电光与控制望沟年第期总第期一种新型状态观测器在陀螺稳定平台中的应用石红生卢广山中航总第六一三研究所洛阳以摘要对影响陀螺稳定平台精度的主要因素进行了分析 , 指出扰动力矩是其中重要因素之一。并分别用一般观测器和基于神经网络的观测器对系统进行设计。结果表明采用一般状态观测器设计可以在很大程度上提高系统的稳定精度。而基于神经网络的状态观测器设计则更好地提高了系统的稳定精度。关键词陀螺稳定平台状态观测器神经网络算法引言在靶场光电测量设备 , 天文观测设备 , 武器控制系统以及激光通讯系统中 , 都需要有光电捕获跟踪与瞄准装置 , 以便迅速发现并精确跟踪目标 , 在这些系统中 , 都需要对瞄准线田进行稳定 , 因而需要一个固定的空间惯性基准 , 经常由陀螺稳定平台来提供这一基准。对于陀螺稳定平台来说 , 其关键指标之一就是稳定精度 , 影响稳定精度的因素有传感器精度 , 系统动态特性 , 扰动力矩 , 载机振动等 , 其中以摩擦力矩为主的扰动力矩是主要的影响因素。因此 , 如何消除或减小扰动力矩对系统的影响是此类系统设计的核心问题之一。实践证明 , 扰动力矩观测器是一种很好的设计方法。其思想是在线观测出系统的扰动力矩 , 根据不变性原理 , 对其进行动态补偿。陀螺稳定平台的一般模型与分析陀螺稳定平台在其发展过程中 , 出现了许多不同类型的应用。但是它们的基本工作 , , , 一罗 , 犯巧卯 , ’ 』 , 拍男 , 一骊五 , 吻汕〕即 , 一汕喇出咫 ,柏托时而即伍庄 , , 伪 , 一卜五 , 卿 , 巧 , , 一收稿日期为一的一

word版下载：http://www.ixueshu.com ------------------------------------------------------------------------------- 阅读此文的还阅读了： 1. 模糊扩展比例导引研究 2. 基于模糊逻辑的导弹扩展比例导引律 3. 加速度相同的连接体作用规律浅析 4. 带落角约束的圆弧比例导引律和偏置比例导引律的研究 5. 偏置比例导引末制导控制 6. 遗传规律中的特殊比例 7. 指令制导地空导弹的导引规律 8. 具有定常加速度的导弹导引规律 9. 飞行器比例导引综述 10. 广义比例导引规律的准最佳化 11. 依赖于相对距离的最优比例导引规律 12. 基于比例导引的深空撞击脉冲导引律设计 13. 基于比例-最优的组合导引研究 14. 最优偏置比例导引 15. 地空导弹增量式比例导引弹道仿真研究 16. 比例导引法导引弹道仿真研究 17. FANUC 0i系统比例缩放指令初探 18. 一种变系数比例导引规律 19. 捷联导引头积分比例导引制导精度 20. 基于偏置比例导引的模型研究 21. 增量比例导引规律仿真研究 22. 关于比例导引的讨论 23. 基于光流信息的圆弧偏置比例导引规律 24. 地空导弹增量式比例导引弹道仿真研究 25. 偏置比例导引末制导控制

32. 基于导引原理的比例导引弹道的建立 33. 比例导引规律的指令加速度 34. 微分对策制导规律与改进的比例导引制导视规律性能比较 35. BTT-90导弹比例导引规律研究 36. 一种扩展的比例导引规律及其弹道方程的构建 37. 最优导引规律研究 38. 教育指令应遵循教育规律 39. 基于捷联导引头的比例导引制导律设计 40. 比例导引规律在导弹控制系统设计中的应用 41. 考虑重力补偿的BTT-90导弹比例导引规律研究 42. 寻的导弹的变结构比例导引律 43. FANUC系统比例缩放指令的应用 44. 捷联导引头积分比例导引制导精度 45. 比例导引下的机动目标跟踪 46. 一种引入视线角加速度补偿的比例导引算法 47. 配合滚仰式跟踪平台的偏置+比例复合导引律 48. 重力加速度的变化规律 49. 空间自旋稳定拦截器的数字比例导引 50. 时变最优的增强型比例导引及其脱靶量解析研究

资料库

比例导引规律的指令加速度.pdf

相关推荐

开发技术

热门标签

最新资料