第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
近邻法，k近邻法与剪辑近邻法.doc
模式识别上机实验 5：近邻法与剪辑近邻法
画出近邻法的程序框图，对给定的分别存放在文“riply_trn.mat”
和”riply_tst.mat”中的两类样本训练集 250 个测试集 1000 个，试用近邻
法，k 近邻法与剪辑近邻法, 重复剪辑近邻法给出测试集的分类结果并分别
计算其错误率。
一、 实验步骤
一、最近邻法：
将与测试样本最近邻样本的类别作为决策的结果。对一个C 类别问题，每类有 iN 个样
本,
i
1,2,
，则第i 类 i的判别函数为：
C
( ) min ||
g x
i
k
x
k
x
i
||,
k
1,2,
,
N
i
(1)
因此，最近邻决策规则：
若
则决策
g x
j
( ) min
i
( ),
g x i
i
1,2,
c
(2)
x
j
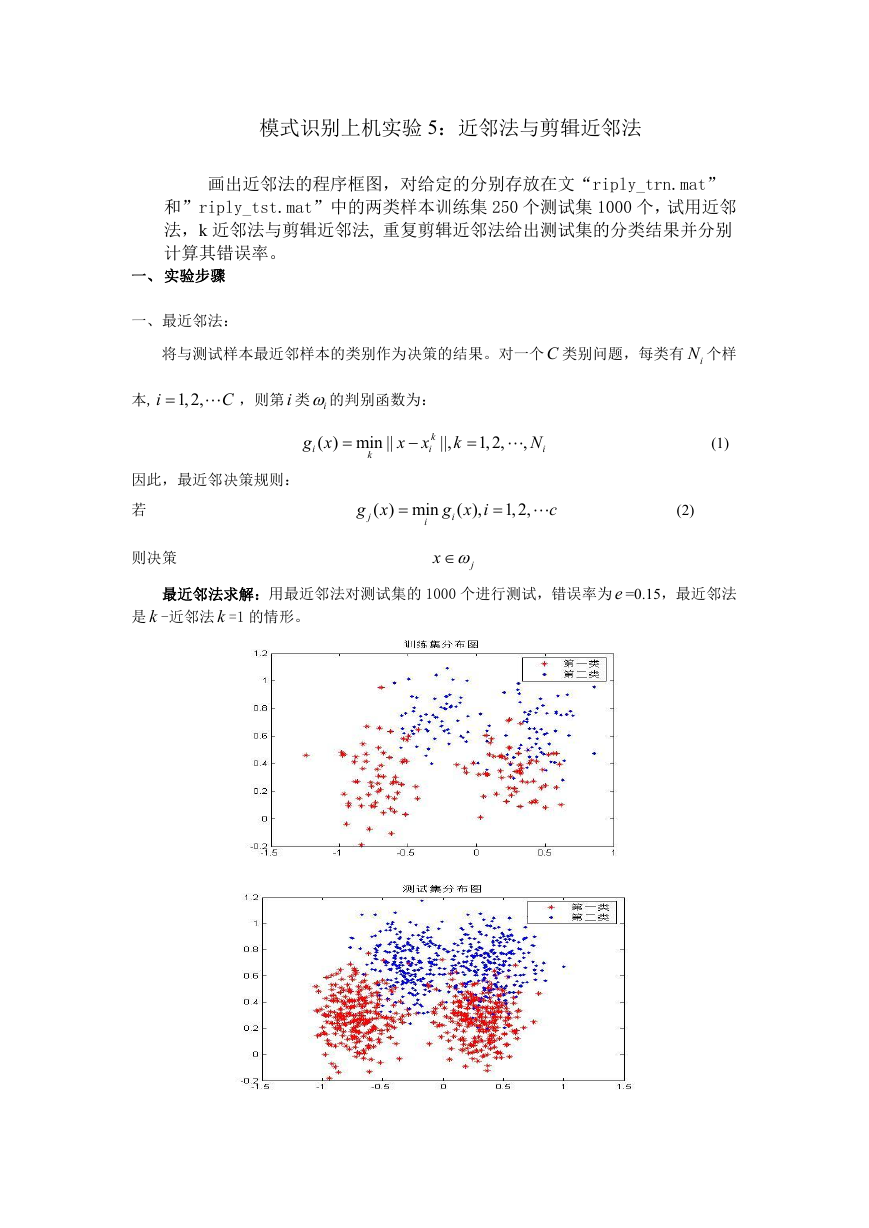
最近邻法求解：用最近邻法对测试集的 1000 个进行测试，错误率为 e =0.15，最近邻法
是 k -近邻法 k =1 的情形。
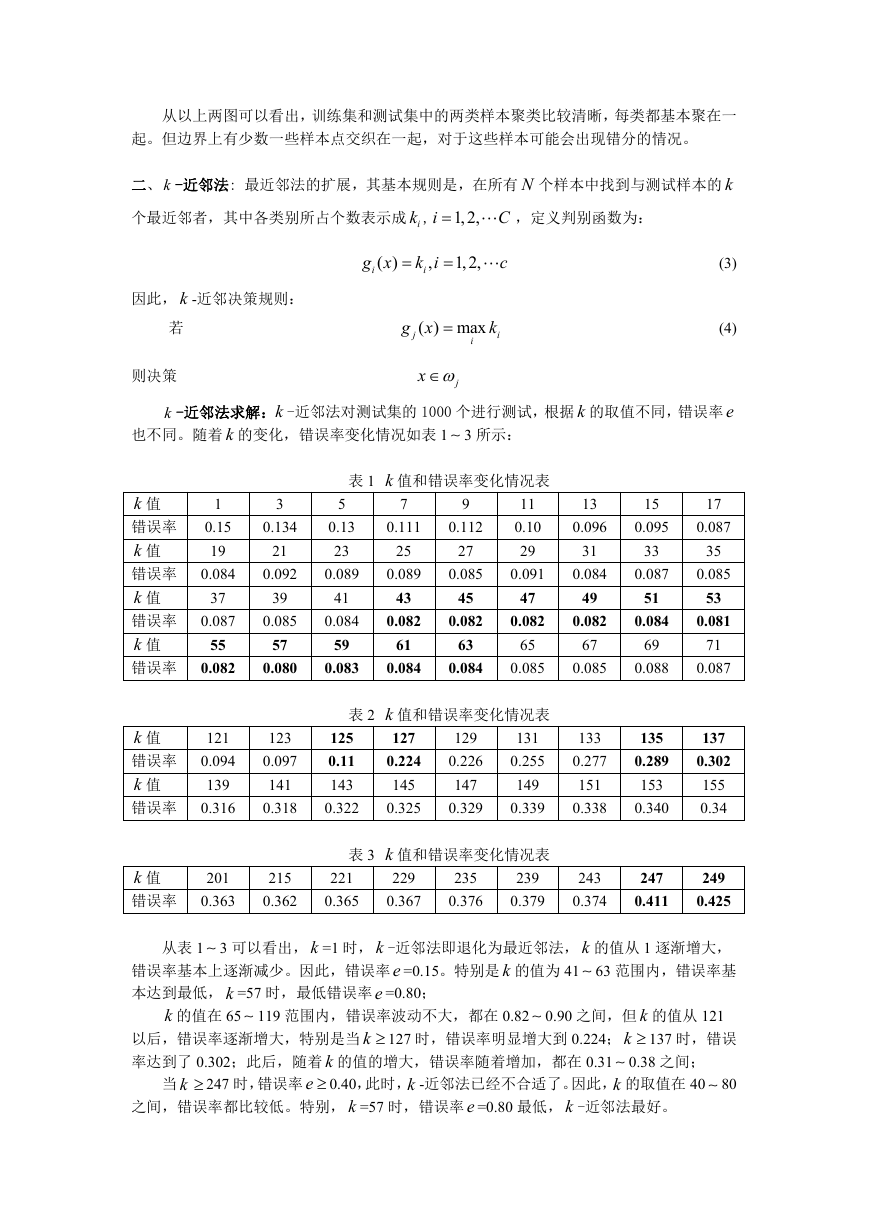
从以上两图可以看出，训练集和测试集中的两类样本聚类比较清晰，每类都基本聚在一
起。但边界上有少数一些样本点交织在一起，对于这些样本可能会出现错分的情况。
二、k -近邻法: 最近邻法的扩展，其基本规则是，在所有 N 个样本中找到与测试样本的 k
个最近邻者，其中各类别所占个数表示成 ik ,
1,2,
，定义判别函数为：
C
i
因此， k -近邻决策规则：
若
则决策
( )
g x
i
,
k i
i
1,2,
c
g x
j
( ) max
i
k
i
x
j
(3)
(4)
k -近邻法求解：k -近邻法对测试集的 1000 个进行测试，根据 k 的取值不同，错误率 e
也不同。随着 k 的变化，错误率变化情况如表 1 3 所示：
k 值
1
错误率 0.15
k 值
19
错误率 0.084
k 值
37
错误率 0.087
k 值
55
错误率 0.082
k 值
121
错误率 0.094
k 值
139
错误率 0.316
3
0.134
21
0.092
39
0.085
57
0.080
123
0.097
141
0.318
k 值
201
错误率 0.363
215
0.362
表 1 k 值和错误率变化情况表
5
0.13
23
0.089
41
0.084
59
0.083
7
0.111
25
0.089
43
0.082
61
0.084
9
0.112
27
0.085
45
0.082
63
0.084
11
0.10
29
0.091
47
0.082
65
0.085
表 2 k 值和错误率变化情况表
131
0.255
149
0.339
127
0.224
145
0.325
129
0.226
147
0.329
125
0.11
143
0.322
表 3 k 值和错误率变化情况表
239
0.379
229
0.367
235
0.376
221
0.365
13
0.096
31
0.084
49
0.082
67
0.085
133
0.277
151
0.338
15
0.095
33
0.087
51
0.084
69
0.088
135
0.289
153
0.340
17
0.087
35
0.085
53
0.081
71
0.087
137
0.302
155
0.34
243
0.374
247
0.411
249
0.425
从表 1 3 可以看出， k =1 时， k -近邻法即退化为最近邻法， k 的值从 1 逐渐增大，
错误率基本上逐渐减少。因此，错误率 e =0.15。特别是 k 的值为 41 63 范围内，错误率基
本达到最低， k =57 时，最低错误率 e =0.80；
k 的值在 65 119 范围内，错误率波动不大，都在 0.82 0.90 之间，但 k 的值从 121
以后，错误率逐渐增大，特别是当 k 127 时，错误率明显增大到 0.224； k 137 时，错误
率达到了 0.302；此后，随着 k 的值的增大，错误率随着增加，都在 0.31 0.38 之间；
当 k 247 时，错误率 e 0.40，此时，k -近邻法已经不合适了。因此，k 的取值在 40 80
之间，错误率都比较低。特别， k =57 时，错误率 e =0.80 最低， k -近邻法最好。
三、剪辑近邻法
对于剪辑近邻法，我们考虑将样本分成两类的情况，则有最近邻剪辑和 k -近邻剪辑法。
3.1 最近邻剪辑：将样本集 N 分成两个互相独立的子集：设计集 NT 和参考集 NR 。
第一步：用参考集 NR 中每一个样本 iy 对设计集 NT 中的样本 ix 用近邻法进行分类。如果
iy 与 ix 不属于同一类别，则将 ix 从设计集 NT 中删除，最后得到一个剪辑的样本集 NTE （剪
辑样本集），以取代原样本集，对待识别样本进行分类；第二步：用剪辑的样本集 NTE 并
用最近邻法对未知的样本 x 进行分类。
最近邻剪辑求解：最近邻剪辑法对测试集的 1000 个进行测试，根据随机分子集的概率
不同，错误率 e 也不同，错误率变化情况如表 4 所示。 1p 表示样本在设计集中的概率， 2p
表示样本在参考集中的概率，(错误率 e 是 20 次错误率的平均错误率，即
e
20
)。
e
i
i
1
1p =0.1
1p =0.2
表 4 最近邻剪辑分类错误率变化情况
1p =0.3
1p =0.4
1p =0.5
1p =0.6
1p =0.7
1p =0.8
2p =0.9
2p =0.8
2p =0.7
2p =0.6
2p =0.5
2p =0.4
2p =0.3
2p =0.2
1p =
0.9
2p =
0.1
0.129
随
机
概
率
错
误
率
0.133
0.136
0.124
0.134
0.130
0.134
0.129
0.136
0.129
0.139
0.134
0.136
0.135
0.141
0.124
0.145
0.149
从表 4 可以看出， 1p 的值从 0.1 逐渐增大到 0.9，设计集中样本个数越来越多，相反，
参考集中的样本数则越来越少。从理论上讲，随着 1p 的增大，错误率也会增大，因为参考
集中的样本个数减少了，参考集决定设计集中的样本是否要剪掉，参考集的可信赖度关系着
p
分类的结果。 1
0.3,
p
2
时，设计集剪辑留下的样本分布如图 3 所示。
0.7
表中错误率有波动，因为设计集和参考集是随机分开的，每次剪辑的样本要依据参考集
样本的好坏。若参考集得可信赖度不高，则分类的错误率比较大。
p
当参考集中的样本数多于设计集中的样本数(即 1
p
2
)时，从 1p =0.1 增大到 0.5 时分
类结果相对比较准确，错误率较小且相对稳定，波动空间相对小。 1p 从 0.5 增大到 0.9，参
考集中样本数越来越少，分类结果越来越依赖参考集。因此，错误率和波动范围都相对较大。
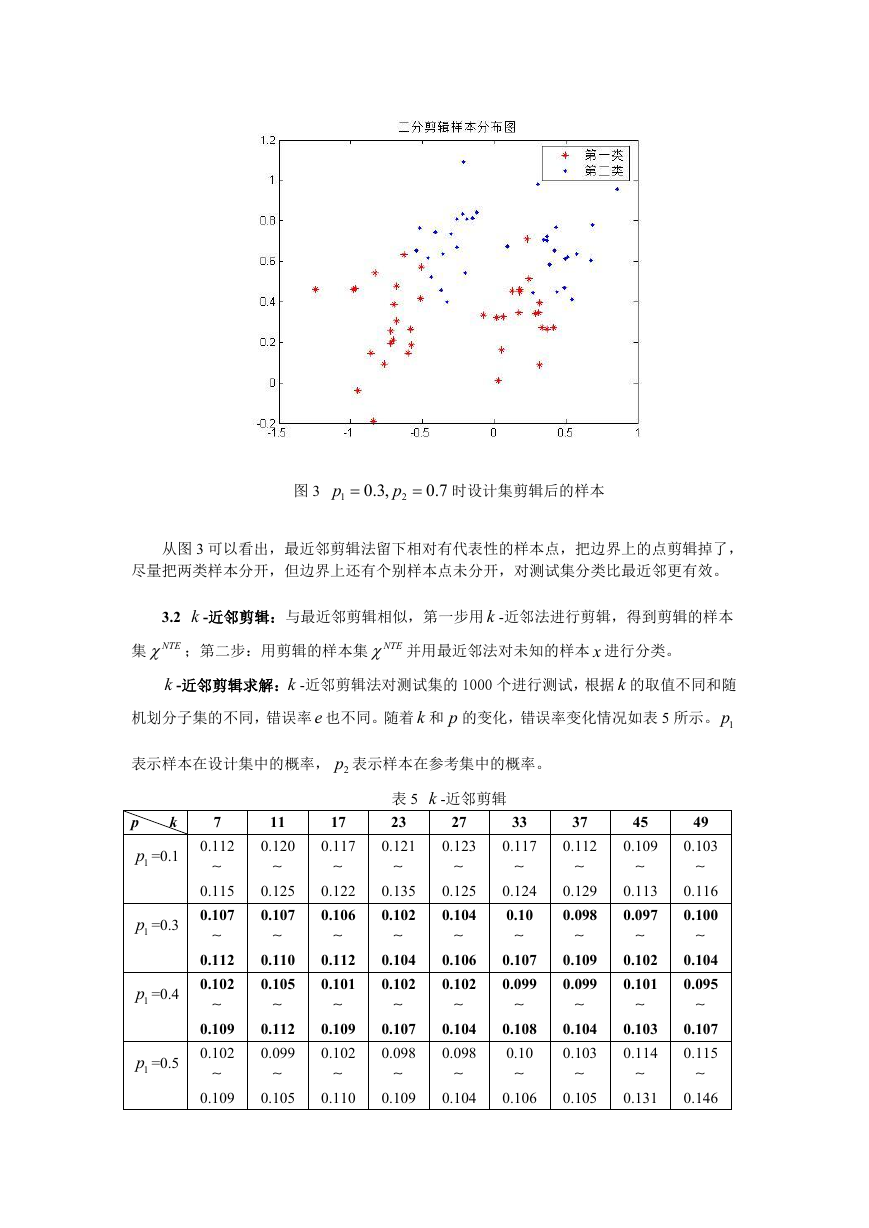
图 3
p
1
0.3,
p
2
时设计集剪辑后的样本
0.7
从图 3 可以看出，最近邻剪辑法留下相对有代表性的样本点，把边界上的点剪辑掉了，
尽量把两类样本分开，但边界上还有个别样本点未分开，对测试集分类比最近邻更有效。
3.2 k -近邻剪辑：与最近邻剪辑相似，第一步用 k -近邻法进行剪辑，得到剪辑的样本
集 NTE ；第二步：用剪辑的样本集 NTE 并用最近邻法对未知的样本 x 进行分类。
k -近邻剪辑求解：k -近邻剪辑法对测试集的 1000 个进行测试，根据 k 的取值不同和随
机划分子集的不同，错误率 e 也不同。随着 k 和 p 的变化，错误率变化情况如表 5 所示。 1p
表示样本在设计集中的概率， 2p 表示样本在参考集中的概率。
p
k
1p =0.1
1p =0.3
1p =0.4
1p =0.5
7
0.112
0.115
0.107
0.112
0.102
0.109
0.102
11
0.120
0.125
0.107
0.110
0.105
0.112
0.099
17
0.117
0.122
0.106
0.112
0.101
0.109
0.102
0.109
0.105
0.110
0.109
0.104
表 5 k -近邻剪辑
23
0.121
27
0.123
0.135
0.102
0.104
0.102
0.107
0.098
0.125
0.104
0.106
0.102
0.104
0.098
33
0.117
0.124
0.10
0.107
0.099
0.108
0.10
0.106
37
0.112
0.129
0.098
0.109
0.099
0.104
0.103
45
0.109
0.113
0.097
0.102
0.101
0.103
0.114
49
0.103
0.116
0.100
0.104
0.095
0.107
0.115
0.105
0.131
0.146
1p =0.6
1p =0.7
p
k
1p =0.1
1p =0.3
1p =0.4
1p =0.5
1p =0.6
1p =0.7
0.103
0.112
0.101
0.111
55
0.123
0.133
0.105
0.106
0.092
0.11
0.135
0.147
0.226
0.268
0.28
0.33
0.103
0.105
0.101
0.106
63
0.106
0.128
0.102
0.107
0.11
0.139
0.171
0.202
0.271
0.348
0.29
0.377
0.101
0.103
0.098
0.112
69
0.114
0.126
0.097
0.106
0.121
0.153
0.231
0.254
0.296
0.310
0.324
0.40
0.097
0.112
0.117
0.126
49
0.103
0.116
0.100
0.104
0.095
0.107
0.115
0.146
0.193
0.243
0.276
0.283
0.099
0.113
0.124
0.138
55
0.123
0.133
0.105
0.106
0.092
0.11
0.135
0.147
0.226
0.268
0.28
0.33
0.193
0.243
0.276
0.283
81
0.117
0.131
0.132
0.156
0.227
0.265
0.275
0.297
0.275
0.348
0.104
0.129
0.153
0.246
63
0.106
0.128
0.102
0.107
0.11
0.139
0.171
0.202
0.271
0.348
0.29
0.377
0.097
0.136
0.191
0.328
69
0.114
0.126
0.097
0.106
0.121
0.153
0.231
0.254
0.296
0.310
0.324
0.40
0.152
0.187
0.284
0.295
75
0.112
0.125
0.107
0.119
0.157
0.203
0.305
0.359
0.288
0.381
0.402
0.442
从表 5 可知， k -近邻剪辑的好坏与 k 和 p 的取值有关。 k 值保持不变， 1p 的值从 0.1
逐渐增大，错误率逐渐增大。因为参考集中的样本个数减少了，参考集决定设计集中的样本
是否要剪掉，参考集的可信赖度关系着分类的结果。
k -近邻剪辑法中要留下一定数量的样本，留下的样本不能太少。样本太少会影响分类
结果，增加错误率。
p
表 5 表明：一般，测试集中的样本数要多于设计集中的样本数(即 1
p
2
)，分类结果
较好。当 k 固定时， 1
p
[0.2,0.4]
，分类结果错误率在 0.097 0.109 之间，且分类结果较
稳定，错误率较小而且波动小； 1
p 后，分类结果都明显变差，还不如直接用最近邻分
0.5
类。当 p 固定，且 1
p
[0.2,0.4]
时， k 在 7 69 之间，分类结果越来越好，错误率变小而
且波动小； [33,69]
k
之间，分类结果最好，错误率最小； 75
k 后，分类结果变差，错
误率高，而且不稳定。
综上，运用 k -近邻剪辑对测试集分类，取 1
p ， [33,69]
k
0.3
分类结果好且稳定，
p
错误率小。 1
0.3,
p
2
时，设计集剪辑留下的样本分布如图 4 所示。
0.7
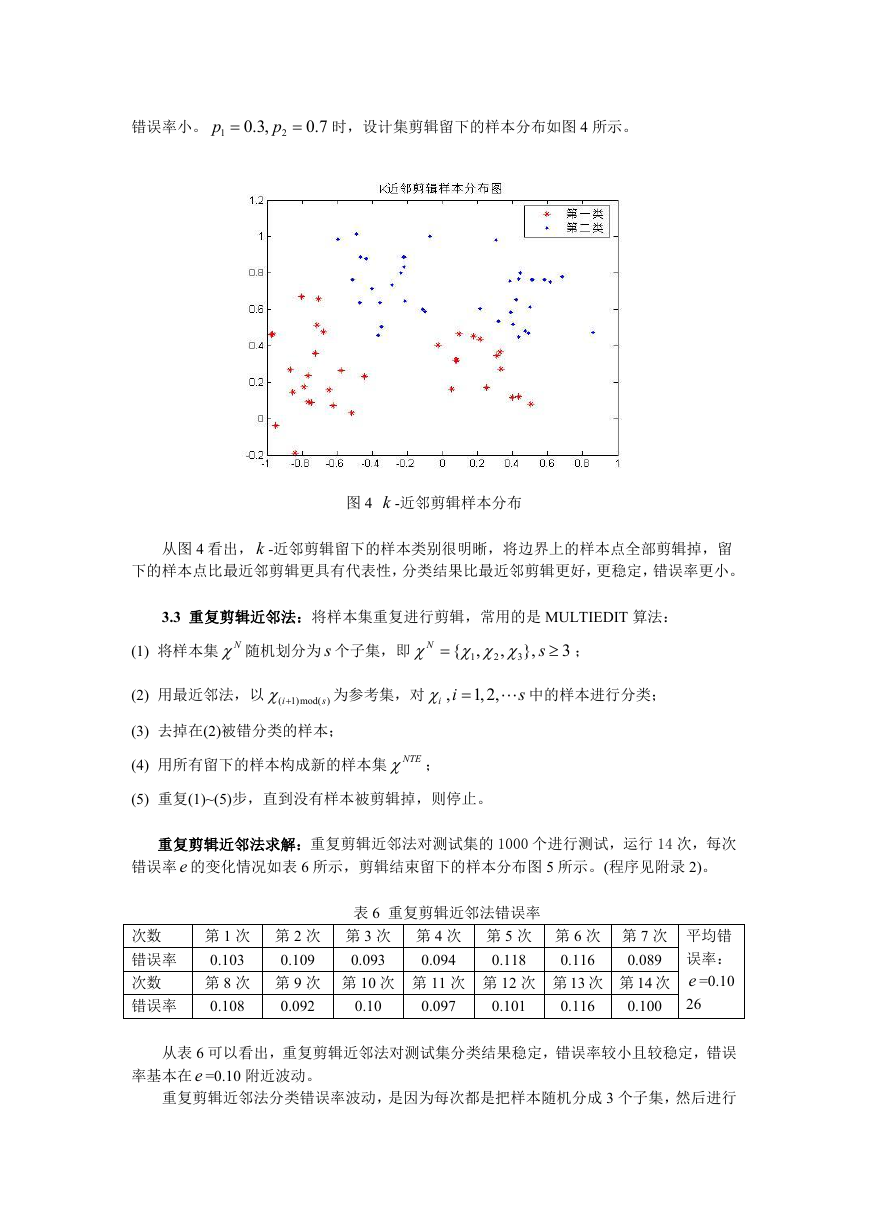
图 4 k -近邻剪辑样本分布
从图 4 看出， k -近邻剪辑留下的样本类别很明晰，将边界上的样本点全部剪辑掉，留
下的样本点比最近邻剪辑更具有代表性，分类结果比最近邻剪辑更好，更稳定，错误率更小。
3.3 重复剪辑近邻法：将样本集重复进行剪辑，常用的是 MULTIEDIT 算法：
(1) 将样本集 N 随机划分为 s 个子集，即
N
3
{ ,
1
,
2
},
s
；
3
(2) 用最近邻法，以 ( 1)mod( )
s
i
为参考集，对 i ,
i
1,2,
中的样本进行分类；
s
(3) 去掉在(2)被错分类的样本；
(4) 用所有留下的样本构成新的样本集 NTE ；
(5) 重复(1)~(5)步，直到没有样本被剪辑掉，则停止。
重复剪辑近邻法求解：重复剪辑近邻法对测试集的 1000 个进行测试，运行 14 次，每次
错误率 e 的变化情况如表 6 所示，剪辑结束留下的样本分布图 5 所示。(程序见附录 2)。
表 6 重复剪辑近邻法错误率
次数
错误率
次数
错误率
第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 第 6 次 第 7 次 平均错
0.103
0.089
误率：
e =0.10
第 8 次 第 9 次 第 10 次 第 11 次 第 12 次 第 13 次 第 14 次
26
0.100
0.108
0.094
0.116
0.097
0.116
0.093
0.118
0.109
0.092
0.10
0.101
从表 6 可以看出，重复剪辑近邻法对测试集分类结果稳定，错误率较小且较稳定，错误
率基本在 e =0.10 附近波动。
重复剪辑近邻法分类错误率波动，是因为每次都是把样本随机分成 3 个子集，然后进行
重复剪辑，两次剪辑留下的样本可能有微小的差别，但对分类的影响不大。
错误率波动小是因为样本进行重复剪辑，随机重复划分，有效避免了划分自己间的相互
作用。剪辑过程中剪掉的是两类边界上的一些样本，剩下的样本形成了两个好的聚类，而且
每个聚类中的样本都属于同一类，它们的分界面十分接近贝叶斯决策面。因此，决策结果是
错误率很小且稳定。
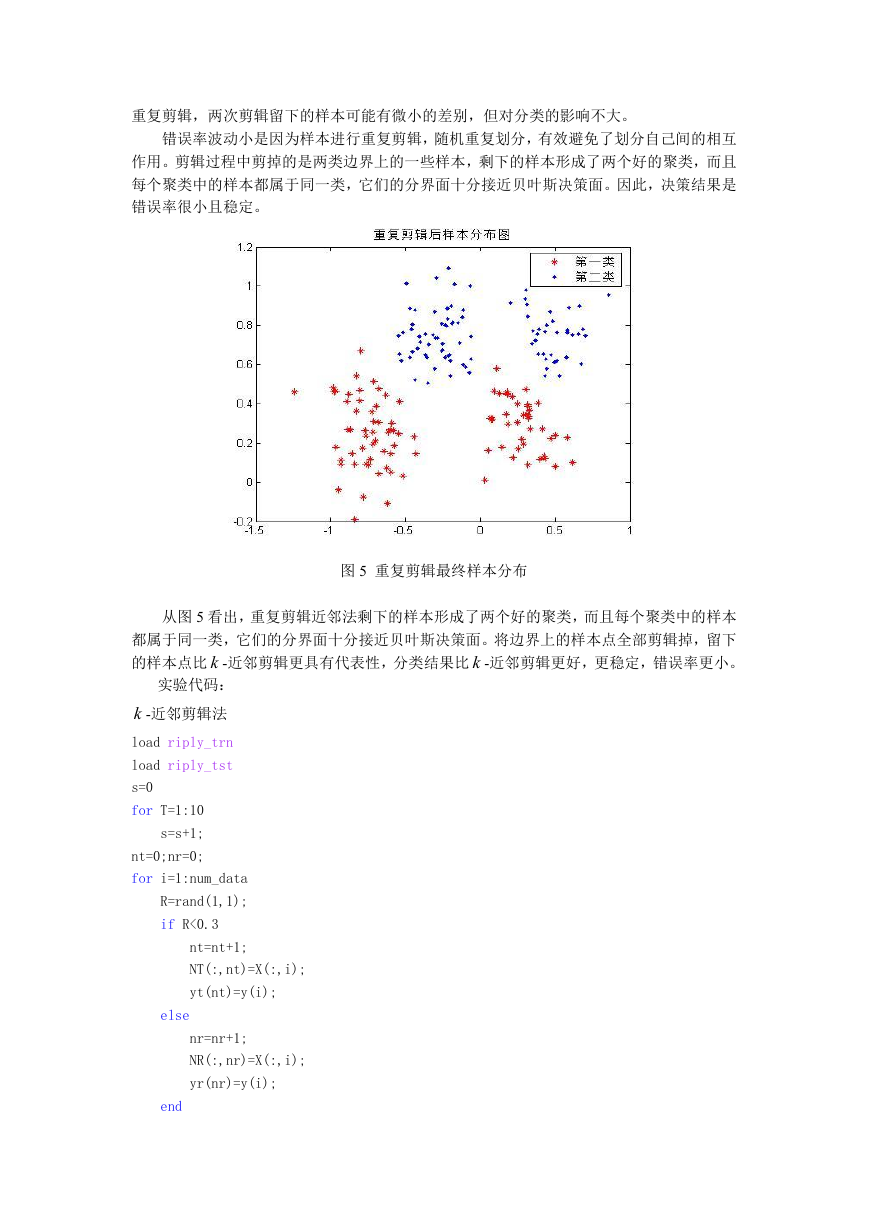
图 5 重复剪辑最终样本分布
从图 5 看出，重复剪辑近邻法剩下的样本形成了两个好的聚类，而且每个聚类中的样本
都属于同一类，它们的分界面十分接近贝叶斯决策面。将边界上的样本点全部剪辑掉，留下
的样本点比 k -近邻剪辑更具有代表性，分类结果比 k -近邻剪辑更好，更稳定，错误率更小。
实验代码：
k -近邻剪辑法
load riply_trn
load riply_tst
s=0
for T=1:10
s=s+1;
nt=0;nr=0;
for i=1:num_data
R=rand(1,1);
if R<0.3
nt=nt+1;
NT(:,nt)=X(:,i);
yt(nt)=y(i);
else
nr=nr+1;
NR(:,nr)=X(:,i);
yr(nr)=y(i);
end
end
for i=1:size(NT,2)
n1=0;n2=0;
for j=1:size(NR,2)
t(:,j)=norm(NT(:,i)-NR(:,j));
end
[tt,k]=sort(t);
for m=1:17 %k的取值======
if
yr(k(m))==1
n1=n1+1;
else
end
n2=n2+1;
end
[x,c]=max([n1 n2]);
if yt(i)~=c
NT(:,i)=[0 0]';
yt(i)=0;
end
end
nt=0;
for i=1:size(NT,2)
if NT(:,i)~=[0 0]'
nt=nt+1;
N_T(:,nt)=NT(:,i);
y_t(nt)=yt(i);
end
end
for i=1:tnum_data
n1=0;n2=0;
for j=1:size(N_T,2)
tr(:,j)=norm(tX(:,i)-N_T(:,j));
end
[tt,k1]=sort(tr);
g(i)=y_t(k1(1));
end
p=find(g~=ty);
er=length(p)/tnum_data;
end
figure, plot(X(1,1:125),X(2,1:125),'r*')
hold on,plot(X(1,126:250),X(2,126:250),'b.')
legend('第一类','第二类')
title('初始样本分布图')
k=length(find(y_t==1));
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
