logo资料库

通过基于L1范数的2D概率PCA进行图像离群值检测和特征提取.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：2.93M 资料格式：pdf 举报 版权申诉
第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
资料共13页，剩余部分请下载后查看
    4834 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 24, NO. 12, DECEMBER 2015 Image Outlier Detection and Feature Extraction via L1-Norm-Based 2D Probabilistic PCA Fujiao Ju, Yanfeng Sun, Junbin Gao, Yongli Hu, and Baocai Yin paper an introduces Abstract— This L1-norm-based probabilistic principal component analysis model on 2D data (L1-2DPPCA) based on the assumption of the Laplacian noise model. The Laplacian or L1 density function can be expressed as a superposition of an infinite number of Gaussian distributions. Under this expression, a Bayesian inference can be established based on the variational expectation maximization approach. All the key parameters in the probabilistic model can be learned by the proposed variational algorithm. It has experimentally been demonstrated that the newly introduced hidden variables in the superposition can serve as an effective indicator for data outliers. Experiments on some publicly available databases show that the performance of L1-2DPPCA has largely been improved after identifying and removing sample outliers, resulting in more accurate image reconstruction than the existing PCA-based methods. The performance of feature extraction of the proposed method generally outperforms other existing algorithms in terms of reconstruction errors and classification accuracy. Index Terms— L1-norm, probabilistic principal component analysis, variational Bayesian inference, outlier detection, feature extraction. I. INTRODUCTION H IGH-DIMENSIONAL and multiple array data are widely acquired in modern computer vision research. This high-dimensionality of data not only increases computa- tional overhead and memory requirements in algorithms, but also adversely affects their performance in real applications. However, high-dimensional data are not often distributed uni- formly in their ambient space, instead they lie in or close to a low-dimensional space or manifold [23], [33]. Finding the low- dimensional embedding for high-dimensional observed data has been a challenging problem in machine learning research. However, much progress has been made towards building tools or algorithms for dimensionality reduction in the last couple of decades [3], [8], [11], [17]. Principle Component Analysis (PCA) [2] is one of popular dimensionality reduction methods widely used in image analysis [7], [10], pattern recognition [6], [18] and machine learning [13] for data analysis. PCA can be interpreted in many ways, one of which assumes that the observed high- dimensional data are generated from their low-dimensional factors through a linear model with the corruption of Gaussian noise, i.e., measured by the L2-norm. Traditional PCA is concerned with vectorial data and has been very successful in applications [13], [28]. Today data emerging from science and technology are in new types with more structures. For example, image data should be regarded as 2D tensors in order to preserve their 2D spatial information. In order to apply the classical PCA to such 2D image data, a typical workaround is to vectorize 2D data. Vectorizing 2D data not only preserves the high-dimensionality of data, causing the problem of the curse of dimensionality [25], but also ignores valuable information about the spatial relationships among 2D data. for Further, feature extraction or the data-as-vector PCA approach will be sub- optimal representation because of spatial information loss. Instead of using vectorization, PCA approaches for two-dimensional data (2DPCA) have been proposed [24], [27]. Compared with the traditional PCA, 2DPCA directly conducts analysis on 2D data matrices so that the structural relation between data entries can be preserved and more spatial information can be utilized [12], [20], [30]. Numerous experiments have shown that 2DPCA with less parameters can achieve competitive or even better recognition performance than PCA, especially when the sample size is small relative to feature dimensionality. Similar to the conven- tional PCA, 2DPCA models are also based on the L2-norm error measurement. Manuscript received December 31, 2014; revised May 27, 2015; accepted August 7, 2015. Date of publication August 17, 2015; date of current version September 18, 2015. This work was supported in part by the Natural Science Foundation of Beijing, China, under Grant 4132013, in part by the Australian Research Council Discovery Projects Funding Scheme under Grant DP130100364, and in part by the National Natural Science Foundation of China, under Grant 61171169, Grant 61133003, Grant 61370119, and Grant 61390510. The associate editor coordinating the review of this manu- script and approving it for publication was Dr. Christopher Wyatt. F. Ju, Y. Sun, Y. Hu, and B. Yin are with the Beijing Key Laboratory of Multimedia and Intelligent Technology, College of Metropolitan Transportation, Beijing University of Technology, Beijing 100124, China (e-mail: jufujiao2013@emails.bjut.edu.cn; yfsun@bjut.edu.cn; huyonglig@ bjut.edu.cn; ybc@bjut.edu.cn). J. Gao is with the School of Computing and Mathematics, Charles Sturt University, Bathurst, NSW 2795, Australia (e-mail: jbgao@csu.edu.au). Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org. Digital Object Identifier 10.1109/TIP.2015.2469136 There exist a number of models for deriving PCA, the majority of which are algebraic. Algebraic models don’t have the flexibility of providing confidence information of the model when dealing with noisy data. To combat this drawback, Tipping and Bishop [22] proposed a probabilistic PCA model, called PPCA. In PPCA, observed data are regarded as random variables, generated from a set of latent random variables which follow the Gaussian distribution of zero mean and identity covariance, with additive noises following a Gaussian distribution with zero mean and an isotropic covariance. PPCA is a special case of the standard factor analysis (FA) model [2] whose noise follows Gaussian distribution with zero mean and diagonal covariance. Under the probabilistic learning framework, the model parameters in PPCA can be easily solved by the maximum likelihood estimation (MLE). 1057-7149 © 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
    JU et al.: IMAGE OUTLIER DETECTION AND FEATURE EXTRACTION VIA L1-NORM-BASED 2D PROBABILISTIC PCA 4835 Furthermore, PPCA can be used to deal with the cases containing missing values within the observed data, while the traditional PCA is not valid in missing value cases. Recently, Zhao et al. [34] proposed a probabilistic principle component analysis model on 2D data, called 2DPPCA, which takes a step forward for PPCA model in 2D cases. A Gaussian noise distribution is assumed in both the afore- mentioned PCA (implicitly) and PPCA (explicitly) methods. However real-life data often contain noises which may not follow Gaussian distributions, particularly in the cases of existing outliers such as partial occlusion in scene images. In such cases, both PCA and PPCA may produce a biased model for data as the model will try to fit data under the Gaussian noise assumption. It has been well known that the Laplacian distribution (or L1 distribution) is less sensitive to outliers compared with the Gaussian distribution. So it is a natural development to use L1-norm as the error metric to replace the L2-norm measure- ment used in both PCA and PPCA methods. There have been many approaches proposed to include L1-norm or L1 dis- tribution in an attempt to deal with data outliers. To the best of our knowledge, Zhong and Zhang [36] proposed a robust LDA instead of conventional LDA using L2-norm. Baccini et al. [1] proposed the first L1-norm PCA (L1-PCA) model. Meng et al. [19] proposed an L1-PCA model by max- imizing the so-called L1 dispersion, while Ke and Kanade [9] formulated L1-PCA by maximum likelihood estimation. They use either heuristic estimate or weighted median method and convex programming to obtain the projection matrix of L1-PCA. All of in the alge- braic framework with expensive computational cost and no invariance to rotations. Aiming to diminish this drawback, Kwak [14] proposed a fast and robust L1-norm PCA method, termed as PCA-L1. Similar to [19], PCA-L1 replaces maxi- mizing L2-norm based variance with L1-norm dispersion in the feature space to realize robust and rotation invariant PCA. Ding et al. [4] further extended L1-norm PCA to the R1-norm (a modified L1-norm) based PCA (R1-PCA). It combines the merits of L2-PCA and L1-PCA. The model is guaranteed to be rotational invariant, however the convergent speed of the algorithm is relatively slow. Li et al. [16] investigated the implementation of fast PCA-L1 [14] for 2D data by simply considering PCA-L1 model on multiple phases of 1D data from 2D data. This method is robust to outliers because of utilizing the L1-norm errors metric, and more information regarding spatial relationships can be preserved. the above mentioned models fall Concerned with a probabilistic model for L1-PCA, Gao [5] introduced a robust probabilistic L1-PCA model, called L1-PPCA. In order to provide an effective learning algorithm, the author expanded the Laplacian distribution as a superpo- sition of infinite number of Gaussiann distributions so that this model can be solved by using variational Expectation Maximization (EM)-type algorithms. Motivated by L1-PPCA, we propose a probabilistic PCA model for 2D data (L1-2DPPCA) in this paper. The con- tributions of the paper are three-fold. Firstly, in generalizing L1-PPCA for 2D data, we formulate the error distribution in terms of the Hadamard product to facilitate the variational EM algorithm in dealing with the difficulty imposed by using the multiple linear model, referring to equation (1). Secondly, an analysis is given as the foundation for proposing an indicator for outlier detection or identification, and finally a strategy of using Gaussian distribution as approximated posterior for the latent feature variables is proposed to over- come the difficulty of non-Gaussian posterior in the variational EM algorithm. L1-2DPPCA has three major advantages: 1) The model makes use of structural information within 2D data and can be easily extended for high order tensorial data. All the algorithm derivations remain without any major difficulty. 2) The model is robust to grossly noises such as occlusion in images and can be used as a stable outlier detector. It can be also generalized to other noise models like student-t distribution. And 3) The model uses less parameters than the vectorized L1-PPCA, thus it requests less data for training. the paper is organized as follows. In Section II, L1-2DPPCA model is introduced. The vari- ational approximation technology for solving L1-2DPPCA model is derived and presented in Section III and Appendix. In Section IV, some experimental results are presented for evaluating the performance of the proposed model. Finally, conclusions are summarized in Section V. The remainder of II. L1-2DPPCA MODEL Let X = {X1, X2, . . . , XN} be N independent and iden- tically distributed random variables with values in Rm×n. The probabilistic second-order PCA (PSOPCA) [32] is based on the matrix-variate normal assumption and assumes the following two-sides latent variable model: Xk = LZkRT + M + Ek, (1) where L in size m × r and R in size n × c are the row and column loading matrices, and Zk is the latent core variable of Xk, with r (≤ m) rows and c (≤ n) columns, respectively. M and Ek both in size m × n are the mean matrix and the error matrix, respectively. Zk is regarded as the latent representation of the observed data Xk, so the model can be used as a feature extractor or dimensionality reduction through a Bayesian inference process. as the the article Without loss of generality, suppose M is a zero matrix input data X can be throughout learning. Denote by N (X|M, U, V) centralized in model the matrix-variate Gaussian distribution with the mean M and row covariance U and column covariance V [26]. If Ek ∼ N (Ek|0, σ Im , σ In), i.e., for each error compo- nents i j ∼ N (i j|0, σ 2)(i = 1, 2, . . . , m; j = 1, 2, . . . , n), then model probabilistic 2DPCA [31]. standard leads (1) to the Although the conventional PCA based on L2-norm has been successful for many applications, it is vulnerable to the presence of outliers, because the effect of the outliers with a large norm is exaggerated by the use of L2-norm. Outliers exist widely, perhaps representing corrupted observations or genuine samples from a heavy-tailed noise process. To cope
    4836 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 24, NO. 12, DECEMBER 2015 with outliers in a 2D data set and estimate model confidence levels, we introduce an L1-norm based 2D probabilistic PCA, noted by L1-2DPPCA. We consider that the error component i j is independent and identically distributed according to a centered Laplacian distribution whose density function is given by pL1 (|σ ) = 1 2σ exp − 1 σ || . (2) 1 pL1 Based on the above equation, the joint distribution of all the components of Ek can be written as, due to the independence of the error component, (Ek|σ ) = (2σ )mn exp |. |e(k) n j=1 where Ek1 = − 1 σ Ek1 To develop a generative Bayesian model, we define a Gaussian prior distribution p(Zk) over the latent variable. Specifically, the prior distribution over Zk is given by the following zero-mean unit-covariance matrix-variate Gaussian distribution: p(Zk) = N (Zk|0, Ir , Ic) = rc tr(ZT m i=1 exp (3) i j , . 2 k Zk ) − 1 2 1 2π To model noise levels, we impose a prior Gamma distribu- tion on ρ = 1/σ 2 instead of directly on σ in equation (3): (4) ρ ρaρ−1exp{−bρρ}. pσ (ρ) = (ρ|aρ , bρ) = baρ (aρ ) (5) For the sake of convenience, let Z = {Z1, . . . , ZN} denote the model hidden variables, and  collect all the model parameters L and R, etc. For the given observation X , the log likelihood can be defined by its marginalized log likelihood over the assumed latent variables Z and ρ L() = log p(X|) = log p(X , Z, ρ|)dZdρ. (6) ρ Z Then the learning task is to learn model parameters  ( = {L, R}) such that p(X|) in (6) is maximized. A gen- eral approach is to use the EM algorithm [2], where we need to calculate the posterior over latent variables p(Z, ρ|X , ) in the E-step and estimate model parameters  in the M-step. the unknowns is, by The posterior distribution over all applying Bayes’ rule, , p(Z, ρ|X , ) = p(X , Z, ρ|) p(X|) (7) where p(X , Z, ρ|) is the joint distribution of the data set X , the latent variable Z, and the hidden parameters ρ. Under the model assumptions (3), (4) and (5), the joint distribution is given by p(X , Z, ρ|) = N Unfortunately, we cannot compute the posterior analytically as the denominator p(X|) in (7) necessitates an intractable (Xk − LZkRT|σ ) p(Zk) pσ (ρ). k=1 pL1 (8) integration due to the Laplacian distribution pL1. A direct application of EM is not feasible. Therefore, we propose a variational approximation scheme in the next section. III. VARIATIONAL APPROXIMATION FOR L1-2DPPCA Under the variational EM framework, instead of using the exact posterior (7) in the EM algorithm, one uses an approx- imated distribution Q(Z, ρ), called variational distribution, over the hidden variables. For any distribution Q(Z, ρ), the following lower bound on L() is guaranteed: p(X , Z, ρ|)dZdρ L() = log ≥ Z ρ − Z ρ Q(Z, ρ)log p(X , Z, ρ|)dZdρ Q(Z, ρ)logQ(Z, ρ)dZdρ Z ρ F (Q(Z, ρ), ). The first step of this derivation is based on Jensen’s inequality, referring to [2] for more details. When Q(Z, ρ) is equal to the true posterior p(Z, ρ|X , ) given the data set X , it can be proved that F (Q(Z, ρ), ) = L(). The purpose of the variational EM [2] is to maximize F (Q(Z, ρ), ) with respect to Q(Z, ρ) and . In order to have a tractable variational EM algorithm, it is a common practice to assume a fully factorized distribution to approx- imate the true posterior, e.g., Q(Z, ρ) = Q(Z)Q(ρ) in this case. A. Reforming the Model Although the variational EM algorithm suggests maximizing F (Q(Z, ρ), ) instead of maximizing likelihood L() for an approximated posterior distribution Q, it is still a challenge to have an appropriate approximated method in our case. The use of Laplacian distribution in (3) makes it hard to find or define a good approximation to the posterior of Z. Fortunately Laplacian distribution (2) can be expanded as a superposition of infinite number of Gaussian distributions given by the following relation [21], (|σ ) = pL1 ∞ 0 β 2π σ 2 exp with p(β) = 1 2 β−2exp − β 2σ 2 − 1 2β 2 η(β)dβ, (9) . (10) Both (9) and (10) promote introducing an extra hidden random variable β. Thus the likelihood function can be written in terms of newly introduced random variable β’s as follows, refer to (8), p(X|) = Z β ρ Z β ρ = p(X , Z, β, ρ|)dZdβdρ (Ek|σ, βk) p(βk) pL1 × p(Zk) pσ (ρ)dZdβdρ, k
    JU et al.: IMAGE OUTLIER DETECTION AND FEATURE EXTRACTION VIA L1-NORM-BASED 2D PROBABILISTIC PCA 4837 ] where βk = [β(k) is a matrix variable associated with each sample Xk with the same dimension as Xk. Each element of βk is independent and follows the same distribution (10). So i j p(βk) = ) = p(β(k) i j )−2exp 1 2 (β(k) i j − 1 2β(k) i j i j i j In additional, (Ek|σ, βk) = pL1 = i j β(k) i j 2π σ 2 exp{− β(k) i j 2σ 2 )2} ((k) i j β(k) i j i j (2π σ 2)mn exp 2σ 2 tr[ET − 1 k (Ek ◦ βk)] where ◦ represents Hadamard product, which facilitates the derivation of the final variational EM algorithm for the proposed model. The definition of p(Zk) and pσ (ρ) is shown in (4) and (5). So the likelihood function becomes p(X|) = )−2exp . , j i k β ρ Z β(k) × i j (2π σ 2)mn exp mn − 1 × 2 1 2π exp i j 2 − 1 2β(k) i j (Ek ◦ βk)] 1 2 (β(k) i j 2σ 2 tr[ET − 1 k tr(ZT k Zk) pσ (ρ)dZdβdρ. (11) B. Variational EM Algorithm The reformed L1-2DPPCA model p(X|) defined in (11) involves two matrix-variate Gaussian distributions over Ek and Zk, one Gamma distribution over ρ and a number of inverse Gamma distributions over β(k) i j ’s. A tractable vari- ational EM algorithm can be proposed if the approximated posterior Q is restricted to the family of Q(Z, β, ρ) = Q(Z)Q(β)Q(ρ) with independent components for the hidden variables Z, ρ and β. Then maximizing the variational func- tional F with respect to Q(Z), Q(β) and Q(ρ) results in the following alternative procedure. A complete derivation is given in Appendix. E-Step: In E-step, we update Q-distributions of all hidden values parameter current fixed the variables with for L and R. 1) Updating Q(Zk): Under the assumption of a separable approximated posterior, it can be proved that the variational solution for the posterior distribution of Zk given Xk is in gen- eral not matrix-variate Gaussian. To get a tractable posterior in the variational EM, we restrict the approximated variational distribution to be a matrix-variate Gaussian N (Zk|Bk, Tk , Sk) to approximate the true posterior with the mean Bk in size r × c and covariances Tk 0 of size r × r and Sk 0 of size c × c, respectively. In the variational E-step, it turns out that the variational parameters Tk and Sk satisfy i, j Tk = cσ 2( Sk = r σ 2( β(k) i j (r j Skr T j β(k) i j (li TklT i i li + σ 2tr(Sk)Ir )−1, )lT j r j + σ 2tr(Tk)Ic)−1 )r T (12) (13) i, j where li represents the i-th row of the row loading matrix L and r j represents the j-th row of the column loading matrix R. Parameter Bk satisfies i liBkr T j r j + σ 2Bk = β(k) i j x (k) i j lT β(k) i j lT i r j . (14) i, j i, j To solve (14) for Bk, we can make a vectorization on both sides and solve a linear equation j r j ⊗ (β(k) i j lT r T i li ) + σ Ic ⊗ σ Ir )vec(Bk) = y, (15) ( i, j where y = vec( β(k) i j x (k) i j lT be reshaped back to get Bk. i, j 2) Updating Q(β): The best Q i r j ). The solution vec(Bk ) can ∗(β) distribution can be expressed as, by using the similar derivation as in [22], ∗(βk) = EZ,ρ[log p(X , Z, βk, ρ|L, R)] + const log Q ∗(β(k) It says that the log of the optimal solution for latent variable βk is obtained simply by considering the log of the joint distribution over all hidden and visible variables and then taking the expectation with respect to all the other latent variables. From the above equation, we can get + β(k) − 1 , 2 exp 2 − liZkr T ∗(β(k) where ψ (k) )2. In fact, the best Q is a special case, with λ = − 1 2 , χ = 1 and ϕ = ρψ (k) i j , of the so-called generalized inverse Gaussian distribution defined by G(β(k) i j ) ∝ (β(k) = EZk (1/β(k) i j ρψ (k) i j (x (k) i j )− 3 Q i j i j i j i j i j ) ) j )λ−1exp (β(k) i j (χ /β(k) i j + ϕβ(k) i j ) , |λ, χ , ϕ) = (ϕ/χ )λ/2 √ χ ϕ) 2Kλ( − 1 2 where Kλ(x) is the modified Bessel function of the second kind. It is easy to show ∞ 0 = β(k) i j β(k) i j Q ∗(β(k) i j )dβ(k) i j = 1 ρψ (k) i j . (16) 3) Updating Q(ρ): The best Q distribution (ρ|aρ, bρ) but with the updated parameters: ∗(ρ) is still a Gamma aρ = aρ + mn N 2 bρ = bρ + 1 ψ, 2 ψ (k) i j . β(k) i j where ψ = k,i, j , (17) (18) M-Step: In the M-step, we fix all the distributions over the hidden variables and update the parameters L and R by maximizing F (Q(Z, ρ), ) with respect to  or equivalently minimizing the robust reconstruction error of data points.
    4838 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 24, NO. 12, DECEMBER 2015 Algorithm 1 Variational EM Algorithm for L1-2DPPCA D. Identifying Data Outliers and Feature Extraction Let us go back to (11) and look at the term related to the error p(Ek) ∝ exp − 1 2σ 2 tr[ET k (Ek ◦ βk)] . If there are some outliers in training set, the reconstruction error tr(ET k Ek) of these outliers will be significantly larger than the errors of other data points. To maintain a relatively better likelihood p(Ek), the latent variables βk associated with these outliers will adopt themselves to fit appropriate likelihoods, which means it is likely that relevant elements of learned βk have smaller values than that for other data. Hence βk can be seen as a reasonable outlier indicator. The smaller the βk value is, the more likely the associated data Xk contains outlier components. This is one of benefits arising from introducing the extra latent variables when dealing with Laplacian distribution. The numerical experiment in the next section confirms our theoretical analysis. After training the model, we can easily infer Z and β for the unseen data X by fixing the M-step with the learned model parameters L and R in Algorithm 1. We refer to this Bayesian inference procedure as feature extraction or dimensionality reduction for data X. IV. EXPERIMENTAL RESULTS AND ANALYSIS In this section, we conduct several experiments on hand- written digits, face databases and the ETH80 database to assess the proposed model. These experiments are designed to demonstrate the practical significance of the introduced latent variables β, whose values may imply the existence of outlier data, and to show the performance of the proposed L1-2DPPCA in feature extraction and reconstruction by com- paring with other existing models and algorithms. All the algorithms are coded by Matlab 2014a and implemented on an Intel Core i5-3470K 3.20GHz CPU machine with 6G RAM. The relevant PCA algorithms that can be fairly compared against our proposed L1-2DPPCA are GLRAM (Generalized [29], PSOPCA Low Rank Approximations of Matrices) (Probabilistic L1-2DPCA (the unilateral-projection scheme) [16] and L1-B2DPCA (the bilateral-projection scheme) [35]. As the L1-2DPCA uses more parameters to represent an image (2D data), for a fair comparison, the bilateral-projection scheme L1-B2DPCA is used. Because the zero-noise PSOPCA model and GLRAM have the same stationary point [32], we only compare with GLRAM. Second-Order PCA) [32], A. Data Preparation and Experiment Setting All of the experiments are conducted on four publicly available datasets: database (http://yann.lecun.com/exdb/mnist). • A subset of handwritten digits images from the MNIST • The Yale face database (http://vision.ucsd.edu/content/ yale-face-database). • The ORL face (http://www.cl.cam.ac.uk/ database research/dtg/attarchive/facedatabase.html). 4) Updating L and R: we maximize the lower bound F with respect to factor loadings L and R to get: li =[ +Bkr T )]−1, (Tkr j Skr T j j r j BT k β(k) i, j x (k) i j r j BT k ][ β(k) i, j k, j k, j and r j = [ k,i β(k) i j x (k) i j liBk][ k,i (19) β(k) i j (SkliTklT i + BT i liBk )]−1. k lT (20) The overall variational EM algorithm is to alternate between E-step and M-step iteratively. To terminate the iteration, up to a given maximum iterative number T , we use the following stopping condition: Lt+1Bt+1Rt+1 − Lt BtRtF /N < , where  is a given value, N is the number of training samples. The final variational EM algorithm is summarized in Algorithm 1. C. Algorithm Complexity Analysis The proposed L1-2DPPCA algorithm has time complexity O(tmn N(cr )2), which is given in Appendix. Here, t is the actual number of EM iterations, m and n are the size of sample image, r and c are the reduced dimension size and N is the number of all samples. The general probabilistic second-order PCA (PSOPCA) [31] has the time complexity O(tmn N max(r, c)). PSOPCA is a probabilistic two-order PCA based on L2 norm. It is obvious that the proposed algorithm has more time complexity than PSOPCA owing to introducing the new latent variable βk. The latent variable βk provides extra information for outlier identification as described in the next subsection.
    JU et al.: IMAGE OUTLIER DETECTION AND FEATURE EXTRACTION VIA L1-NORM-BASED 2D PROBABILISTIC PCA 4839 Fig. 1. Digit 5 images with added noises. Fig. 2. Sample images from the Yale face database. Fig. 3. Some generated outlier face images in the training set from the Yale face database. • The ETH80 database libpmk/samples/eth.html). (http://people.csail.mit.edu/jjl/ All handwritten digits images are in grayscale and have a uniform size of 28 × 28 pixels. In our experiment, digit 5 was taken as an example, for which 50 images are chosen as training data. We added additional 9 corrupted images of the digit 5 into the training dataset and they are shown in Fig. 1. The noise is generated from a uniform distribution on the interval [10, 600], and then the corrupted images are scaled to the standard gray levels from 0 to 255. All images are centralized. face contains 15 database The Yale individuals, with 11 images for each individual. The images were captured under different illumination and expression conditions. Some sample images are shown in Fig. 2. We select 8 images of each individual as training samples (120 images), while the remaining images are used for testing (for computing reconstruction error and recognition rate). 30 images in the training set are used to generate the outliers. These outliers are formed by adding rectangle noise. The size of the rectangles ranges from 30 × 30 to 50 × 50. Within each rectangle, the pixel value is randomly set to be either 0 or 255. Fig. 3 shows some samples of the outliers. All images are grayscale and scaled to a resolution of 64 × 64 pixels. Fig. 4. Sample images from the ORL face database. The ORL face database includes 40 distinct individuals with 10 images for each individual. For some individu- als, the images were taken at different times, illumination changes, facial expressions variation (open / closed eyes, smiling / not smiling) and facial details (glasses / no glasses). Some sample images are shown in Fig. 4. 320 images of 40 individuals are used for training, while the remaining images are used for testing (for computing reconstruction error and recognition rate). Two images of each individual are used to generate outliers. The formation of rectangle noise is the same as that experiment on Yale database. All images are grayscale and normalized to a resolution of 64 × 64 pixels. The public ETH80 database consists of 8 ground truth object categories, each consisting of 10 different instances (see Fig. 6) from 41 different views, for a total of 3280 images. These objects undergo severe view point change, posing significant challenges to recognition due to the high intra-class diver- sity. More details about the database can be found in [15]. We randomly partitioned 41 images of different views into two sets: 21 images of all objects for training (21 × 10 × 8) and 20 images for testing (20 × 10 × 8). In the training set, two images of each object are used to generate rectangle outliers. The formation of rectangle noise is the same as that experiment on Yale database. All images are made to grayscale and normalized to a resolution of 64 × 64 pixels. In all the experiments we set aρ = 0.5, bρ = 0.1,  = 0.15 and T = 100. The initial components of all β’s are set to 1 and initial loading matrices L and R are given randomly. B. Indicating Outliers This experiment aims at illustrating the practical meaning of β and evaluating the effect of detecting outliers. 1) Handwritten Digits Image Set: According to the analysis in Section III, we know that all elements of those βk associated with data outliers are significantly smaller than the values for other points. Thus we can judge whether the k-th sample is an outlier by the mean value of all elements in βk. For other L1-norm based non-probabilistic PCA methods, it identifying outliers by using reconstruction errors. The reconstruction errors associated with the data outliers are usually larger than that of other points. is a natural choice for Next we compare outlier detection performance of the proposed L1-2DPPCA and non-probabilistic L1-B2DPCA.
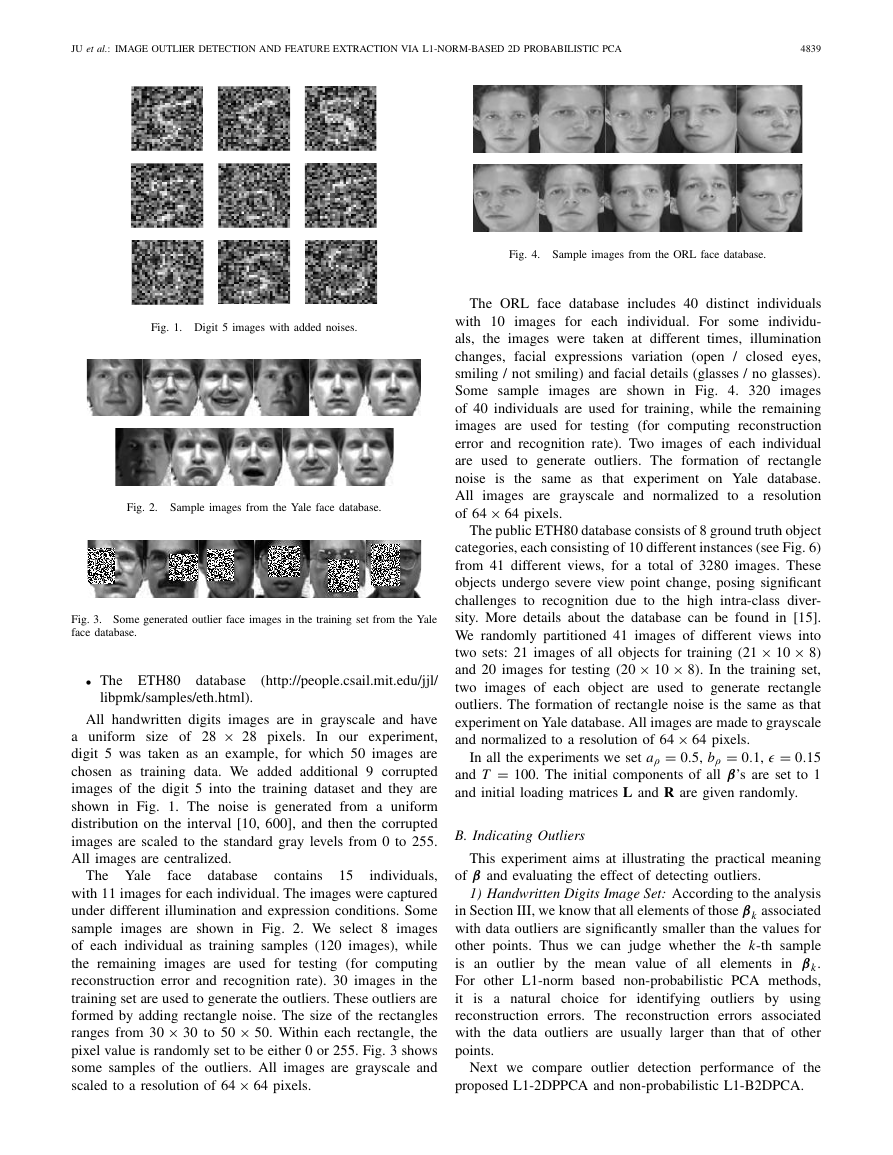
    4840 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 24, NO. 12, DECEMBER 2015 Fig. 5. Outliers detection with βk on training set. The first row is detecting outliers by computing reconstruction errors using L1-B2DPCA. The second row is detecting outliers by the mean of βk using L1-2DPPCA. The reduced dimensions are respectively 1, 5 and 10 from the first column to third column. Fig. 6. Each object category in the ETH80 database contains 10 different objects, such as dog. Fig. 5 shows the reconstruction errors and the means of βk for all the samples. The first row shows reconstruction errors using L1-B2DPCA and the second row demonstrates the means of βk given by the proposed L1-2DPPCA when the reduced dimension is 1, 5 and 10 respectively. We can see from this figure that the means of βk given by L1-2DPPCA have a significant clear difference between the clean samples and cor- rupted samples in the cases of reduced dimension 1, 5 and 10, respectively. Similar phenomena can be observed for other dimensions. The results from L1-B2DPCA, in the cases of reduced dimensions 1 and 5, demonstrate that simply using reconstruction errors cannot discriminate outlier samples from the clean samples. 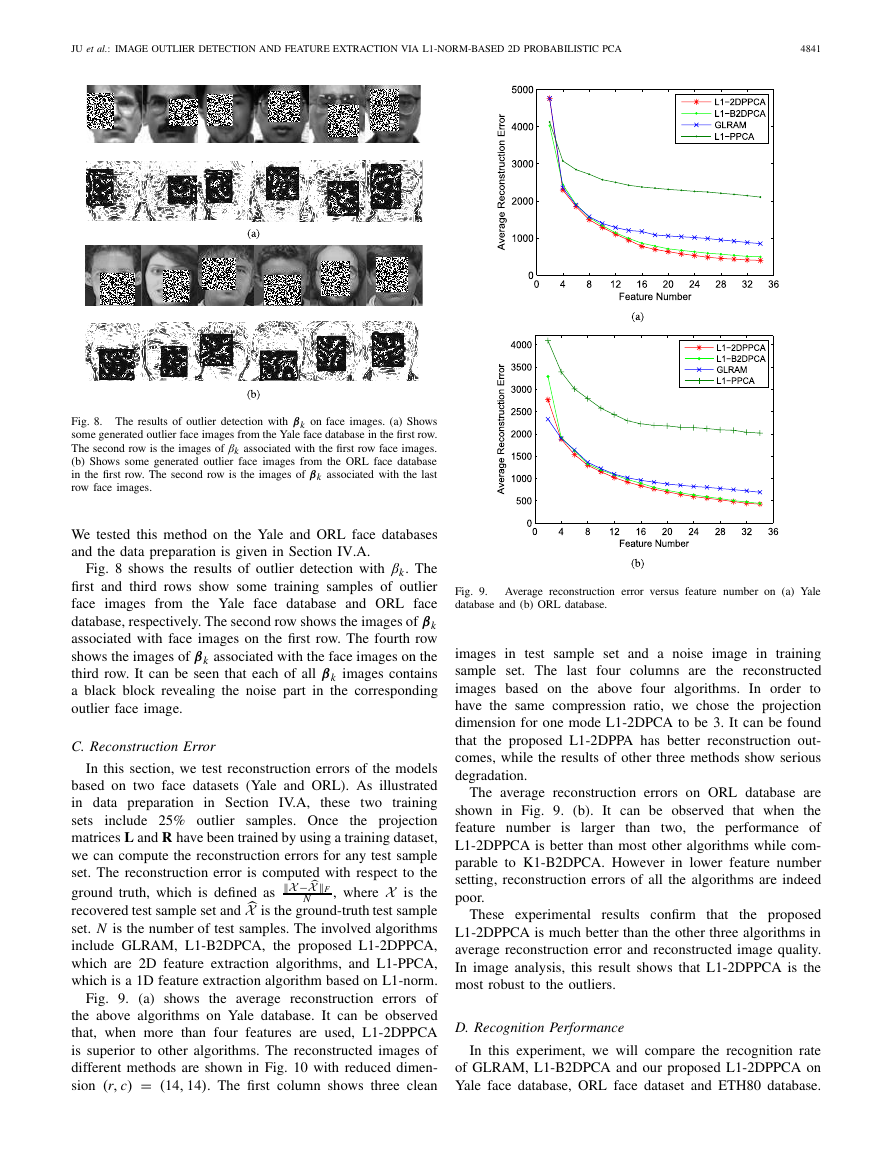For our purposes below, denote the original data set as Dataset-I and the new data set after removal of outliers as Dataset-II. We test the quality of these two datasets. We train the standard PCA on both Dataset-I and -II respec- tively to assess the impact of removing data outliers. The first three principal components based on these two training data sets are shown in Fig. 7, respectively. The first row is the Fig. 7. Experimental results for standard PCA training on Dataset-I and Dataset-II. The first row is the first three principal components training on the Dataset-I. The second row is the first three principal components training on the Dataset-II. first three principal components obtained from Dataset-I while the second row is those from Dataset-II. It is no surprise that the first two principal components under the Dataset-I contain noise components as PCA tries to explain noise information in learning the model. However the principal components trained on Dataset-II look better. Our conclusion is that the proposed L1-2DPPCA method can be safely used as an outlier identifier with relevant accuracy. This suggests we may use L1-2DPPCA method as a pre-processing step for other learning algorithms which will cull possible outliers from a dataset. 2) Face Image Databases: In the last experiment, a cor- rupted handwritten image is seen as an outlier of the training set. In this experiment, we generated noise on a small part of an image instead of the whole image, such as Fig. 3. These corrupted pixels can also be seen as outliers. Next we want to detect the position of the noise by showing the image of βk.
    JU et al.: IMAGE OUTLIER DETECTION AND FEATURE EXTRACTION VIA L1-NORM-BASED 2D PROBABILISTIC PCA 4841 Fig. 8. The results of outlier detection with βk on face images. (a) Shows some generated outlier face images from the Yale face database in the first row. The second row is the images of βk associated with the first row face images. (b) Shows some generated outlier face images from the ORL face database in the first row. The second row is the images of βk associated with the last row face images. We tested this method on the Yale and ORL face databases and the data preparation is given in Section IV.A. Fig. 8 shows the results of outlier detection with βk. The first and third rows show some training samples of outlier face images from the Yale face database and ORL face database, respectively. The second row shows the images of βk associated with face images on the first row. The fourth row shows the images of βk associated with the face images on the third row. It can be seen that each of all βk images contains a black block revealing the noise part in the corresponding outlier face image. C. Reconstruction Error In this section, we test reconstruction errors of the models based on two face datasets (Yale and ORL). As illustrated in data preparation in Section IV.A, these two training sets include 25% outlier samples. Once the projection matrices L and R have been trained by using a training dataset, we can compute the reconstruction errors for any test sample set. The reconstruction error is computed with respect to the , where X is the recovered test sample set and X is the ground-truth test sample ground truth, which is defined as X− XF N set. N is the number of test samples. The involved algorithms include GLRAM, L1-B2DPCA, the proposed L1-2DPPCA, which are 2D feature extraction algorithms, and L1-PPCA, which is a 1D feature extraction algorithm based on L1-norm. Fig. 9. (a) shows the average reconstruction errors of the above algorithms on Yale database. It can be observed that, when more than four features are used, L1-2DPPCA is superior to other algorithms. The reconstructed images of different methods are shown in Fig. 10 with reduced dimen- sion (r, c) = (14, 14). The first column shows three clean Fig. 9. database and (b) ORL database. Average reconstruction error versus feature number on (a) Yale images in test sample set and a noise image in training sample set. The last four columns are the reconstructed images based on the above four algorithms. In order to have the same compression ratio, we chose the projection dimension for one mode L1-2DPCA to be 3. It can be found that the proposed L1-2DPPA has better reconstruction out- comes, while the results of other three methods show serious degradation. The average reconstruction errors on ORL database are shown in Fig. 9. (b). It can be observed that when the feature number the performance of L1-2DPPCA is better than most other algorithms while com- parable to K1-B2DPCA. However in lower feature number setting, reconstruction errors of all the algorithms are indeed poor. than two, is larger These experimental results confirm that the proposed L1-2DPPCA is much better than the other three algorithms in average reconstruction error and reconstructed image quality. In image analysis, this result shows that L1-2DPPCA is the most robust to the outliers. D. Recognition Performance In this experiment, we will compare the recognition rate of GLRAM, L1-B2DPCA and our proposed L1-2DPPCA on Yale face database, ORL face dataset and ETH80 database.
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料