logo资料库

论文研究-基于博弈论的快速收敛功率控制算法研究 .pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.47M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 基于博弈论的快速收敛功率控制算法研究# 袁骥德，赵旦峰** （哈尔滨工程大学信息与通信学院，哈尔滨 150001） 5 摘要：以 CDMA 网络系统以作为认知无线电通信平台，针对系统中不同认知用户的通信需求， 提出了新的非合作功率控制博弈算法，并证明了该算法纳什均衡的存在性和唯一性。仿真结 果表明，该算法具备较快的收敛速度，并能很好的抑制认知用户间的互干扰，能够以较低的 功率消耗满足不同用户的 SINR 要求，更好的适用于信道频繁切换，功耗要求低的认知无线 电系统。 关键词：通信与信息系统；博弈论；认知无线电；功率控制 中图分类号：TN929.5 A Power Control Algorithm with fast Convergence based on Game theory YUAN Jide, ZHAO Danfeng (College of Information and Communication Engineeri, Harbin Engineering University, Harbin 150001) Abstract: Aiming at the discrepancies of the requirement among the different users in Cognitive Radios, a novel Nash game algorithm for power control was proposed which can be applied in code division multiple access (CDMA) system. The uniqueness and existence of the Nash Equilibrium was proved for the scheme. Simulations show that the algorithm can effectively restrain the mutual interference with fast convergence, and meet the different signal to interference plus noise ratio (SINR) requirement with low power. Key words: communication and information systems; game theory; cognitive radio; power control 0 引言 10 15 20 25 认知无线电是一种智能的无线通信技术，它能够不断地感知周围的通信环境，通过对环 境信息的分析判断，利用其自身系统的自适应性调整内部参数以适应环境变化，其关键技术 包括频谱分配、功率控制等。认知无线电中的功率控制技术能够很大程度上减少系统中用户 能量的消耗并抵抗他用户带来的干扰。 30 目前，基于博弈论的功率控制算法是认知无线电领域中的研究热点，主要方向集中在网 络收敛特性及环境认知方面。文献[1]提出的经典功率算法，但不具备根据环境变化调整自身 信干比的能力， 存在功率浪费的问题；在此基础上，Koskie-Gajic 提出了一种基于信干比 (SINR)的功率控制博弈算法[2]，但是该系统的部分用户由于其信干比最终收敛值低于信干比 阈值要求，而导致通信阻塞；文献[3]提出的 CR-APCG 算法引入自适应参数，加快了收敛速 度，但是伴随着发射功率迅速增加的问题。本文提出一种基于信干比的认知无线电自适应功 率控制博弈算法。该算法可根据认知用户的信干比阈值自适应调整发射功率，并具备更快的 收敛速度，实现各用户共享频谱资源的目的。 1 系统模型 基金项目：中央高校基本科研业务专项基金（HEUCF130802）。 作者简介：袁骥德（1988），男，硕士，主要研究方向：卫星通信，功率控制 通信联系人：赵旦峰（1965），男，教授，主要研究方向：高效编码及通信技术， 现代通信系统. E-mail: zhaodanfeng@hrbeu.edu.cn 35 40 - 1 -
    中国科技论文在线 http://www.paper.edu.cn 为不失一般性，本文采用的仿真模型为单小区 CDMA 认知无线电系统，用户随机分布 在 的小区内，基站位于小区中心， 为基站与用户 的距离，则用户 的信干比可 表示为 (1) 45 其中，信道增益模型 采用 ， 、 为常数。 为背景噪声功率， 表示第 个 用户的发射功率， 表示认知用户 和认知用户 信号的互相关系数。 为用户认 知用户 受到的系统总干扰。若设用户 的目标信干比阈值是 ，则该用户的输出信干比应 有 ， 。 2 算法模型 50 令 认知无线电系统中，每个用户追求最大化受益，可以将其表述为非合作博弈功率控制[4]。 为认知无线电功率控制博弈空间[5]。其中 表示 用户数集合； 表示认知用户发射功率集合； 表示第 个用 户的代价函数。根据纳什均衡理论，非合作功率控制的纳什均衡解会使得任何用户都不能单 方面改变其状态而获得额外收益[2]。即存在第 个用户的发射功率和输出 SIR 满足 55 (2) 本文提出的代价函数为 (3) 其中， 为认知用户 的信干比， 为满足用户最低通信要求的 SIR 阈值； 为 SIR 上限限制因子，当用户信干比 时，则将通过算法 限制用户信干比，既保 60 证该用户的信干比满足通信需求，又尽可能降低其的发射功率。 为目标信干比，并且 。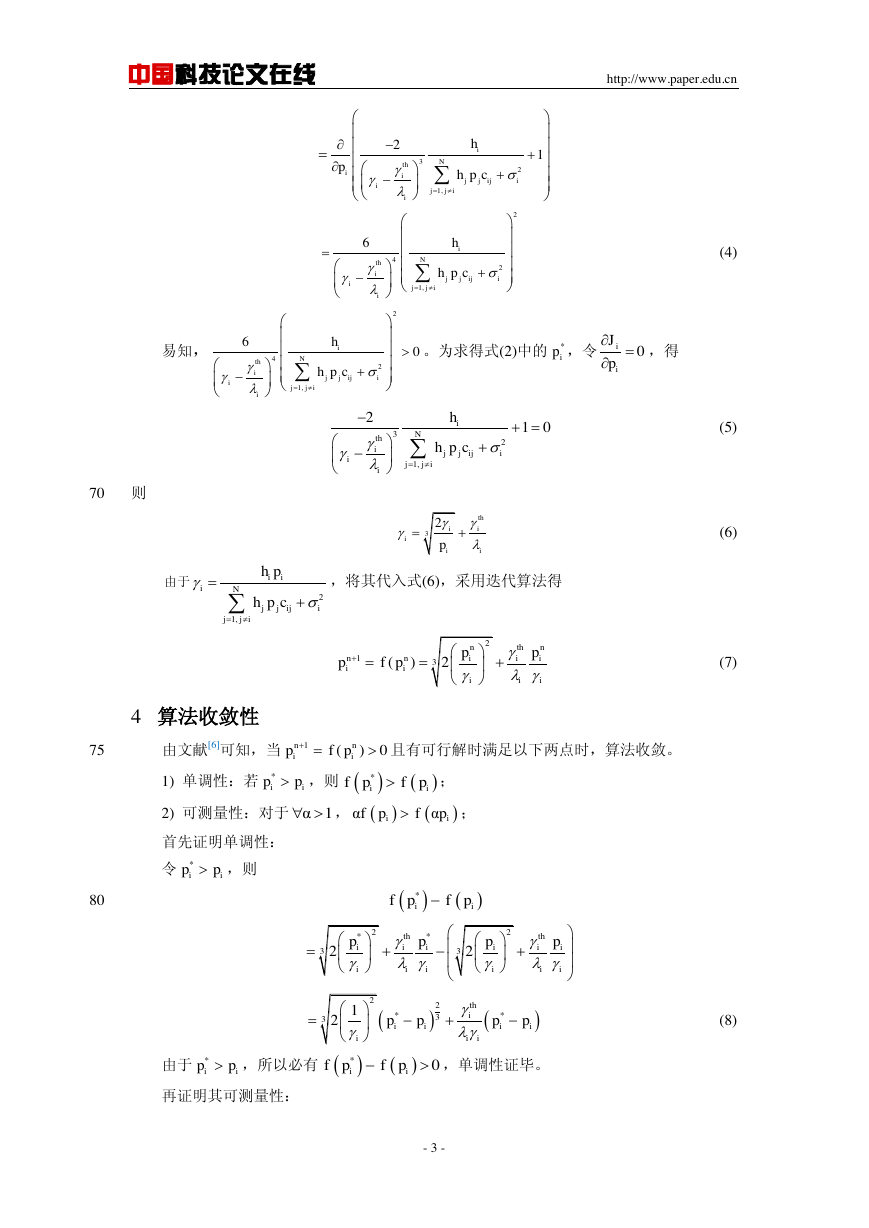 3 算法迭代公式推导 根据博弈论相关理论可知，代价函数 必须为关于功率 的凸函数，才能 存在最小值。为证明代价函数是凸函数，对代价函数求关于功率 的二阶导数，可得 65 - 2 - 233kmidii21,iiiiNjijjjihphpcih/iihAdA2ipiijcij1,Njjijjjihpciithithiii[,,{(,())}]iiiMJpgpNp{1,2,,}NN12{,,,}TNpppp,iiiiJppii**,iiiJpp*****121,,,,,,iiiiiNJpppppp1,2,,ipiN，21,/iiiiithiiiJpppiithiitariiiiitaritaritarthii,iiiiJppipip22,iiiiiJppp
    中国科技论文在线 http://www.paper.edu.cn (4) 易知， 。为求得式(2)中的 ，令 ，得 70 则 (5) (6) 由于 ，将其代入式(6)，采用迭代算法得 4 算法收敛性 75 由文献[6]可知，当 且有可行解时满足以下两点时，算法收敛。 (7) 1) 单调性：若 ，则 2) 可测量性：对于 ， ； ； 首先证明单调性： 令 ，则 80 (8) 由于 ，所以必有 ，单调性证毕。 再证明其可测量性： - 3 - 321,21iNthiijjijiijjiihphpc2421,6iNthijjijiijjiihhpc2421,60iNthijjijiijjiihhpc*ip0iiJp321,210iNthijjijiijjiihhpc32thiiiiip21,iiiNjjijijjihphpc213()2nthnnniiiiiiiipppfp1()0nniipfp*iipp*iifpfpα1ααiifpfp*iipp*iifpfp22**3322ththiiiiiiiiiiiipppp22**3312thiiiiiiiipppp*iipp*0iifpfp
    中国科技论文在线 http://www.paper.edu.cn 85 (9) 式中 ，所以 ，故 。 综上可知，算法收敛于一点。 90 5 Nash 均衡解的存在性和唯一性 为证明算法的 Nash 均衡解存在且收敛一点，使 ，则有 令函数 (10) 95 (11) 由隐函数理论[6]知，当式(11)的雅可比矩阵非奇异时存在纳什均衡解，则有 其中， (12) (13) 100 为一常数，故式(13)中主对角线等于-1，其他各元素的取值由 确定。在 CDMA 通信系统 中，扩频码 互相关系数通常都很小，因此雅可比行列式的值主要由主对角线值决定，此 时行列式不为 0，故迭代式的雅可比矩阵非奇异。因此本算法存在唯一的纳什均衡解。 - 4 - ααiifpfp2233ααα22ththiiiiiiiiiiiipppp2233αα2iipα123αααα0iifpfp,0iiiiiiJpppp221,302Njjijijjiiihpcph21,Njjijithjjiiiihpch2,,a,,,,iiiiiijiFpphc221,32Njjijijjiiihpcph21,Njjijithjjiiiihpch1112122221221,,a,,,,NiiiiiijiNiNNNNFFFpppFFFFpphcppppFFFpppijFp123·1thjjijijijjijiiiiihpchchckijhjhihkijcijc
    中国科技论文在线 6 算法仿真和性能分析 http://www.paper.edu.cn 仿真采用相同的噪声环境，噪声功率为 6×10-13mW。扩频码长度为 256，故 。 105 信道增益模型为 ，其中 10-11，α=4。认知用户的初始发射功率为 10-16mW，信干 比阈值设为 =7dB，目标信干比设为 =9dB。 图 1 用户输出信干比比较 图 2 用户发射功率比较 Fig. 1 Performance comparison of output SINR Fig. 2 Performance comparison of transmission 110 among four algorithm power among four algorithms 用户将随机分布在小区内以保证仿真不失一般性。图 1 所示为经典功率控制算法， 115 Koskie-Gajic 算法，CR-APCG 算法以及本文算法随迭代次数的增加 25 个认知用户的输出信 干比。经典功率控制算法使系统中不同的认知用户在一定的迭代次数后趋于目标信干比，但 是以浪费发射功率为代价；Koskie-Gajic 算法中，部分用户随着迭代次数的增加信干比逐渐 下降，出现低于信干比阈值的现象，无法满足通信需求；CR-APCG 算法信干比上升很快， 部分用户的信干比超过 后迅速调整回目标信干比，但认知用户的信干比收敛值均在较 120 高，系统发射功率仍存在一定浪费；本文中的算法在满足所有认知用户信干比高于信干比阈 值的前提下，使更多的用户信干比收敛在较低位置，在不影响通话质量的同时进一步降低系 统功耗。 图 2 为 25 个认知用户下，用户发射功率随 4 种算法迭代次数增加的比较。Koskie-Gajic 算法中用户的发射功率较经典功率控制算法的差别不明显；而 CR-APCG 算法中的用户在发 125 射功率收敛后，较多用户收敛在较低的功率，但是整体功率仍然较高；本文算法的中，认知 用户整体发射功率都得到了有效控制，在满足 SIR 需求的同时，相较其他算法总体发射功率 优势明显。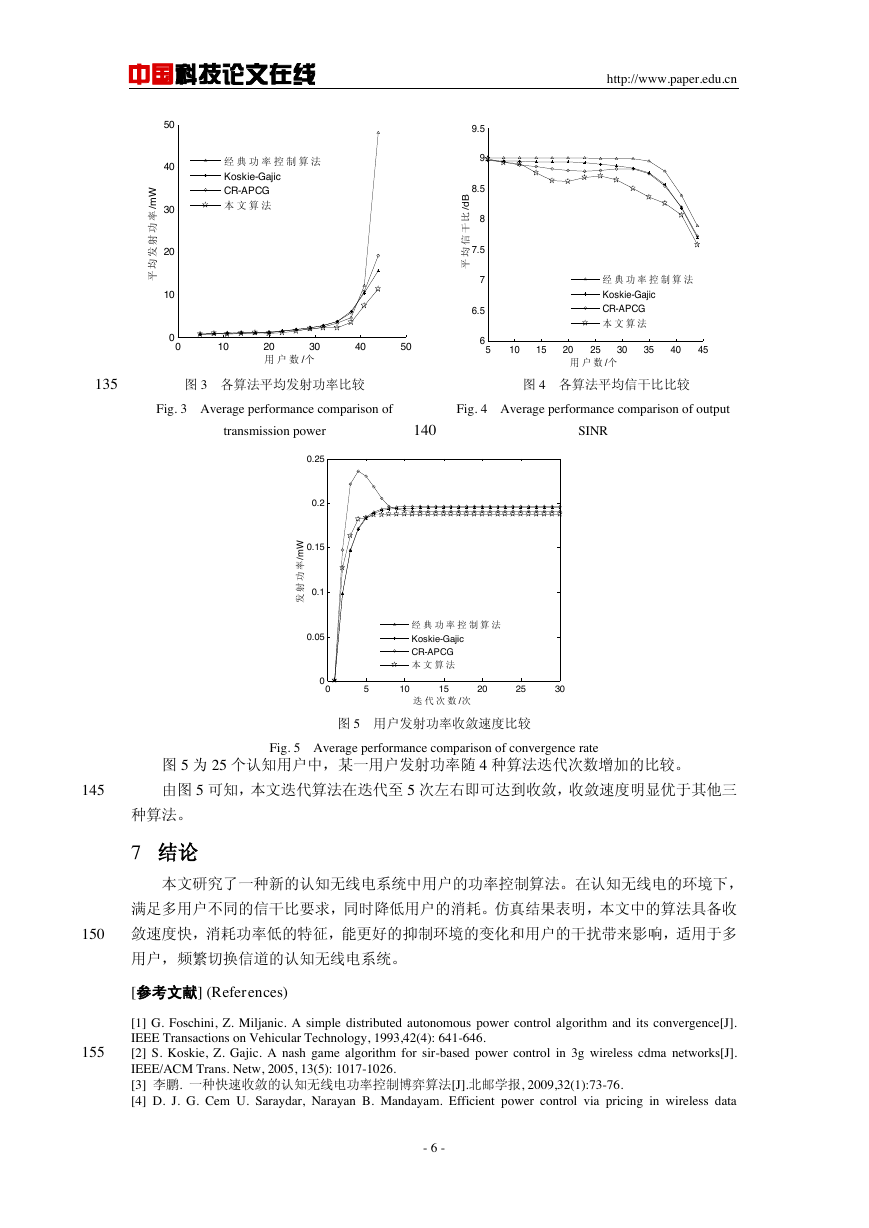 图 3 和图 4 分别为 4 种算法随用户数目改变的平均发射功率和平均信干比比较图。 从图 3 中的对比曲线中可知，在用户数较少的情况下，各种算法的平均发射功率差别不 130 大，当用户数高于 30 后，各算法下的发射功率开始不同。本文中的算法在用户数增多后仍 然能低于其他 3 种算法。同时结合图 4 可知，平均发射功率较低的原因在于本文中的控制算 法使得平均信干比收敛在较低位置，并且能够保证其信干比仍高于预设指标，满足通信要求， 实现了对不同认知用户的有效控制。 - 5 - 1256ijciiAhrAthitari01020300510迭代次数/次信干比/dB(a) 经典功率控制算法01020300510迭代次数/次信干比/dB(b) Koskie-Gajic 算法01020300510迭代次数/次信干比/dB(c) CR-APCG 算法01020300510迭代次数/次信干比/dB(d) 本文算法010203001234迭代次数/次发射功率/mW(a) 经典功率控制算法010203001234迭代次数/次发射功率/mW(b) Koskie-Gajic 算法01020300246迭代次数/次发射功率/mW(c) CR-APCG 算法01020300123迭代次数/次发射功率/mW(d) 本文算法tari
    中国科技论文在线 http://www.paper.edu.cn 135 图 3 各算法平均发射功率比较 图 4 各算法平均信干比比较 Fig. 3 Average performance comparison of Fig. 4 Average performance comparison of output transmission power 140 SINR 图 5 用户发射功率收敛速度比较 图 5 为 25 个认知用户中，某一用户发射功率随 4 种算法迭代次数增加的比较。 Fig. 5 Average performance comparison of convergence rate 145 由图 5 可知，本文迭代算法在迭代至 5 次左右即可达到收敛，收敛速度明显优于其他三 种算法。 7 结论 本文研究了一种新的认知无线电系统中用户的功率控制算法。在认知无线电的环境下， 满足多用户不同的信干比要求，同时降低用户的消耗。仿真结果表明，本文中的算法具备收 150 敛速度快，消耗功率低的特征，能更好的抑制环境的变化和用户的干扰带来影响，适用于多 用户，频繁切换信道的认知无线电系统。 [参考文献] (References) 155 [1] G. Foschini, Z. Miljanic. A simple distributed autonomous power control algorithm and its convergence[J]. IEEE Transactions on Vehicular Technology, 1993,42(4): 641-646. [2] S. Koskie, Z. Gajic. A nash game algorithm for sir-based power control in 3g wireless cdma networks[J]. IEEE/ACM Trans. Netw, 2005, 13(5): 1017-1026. [3] 李鹏. 一种快速收敛的认知无线电功率控制博弈算法[J].北邮学报, 2009,32(1):73-76. [4] D. J. G. Cem U. Saraydar, Narayan B. Mandayam. Efficient power control via pricing in wireless data - 6 - 0102030405001020304050用户数/个平均发射功率/mW 经典功率控制算法Koskie-GajicCR-APCG本文算法5101520253035404566.577.588.599.5用户数/个平均信干比/dB 经典功率控制算法Koskie-GajicCR-APCG本文算法05101520253000.050.10.150.20.25迭代次数/次发射功率/mW 经典功率控制算法Koskie-GajicCR-APCG本文算法
    中国科技论文在线 http://www.paper.edu.cn 160 networks[J]. IEEE Transations on Communications, 2002, 50(2): 291-303. [5] C. T. A. M. Hayajneh. Distributed joint rate and power control gametheoretic algorithms for wireless data[J]. IEEE Communication Letters, 2004, 8(8): 511-513. [6] R. Yates. A framework for uplink power control in cellular radio systems[J]. IEEE Journal on Selected Areas in Communications, 1995, 13(7): 1341–1347. - 7 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料