2014，50（3）1引言传统的特征提取方法主要包括时域上的波形结构特征提取、频域上的经典谱估计、现代谱估计和高阶谱估计特征提取以及时间-频率域上的短时傅里叶变换、小波变换等方法。由于水声信号的非线性和非平稳性，从中提取出可以反映目标特性的有效特征一直是这个领域的难题，传统的特征提取方法在处理此类问题时具有一定的局限性。如傅里叶变换分析方法在任一频点上的值是整个时间轴上的积分平均，因此不能很好地反映非平稳信号的时变特征。小波分析虽然能同时提供信号的时域和频域的局部化信息，但由于小波基函数长度有限，在对信号作小波变换时会产生能量泄露[1]，因而难以对信号作精准的时频域分析。经验模态分解（EMD）是由HuangNE在1998年提出的Hilbert-Huang变换中的信号处理算法，该方法在对非平稳时变信号进行多尺度分解时相对于传统的小基于IMF能量谱的水声信号特征提取与分类刘深，张小蓟，牛奕龙，汪平平LIUShen,ZHANGXiaoji,NIUYilong,WANGPingping西北工业大学航海学院，西安710072SchoolofMarineEngineering,NorthwesternPolytechnicUniversity,Xi’an710072,ChinaLIUShen,ZHANGXiaoji,NIUYilong,etal.FeatureextractionandclassificationexperimentofunderwateracousticsignalsbasedonenergyspectrumofIMF’s.ComputerEngineeringandApplications,2014,50（3）：203-206.Abstract：EmpiricalModeDecomposition（EMD）isamethodofsignalanalysisforprocessingnonlinearandnon-sta-tionarysignal.EMDcandecomposeoutdifferenttimescaleoflocalfeaturefromtheoriginalsignal.AndthentheIntrinsicModeFunction（IMF）ofthoselocalcharacteristicsignalsisgot.Anewfeatureextractionandselectionmethodofunder-wateracousticsignalsbasedonenergyspectrumofIntrinsicModeFunction（IMF’s）ispresented,wheretheseintrinsicmodecomponentsaredecomposedviaempiricalmodedecompositionfromoriginalsignalsandtransformedintoenergyspectrumfeaturevectors,andthusthedifferentsignals’energyspectrumfeaturesofsub-bandfrequencycanbeinspected.SupportVectorMachine（SVM）classifierisusedforclassificationexperiments.Theresultsshowthatthecorrectidentifi-cationratioofexperimentsbasedonIMF’senergyspectrumisabove88%,whichissuperiortofeatureextractionofwaveletenergyspectrum.Keywords：EmpiricalModeDecomposition（EMD）;IntrinsicModeFunction（IMF）;IntrinsicModeFunction（IMF）energyspectrum;featureextraction;SupportVectorMachine（SVM）classifier摘要：经验模态分解（EMD）是用来处理非平稳时变信号的一种信号分析方法，该方法对所分析信号的局部特征信号进行不同时间尺度的分解，从而得到这些局部特征信号的各阶本征模函数（IMF）。提出了一种基于IMF能量谱的水声信号特征提取与选择方法，通过对水声信号进行经验模态分解，提取信号的本征模式分量并转换为能量谱特征向量，从而观测不同信号子频带能量谱的特征变化。分类实验采用支持向量机（SVM）分类器进行。实验结果表明，相对于小波能量谱特征提取法而言，利用IMF能量谱作为特征向量的分类实验具有更佳的分类效果，平均正确率达88%以上。关键词：经验模态分解；本征模函数；本征模函数能量谱；特征提取；支持向量机（SVM）分类器文献标志码：A中图分类号：TN911.7doi：10.3778/j.issn.1002-8331.1207-0213基金项目：西北工业大学基础研究基金（No.JC201108）。作者简介：刘深（1988—），男，硕士研究生，主要研究方向为信号检测与处理技术；张小蓟（1958—），男，副教授，主要研究方向为信号检测与处理技术；牛奕龙（1979—），男，副教授，主要研究方向为信号处理与人工智能；汪平平（1988—），女，硕士研究生，主要研究方向为通信信号检测与处理技术。E-mail：npuliushen@gmail.com收稿日期：2012-07-16修回日期：2012-09-24文章编号：1002-8331（2014）03-0203-04CNKI网络优先出版：2012-10-11，http://www.cnki.net/kcms/detail/11.2127.TP.20121011.1017.017.htmlComputerEngineeringandApplications计算机工程与应用203

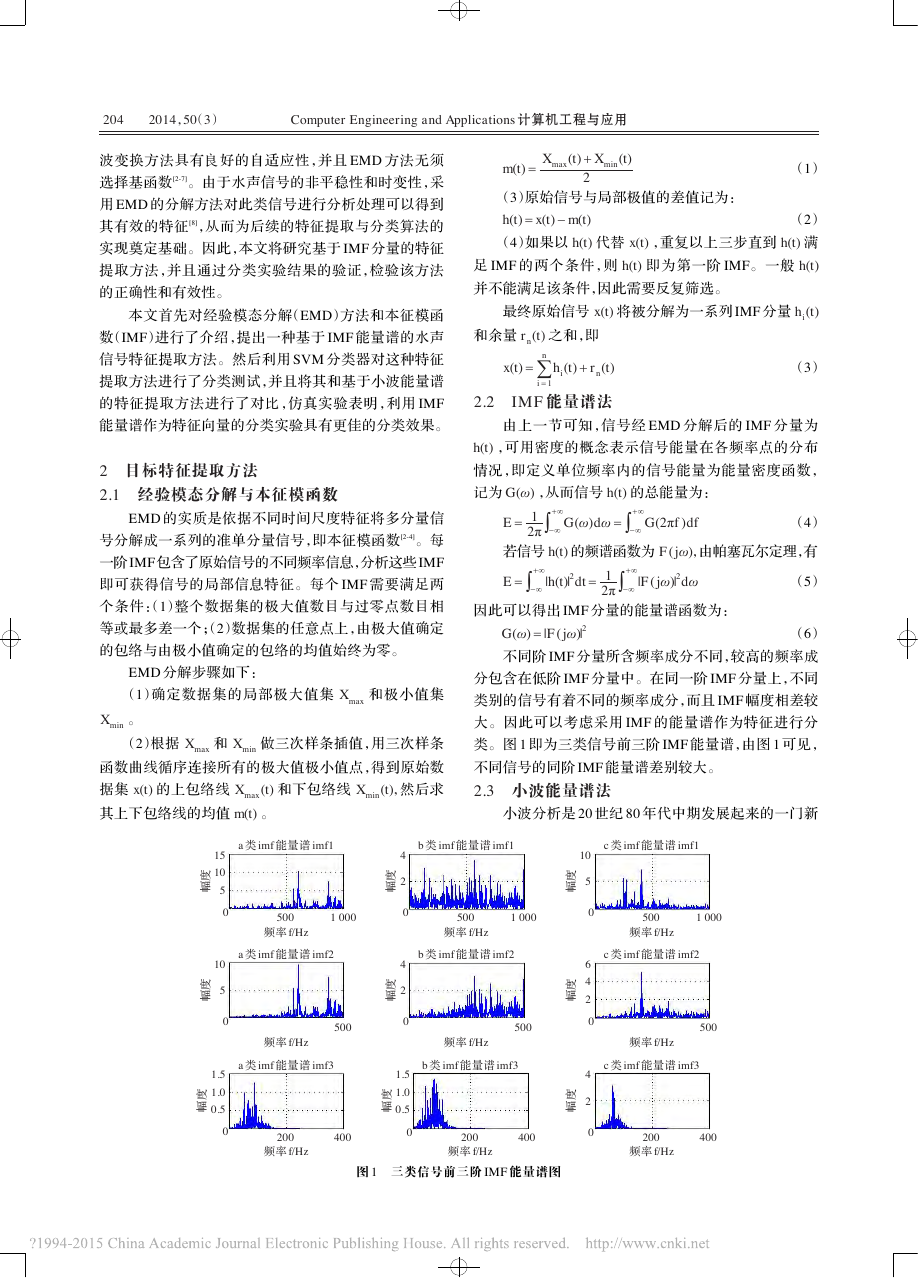
ComputerEngineeringandApplications计算机工程与应用2014，50（3）波变换方法具有良好的自适应性，并且EMD方法无须选择基函数[2-7]。由于水声信号的非平稳性和时变性，采用EMD的分解方法对此类信号进行分析处理可以得到其有效的特征[8]，从而为后续的特征提取与分类算法的实现奠定基础。因此，本文将研究基于IMF分量的特征提取方法，并且通过分类实验结果的验证，检验该方法的正确性和有效性。本文首先对经验模态分解（EMD）方法和本征模函数（IMF）进行了介绍，提出一种基于IMF能量谱的水声信号特征提取方法。然后利用SVM分类器对这种特征提取方法进行了分类测试，并且将其和基于小波能量谱的特征提取方法进行了对比，仿真实验表明，利用IMF能量谱作为特征向量的分类实验具有更佳的分类效果。2目标特征提取方法2.1经验模态分解与本征模函数EMD的实质是依据不同时间尺度特征将多分量信号分解成一系列的准单分量信号，即本征模函数[2-4]。每一阶IMF包含了原始信号的不同频率信息，分析这些IMF即可获得信号的局部信息特征。每个IMF需要满足两个条件：（1）整个数据集的极大值数目与过零点数目相等或最多差一个；（2）数据集的任意点上，由极大值确定的包络与由极小值确定的包络的均值始终为零。EMD分解步骤如下：（1）确定数据集的局部极大值集Xmax和极小值集Xmin。（2）根据Xmax和Xmin做三次样条插值，用三次样条函数曲线循序连接所有的极大值极小值点，得到原始数据集x(t)的上包络线Xmax(t)和下包络线Xmin(t)，然后求其上下包络线的均值m(t)。m(t)=Xmax(t)+Xmin(t)2（1）（3）原始信号与局部极值的差值记为：h(t)=x(t)-m(t)（2）（4）如果以h(t)代替x(t)，重复以上三步直到h(t)满足IMF的两个条件，则h(t)即为第一阶IMF。一般h(t)并不能满足该条件，因此需要反复筛选。最终原始信号x(t)将被分解为一系列IMF分量hi(t)和余量rn(t)之和，即x(t)=åi=1nhi(t)+rn(t)（3）2.2IMF能量谱法由上一节可知，信号经EMD分解后的IMF分量为h(t)，可用密度的概念表示信号能量在各频率点的分布情况，即定义单位频率内的信号能量为能量密度函数，记为G(ω)，从而信号h(t)的总能量为：E=12π-¥+¥G(ω)dω=-¥+¥G(2πf)df（4）若信号h(t)的频谱函数为F(jω)，由帕塞瓦尔定理，有E=-¥+¥|h(t)|2dt=12π-¥+¥|F(jω)|2dω（5）因此可以得出IMF分量的能量谱函数为：G(ω)=|F(jω)|2（6）不同阶IMF分量所含频率成分不同，较高的频率成分包含在低阶IMF分量中。在同一阶IMF分量上，不同类别的信号有着不同的频率成分，而且IMF幅度相差较大。因此可以考虑采用IMF的能量谱作为特征进行分类。图1即为三类信号前三阶IMF能量谱，由图1可见，不同信号的同阶IMF能量谱差别较大。2.3小波能量谱法小波分析是20世纪80年代中期发展起来的一门新200400频率f/Hz1.51.00.5幅度a类imf能量谱imf30200400频率f/Hz幅度1.51.00.5b类imf能量谱imf30200400频率f/Hz42幅度c类imf能量谱imf30151055001000幅度频率f/Hza类imf能量谱imf105001000频率f/Hz42幅度b类imf能量谱imf105001000频率f/Hz105幅度c类imf能量谱imf10500频率f/Hz105幅度a类imf能量谱imf20500频率f/Hz42幅度b类imf能量谱imf20500频率f/Hz642幅度c类imf能量谱imf20图1三类信号前三阶IMF能量谱图204

2014，50（3）兴的数学理论和方法，通过小波变换可以将研究对象分解到不同尺度的空间进行分析和处理[9-10]。任一能量有限函数f(t)ÎL2(R)关于小波函数g(t)的连续小波变换为：Wgf(sτ)=1sf(t)g*(t-τs)dt（7）式中，s，τ均为连续变量，s是尺度因子，*表示共轭。小波函数g(t)必须满足容许条件：cg=-¥+¥|G(ω)|2ωdω<¥（8）式中，G(ω)是g(t)的傅里叶变换。定义信号在(sτ)平面上的能量密度函数为：E(sτ)=|Wgf(sτ)|2cgs2（9）本文使用的小波基函数为Daubechies，使用Db3对三类信号分别进行五层分解，选取前三层低频小波系数进行特征提取实验。图2即为三类信号小波系数能量谱图。3分类实验基于IMF能量谱的特征提取及分类过程如图3所示。输入信号首先进行预处理，如归一化，去直流分量等。然后对信号进行经验模态分解，得到各阶IMF分量。求出IMF能量谱，从中选择合适的特征向量作为分类器的输入。最后得到分类结果。本文进行分类实验所使用的a，b，c三类信号为水下不同背景的噪声信号。每类信号有60个样本，每个样本数据长度为500。对这60个样本分别进行N=9的经验模态分解，利用式（6）求其IMF能量谱，然后求出其能量谱谱峰值的均值。对于EMD分解来说，前三层分解结果已经包含原始信号90%的能量，基本可以代表原始信号的主要特征。故本文只选用EMD的前三阶分解结果用于实验。经过以上过程，从60个样本数据中可以提取出一个3×60的特征矩阵，即实验所需的60组3维特征向量。从这60组维数为3的特征向量中抽取15组作为分类器训练集，再从剩余的45组中随机抽取25组作为测试集，利用SVM分类器对其进行分类实验，其中核函数为径向基（RBF）函数，分类器惩罚参数取c=1，核函数参数取g=0.01。使用小波系数能量谱特征提取法数据处理方法与之类似，最后也可得出60组维数为3的特征向量。从这60组特征中抽取15组作为分类器训练集，剩下45组中随机抽取25组作为测试集。图4和图5分别为将第20组样本利用不同特征提取法得出的能量谱图，将该数据按照上述数据处理过程进行均值处理后得出其特征向量如表1和表2所示。由表1和表2对比可以看出，利用IMF能量谱提取法所得出的不同信号的特征向量之间间距更大，由于本2004000频率f/Hz2010幅度第三层b类2004005幅度0频率f/Hz第三层a类2004000频率f/Hz2010幅度第三层c类5000频率f/Hz2010幅度第二层c类50042幅度0频率f/Hz第二层a类5000频率f/Hz2010幅度第二层b类500100042幅度0频率f/Hz第一层a类50010002010幅度0频率f/Hz第一层b类50010002010幅度0频率f/Hz第一层c类图2三类信号低频前三层小波能量谱图图3基于IMF能量谱的特征提取及分类过程信号预处理EMDIMF分量能量谱计算特征向量选择分类器分类结果a类0.31700.31510.1520b类1.81580.51510.2533c类0.46340.46180.1711表1IMF能量谱法部分特征向量a类0.34970.39000.3778b类0.67480.67420.4597c类0.48600.47180.4574表2小波能量谱法部分特征向量刘深，张小蓟，牛奕龙，等：基于IMF能量谱的水声信号特征提取与分类205

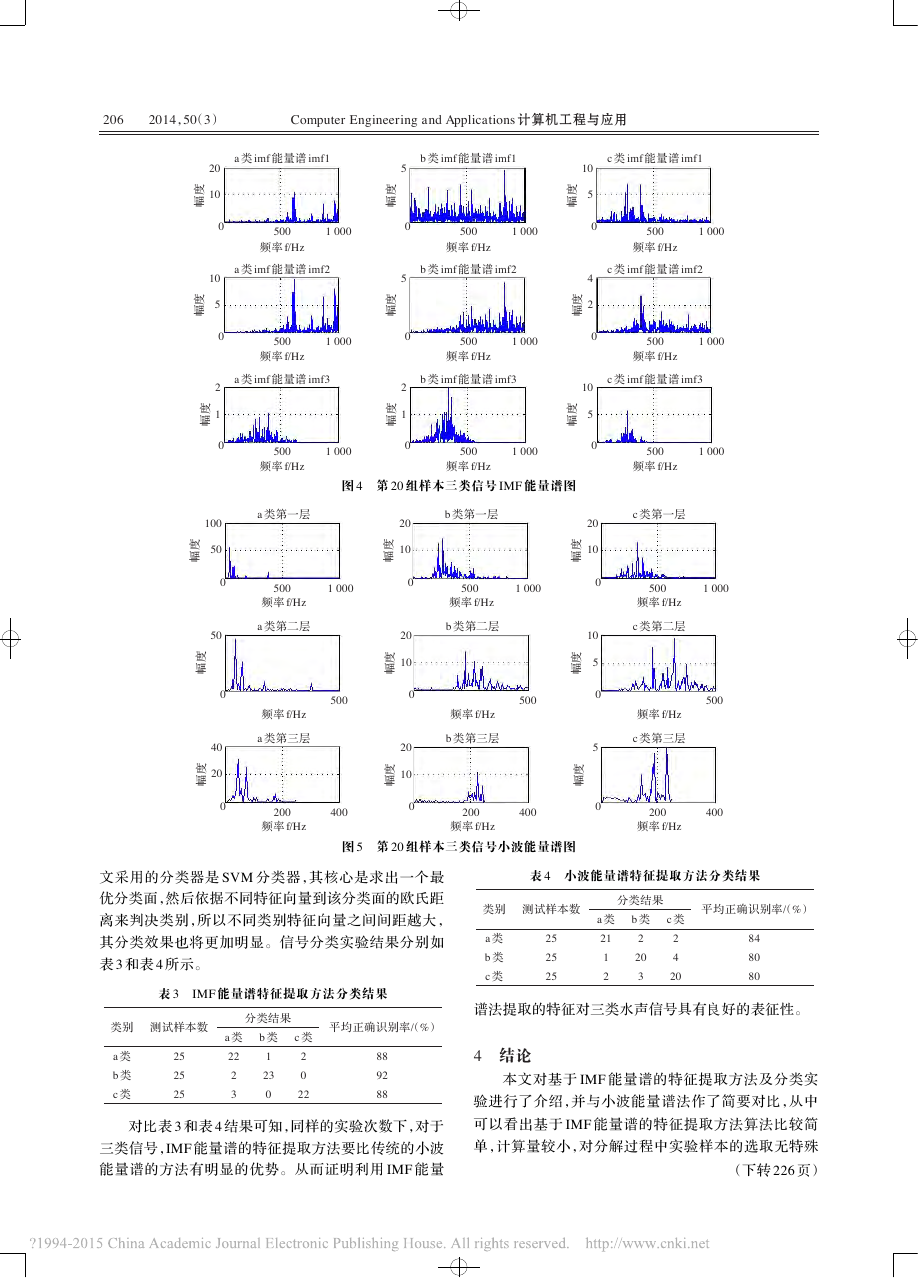
ComputerEngineeringandApplications计算机工程与应用2014，50（3）文采用的分类器是SVM分类器，其核心是求出一个最优分类面，然后依据不同特征向量到该分类面的欧氏距离来判决类别，所以不同类别特征向量之间间距越大，其分类效果也将更加明显。信号分类实验结果分别如表3和表4所示。对比表3和表4结果可知，同样的实验次数下，对于三类信号，IMF能量谱的特征提取方法要比传统的小波能量谱的方法有明显的优势。从而证明利用IMF能量谱法提取的特征对三类水声信号具有良好的表征性。4结论本文对基于IMF能量谱的特征提取方法及分类实验进行了介绍，并与小波能量谱法作了简要对比，从中可以看出基于IMF能量谱的特征提取方法算法比较简单，计算量较小，对分解过程中实验样本的选取无特殊图5第20组样本三类信号小波能量谱图100505001000频率f/Hz0幅度a类第一层20105001000频率f/Hz0幅度b类第一层5001000频率f/Hz0c类第一层2010幅度500频率f/Hz0c类第二层105幅度500频率f/Hz0幅度a类第二层50500频率f/Hz0b类第二层2010幅度200400频率f/Hz0b类第三层2010幅度4020200400频率f/Hz0a类第三层200400频率f/Hz0c类第三层5幅度幅度5001000频率f/Hz21幅度0a类imf能量谱imf35001000频率f/Hz105幅度0c类imf能量谱imf35001000频率f/Hz21幅度0b类imf能量谱imf35001000频率f/Hz2010幅度0a类imf能量谱imf15001000频率f/Hz105幅度0c类imf能量谱imf15001000频率f/Hz5幅度0b类imf能量谱imf15001000频率f/Hz105幅度0a类imf能量谱imf25001000频率f/Hz42幅度0c类imf能量谱imf25001000频率f/Hz05幅度b类imf能量谱imf2图4第20组样本三类信号IMF能量谱图类别a类b类c类测试样本数252525a类2223b类1230c类2022平均正确识别率/（%）889288分类结果表3IMF能量谱特征提取方法分类结果类别a类b类c类测试样本数252525a类2112b类2203c类2420平均正确识别率/（%）848080分类结果表4小波能量谱特征提取方法分类结果（下转226页）206

ComputerEngineeringandApplications计算机工程与应用2014，50（3）[6]BauerDF，TubbsRS，Acakpo-SatchiviL.Mycoplasmameningitisresultinginincreasedproductionofcerebro-spinalfluid：casereportandreviewoftheliterature[J].ChildsNervSyst，2008，24：859-862.[7]俞增仙，董春富.脑脊液6项指标检测对脑膜炎的诊断价值[J].中华医院感染学杂志，2010，20（9）：1339-1340.[8]胡佳，张家堂，郎森阳，等.结核性脑膜炎167例脑脊液分析[J].解放军医学杂志，2010，35（5）：580-583.[9]JoSH，ChangT，EbongI，etal.Nanoscalememristordeviceassynapseinneuromorphicsystems[J].NanoLett，2010，10（4）：1297-1301.[10]PershinYV，VentraMD.Experimentaldemonstrationofasso-ciativememorywithmemristiveneuralnetworks[J].NeuralNetworks，2010，23（7）：881-886.[11]ItohM，ChuaLO.Memristorcellularautomataandmem-ristordiscrete-timecellularneuralnetworks[J].IntJBifur-cationChaos，2009，19（11）：3605-3656.[12]BiolekZ，BiolekD，BiolkovaV.SPICEmodelofmem-ristorwithnonlineardopantdrift[J].RadioEng，2009，18（2）：210-214.[13]BatasD，FiedlerH.AmemristorSPICEimplementationandanewapproachformagneticflux-controlledmem-ristormodeling[J].IEEETransonNanotechnol，2011，10（2）：250-255.[14]ShinS，KimK，KangSM.Compactmodelsformem-ristorsbasedoncharge-fluxconstitutiverelationships[J].IEEETransonCADIntCircSyst，2010，29（4）：590-598.[15]StrukovDB，BorghettiJL，WilliamsRS.Coupledionicandelectronictransportmodelofthin-filmsemiconductormemristivebehavior[J].Small，2009，5（9）：1058-1063.[16]RamosCZ，MesaLAC，CarrascoJAP，etal.Onspike-timing-dependent-plasticity，memristivedevices，andbuildingaself-learningvisualcortex[J].FrontiersNeurosci，2011，5.[17]潘长波，李红星.反馈神经网络用于多输入输出动态系统建模[J].计算机应用，2009，29（6）：335-336.[18]朱凯，王正林.精通MATLAB神经网络[M].北京：电子工业出版社，2010.[19]程绪超，陈新宇，郭平.基于改进Elman网络模型的软件可靠性预测[J].通信学报，2011，32（4）：86-93.[20]乔琛.局部域反馈神经网络的全局收敛性[J].应用数学学报，2009，32（3）：536-545.[21]史忠植.神经网络[M].北京：高等教育出版社，2009.（上接206页）要求，实验中的训练样本和测试样本都是随机抽取的，从分类实验的结果来看，该方法对水声信号分类具有良好的识别分类效果。参考文献：[1]石春香，罗奇峰.时程信号的Hilbert-Huang变换与小波分析[J].地震学报，2003，25（4）：398-405.[2]HuangNE.TheEmpiricalModeDecompositionandHil-bertspectrumfornonlinearandnon-stationarytimeseriesanalysis[J].ProcRSoc，1998，454（12）：903-995.[3]张小蓟，张歆，孙进才.基于经验模态分解的目标特征提取与选择[J].西北工业大学学报，2006，26（4）：453-456.[4]刘文海，李关防.经验模态分解在直升机谱特征提取中的应用[J].哈尔滨工程大学学报，2010，31（6）：714-719.[5]JiangJinshui.Researchonthemethodoffeaturesextrac-tionfornon-stationarytransientsignal[C]//CommunicationSoftwareandNetworks，2009：637-641.[6]SunZhaowei，ShiGang，LiuXiaoping.StructuraldamageidentificationmethodbasedonIMFmodelenergyfeatureandBPneuralnetwork[C]//IntelligenceScienceandInfor-mationEngineering（ISIE），2011：206-209.[7]JiaoWeidong.Amethodfortime-frequencyfeatureextrac-tionfromvibrationsignalbasedonHilbert-HuangTrans-form[C]//IntelligentControlandAutomation，2008：8460-8464.[8]张小蓟，张歆，孙进才.基于IMF能量熵的目标特征提取与分类方法[J].计算机工程与应用，2008，44（4）：68-69.[9]刘建国，李志舜.基于连续小波变换的湖底回波特征提取[J].西北工业大学学报，2006，24（1）：111-114.[10]张静远，张冰，蒋兴舟.基于小波变换的特征提取方法分析[J].信号处理，2006，16（2）：156-158.[11]吕艳新，孙书学，顾晓辉.基于EMD和能量比的战场声目标分类与识别[J].振动与冲击，2008，27（11）：51-55.[12]赵志宏，杨绍普.基于相对小波能量的滚动轴承故障诊断[J].电子测量与仪器学报，2011，25（1）：44-49.226