第1页 / 共20页
第2页 / 共20页
第3页 / 共20页
第4页 / 共20页
第5页 / 共20页
第6页 / 共20页
第7页 / 共20页
第8页 / 共20页
基于TD-SCDMA系统的频偏估计算法研究.pdf
http://www.paper.edu.cn
基于 TD-SCDMA 系统的频偏估计算法研究1
范欣然 1，彭涛 2，王文博 3
1 北京邮电大学信息与通信工程学院，北京(100876)
E-mail：xinran.fan@gmail.com
摘 要： 本文从原理上推导了四种经典的误差估计算法——Kay、Fitz、L&R 以及 Kay&R
算法，通过分析、比较和多方面仿真验证了多种因素对算法性能的影响，如性能评判标准、
待测参量之间的影响、观测序列长度的选取等等，并且这些参数对于频率误差估计影响是不
同的。同时从估计范围、估计精度和运算复杂度等方面对现有的 4 种频偏估计算法进行研究
和仿真，给出了算法的选择依据和详细的分析结果。在此基础上，研究了基于用户数据和训
练序列的联合频偏估计算法，分析了估计范围和运算复杂度，并采用迭代的方法进一步提高
了算法性能。希望这些理论依据对测试仪的误差估计算法起到指导和借鉴作用。
关键词：时分同步码分多址系统， 频偏估计， 性能分析，克拉美-劳下界
中图分类号：TN929.5
1. 引 言
在时分同步码分多址（TD-SCDMA）系统中，由于收发设备间的频率偏差和多普勒频
移，导致接收的基带信号存在一定的频偏，严重影响了信号的接收新能。因此，能否快速正
确地估计和校准频偏是正确接收数据的前提，是移动通信系统中必不可少的步骤[1]。
通常接收机采用锁相环来调整本地载波的频率，获得发送和接收数据之间的载波同步，
但 TD-SCDMA 的短突发通信体制不适合使用跟踪环。因此，本文立足于 TD-SCDMA 系统，
对频偏估计算法进行了详细分析与研究，选出了较好的实现方法来解决精确频偏估计的问
题。
2. TD-SCDMA 系统信号模型
m(t)
Reciprocal
m(t)
AWGN
Channel
r(t)
z(t)
Frequency
Offset
Estimator
图 2-1 系统链路模型
本文所参考的系统链路模型如图 2-1 所示，采用离散时间模型，采样周期等于系统的码
片间隔 cT 。图 2-2 给出了 TD-SCDMA 链路的时隙结构。一个时隙包含两个数据域和一个训
练序列，该训练序列将两个数据域分隔。在 TD-SCDMA 系统中，该训练序列称为 Midamble
1 本课题得到安捷伦公司资助。
- 1 -
序列。发送的训练序列为接收机所知，可以用来进行同步计算，本文利用该训练序列主要进
行频偏的估计。
http://www.paper.edu.cn
图 2-2
TD-SCDMA 系统链路的时隙结构
因此，传输的训练序列可以表示为：
( )
m t
=
j
π
i
(
δ
2
t
m e
i
−
iT
c
)
144
∑
i
1
=
信号 ( )m t 通过加性白高斯噪声信道后，得到的接受信号及其采样序列可以表示为：
( )
r t
=
e
j
(
)
ft
2
Δ +
π θ
j
π
i
(
δ
2
t
m e
i
−
iT
c
)
τ
−
+
( )
n t
144
∑
i
1
=
(2-1)
(2-2)
r
k
(
r kT
c
)
τ
e
(
f kT
2
Δ
π
c
j
⎡
⎣
)
⎤
+ +
τ θ
⎦
=
+
(2-3)
其中 fΔ 表示载波的频率偏移；θ是一个未知的随机相位偏移，其概率密度服从[
)
0,2π 的均
},k sn 是
匀分布；τ是时间偏移； ( )n t 是一个加性白高斯噪声，
相互独立的零均值高斯随机序列，方差都为 2 2σ 。由于训练序列为接收机所知，因此可以
},k cn 和{
，{
n
k c
,
n
k
jn
=
+
k s
,
+
m e
k
n
k
j
π
k
2
通过该训练序列获得有用信号。将 kr 与 (
的信号：
m kT
c
j
π
k
2
)
=
m e
k
相除生成输入载波频率偏移估计器
z
k
=
r
k
m e
k
j
π
k
2
2
Δ
π
(
f kT
c
j
⎡
⎣
)
⎤
+ +
τ θ
⎦
=
e
+
v k
,
k
=
N
1,2,
,
(2-4)
−
j
π
k
2
e
m
k
n
k
，{ }kv 为独立零均值高斯随
其中 N 为观测序列的长度，即为训练序列长度，
v
k
=
机序列。
3. 频偏估计算法介绍
3.1 Kay 算法
根据 Kay 算法[2]，将(2-4)转化为以下形式：
其中
x
k
v e
k
−
j
⎡
⎣
2
π
Δ
(
f kT
c
是：
z
=
k
)
⎤
τ θ
+ +
⎦
j
⎡
⎣
)
⎤
τ θ
+ +
⎦
(
f kT
2
π
Δ
c
e
是一个复白高斯噪声序列，方差为 2σ 。设
(
1
= +
)
⎤
τ θ
+ +
⎦
(
f kT
c
v
k
x
k
2
π
Δ
+
e
)
⎡
⎣
j
x
k
(3-1)
=
x
k I
,
+
jx
k Q
,
，于
- 2 -
http://www.paper.edu.cn
1
+
x
k
=
(
1
⎡
⎣
+
x
k I
,
2
)
+
x
2
k Q
,
1 2
⎤
⎦
×
exp
⎛
⎜
⎜
⎝
j
tan
1
−
x
k Q
,
x
+
k I
,
1
⎞
⎟
⎟
⎠
(3-2)
(
exp
)
τ θ
+ + +
)
j
x
k Q
,
tan
⎤
⎦
−
1
jx
x
k Q
,
exp
≈
(3-3)
。因此，加性噪声被转化为等效的相位噪声 ,k Qx ，
k Q
,
(
)
x σ
2
k
2
。定义
，则有：
k Qxφ =
k
,
(
j
f kT
c
2
π
Δ
⎡
⎣
)
⎤
τ θ
+ +
⎦
≈
e
2
π
Δ
(
f kT
c
)
τ θ φ
+ + +
k
j
⎡
⎣
⎤
⎦
(3-4)
当
SNR 时，
1
通过以上近似，得到
方差为 (
var
x
k Q
,
=
)
=
e
=
kz
0.5var
x
1
≈
+
k
(
j
f kT
2
⎡
e π
Δ
⎣
c
(
)
⎤
τ θ
+ +
⎦
=
)
z
其中 kφ 是一个零均值白高斯噪声，方差为 2 2σ 。
k
+
v
k
(
1
= +
x
k
)
e
2
π
Δ
(
f kT
c
j
⎡
⎣
通过以上计算，可以得到下式：
(3-5)
k
1
+
z
z
}
z
{
{
arg
Δ =
k
arg
=
cfTπΔ 的带噪声分量的均值，通过{ }kz 序列可以获得(
是 2
{ }
z
arg
−
k
}
fT
2
*
π
= Δ
c
φ φ
k
k
k N
≤ ≤
,1
+
−
−
1
1
+
1
+
k
k
k
k
z
z+
1
}*
显然， {
)1N − 个测
arg
量值。由式(3-5)可知，对于频率偏移的估计问题即为对一个有色高斯噪声过程均值的估计。
该过程实际上是一个系数为 1 和-1 的滑动平均。式(3-5)的线性模型的最小方差无偏（MVU）
估计通过最小化下式得到：
(
Δ
J
2
2
π
− Δ
π
=
− Δ
其中 [
， [
= ，C 是一个(
T
N
1,1,
1
矩阵。于是最小方差无偏估计为：
(3-6)
)
1
− 维的 kΔ 的协方差
)
(
1 C Δ
fT
c
]
,1 T
)
1
fT
c
)
(
1
− ×
= Δ Δ
N
Δ
N −
1
Δ
]
,
,
,
T
−
1
1
2
估计值的方差为：
ˆ
f
Δ =
1
Tπ
2
c
×
1 C Δ
T
1
−
1 C 1
T
1
−
(3-7)
var
(
)
ˆ
f
Δ =
1
Tπ
4
2
2
c
(3-8)
ˆfΔ 是一个无偏的高斯随机变量，与观测值呈线性关系。为了计算 1−C ，首先注意 kΔ 是一个
b
实的滑动平均过程，噪声方差为 2 2σ ，系数为 0
= − 。因此，协方差为：
1 C 1
1
T
−
1
×
1
c
( )
0
=
b
2
0
+
b
2
1
b=
11,
)
=
2
σ
(
2
σ
2
)
1
− =
)
=
0
= −
2
σ
2
2
σ
2
b b
0 1
2
≥
k
c
c
=
( )
1
(
(
c k
由此可知，该协方差矩阵为以下形式：
1
−
2
C
=
2
σ
2
⎛
⎜
⎜
⎜
⎜
⎝
0
0
0
1
−
2
0
0
1
−
0
0
0
1
−
⎞
⎟
⎟
⎟
⎟
2 N
⎠
(
) (
1
− ×
N
)
1
−
- 3 -
(
N
)
1
− ×
(
N
)
− 维矩阵的(
1
,i
于是得到：
−
1
C
⎡
⎣
⎤ =
⎦
ij
)
j 元素的倒数由下式给出：
2 min ,
(
i
2
σ
ij
N
−
≤
1
)
j
i
⎡
⎢
⎣
⎤
⎥
⎦
,
http://www.paper.edu.cn
j N
≤
−
1
(3-9)
1 C Δ
T
1
−
=
其中{ }kγ 是一个窗函数，对称点为
k N=
1 C 1
T
1
−
)
1
2
(
N N
−
=
6
2
σ
(
)
N N
1
−
6
2
σ
。
N
2
2
k
1
−
Δ∑
γ
k
1
=
k
(3-10)
N
最终，得到 fΔ 的估计值为：
γ
k
3
= ⋅
2
N
2
−
1
⎡
1
⎢
⎢
⎣
−
2
k N
−
N
⎛
⎜
⎝
2
⎞
⎟
⎠
⎤
⎥
⎥
⎦
,
k
=
1,2,
,
N
−
1
(3-11)
3.2 Fitz 算法
ˆ
f
Δ =
1
T
2
π
kc
N
1
−
γ
k
∑
1
=
arg
{
z
k
1
+
*
z
k
}
(3-12)
Fitz 算法[3]通过计算 kz 的互相关系数实现，是一个近似的最大似然估计。如式(2-4)所示
的正弦信号频率的最大似然估计由下式给出：
(3-13)
其中 fΔ 是 fΔ 的瞬时值，是通过最大化 fΔ 的最大似然函数得到的。似然函数由周期图得到：
1
=
k
×
arg max
z e
k
=
ˆ
f
Δ
ML
1
T
2
π
c
2
−
j
fT k
2
π
Δ
c
N
∑
L
f
Δ
( )
z
−
j
fT k
2
π
Δ
c
z e
k
2
=
N
∑
k
1
=
由式(3-14)，令互相关系数为 0 得到：
N
N
∑∑
k
1
=
m
1
=
2
z z e π
*
Δ
k m
−
j
fT k m
−
(
c
)
(3-14)
(3-15)
(3-16)
重新整理上式得到：
N
N
∑∑
k
1
=
m
1
=
(
2
k m z z e π−
Δ
*
k m
−
j
)
fT k m
−
(
c
)
=
0
Im
⎧
⎨
⎩
N
1
−
∑
m
1
=
m N m R m e π
fT m
2
Δ
−
−
j
c
(
N
(
)
)
=
0
⎫
⎬
⎭
其中 (
NR m 表示序列 kz 的估计的自相关，定义为：
)
N
1
− ∑
N m
(
)
1
−
≤
≤
i m
1
= +
*
i m
−
m N
R m
N
z z
i
注意到式(3-16)中括号内的部分为估计自相关 (
NR m 的离散傅里叶变换的形式，通过一个
窗函数 (
)
0m = 附近，
相关系数 (
NR m 包含很少的或者根本没有频率偏移信息，这是因为这些值是通过相隔很近
的信号值得到的。另一方面，当 m 接近于 N 时， (
NR m 是一个 kz 自相关的不准确估计，
w m m N m m
进行加权。由加权函数发现，在
−…
N
,1
)
1,2,
),
=
−
=
1
)
)
(
,
(3-17)
- 4 -
因为式(3-17)中求和元素的数量很少。将靠近 m N= 的不可靠自相关值舍弃，并且用一个全
1 的序列替代 (
)w m 之后，得到一个次优的频率偏移估计：
⎫ =
⎬
⎭
R m e π−
fT m
2
Δ
N
∑
Im
⎧
⎨
⎩
(
)
0
1
=
M
m
j
c
由于自相关函数有如下形式：
所以：
当 N 较大时有：
NR m e
=
(
)
j
2
πΔ
fT m
c
+
noise
arg
{
(
E R m
(
N
)
}
)
fT mπ= Δ
2
c
j
−
(
(
Im
fT m
2
Δ
π
)
R m e
N
)
c
≈
≈
sin arg
(
{
arg
{
(
R m
N
}
)
(
R m
N
}
)
2
− Δ
π
2
π
− Δ
fT m
c
fT m
c
于是，式(3-18)当 N 较大时近似为：
{
arg
M
∑
⎡
⎣
m
1
=
对式(3-22)进行代数计算，得到 fΔ 的估计值为：
R m
N
(
}
)
− Δ
fT mπ
2
c
≈
0
⎤
⎦
http://www.paper.edu.cn
(3-18)
(3-19)
(3-20)
(3-21)
(3-22)
)
M
∑
m
1
=
ˆ
f
Δ
ML
≈
3.3 L&R 算法
arg
{
R m
N
(
}
)
T
2
π
c
M
∑
m
1
=
m
=
1
M M
(
π
+
)
1
M
∑
1
=
T
mc
arg
{
R m
N
(
}
)
(3-23)
信道模型如式(2-4)所示，通过寻找式(3-14)给出的似然函数的最大值获得频率偏移的估
计即为该算法。L&R 算法[4]的分析与 Fitz 算法的分析基本相同，不同之处在于对式(3-18)采
用不同的替代形式。
用泰勒级数展开的形式对式(3-18)进行替代，进行计算得到：
R m
N
基于上述假设 (
)
=
mv ，于是：
1
量，
ˆ
f
Δ ≈
1
T
2
π
s
exp
(
j
fmT
2
π
Δ
c
)
M
1
=
m
m
M
∑
∑
m
1
=
v
+
m
(
Im
{
{
1
≈ +
Re
R m
N
}
)
}
)
j m fT
2
Δ
π
c
R m
N
(
(3-24)
+
，其中 mv 是一个噪声分
v
m
M
∑
m
1
=
Im
{
R m
N
(
}
)
≈
M
arg
M
∑
m
1
=
m
Re
{
R m
N
(
}
)
≈
R m
N
(
)
⎫
⎬
⎭
+
)
1
k
M
⎧
∑
⎨
⎩
1
=
(
M M
2
(3-25)
(3-26)
将(3-25)和(3-26)带入式(3-24)中，最终得到 fΔ 的估计为：
- 5 -
3.4 Kay&R 算法
ˆ
f
Δ =
1
+
)
1
T
c
arg
⎧
⎨
⎩
(
π
M
M
∑
m
1
=
http://www.paper.edu.cn
(3-27)
R m
N
(
)
⎫
⎬
⎭
Kay&R 算法[5]通过计算 (
)
z k 的自相关和该自相关值序列的相位增量来实现。将式(3-19)
转化为如下形式：
j
其中 '
φ
m
e
+
1
v
'
m
e
π−
j m fT
2
c
Δ
Δ
e
=
j m fT
2
π
c
R
+
m
。考虑下式：
v
'
m
=
(
j
2
e π
m fT
c
Δ
'
φ
+
m
)
f
Δ <
(
T
1 2 c
)
若
*
{
arg
R R
m
}
m
1
−
， fΔ 的估计表示为：
1
Tπ
2
c
ˆ
f
Δ =
=
fTπ
2
Δ
c
+
'
φ φ
−
'
m
m
1
−
×
arg
{
*
R R
m
m
1
−
}
在平滑噪声的影响之后，可以得到 fΔ 的最终估计为：
{
)
M N M
1
− + −
MN
N
3
+
−
1
×∑
Tπ
2
mc
)(
N m N m
−
M M
6
4
ˆ
f
Δ =
R R
m
arg
w
m
w
m
−
=
3
⎡
⎣
(
(
1
=
1
−
M
m
2
2
*
}
−
)
1
(
(3-28)
(3-29)
(3-30)
(3-31)
(3-32)
)
⎤
⎦
4. Crame-Rao 下界
接收信号为一个样本矢量：
荡器 {
exp
2j
}
ftπΔ 的频率偏移 fΔ 的最大似然估计问题：
=R
[
r r
,
1
2
,...,
r −
N
1
T
]
。由采样信号的观测值开始考虑复数振
(
)
θ
+
j
fkT
2
π
Δ
s
e
=
r
k
k N
(4-1)
， ,k cn 和 ,k sn 是独立高斯噪声采样，
其中 sT 是采样间隔；θ是一个未知相位；
n
k
均值为 0，方差为 2 2σ 。此信号模型与式(2-4)一致，所以，可以使用该 Crame-Rao 下界
（CRLB，Cramer-Rao Lower Bound）[6]作为频偏估计算法性能评判准则。
, 1
≤ ≤
jn
+
n
+
k
n
=
k c
,
k s
,
因此，
其中
(
cos 2
=
fkT
π
Δ
s
r
k i
,
于是，当未知参数矢量α 时，采样矢量 R 的联合概率密度函数（PDF，probability density
+ 。
n
k s
,
+
)
θ
r
k
r
=
k i
,
r
+ ，
k q
,
n
k c
,
k N
jr
, , 1
≤ ≤
+
k q
)
(
fkT
sin 2
θ
=
π
Δ
+
s
(4-2)
function）由下式给出：
f
(
R α
;
)
=
N
exp
1
2
πσ
⎛
⎜
⎝
⎞
⎟
⎠
−
⎧
⎨
⎩
1
2
σ
N
1
−
∑
k
=
0
r
k i
,
−
μ
k
2
)
+
(
r
k q
,
ν
−
k
(
⎡
⎢
⎣
2
)
⎤
⎥
⎦
⎫
⎬
⎭
其中，如果 fΔ 和θ均未知，则：
α
[
= Δ
T
]
f θ
,
- 6 -
(4-3)
(4-4)
http://www.paper.edu.cn
=
=
μ
k
ν
k
)
θ
+
)
+
θ
(
cos 2
(
sin 2
fkT
π
Δ
s
fkT
π
Δ
s
(4-5)
(4-6)
在一个估计（或者测量）系统中，有一些参数能够指示利用可用数据（观测值）可以进
行的最优估计是很重要的。均方根（RMS，root mean square）误差就是这样一个重要的参数，
经常被用来作为一个系统准确度的测量标准。Crame-Rao 下界是任何一个以式(2-4)和(4-1)为
信号模型的频率偏移变量估计的理论的下限（也就是，任何估计都不能超过它）。因此，本
文引用 CRLB 作为频偏估计算法性能的评判标准。
无偏估计的 CRLB 是由费舍尔信息矩阵（Fisher information matrix） J 对角线元素的倒
数给出，费舍尔信息矩阵 J 的典型元素由下式给出：
{
E H
{
E H H
α α
j
其中，期望值与采样矢量 R 有关，为：
(4-7)
= −
ijJ
}
}
αα
j
=
i
i
则下界为：
H
∂
α α
∂
i
=
i
log
f
(
)
R α
;
其中， ˆiα是 iα的估计值， iiJ 表示 1−J 的第i 个对角线元素。
i
var
{ }ˆ
Jα ≥
ii
(4-8)
(4-9)
当 (
)
f R α 是由式(4-3)给出时，费舍尔信息矩阵 J 的元素为：
;
J
ij
=
1
−
2 N
∑
2
σ
=
0
k
⎡
⎢
⎢
⎣
k
v
μ μ
∂
∂
k
k
α α α α
∂
∂
j
v
∂
k
∂
∂
∂
+
i
j
i
⎤
⎥
⎥
⎦
(4-10)
式(4-10)中的下标i 和 j 只表示α 中的未知元素。最一般的情况即是α 中的所有元素均未知，
则由式(4-10)得到矩阵 J 为：
其中
于是得到 1−J 如下式所示：
J
=
2
T Q
4
2
2
π
s
T P
2
2
σ π
s
⎡
⎢
⎣
T P
2
π
s
N
⎤
⎥
⎦
P
=
Q
=
N
1
−
2
=∑
k
k
=
0
)
1
N
1
−
=∑
k
(
N N
=
0
k
−
(
N N
2
)(
1 2
6
−
N
−
)
1
3
2
σ
(
T N N
2
2
2
π
s
当相位未知时，频率偏移估计的 CRLB 为：
1
J
=
=
J
J
−
2
1
*
2
⎛
×⎜
⎝
N
T P
2
π
s
−
)
1
−
T P
2
π
−
s
T Q
4
2
2
π
s
⎞
⎟
⎠
var
(
)
ˆ
f
Δ ≥
3
2
σ
(
T N N
2
2
2
π
s
2
)
1
−
- 7 -
(4-11)
(4-12)
(4-13)
(4-14)
(4-15)
http://www.paper.edu.cn
5. 算法改进
考虑到频偏估计的下界近似与观测序列长度的立方成反比，即观测序列的长度越长，观
测结果越精确。
因此，首先使用训练序列（Midamble 码）进行频偏估计，获得一个粗略的频偏估计值，
将这个频偏估计值补偿之后，再使用用户数据和 Midamble 码序列一起进行频偏估计，获得
一个精确的估计值，该值作为粗略的频偏估计值的补充。即：
ˆ
ˆ
f
f
Δ = Δ
mid
+ Δ
ˆ
f
ud
mid
fΔ 为由使用 Midamble 码序列进行估计获得的频偏估计值， ˆ
(5-1)
其中， ˆ
udfΔ 为由使用用户数
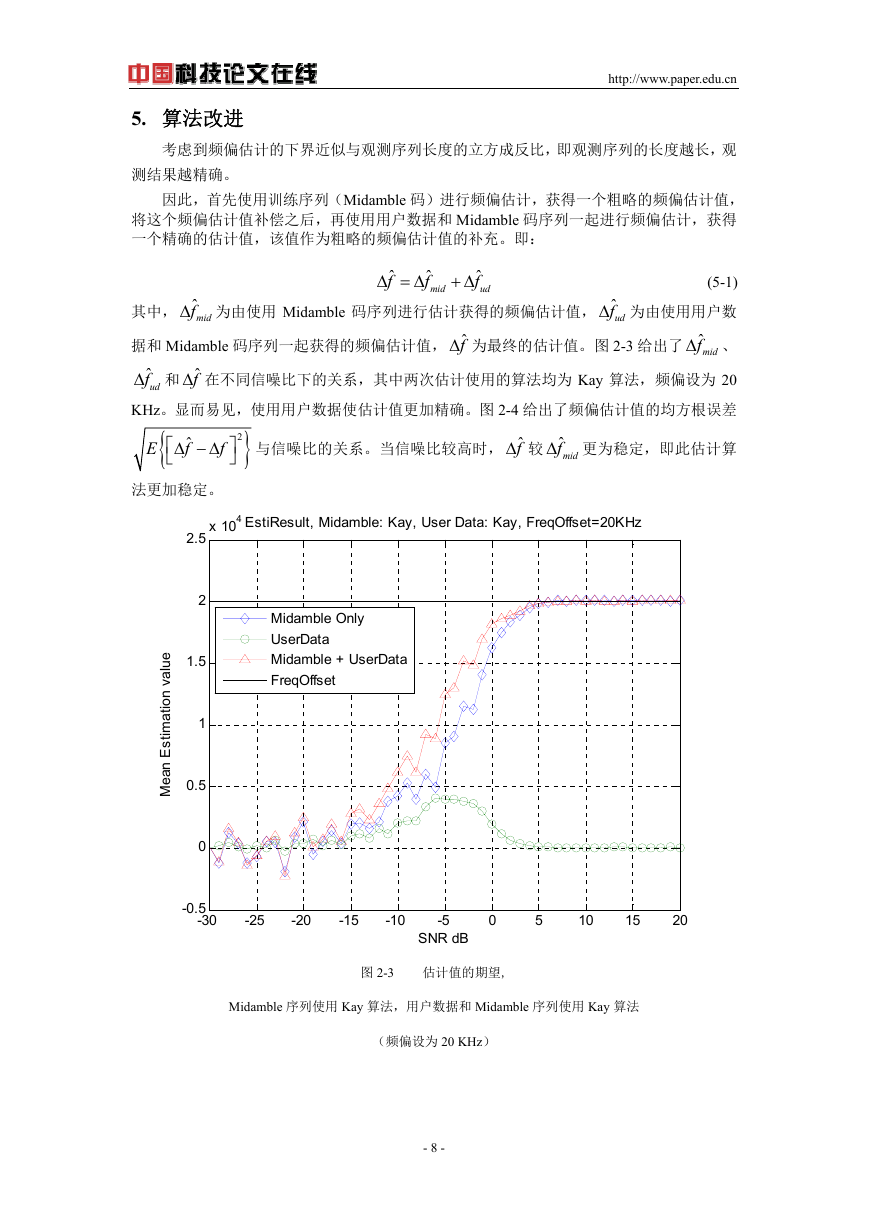
据和 Midamble 码序列一起获得的频偏估计值， ˆfΔ 为最终的估计值。图 2-3 给出了 ˆ
fΔ 、
ˆ
udfΔ 和 ˆfΔ 在不同信噪比下的关系，其中两次估计使用的算法均为 Kay 算法，频偏设为 20
KHz。显而易见，使用用户数据使估计值更加精确。图 2-4 给出了频偏估计值的均方根误差
{
}2
⎦ 与信噪比的关系。当信噪比较高时， ˆfΔ 较 ˆ
⎤
fΔ 更为稳定，即此估计算
E
ˆ
f
Δ − Δ
f
mid
mid
⎡
⎣
法更加稳定。
x 104 EstiResult, Midamble: Kay, User Data: Kay, FreqOffset=20KHz
Midamble Only
UserData
Midamble + UserData
FreqOffset
2.5
2
1.5
1
0.5
0
l
e
u
a
v
n
o
i
t
a
m
i
t
s
E
n
a
e
M
-0.5
-30
-25
-20
-15
-10
-5
SNR dB
0
5
10
15
20
图 2-3 估计值的期望,
Midamble 序列使用 Kay 算法，用户数据和 Midamble 序列使用 Kay 算法
（频偏设为 20 KHz）
- 8 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
