脊波和曲波变换.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：4.45M 资料格式：pdf 举报版权申诉

zifa987654321-4188795-4744300845200028723.pdf-第1页.png

第1页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第2页.png

第2页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第3页.png

第3页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第4页.png

第4页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第5页.png

第5页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第6页.png

第6页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第7页.png

第7页 / 共96页

zifa987654321-4188795-4744300845200028723.pdf-第8页.png

第8页 / 共96页

文本预览

第三章脊波和曲波变换自然图像中包含有大量的纹理特征, 线奇异性表现比较突出, 小波变换不能达到最优的逼近。为了克服小波的这种不足, Candes等人提出了一种新的多尺度变换——Ridgelet变换 (Ridgelet Transform) Joint Laboratory of Shantou and Xiamen University, 2008 1

3.1 Ridgelet 变换的定义 3.1.1 一维Ridgelet变换引入函数集： Γ = { γ = ( a u b a b R a , , ∈ , , ) ; (3-1) > 0, u ∈ S d − }1 是d 维空间的单位球面。记多维空间的Fourier 变换为： ˆ f ( ) ξ = ix − ⋅ ξ e ∫ ( ) f x dx x R ∈ , d (3-2) Joint Laboratory of Shantou and Xiamen University, 2008 2

定义3.1：取一光滑的一元函数： CRT a b , ) , θ ( ψ= ∫ ( R 2 ) ( a b , , θ f X f X dX ) ( ) 其中 ψ → : R R 并满足容许条件 ∫ t dtψ = ( ) 0 Joint Laboratory of Shantou and Xiamen University, 2008 3

定义一个多元函数： γψ ( ) x = a ⎛ 1/ 2 ψ− ⎜ ⎝ ⋅ u x b ⋅ − a ⎞ ⎟ ⎠ (3-3) γψ 则称为由容许条件生成的Ridgelet[2]。其中称为 Ridgelet 的尺度参数，表示方向，为位置参数。是一个不可分离变量的基本函数生成元，能够生成一组面向目标的 Ridgelet 族。 ψ u b a γψ Joint Laboratory of Shantou and Xiamen University, 2008 4

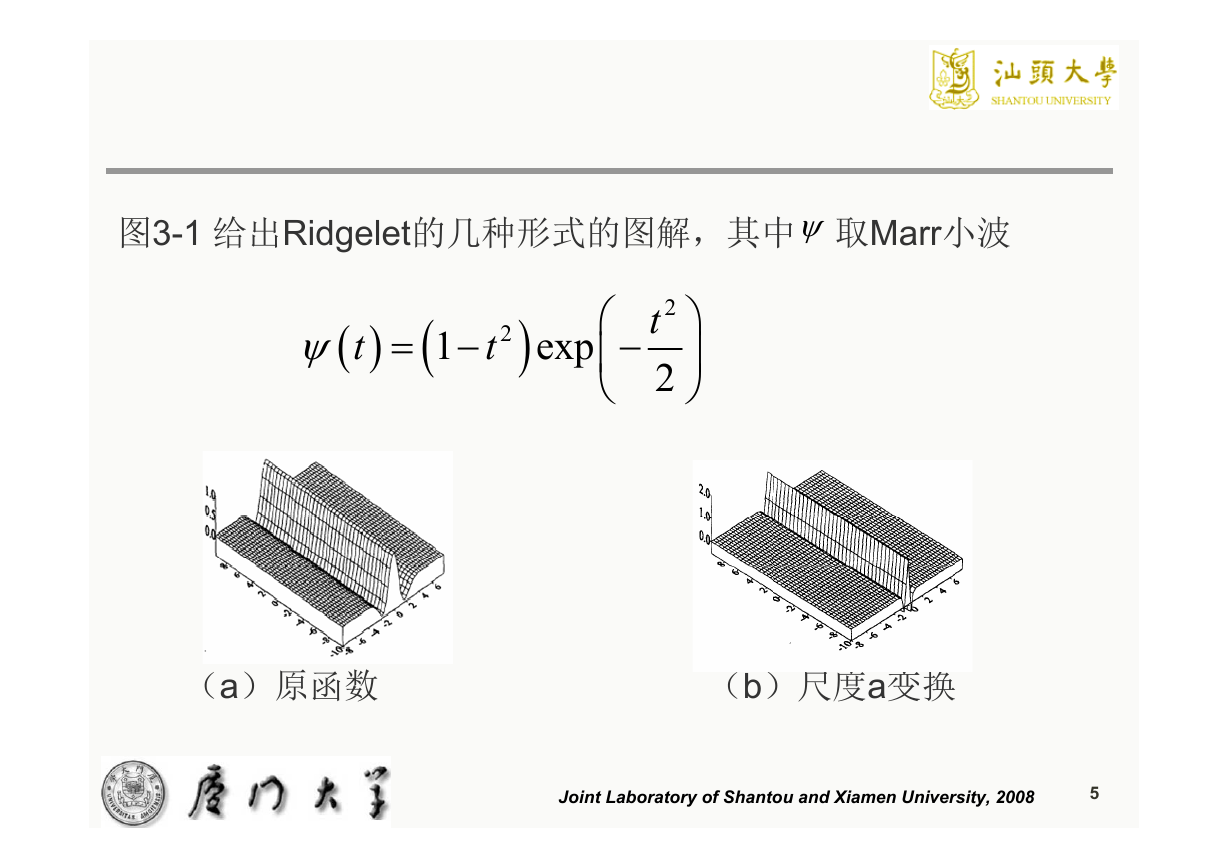
图3-1 给出Ridgelet的几种形式的图解，其中取Marr小波 ψ ψ ( ) t ( 1 = − 2 t ) exp ⎛ −⎜ ⎝ t 2 2 ⎞ ⎟ ⎠ （a）原函数（b）尺度a变换 Joint Laboratory of Shantou and Xiamen University, 2008 5

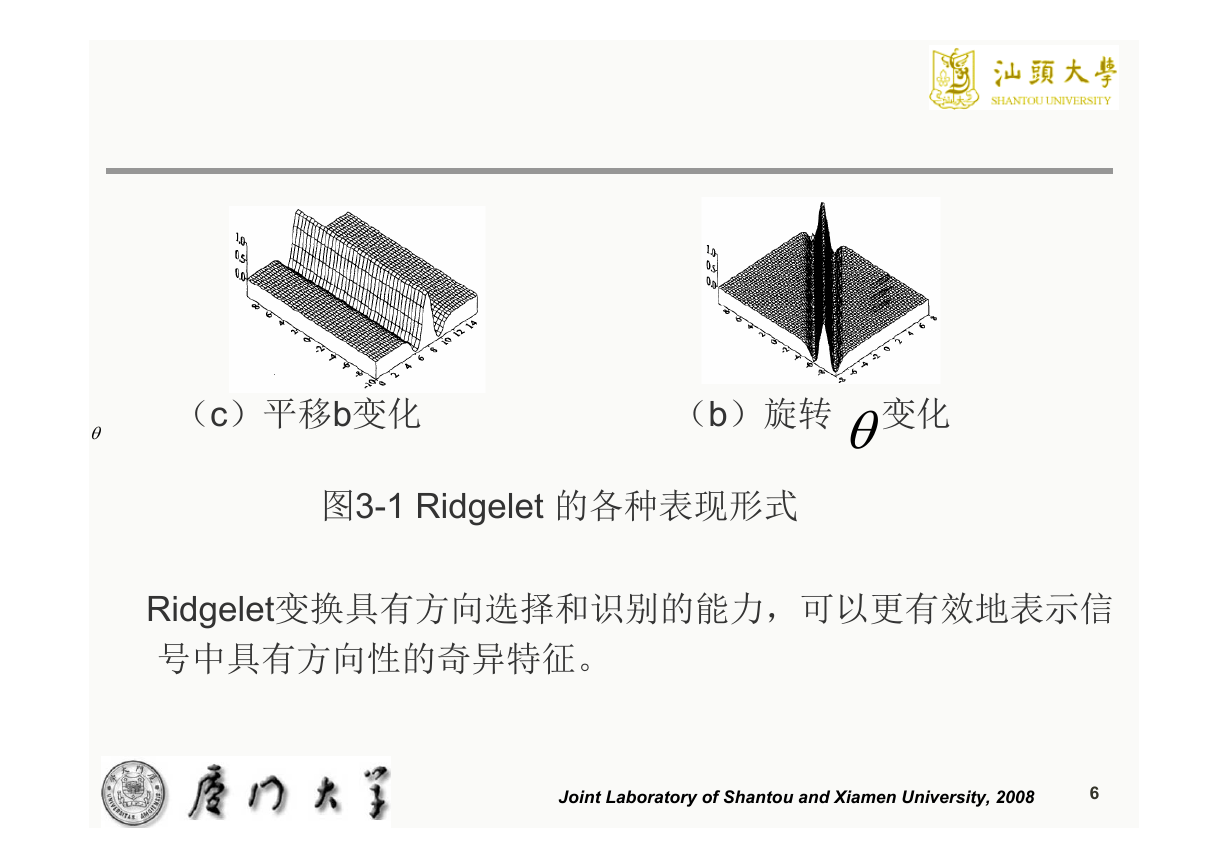
（c）平移b变化 θ （b）旋转变化 θ 图3-1 Ridgelet 的各种表现形式 Ridgelet变换具有方向选择和识别的能力，可以更有效地表示信号中具有方向性的奇异特征。 Joint Laboratory of Shantou and Xiamen University, 2008 6

3.1.2 二维Ridgelet变换二维连续Ridgelet变换（Continuous Ridgelet Transform， CRT）在域的定义为[2]： ψ= ∫ ( X f X dX CRT a b , ) , θ ) ( a b , , θ ( ) ( ) f 2 R (3-4) 反变换公式： ( f X ) 2 π ∞ ∞ = ∫ ∫ ∫ 0 −∞ 0 CRT a b , f ( ) , θψ a b , , θ ( X ) da a 3 db d θ 4 π (3-5) Joint Laboratory of Shantou and Xiamen University, 2008 7

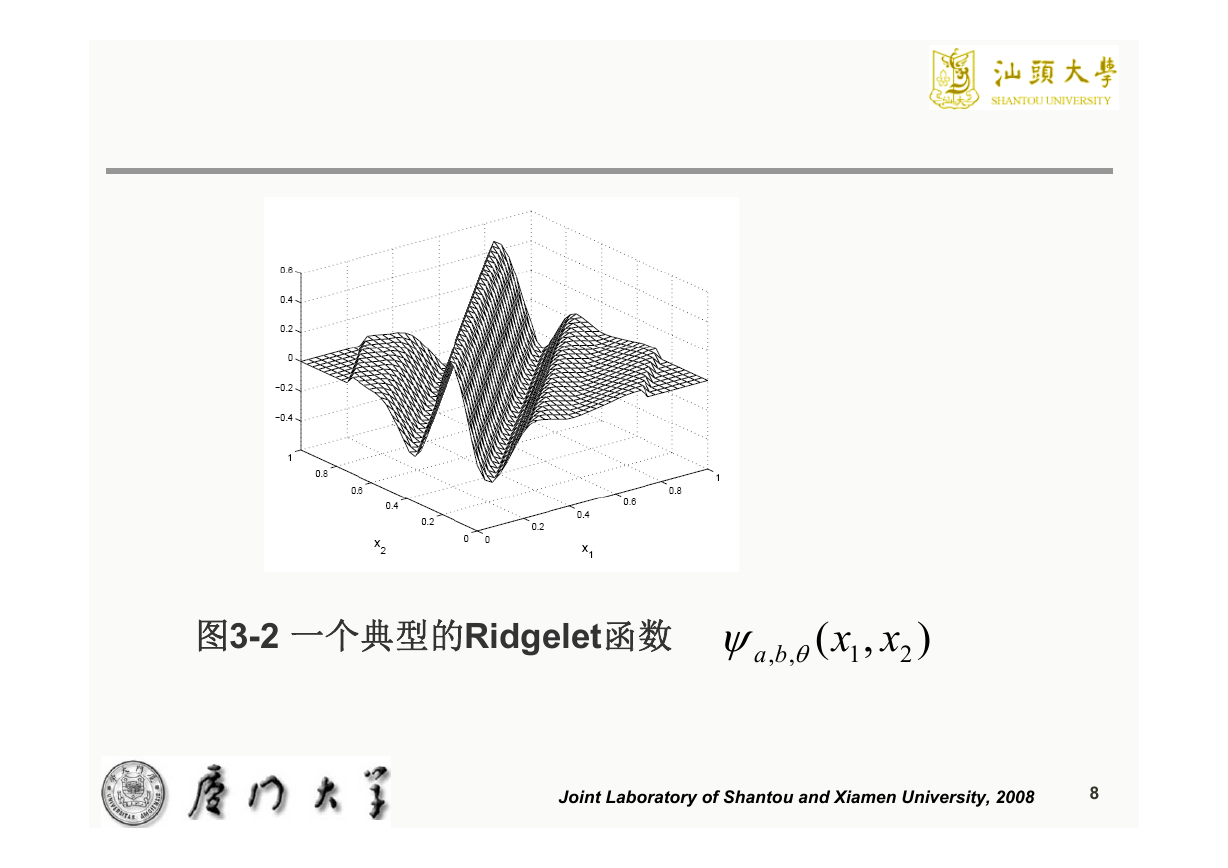
图3-2 一个典型的Ridgelet函数 ( θψ a b , , x x , 1 2 ) Joint Laboratory of Shantou and Xiamen University, 2008 8

分享到：

赞收藏

资料库

脊波和曲波变换.pdf

相关推荐

课程资源

热门标签

最新资料