第1页 / 共30页
第2页 / 共30页
第3页 / 共30页
第4页 / 共30页
第5页 / 共30页
第6页 / 共30页
第7页 / 共30页
第8页 / 共30页
matlab多元非线性回归教程.doc
matlab回归（拟合）总结
前言
一、回归命令
二、多元回归分析
例1
例2
例3
三、非线性回归（拟合）
例1
例2
例3
例4
四、非线性回归或曲线回归问题
作业
关于利用Matab进行指定非线性拟合的问题（转载）
matlab 回归（拟合）总结
前言
1、学三条命令
polyfit(x,y,n)---拟合成一元幂函数（一元多次）
regress(y,x)----可以多元，
nlinfit(x,y,’fun’,beta0)
(可用于任何类型的函数，任意多元函数，应用范围最主，最万
能的)
2、同一个问题，这三条命令都可以使用，但结果肯定是不同的，因为拟合的近似结果，
没有唯一的标准的答案。相当于咨询多个专家。
3、回归的操作步骤：
根据图形（实际点），选配一条恰当的函数形式（类型）---需要数学理论与基础和经验。
（并写出该函数表达式的一般形式，含待定系数）------选用某条回归命令求出所有的待定系
数。所以可以说，回归就是求待定系数的过程（需确定函数的形式）
一、回归命令
一元多次拟合 polyfit(x,y,n);一元回归 polyfit;多元回归 regress---nlinfit(非线性)
二、多元回归分析
对于多元线性回归模型(其实可以是非线性，它通用性极高)：
y
0
x
1
1
x
p
p
e
设变量 1
,
x x
2
,
,p
y
x
x
的 n 组观测值为 1
i
(
,
x
i
2
,
x
ip
,
y
i
)
i
1,2,
,
n
记
x
x
1
x
x
11
x
21
x
12
x
22
1
1
2
p
1
x
与线性代数中的线性方程组相同（），拟合成多元函数---regress
y
1
y
ny
，
y
，则
np
x
1
n
x
n
2
p
2
0
1
p
的估计值为排列方式
使用格式：左边用 b=[b, bint, r, rint, stats]右边用=regress(y, x)或 regress(y, x, alpha)
---命令中是先 y 后 x,
---须构造好矩阵 x(x 中的每列与目标函数的一项对应)
---并且 x 要在最前面额外添加全 1 列/对应于常数项
---y 必须是列向量
---结果是从常数项开始---与 polyfit 的不同。）
其中： b 为回归系数，的估计值(第一个为常数项)，bint 为回归系数的区间估计，r: 残
差 ，rint: 残差的置信区间，stats: 用于检验回归模型的统计量，有四个数值：相关系数 r2、
F 值、与 F 对应的概率 p 和残差的方差（前两个越大越好，后两个越小越好），alpha: 显著
性水平（缺省时为 0.05，即置信水平为 95%），（alpha 不影响 b,只影响 bint(区间估计)。它越
小，即置信度越高，则 bint 范围越大。显著水平越高，则区间就越小）（返回五个结果）---
如有 n 个自变量-有误（n 个待定系数），则 b 中就有 n+1 个系数（含常数项，---第一项为常
数项）(b---b 的范围/置信区间---残差 r---r 的置信区间 rint-----点估计----区间估计
此段上课时不要：---- 如果 i 的置信区间（bint 的第 1i 行）不包含 0，则在显著水
平为时拒绝
i 的假设，认为变量 ix 是显著的．*******(而 rint 残差的区间应包含 0
0
则更好)。b,y 等均为列向量,x 为矩阵(表示了一组实际的数据)必须在 x 第一列添加一个全 1
列。----对应于常数项-------而 nlinfit 不能额外添加全 1 列。结果的系数就是与此矩阵相对应
的（常数项，x1,x2,……xn）。（结果与参数个数：1/5=2/3-----y,x 顺序---x 要额外添加全 1 列）
而 nlinfit:1/3=4------x,y 顺序---x 不能额外添加全 1 列，---需编程序，用于模仿需拟合的
函数的任意形式，一定两个参数，一为系数数组，二为自变量矩阵（每列为一个自变量）
有 n 个变量---不准确，x 中就有 n 列,再添加一个全 1 列（相当于常数项），就变为 n+1
列，则结果中就有 n+1 个系数。
x 需要经过加工，如添加全 1 列，可能还要添加其他需要的变换数据。
相关系数 r2 越接近 1，说明回归方程越显著；(r2 越大越接近 1 越好)F 越大，说明回归
方程越显著；（F 越大越好）与 F 对应的概率 p 越小越好，一定要 P
的型式）
重点：
regress(y,x) 重点与难点是如何加工处理矩阵 x。
y 是函数值，一定是只有一列。
也即目标函数的形式是由矩阵 X 来确定
如 s=a+b*x1+c*x2+d*x3+e*x1^2+f*x2*x3+g*x1^2,
一定有一个常数项，且必须放在最前面（即 x 的第一列为全 1 列）
X 中的每一列对应于目标函数中的一项（目标函数有多少项则 x 中就有多少列）
X=[ones, x1, x2, x3, x1.^2, x2.*x3，x1.ˆ2]
(剔除待定系数的形式)
regress:
y/x 顺序，矩阵 X 需要加工处理
nlinfit:
x/y 顺序，X/Y 就是原始的数据，不要做任何的加工。
(即 regress 靠矩阵 X 来确定目标函数的类型形式（所以 X 很复杂，要作很多处理） 而
nlinfit 是靠程序来确定目标函数的类型形式（所以 X 就是原始数据，不要做任何处理）
例 1
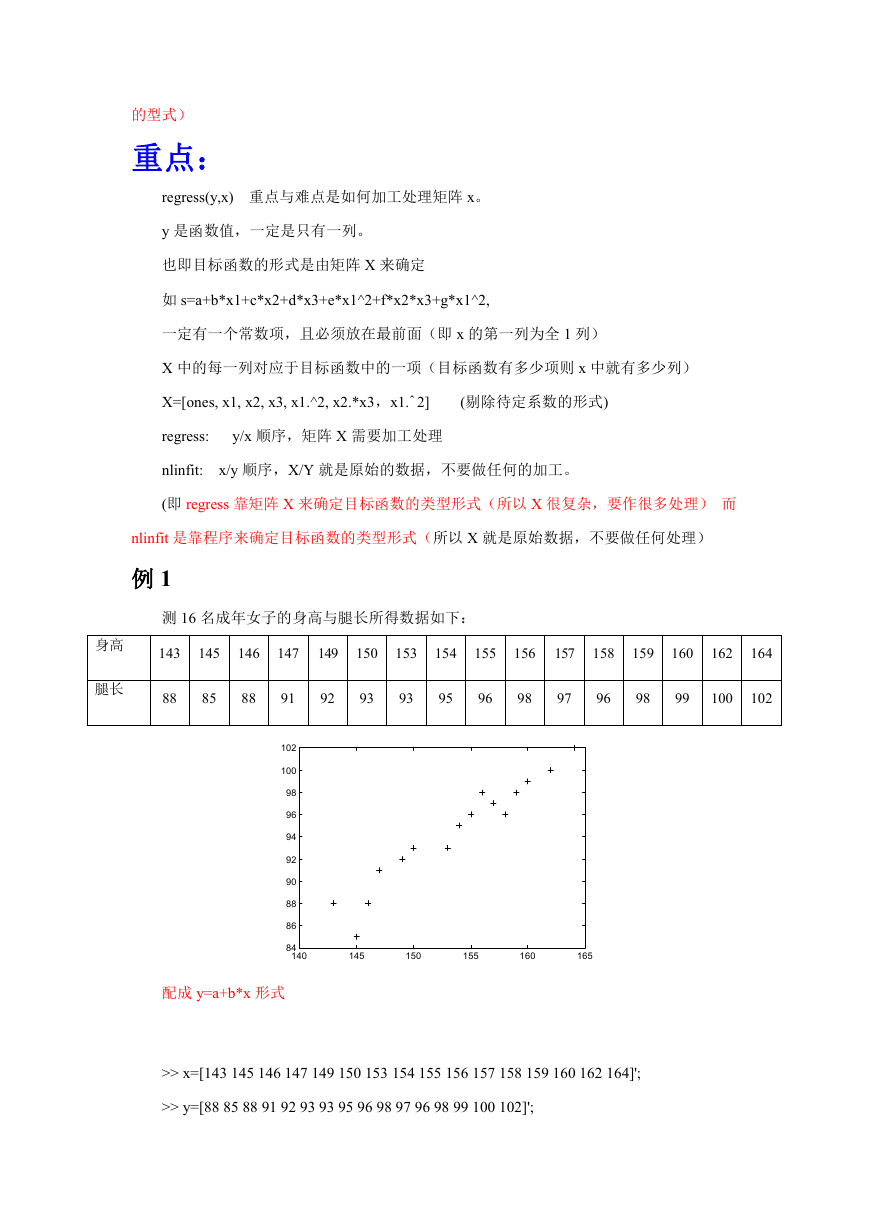
测 16 名成年女子的身高与腿长所得数据如下：
143
145
146
147
149
150
153
154
155
156
157
158
159
160
162
164
88
85
88
91
92
93
93
95
96
98
97
96
98
99
100
102
身高
腿长
102
100
98
96
94
92
90
88
86
84
140
配成 y=a+b*x 形式
145
150
155
160
165
>> x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
>> y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
>> plot(x,y,'r+')
>> z=x;
>> x=[ones(16,1),x];----常数项
>> [b,bint,r,rint,stats]=regress(y,x);---处结果与 polyfit(x,y,1)相同
>>b,bint,stats
得结果：b =
-16.0730
0.7194
bint =
-33.7071
1.5612------每一行为一个区间
0.6047
0.8340
stats = 0.9282 180.9531
0.0000
即
ˆ
0
.16
ˆ,073
1
.0
7194
； 0ˆ 的 置 信 区 间 为 [-33.7017 ， 1.5612],
1ˆ 的 置 信 区 间 为
[0.6047,0.834]; r2=0.9282, F=180.9531, p=0.0。p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
>> [b,bint,r,rint,stats]=regress(Y,X,0.05);-----结果相同
>> [b,bint,r,rint,stats]=regress(Y,X,0.03);
>> polyfit(x,y,1)-----当为一元时（也只有一组数），则结果与 regress 是相同的，只是
命令中 x,y 要交换顺序，结果的系数排列顺序完全相反，x 中不需要全 1 列。
ans =0.7194
-16.0730--此题也可用 polyfit 求解，杀鸡用牛刀，脖子被切断。
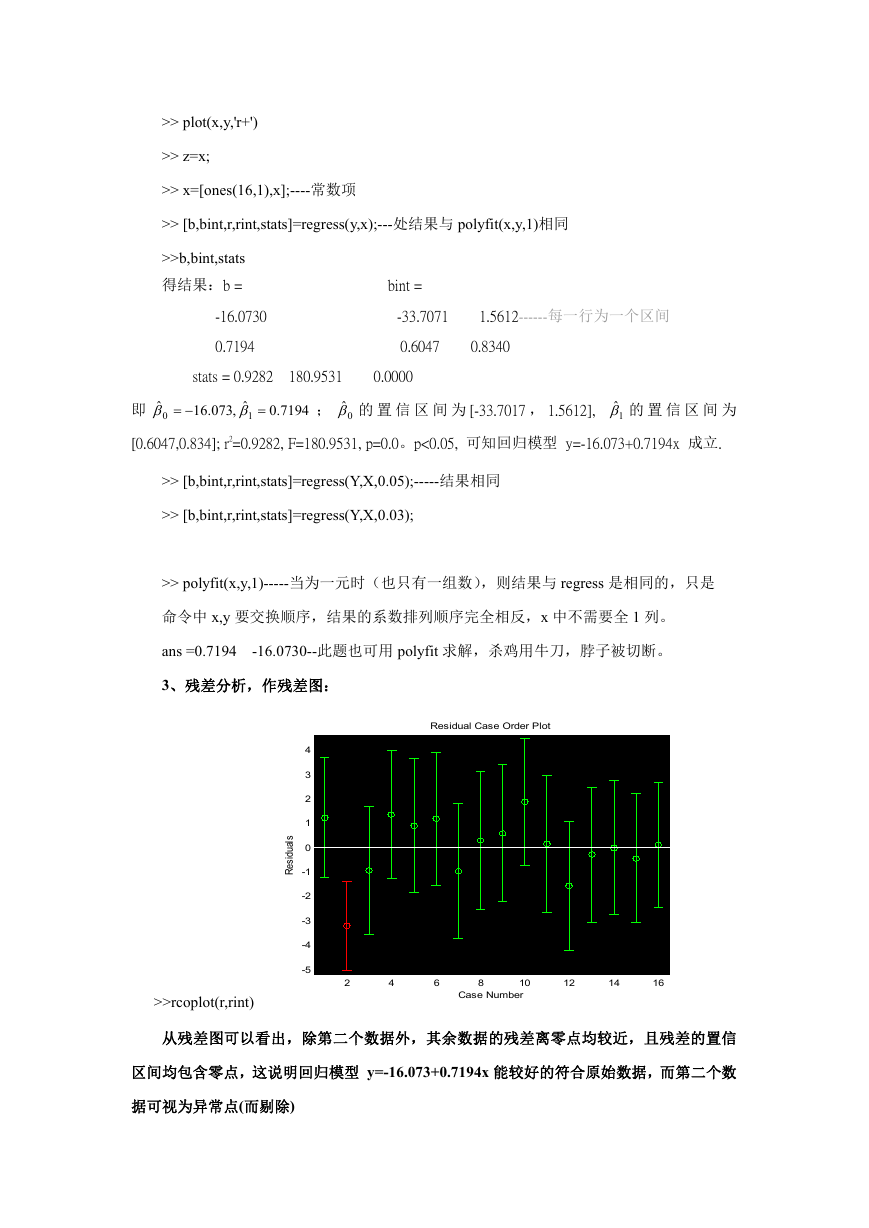
3、残差分析，作残差图：
Residual Case Order Plot
l
s
a
u
d
s
e
R
i
4
3
2
1
0
-1
-2
-3
-4
-5
>>rcoplot(r,rint)
2
4
6
8
Case Number
10
12
14
16
从残差图可以看出，除第二个数据外，其余数据的残差离零点均较近，且残差的置信
区间均包含零点，这说明回归模型 y=-16.073+0.7194x 能较好的符合原始数据，而第二个数
据可视为异常点(而剔除)
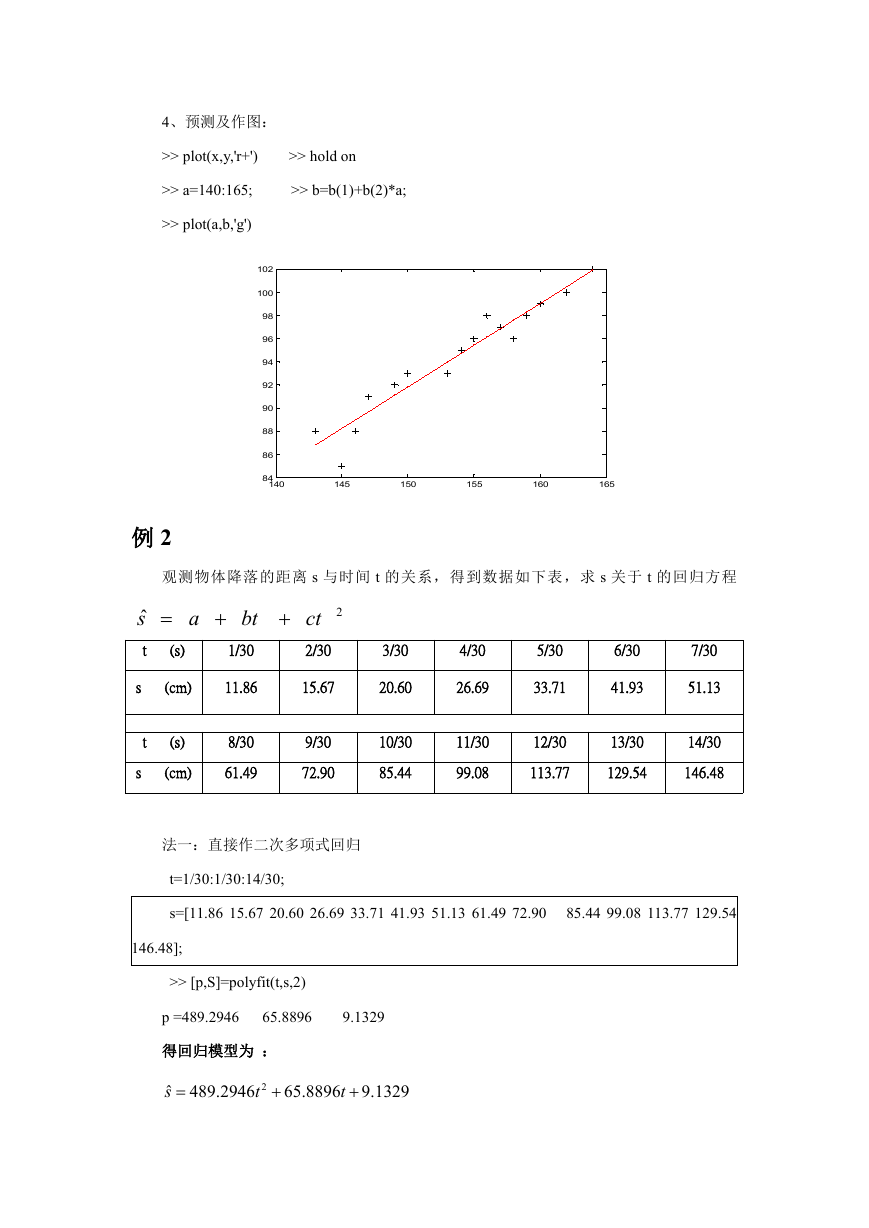
4、预测及作图：
>> plot(x,y,'r+')
>> hold on
>> a=140:165;
>> b=b(1)+b(2)*a;
>> plot(a,b,'g')
102
100
98
96
94
92
90
88
86
84
140
145
150
155
160
165
例 2
观测物体降落的距离 s 与时间 t 的关系，得到数据如下表，求 s 关于 t 的回归方程
ˆ
s
t
a
(s)
bt
1/30
2
ct
2/30
3/30
4/30
5/30
6/30
7/30
s
(cm)
11.86
15.67
20.60
26.69
33.71
41.93
51.13
t
s
(s)
8/30
(cm)
61.49
9/30
72.90
10/30
85.44
11/30
99.08
12/30
13/30
14/30
113.77
129.54
146.48
法一：直接作二次多项式回归
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90
85.44 99.08 113.77 129.54
146.48];
>> [p,S]=polyfit(t,s,2)
p =489.2946
65.8896
9.1329
得回归模型为 ：
ˆ
s
489
.
2946
t
2
.65
8896
t
.9
1329
方法二----化为多元线性回归：
ˆ
s
a
t=1/30:1/30:14/30;
bt
ct
2
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54
146.48];
>> T=[ones(14,1), t', (t.^2)'] %？？？是否可行？？？等验证...----因为有三个待定系
数，所以有三列，始于常数项
>> [b,bint,r,rint,stats]=regress(s',T);
>> b,stats
b = 9.1329
65.8896
489.2946
stats =1.0e+007 *
0.0000
1.0378
0
0.0000
得回归模型为 ：
.9ˆ
s
1329
.65
8896
t
489
.
2946
t
2
%结果与方法 1 相同
>> T=[ones(14,1),t, (t.^2)'] %？？？是否可行？？？等验证...
polyfit------一元多次
regress----多元一次---其实通过技巧也可以多元多次
regress 最通用的，万能的，表面上是多元一次，其实可以变为多元多次且任意函数，
如 x 有 n 列（不含全 1 列），则表达式中就有 n+1 列（第一个为常数项，其他每项与 x 的列
序相对应）??????此处的说法需进一步验证证……………………………
例 3
设某商品的需求量与消费者的平均收入、商品价格的统计数据如下，建立回归模型，
预测平均收入为 1000、价格为 6 时的商品需求量.
需求量 100
75
80
70
50
65
90
100
110
60
收入
1000
600
1200
500
300
400
1300
1100
1300
300
价格
5
7
6
6
8
7
5
4
3
9
选择纯二次模型，即
y
0
1
x
1
2
x
2
11
x
2
1
22
x
2
2
----用户可以任意设计函数
>> x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
>> x2=[5 7 6
6 8 7 5 4 3 9];
>> y=[100 75 80 70 50 65 90 100 110 60]';
X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)']; %注意技巧性??????
[b,bint,r,rint,stats]=regress(y,X); %这是万能方法??????需进一步验证
>> b,stats
b =
110.5313
0.1464
-26.5709
-0.0001
1.8475
stats = 0.9702
40.6656
0.0005
20.5771
故回归模型为：
y
110
.
5313
.0
1464
x
1
.26
5709
x
2
.0
0001
2
x
1
.1
8475
x
2
2
剩余标准差为 4.5362, 说明此回归模型的显著性较好.
--------(此题还可以用 rstool(X,Y)命令求解，详见回归问题详解)
>> X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)',sin(x1.*x2)',(x1.*exp(x2))'];
>> [b,bint,r,rint,stats]=regress(y,X);
>> b,stats
(个人 2011 年认为，regress 只能用于函数中的每一项只能有一个待定系数的情况，不
能用于 aebx 等的情况)
regress(y,x)
----re 是 y/x 逆置的
---y 是列向量
---须确定目标函数的形式
---x 须构造（通过构造来反映目标函数）
---x 中的每一列与目标函数的一项对应（剔除待定系数）
----首项为常数项（x 的第一列为全 1）
----有函数有 n 项(待定系数),则 x 就有 n 列
----regress 只能解决每项只有一个待定系数的情况且必须有常数项的情况（且每项只有
一个待定系数，即项数与待定系数数目相同）
***其重（难、关键）点：列向量、构造矩阵(X):目标函数中的每项与 X 中的一列对应。
（由 X 来确定目标函数的类型/形式）
三、非线性回归（拟合）
使用格式：beta = nlinfit(x,y, ‘ 程序名’,beta0) [beta,r,J] = nlinfit(X,y,fun,beta0)
X 给定的自变量数据,Y 给定的因变量数据,fun 要拟合的函数模型(句柄函数或者内联函数形
式),beta0 函数模型中待定系数估计初值（即程序的初始实参）beta 返回拟合后的待定系数其
中 beta 为估计出的回归系数；r 为残差；J 为 Jacobian 矩阵
输入数据 x、y 分别为 n*m 矩阵和 n 维列向量，对一元非线性回归，x 为 n 维列向量。
’model’为是事先用 m-文件定义的非线性函数；beta0 为回归系数的初值
可以拟合成任意函数。最通用的，万能的命令
x,y 顺序，x 不需要任何加工，直接用原始数据。（也不需要全 1 列）---所编的程序一定
是两个形参（待定系数/向量，自变量/矩阵：每一列为一个自变量）
结果要看残差的大小和是否有警告信息，如有警告则换一个 b0 初始向量再重新计算。
本程序中也可能要用.* ./ .^如结果中有警告信息，则必须多次换初值来试算难点是编程
序与初值
nlinfit 多 元 任 意 函 数 ， （ 自 己 任 意 设 计 函 数 ， 再 求 待 定 系 数 ） 顺 序
（[b,r,j]=nlinfit(x,y,’…’, b0）y 为列向量；x 为矩阵，无需加全 1 列，x,y 就是原始的数据点，
（x/y 正顺序，所以 x 不要加全 1 列）需预先编程（两个参数，系数向量，各变量的矩阵/每
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
