logo资料库

公交车线路选择的优化模型.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.64M 资料格式：doc 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    公交车线路选择的优化模型 摘要：本题是一个公交线路选择的优化问题，考虑到公交乘客路线选择的影响因 素有换乘次数、出行耗时和出行费用等多个方面，要得到最佳的公交车线路，就 必须综合考虑这些方面，进行多目标规划。 通过对公交乘客出行心理的了解与研究得知：一般乘客对上述的三方面的敏 感度最大的是换乘次数，其次是出行耗时，最后是出行费用。 , 417L S V  f , } f 3 2 , 156L , 0036 S min{ , f 1 S , 231L :( S → 3676 )； 0087 , 2210 S , 1784 S → 0485 , S S 3186 S ：( 021L , 0088 S S )； 1557 , 167L 或 217L :( 308L 460L ) 对于问题一，仅考虑公交车线路，根据公交乘客出行心理，建立了一个以换 乘次数最少为首要目标，站点数目最少为第二目标，出行费用最少为第三目标的 多目标规划模型: ，并设计搜索算法，通过编写 C ++程序对最优 → 1828 值进行实现，得到了给出的六对始终点的最优线路分别为： 3359 S ： ( 436L , 097L , 0427 S )； , , 0148 084L S , 189L 对于问题二，相对于问题一，需要多考虑一种出行方式，但其解题思想是一 致的。因此可以基于求解问题一的思想，将所增加的出行方式——地铁，列入考 虑的范围，同样建立了一个多目标规划模型。通过对问题一求解算法进行改进， 编写 C++程序得出题目所给出的六对始终点的最优线路分别为： 3359 S ： ( 436L , 27D , 36D , 3676 , 1784 对于问题三，考虑到现实生活中，人们在转车时，并不是下车直接在下车的 站点处转车，往往需要步行一小段距离到附近的站点取转车，因此把站点之间的 步行时间也纳入考虑范围，建立了基于出行耗费时间最少为目标的单目标规划模 型： S → 1828 S )； 0087 S → 3676 , 167L 或 217L :( 0087 → 0481 S 1919 )； S S S )   T 3 T 2 min( T 1  。 T 最后还对模型和算法进行了评价和改进。 关键词：多目标规划 C ++ 搜索算法 1
    1. 问题的提出 我国人民翘首企盼的第 29 届奥运会明年 8 月将在北京举行，届时有大量观 众到现场观看奥运比赛，其中大部分人将会乘坐公共交通工具（简称公交，包括 公汽、地铁等）出行。这些年来，城市的公交系统有了很大发展，北京市的公交 线路已达 800 条以上，使得公众的出行更加通畅、便利，但同时也面临多条线路 的选择问题。针对市场需求，某公司准备研制开发一个解决公交线路选择问题的 自主查询计算机系统。 要解决的问题： 1. 仅考虑公汽线路，给出任意两公汽站点之间线路选择问题的一般数学模 型与算法。并根据附录数据，利用建立的模型与算法，求出给定的六对 公交站点的最佳路线。 2. 同时考虑公汽与地铁线路，解决以上问题。 3. 假设又知道所有站点之间的步行时间，请你给出任意两站点之间线路选 择问题的数学模型。 2.模型的假设 1.公交车以一定的速度行驶，在行驶的过程中没有意外发生。 2.相邻站点的平均行驶时间为定值，换乘耗时也是定值。 3. 3.符号的说明 )r P 。  P 2   in 表示每一种换乘方式的换乘次数。 1. S 为站点集合。 2. R 为公交线路集合。 3. ( rP 为目标的优先级 1 P 4. n 表示换乘的次数。 5. 6. it 表示每种换乘方式所耗费的平均换乘时间。 7. 8. 9. 10. 11. ijb 为一个 0、1 变量，当两个站点在同一条路线上时为 1，否则为 0。 12. h 为公交车不同线路之间换乘所发生的步行次数。 13. il 步行换线所经过的站点数。 ijc 表示从地铁站 i 到地铁站 j 经过的地铁站点数。 ijd 表示从站点 i 到站点 j 的直达站点数。 ijp 为一个 0、1 变量，当计价是单一票价时为 0，是分段计价时为 1。 ija 为一个 0、1 变量，当乘客有乘坐地铁时为 1，否则为 0。 4.问题的分析 一个公交网络系统有许多不同的公交线路，且每条线路上分布有若干个上 下乘客的站点，求公交线路的选择问题就等价于求从一点到另一点的最短路径问 题，但是公交线路的最短路径的意义与道路网络中的最短路径是不同的，道路网 络中的最短路径就只要找出两点之间距离为最短即可，而在公交网络中，乘客不 会为了寻找距离最短而随意换车，在很多情况下，换乘另一趟车需要步行到另一 2
    个站台，这就有一段的步行距离的代价，而且站台等车也是消费时间的，所以对 于乘客来说，最短路径的意义并不在于路程的最短，而是在于换乘的次数最少。 5.模型的建立与求解 问题一： 5.1.1 模型的建立： 公交线路的选择受到多方面的影响：换乘次数、出行距离、出行耗时和出行 费用。由于已经假设了相邻公汽站平均行驶时间为 3 分钟，所以出行距离和耗时 的考虑可综合到站点数目的考虑上。途径站点数越少，则可理解为出行距离越短、 耗时越少。这样就可用换乘次数、站点数目和出行费用这三个指标来决定线路的 选择，显然，问题属于一个多目标规划问题。文献[1]对公交乘客的出行心理进 行了研究，其结果表明，大部分人考虑出行路径选择的因素依次是换乘次数、站 点数目、出行费用。所以可以考虑通过给目标赋予优先级来得到一个综合指标 z ， 最后以该综合指标来来选择线路。 假设 ( , , i m n k j 表示从起点 i 到终点 j 的换乘站点集合，那么从起点 i 到终点 , ) j 所经过的站点数为： im d 出行费用为：[ 根据以上的分析，得到： d  d im 20  mn  ； d kj  p im 1]     [ d kj 20  p kj  1] 换乘次数最少的目标函数为： 1 min { } n 站点数目最少的目标函数为： 2 min( d    出行费用最少的目标函数为： 3 min   im d  im  20  f f  f  d mn   p im     1  d kj )    d kj 20     p kj  1       可以建立以下多目标规划数学模型： f f 2, 3 } ij min{ , f V  1 0 86 d       0,1 p  ij  , , , , f f j i   , , , , f j i f  1 2 1 2 . . s t , f n  3 , , f n d 3 0 ij  Z 5.1.2 模型的求解： min z P f   1 根据以上模型，设计了如下算法： P 2 P 3     f f 1 2 3 (1) ：输入乘车的起始站点 A 和目的站点 B 。 (2) ：搜索公交数据矩阵，经过起始站点A的公交线路存为 ( )X i ⋯ ，m ，m 为正整数)，经过目的站点B的公交线路存为 ( )Y j n 为正整数 ) 。 (i =l，2，3， ( j =1，2，3，⋯，n ， (3) ：判断是否有 ( ) X i  ，将满足条件的存入 Z 。若 Z  1，则公交线路 ( )X i ( ) Y j 即 ( )Y j 为从站点A到站点B的直达最优线路，输出结果并结束运算;否则继续算法。 (4) ：搜索公交数据矩阵，将公交线路 ( )X i 所包含的公交站点存为公交换乘 矩阵 (O i ， )u (u  l，2，3，⋯ ， g ， g 为正整数 ) ，公交线路 ( )Y j 所包含的站点 3
    存为公交换乘矩阵 (P j ， )(v v  l，2，3，⋯ ， h ， h 为正整数 ) 。 (5) ：判断是否有 (O i ， )u ＝ (P j , )v ，将满足条件的存入W ，若W  1，则站 点 (O i ， )u 即 (P j , )v 为从站点A到站点B的一次换乘站点，公交线路 ( )X i 、 ( )Y j 为 换乘一次的最优路线，输出结果并结束运算；否则继续算法。 (6) ：搜索公交数据库，将经过站点 (O i , )u 的公交线路存为  R k ( k ＝1，2，3， t  1，2，3，⋯ , g ， ⋯ ，P ，P 为正整数)，公交线路 ( )R k 所包含的站点 (G k , )(t g 为正整数 ) 扩充到公交换乘矩阵 (O i ， )u 中。 (7) ：判断是否有 (G k , )t = (P j , )v ，将满足条件的存入W ，若W  1，则站点 (G k ， )t 即 (P j , )v 为从站点 A 到站点 B 的二次换乘站点，公交线路 ( )X i 、 ( )R k 、 ( )Y j 为换乘二次的最优路线，输出结果并结束运算；否则继续算法。 (8) ：设定换乘次数的上界 N ．然后可在不大于 N 次换乘的某次循环中找到 可行路径．若可行路径有多条，考虑综合因素最高的为最优路径并输出。 根据题目给的六对起始站点，根据上述算法通过计算得到以下结果： 从站点S3359到S1828只需换乘一次，最佳线路为：从S3359乘坐下行方向的 L436号线到S1784换乘下行方向的L167或者L217号线即可到达S1828。 从站点S0087到S3676需要换乘两次，最佳路线：从S0087乘坐下行方向的L021 号线到S0088换乘环行的L231号线，然后再到S0427换乘上行的L097号线即可到达 S3676。 从站点S0148到S0485需要换乘两次，最佳路线为：从S0148乘坐上行的L308 号线到S0036换乘上行的L156号线，然后再到S2210换乘下行的L417号线即可到达 S0485。 从站点S1557到S0481需要换乘两次，最佳路线为：从S1557乘坐下行的L084 号线到S1919换乘下行的L189号线，然后再到S3186换乘下行的L460号线即可到达 S0481。 问题二： 5.2.1 模型的建立： 问题二需要比问题一多考虑两条地铁线，本质上与问题一是一致的，线路的 选择的一般指标都是换乘次数、耗费时间和出行费用，所不同的是因多了地铁线 而需要在问题一上面多考虑一种出行方式。考虑到从起点 i 到终点 j ，既可以通 过公交换乘到达，又可以通过换乘地铁（乘坐地铁需要耗费步行时间）到达，所 以在两种方式所换乘的次数相同时，乘客会偏向于采用公交换乘。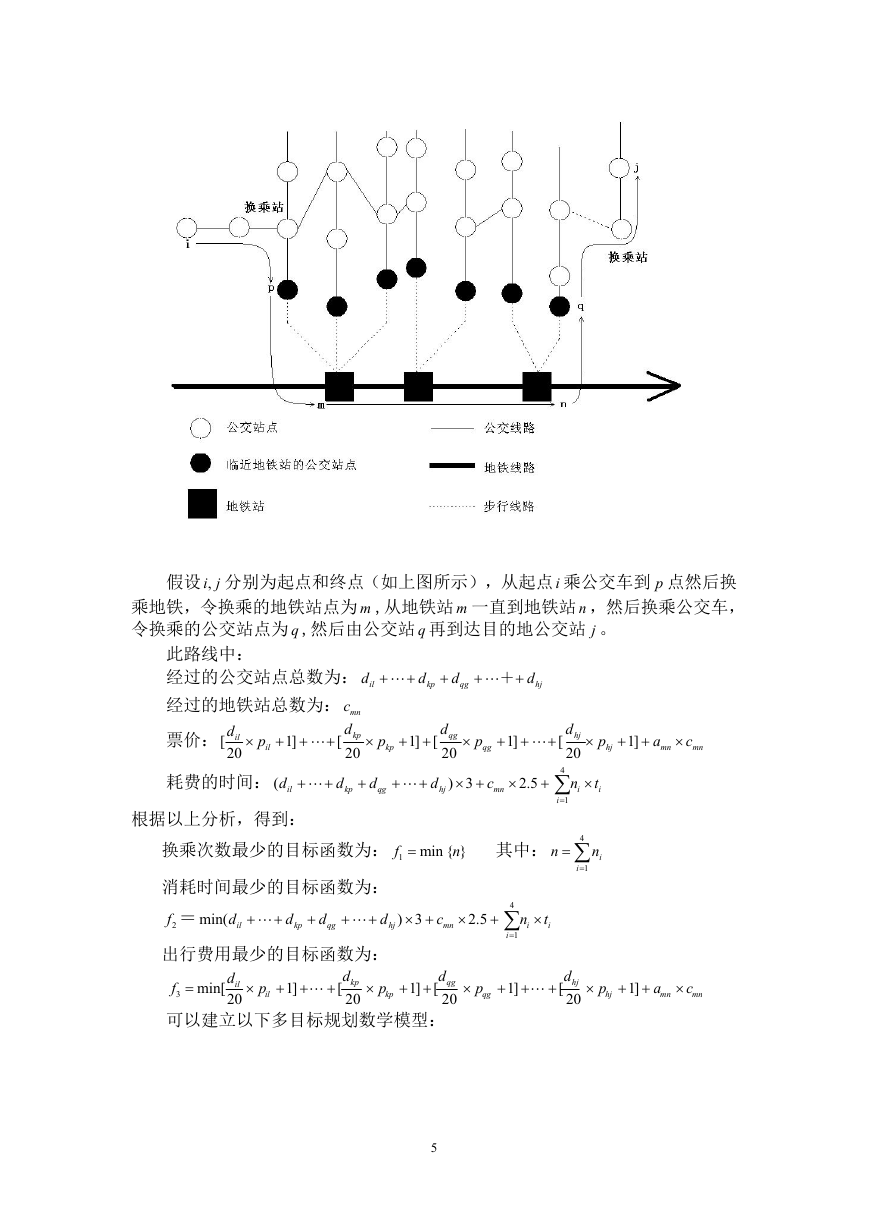公交线路与地 铁线路之间的关系可见下图： 4
    假设 ,i j 分别为起点和终点（如上图所示），从起点 i 乘公交车到 p 点然后换 乘地铁，令换乘的地铁站点为 m ,从地铁站 m 一直到地铁站 n ，然后换乘公交车， 令换乘的公交站点为 q ,然后由公交站 q 再到达目的地公交站 j 。 此路线中： d 经过的公交站点总数为： il 经过的地铁站总数为： mnc d kp 20 票价：[ 1]   d il 20  p il    [    d kp  d qg  ＋  d hj p kp 1]   [ p qg 1]     耗费的时间： ( d il    d kp  d qg    d 根据以上分析，得到：  d qg 20 ) 3   hj c mn  2.5   [ d hj 20  n i 4 i 1  p hj 1]   a mn  c mn t i 换乘次数最少的目标函数为： 1 min { } n  f 其中： n 4   i 1  n i 消耗时间最少的目标函数为： 2f ＝ min( d il    d kp  d qg    d hj ) 3   c mn  2.5  4  n i t i i 1  出行费用最少的目标函数为： f 3 min[  d il 20  p il 1]     [ d kp 20  p kp 1]   [ d qg 20 可以建立以下多目标规划数学模型：  p qg 1]     [ d hj 20  p hj 1]   a mn  c mn 5
    ij min{ , V f  1 0 86 d       0,1 p  ij     0,1 a ij , , , , f f i j , , , , i f f j 1 4        n  ( n i i 1  1 2 2 i . . s t f f 2, 3 } , f n c 3 ij , f n d 3 , , ij 0  Z   1,2,3,4) 5.2.2 模型的求解： P 2  1 2 f f     P 3 min z P f  1 根据以上的分析，设计如下算法： 步骤1：输入乘车的起始站点 A 和目的站点 B 。 步骤2：搜索公交数据矩阵，经过起始站点A的公交线路存为 ( )X i 3 ⋯ ，m ，m 为正整数 ) ，经过目的站点B的公交线路存为 ( )Y i n 为正整数 ) 。 (i =l，2，3， ( j =1，2，3，⋯，n ， 步骤3：判断是否有 ( )X i ＝ ( )Y i ，将满足条件的存入 Z 。若 Z  1，则公交线 路 ( )X i 即 ( )Y i 为从站点A到站点B的直达最优线路，输出结果并结束运算;否则继 续算法。 步骤4：把地铁对应的公交站点存为 ( )C k ,判断A和B是否都属于矩阵 ( )C k ，若 两者都属于矩阵 ( )C k ，则A到B有可通过直接乘坐地铁直达的最优线路，输出结果 并结束运算；否则继续算法。 步骤5：搜索公交数据矩阵，将公交线路 ( )X i 所包含的公交站点存为公交换 乘矩阵 (O i , )u (u  1,2,3,…, g , g 为正整数),公交线路 ( )Y i 所包含的站点存为 公交换乘矩阵 (P j , )(v v ＝1,2,3,…, v , v 为正整数 ) 。 步骤6：判断是否有 (O i ， ) v j ， )v ，将满足条件的存入W ，若W  1，则站 点 (O i , )u 即 (P j , )v 为从站点 A 到站点 B 的一次换乘站点，公交线路 ( )X i 、 ( )Y i 为 换乘一次的最优路线，输出结果并结束运算；否则继续算法。 ( 步骤7：判断A或B是否有一个属于矩阵 ( )C k ，如果有，再判断 ( )X i , ( )Y i 是否 有一个等于 ( )C k ，如果有，则A到B有通过换乘一次地铁的最优线路，k 为换乘站 点，输出结果并结束运算；否则继续算法。 步骤8：如此类推，设定换乘次数的上界 N ．然后可在不大于 N 次换乘的某 次循环中找到可行路径．若可行路径有多条，考虑综合因素最高的为最优路径并 输出。 问题三： 5.3.1 模型的建立： 通过对以上模型和算法进行分析可以发现只有当不同线路之间具有公共站 点时才能够进行换乘，这样算得的结果有时与实际情况并不相符合，例如在实际 出行时，人们很有可能会先步行一小段距离到附近的站点换乘，而不是在原地换 乘。所以线路的选择还必须考虑到步行的时间。 基于上述思想，那么人们从起点 i 到终点 j 所耗费的时间包括三方面：乘车 6
    2 3 T  最小。 耗费的时间 ( 1)T 、换乘耗费的时间 ( 2)T 和步行耗费的时间 ( 3)T 。现在需要解决的 就是求出一条线路使得 1 T T  (1) 乘车耗费的时间 ( 1)T 由问题二的模型可知： 从起点 i 到终点 j 所经过的公交站点数为： il d 经过的地铁站点数为： mnc 所以乘车耗费的时间为： 1 ( T  (2) 换乘耗费的时间 ( 2)T 由于从起点 i 到终点 j 可能要进行换乘，而且换乘的方式有多种：公交换公 ) 3   ＋ 2.5               d d d d d d d c mn qg qg kp kp hj hj il 交、公交换地铁、地铁换公交和地铁换地铁。每一种换乘方式所耗费的时间不同， n 因此要同时考虑到四种换乘方式所需的时间。公交换公交需要 1 n 交换地铁需要 3 t 的时间，地铁换地铁需要 4 n t 的时间，公 t 3 4 i 的时间，所以总共耗费的换乘时间为： t 的时间，地铁换公交需要 2 n 4  n i T 2  2 t i i 1  (3)步行耗费的时间 ( 3)T 由题目可知步行换乘有四种方式：从公交站步行到公交站、从公交站步行到 地铁站、从地铁站步行到公交站、从地铁站步行到地铁站。由常识可知，人们从 ija4 的时 起点到终点最多只会乘坐一次地铁，所以从公交站步行到地铁站需要 ija 的时间。再假设公交换乘公交时发生了 h 间，从地铁站步行到公交站也需要 4 次步行，每次步行到相隔l 个站的公交站点换乘，那么就有从公交站步行到站需 要  的时间。而地铁步行到地铁则需要 2 2 l i h i 1   a ij  的时间。所以总共耗费的步 b ij T 行时间为： 3 8   a ij  h  i 1  2 2    l i a ij  b ij 综上所述，可得到如下优化模型： T  min( T 1  T 2  T 3 ) d    d hj ) 3   c mn  2.5 qg 2    l a ij  b ij i i i h ij il t kp 1  a d       2 n i  ( d 4   1 i  Z  T  1   T  2     8 T   3  . . s t h d c n l  , , , ,  i ij  , , 0 h d c  ij ij      0,1 0,1 , a b    ij ij   ) 1,2 0( h i l    i  , 1,2,3,4) 0( i n t    i 6.模型的评价 ij i i 6.1. 模型的优点： 1. 2. 7
    6.2. 模型的缺点： 3. 1. 2. 7.模型的改进 对于上述模型结果的实现，是基于算法搜索的方法得到的，算法要求对所有 的公交线路进行搜索，然后得出最优线路。由于题目给出的公交线路很多，再加 上地铁线路，如果对每一个站点都进行测试，寻找可行线路，那么站点和对应线 路的换乘矩阵将会很庞大，这样会加大搜索的难度和时间复杂度，基于此，考虑 对上述的算法进行改进。 考虑到乘客出行的一个约束条件——距离，则需要采用基于最短路径的公交 换乘方案，即将换乘点的搜索范围缩小，在公交网络上求出从起始点到目标点的 最短路径，将最短路径上的站点作为可能的换乘点，这样就大幅度的减少了换乘 站点的搜索范围，减少了公交站点换乘矩阵，提高了公交线路的搜索速度。由于 时间的关系，具体的算法没有给出。 8.参考文献 [1] 杨新苗，王 炜，马文腾. 基于 GIS 的公交乘客出行路径选择模型[J]. 东南 [2] 扈 震，张发勇，刘书良. 城市公交换乘数据模型研究及算法实现. 电信网 大学学报，2000，30(6)：88~91. 技术，2007.4 第 4 期 [3] 苏爱华，施法中. 公交网络换乘问题的一种实现. 工程图学学报，2005 第 4 期 S1828 附表 1： S3359 换乘点 L436 下行 L167 下行 S1784 L436 下行 L167 下行 S1241 L469 上行 L167 下行 S0519 L436 下行 L217 下行 S1241 L436 下行 L217 下行 S3695 L436 上行 L217 下行 S1784 L436 下行 L217 下行 S2606 L469 上行 L217 下行 S3192 L469 上行 L217 下行 S0304 L469 上行 L217 下行 S0727 L469 上行 L217 下行 S2364 附表 2： S0087 L021 上行 L231 环行 S3676 L097 上行 9.附录 站点数 32 34 44 34 36 32 40 44 44 44 44 票价 3 3 4 3 3 3 3 3 3 3 3 耗时 101 107 137 107 113 101 125 137 137 137 137 站点数 14 票价 3 耗时 52 换乘点 S0630 S0427 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料