最短路径算法实验报告.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.27M 资料格式：pdf 举报版权申诉

u013753440-8877951-4744300845365860749.pdf-第1页.png

第1页 / 共6页

u013753440-8877951-4744300845365860749.pdf-第2页.png

第2页 / 共6页

u013753440-8877951-4744300845365860749.pdf-第3页.png

第3页 / 共6页

u013753440-8877951-4744300845365860749.pdf-第4页.png

第4页 / 共6页

u013753440-8877951-4744300845365860749.pdf-第5页.png

第5页 / 共6页

u013753440-8877951-4744300845365860749.pdf-第6页.png

第6页 / 共6页

文本预览

端间最短路径 Dijkstra 算法实验报告一、实验目的本次实验要求利用 MATLAB 分别实现 Dijkstra 算法和 Floyd 算法，可对输入的邻接距离矩阵计算图中任意两点间的最短距离矩阵和路由矩阵，且能查询任意两点间的最短距离和路由。二、实验原理 D 算法的每个端点 iv 的标号为 ( i l ，其中 i表示 1v 到 iv 的距离，而l 为端点 , ) 是 1v 到 iv 最短路径的最后一个端点。图G （，）的每一边上有一个权 ( ) 0 w e  。 V E D0：初始 (0) X v ，记 1 1{ } 0  ，设 1v 的标号为 1( ,1) 。 D1：对任一边 i l ( , )  反圈  ( X ( k ) )( v i  X ( k ) , v l  X ( k ) ) ，计算 i 中选一边，设为 i ( , 0 l 0 )( v i 0  X ( k ) , v l 0  X ( k ) ) 。使  i 0  w i l 0 0    l i 0 0  ，并且 i lw 0 0 0lv 的标号为 i（）。 0,l 0 ilw 的值。在 w il (  i min k ( ) i l ( , )  ( X ) )kX ) ( (  ，并令 ) D2：当出现下面情况之一时停止。 1） jv X ；2） )k ( jv X 但 )k ( kX ( ( )  ）三、实验内容用 MATLAB 仿真工具实现 D 算法和 F 算法：给定图 G 及其边 ( , ) j 的权 i jw i , (1   i n ,1   ，可用 D 算法和 F 算法分别求出其各个端点之间的最小距 j n ) 离以及路由。四、采用的语言 MatLab 语言源代码： ○1 核心代码 function [distance,path] = Dijk( W,st,e ) %DIJK Summary of this function goes here

% W 权值矩阵 st 搜索的起点 e 搜索的终点 n=length(W);%节点数 D = W(st,:); visit= ones(1:n); visit(st)=0; parent = zeros(1,n);%记录每个节点的上一个节点 path =[]; for i=1:n-1 temp = []; %从起点出发，找最短距离的下一个点，每次不会重复原来的轨迹，设置 visit 判断节点是否访问 for j=1:n if visit(j) temp =[temp D(j)]; temp =[temp inf]; else end end [value,index] = min(temp); visit(index) = 0; %更新如果经过 index 节点，从起点到每个节点的路径长度更小，则更新，记录前趋节点，方便后面回溯循迹 for k=1:n if D(k)>D(index)+W(index,k) D(k) = D(index)+W(index,k); parent(k) = index; end end end distance = D(e);%最短距离 %回溯法从尾部往前寻找搜索路径 t = e; while t~=st && t>0 path =[t,path]; p=parent(t);t=p; end path =[st,path];%最短路径 end

○2 验证算法的代码，改变输入的矩阵就可以得到不同的结果 W=[0 100 100 1.2 9.2 100 0.5 100 0 100 5 100 3.1 2 100 100 0 100 100 4 1.5 1.2 5 100 0 6.7 100 1.7 9.2 100 100 6.7 0 15.6 9.7 100 3.1 4 100 15.6 0 100 0.5 2 1.5 1.7 9.7 100 0]; n=length(W); for i=1:n for j=1:n [distance,path]=Dijk(W,i,j); m=length(path); W7(i,j)=distance; if(i==j) R7(i,j)=0; else R7(i,j)=path(m-1); end end end 五、数据结构 1. 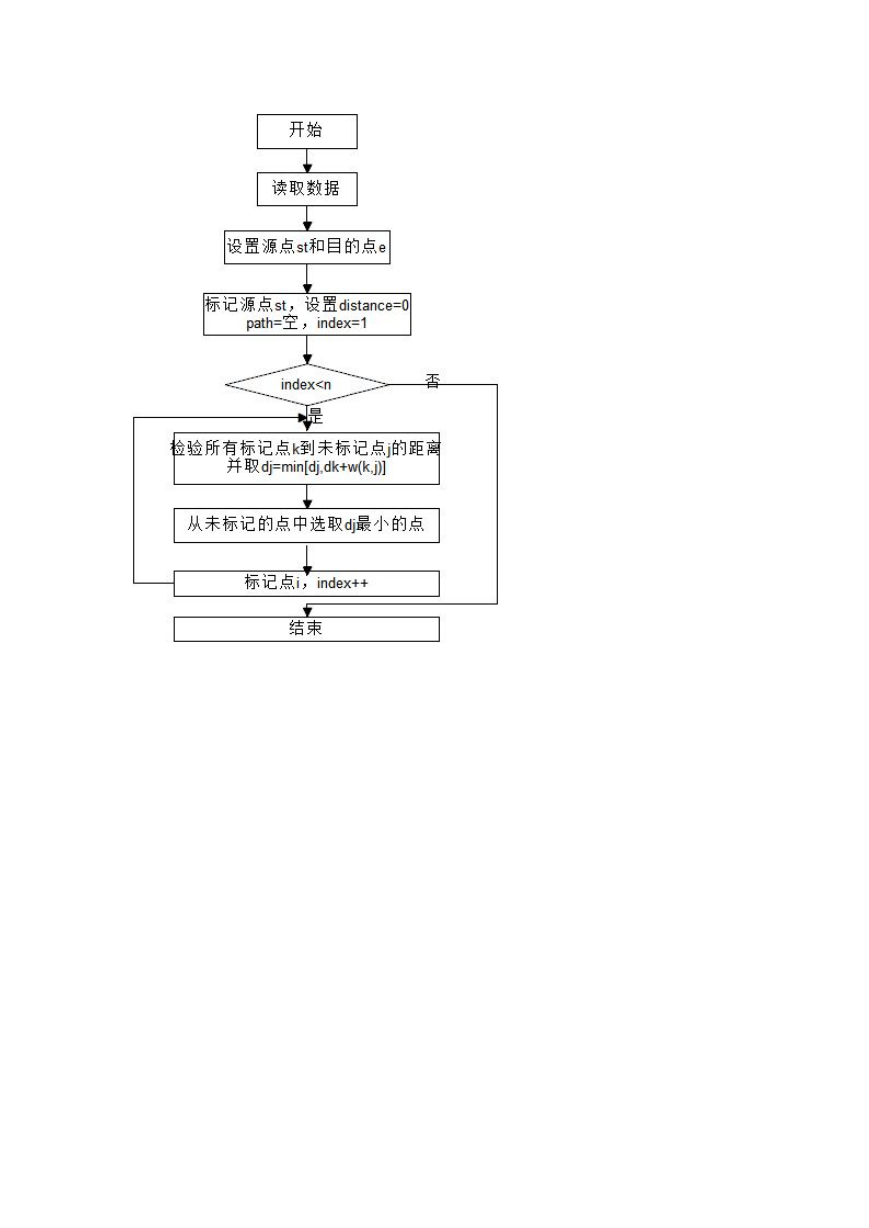Dijkstra 算法（主要函数） [distance,path] = Dijk( W,st,e )； W 权值矩阵 st 搜索的起点 e 搜索的终点 distance 最短距离 path 经过的路由 2.算法的流程图

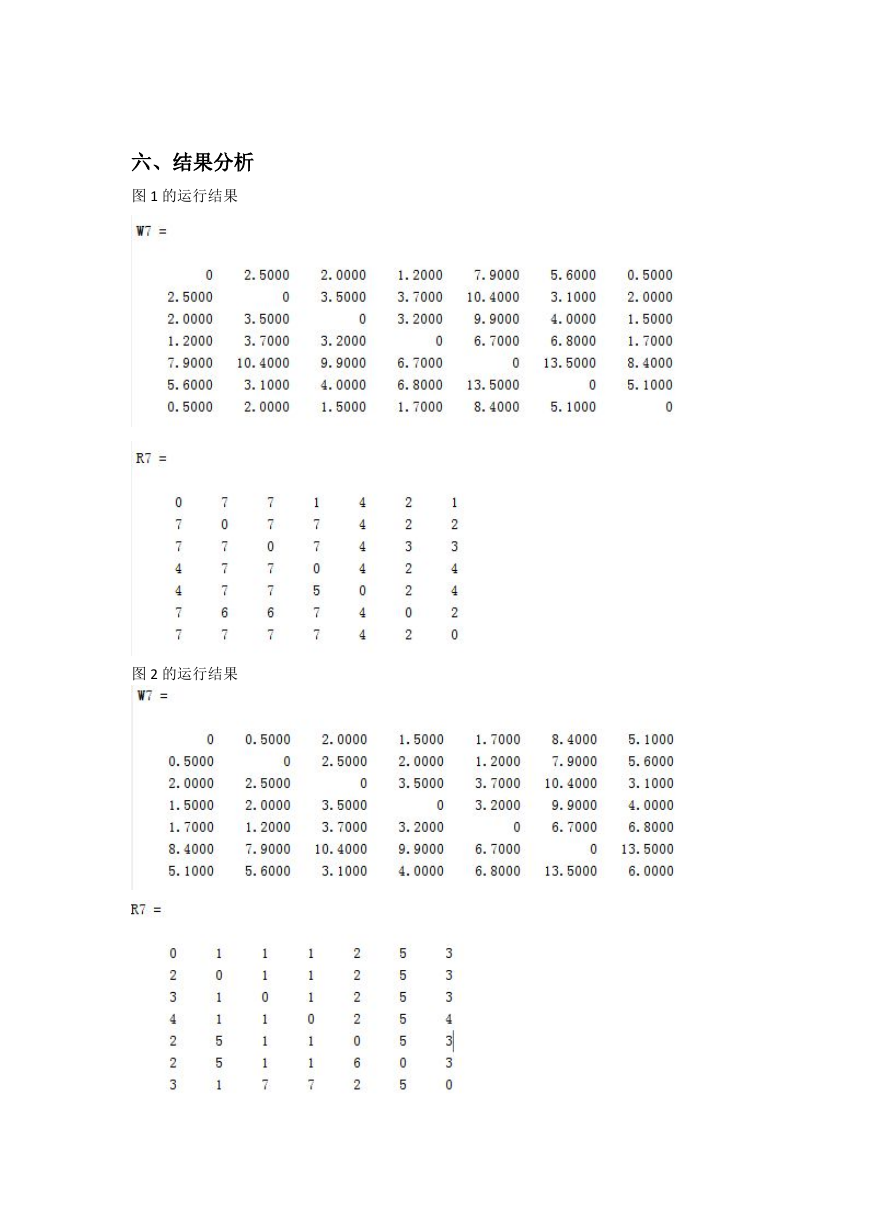
六、结果分析图 1 的运行结果图 2 的运行结果

最短距离可以从最短距离矩阵的 W7(i,j)中直接得出,相应的路由则可以通过在路由矩阵 R7(i,j)中查找得出. 单一指定俩端之间的最小距离和经过的路由可以通过函数[distance,path] = Dijk( W,st,e )得到。对图 1，分别以端点对 V4 和 V6, V3 和 V4 为例，V4→ V6 最短距离为 6.8，经过的路由为 4→7→2→6;V3→V4 最短距离为 3.2，路由为 3→7→4；对图 2，分别以端点对 V1 和 V7，V3 和 V5，V1 和 V6 为例，V1→ V7 最短距离为 5.1 ，经过的路由为 1→3→7;V3→V5 最短距离为 3.7 ，经过的路由为 3→1→2→5；V1→V6 最短距离为 8.4，路由为 1→2→5→6；七、遇到的问题及解决方法开始输出的不是矩阵，只是单一地通过函数[distance,path] = Dijk( W,st,e )求出最小距离和经过的路由，最后利用 for 循环成功地输出矩阵。八、实验心得通过本次实验我对最短路径 Dijkstra 算法有了深入地了解，同时对 MatLab 编程语言更加熟悉。本次实验让我受益匪浅。

分享到：

赞收藏

资料库

最短路径算法实验报告.pdf

相关推荐

开发技术

热门标签

最新资料