logo资料库

基于深度学习语音分离技术的研究现状与进展_刘文举.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.15M 资料格式：pdf 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    第 42 卷 第 6 期 2016 年 6 月 自 动 化 学 报 ACTA AUTOMATICA SINICA Vol. 42, No. 6 June, 2016 基于深度学习语音分离技术的研究现状与进展 刘文举 1 聂 帅 1 梁 山 1 张学良 2 摘 要 现阶段, 语音交互技术日益在现实生活中得到广泛的应用, 然而, 由于干扰的存在, 现实环境中的语音交互技术远没 有达到令人满意的程度. 针对加性噪音的语音分离技术是提高语音交互性能的有效途径, 几十年来, 全世界范围内的许多研究 者为此投入了巨大的努力, 提出了很多实用的方法. 特别是近年来, 由于深度学习研究的兴起, 基于深度学习的语音分离技术 日益得到了广泛关注和重视, 显露出了相当光明的应用前景, 逐渐成为语音分离中一个新的研究趋势. 目前已有很多基于深度 学习的语音分离方法被提出, 但是, 对于深度学习语音分离技术一直以来都缺乏一个系统的分析和总结, 不同方法之间的联系 和区分也很少被研究. 针对这个问题, 本文试图对语音分离的主要流程和整体框架进行细致的分析和总结, 从特征、模型以及 目标三个方面对现有的前沿研究进展进行全面而深入的综述, 最后对语音分离技术进行展望. 关键词 神经网络, 语音分离, 计算听觉场景分析, 机器学习 引用格式 刘文举, 聂帅, 梁山, 张学良. 基于深度学习语音分离技术的研究现状与进展. 自动化学报, 2016, 42(6): 819−833 DOI 10.16383/j.aas.2016.c150734 Deep Learning Based Speech Separation Technology and Its Developments LIU Wen-Ju1 NIE Shuai1 LIANG Shan1 ZHANG Xue-Liang2 Abstract Nowadays, speech interaction technology has been widely used in our daily life. However, due to the interfer- ences, the performances of speech interaction systems in real-world environments are far from being satisfactory. Speech separation technology has been proven to be an effective way to improve the performance of speech interaction in noisy environments. To this end, decades of efforts have been devoted to speech separation. There have been many methods proposed and a lot of success achieved. Especially with the rise of deep learning, deep learning-based speech separation has been proposed and extensively studied, which has been shown considerable promise and become a main research line. So far, there have been many deep learning-based speech separation methods proposed. However, there is little systematic analysis and summary on the deep learning-based speech separation technology. We try to give a detail analysis and summary on the general procedures and components of speech separation in this regard. Moreover, we survey a wide range of supervised speech separation techniques from three aspects: 1) features, 2) targets, 3) models. And finally we give some views on its developments. Key words Neural network, speech separation, computational auditory scene analysis, machine learning Citation Liu Wen-Ju, Nie Shuai, Liang Shan, Zhang Xue-Liang. Deep learning based speech separation technology and its developments. Acta Automatica Sinica, 2016, 42(6): 819−833 现实环境中, 感兴趣的语音信号通常会被噪音 干扰, 严重损害了语音的可懂度, 降低了语音识别的 性能. 针对噪音, 前端语音分离技术是最常用的方法 之一. 一个好的前端语音分离模块能够极大地提高 语音的可懂度和自动语音识别系统的识别性能[1−6]. 然而, 在真实环境中, 语音分离技术的性能远没有达 收稿日期 2015-11-04 录用日期 2016-04-01 Manuscript received November 4, 2015; accepted April 1, 2016 国家自然科学基金 (61573357, 61503382, 61403370, 61273267, 911 20303, 61365006) 资助 Supported by National Natural Science Foundation of China (61573357, 61503382, 61403370, 61273267, 91120303, 61365006) 本文责任编委 柯登峰 Recommended by Associate Editor KE Deng-Feng 1. 中国科学院自动化研究所模式识别国家重点实验室 北京 100190 2. 内蒙古大学计算机系 呼和浩特 010021 1. National Laboratory of Patten Recognition, Institute of Automation, Chinese Academy of Sciences, Beijing 100190 2. College of Computer Science, Inner Mongolia University, Huhhot 010021 到令人满意的程度, 特别是在非平稳噪音和单声道 的情况下, 语音分离依然面临着巨大的挑战. 本文重 点探讨单声道条件下语音分离技术. 几十年来, 单声道条件下的语音分离问题被广 泛地研究. 从信号处理的角度来看, 许多方法提出 估计噪音的功率谱或者理想维纳滤波器, 比如谱减 法[7] 和维纳滤波法[8−9]. 其中维纳滤波是最小均方 误差意义下分离纯净语音的最优滤波器[9]. 在假定 语音和噪音的先验分布的条件下, 给定带噪语音, 它 能推断出语音的谱系数. 基于信号处理的方法通常 假设噪音是平稳的或者是慢变的[10]. 在满足假设条 件的情况下, 这些方法能够取得比较好的分离性能. 然而, 在现实情况下, 这些假设条件通常很难满足, 其分离性能会严重地下降, 特别在低信噪比条件下, 这些方法通常会失效[9]. 相比于信号处理的方法, 基 于模型的方法利用混合前的纯净信号分别构建语音
    820 自 动 化 学 报 42 卷 和噪音的模型, 例如文献 [11−13], 在低信噪比的情 况下取得了重要的性能提升. 但是基于模型的方法 严重依赖于事先训练的语音和噪音模型, 对于不匹 配的语音或者噪音, 其性能通常会严重下降. 在基于 模型的语音分离方法中, 非负矩阵分解是常用的建 模方法, 它能挖掘非负数据中的局部基表示, 目前已 被广泛地应用到语音分离中[14−15]. 然而非负矩阵分 解是一个浅层的线性模型, 很难挖掘语音数据中复 杂的非线性结构. 另外, 非负矩阵分解的推断过程非 常费时, 很难应用到实际应用中. 计算听觉场景分析 是另一个重要的语音分离技术, 它试图模拟人耳对 声音的处理过程来解决语音分离问题[16]. 计算听觉 场景分析的基本计算目标是估计一个理想二值掩蔽, 根据人耳的听觉掩蔽来实现语音的分离. 相对于其 他语音分离的方法, 计算听觉场景分析对噪音没有 任何假设, 具有更好的泛化性能. 然而, 计算听觉场 景分析严重依赖于语音的基音检测, 在噪音的干扰 下, 语音的基音检测是非常困难的. 另外, 由于缺乏 谐波结构, 计算听觉场景分析很难处理语音中的清 音成分. 语音分离旨在从被干扰的语音信号中分离出有 用的信号, 这个过程能够很自然地表达成一个监督 性学习问题[17−20]. 一个典型的监督性语音分离系统 通常通过监督性学习算法, 例如深度神经网络, 学习 一个从带噪特征到分离目标 (例如理想掩蔽或者感 兴趣语音的幅度谱) 的映射函数[17]. 最近, 监督性语 音分离得到了研究者的广泛关注, 取得了巨大的成 功. 作为一个新的研究趋势, 相对于传统的语音增强 技术[9], 监督性语音分离不需要声源的空间方位信 息, 且对噪音的统计特性没有任何限制, 在单声道, 非平稳噪声和低信噪比的条件下显示出了明显的优 势和相当光明的研究前景[21−23]. 从监督性学习的角度来看, 监督性语音分离主 要涉及特征、模型和目标三个方面的内容. 语音分 离系统通常利用时频分解技术从带噪语音中提取 时频域特征, 常用的时频分解技术有短时傅里叶 变换 (Short-time Fourier transform, STFT)[24] 和 Gammatone 听觉滤波模型[25]. 相应地, 语音分离 特征可以分为傅里叶变换域特征和 Gammatone 滤 波变换域特征. Wang 和 Chen 等在文献 [26−27] 中系统地总结和分析了 Gammatone 滤波变换域 特征, 提出了一些列组合特征和多分辨率特征. 而 Mohammadiha、Xu、Weninger、Le Roux、Huang 等使用傅里叶幅度谱或者傅里叶对数幅度谱作为 语音分离的输入特征[14, 18, 20, 23, 28−29]. 从建模单元 来区分, 语音分离的特征又可分为时频单元级别的 特征和帧级别的特征. 时频单元级别的特征从一 个时频单元的信号中提取, 帧级别的特征从一帧信 号中提取, 早期, 由于模型学习能力的限制, 监督 性语音分离方法通常对时频单元进行建模, 因此使 用时频单元级别的特征, 例如文献 [1] 和文献 [30− 34]. 现阶段, 监督性语音分离主要使用帧级别的 特征[17−21, 23, 35−36]. 监督性语音分离系统的学习模 型主要分为浅层模型和深层模型. 早期的监督性 语音分离系统主要使用浅层模型, 比如高斯混合 模型 (Gaussian mixture model, GMM)[1]、支持向 量机 (Support vector machine, SVM)[26, 30, 32] 和 非负矩阵分解 (Nonnegative matrix factorization, NMF)[14]. 然而, 语音信号具有明显的时空结构和 非线性关系, 浅层结构在挖掘这些非线性结构信息 的能力上非常有限. 而深层模型由于其多层次的非 线性处理结构, 非常擅长于挖掘数据中的结构信 息, 能够自动提取抽象化的特征表示, 因此, 近年 来, 深层模型被广泛地应用到语音和图像处理中, 并取得了巨大的成功[37]. 以深度神经网络 (Deep neural network, DNN) 为代表的深度学习[37] 是深 层模型的典型代表, 目前已被广泛应用到语音分离 中[5, 18, 20, 22, 29, 38−39]. 最近, Le Roux、Hershey 和 Hsu 等将 NMF 扩展成深层结构并应用到语音分 离中, 取得了巨大的性能提升[23, 40−41], 在语音分离 中显示了巨大的研究前景, 日益得到人们的重视. 理想时频掩蔽和目标语音的幅度谱是监督性语音 分离的常用目标, 如果不考虑相位的影响, 利用估 计的掩蔽或者幅度谱能够合成目标语音波形, 实验 证明利用这种方法分离的语音能够显著地抑制噪 音[42−43], 提高语音的可懂度和语音识别系统的性 能[38, 44−49]. 但是, 最近的一些研究显示, 相位信息 对于语音的感知质量是重要的[50]. 为此, 一些语音 分离方法开始关注相位的估计, 并取得了分离性能 的提升[51−52]. 为了将语音的相位信息考虑到语音分 离中, Williamson 等将浮值掩蔽扩展到复数域, 提 出复数域的掩蔽目标, 该目标在基于深度神经网络 的语音分离系统中显著地提高了分离语音的感知质 量[53]. 语音分离作为一个重要的研究领域, 几十年来, 受到国内外研究者的广泛关注和重视. 近年来, 监 督性语音分离技术取得了重要的研究进展, 特别是 深度学习的应用, 极大地促进了语音分离的发展. 然 而, 对监督性语音分离方法一直以来缺乏一个系统 的分析和总结, 尽管有一些综述性的工作被提出, 但 是它们往往局限于其中的一个方面, 例如, Wang 等 在文献 [17] 中侧重于监督性语音分离的目标分析, 而在文献 [26] 中主要比较了监督性语音分离的特征, 并没有一个整体的总结和分析, 同时也没有对这些 工作的相互联系以及区别进行研究. 本文从监督性 语音分离涉及到的特征、模型和目标三个主要方面
    6 期 刘文举等: 基于深度学习语音分离技术的研究现状与进展 821 对语音分离的一般流程和整体框架进行了详细的介 绍、归纳和总结. 以此希望为该领域的研究及应用 提供一个参考. 本文的组织结构如下: 第 1 节概述了语音分离 的主要流程和整体框架; 第 2∼ 5 节分别介绍了语音 分离中的时频分解、特征、目标、模型等关键模块; 最后, 对全文进行了总结和展望, 并从建模单元、目 标和训练模型三个方面对监督性语音分离方法进行 了比较和分析. 1 系统结构 图 1 给出了语音分离的一般性结构框图, 主要 分为 5 个模块: 1) 时频分解, 通过信号处理的方法 (听觉滤波器组或者短时傅里叶变换) 将输入的时域 信号分解成二维的时频信号表示. 2) 特征提取, 提 取帧级别或者时频单元级别的听觉特征, 比如, 短 时傅里叶变换谱 (FFT-magnitude)、短时傅里叶变 换对数谱 (FFT-log)、Amplitude modulation spec- trogram (AMS)、Relative spectral transform and perceptual linear prediction (RASTA-PLP)、Mel- frequency cepstral coefficients (MFCC)、Pitch- based features 以及 Multi-resolution cochleagram (MRCG). 3) 分离目标, 利用估计的分离目标以及 混合信号合成目标语音的波形信号. 针对语音分离 的不同应用特点, 例如针对语音识别, 语音分离在 分离语音的过程中侧重减少语音畸变和尽可能地保 留语音成分. 针对语音通讯, 语音分离侧重于提高 分离语音的可懂度和感知质量. 常用的语音分离目 标主要分为时频掩蔽的目标、目标语音幅度谱估计 的目标和隐式时频掩蔽目标, 时频掩蔽目标训练一 个模型来估计一个理想时频掩蔽, 使得估计的掩蔽 和理想掩蔽尽可能相似; 目标语音幅度谱估计的方 法训练一个模型来估计目标语音的幅度谱, 使得估 计的幅度谱与目标语音的幅度谱尽可能相似; 隐式 时频掩蔽目标将时频掩蔽技术融合到实际应用的模 型中, 用来增强语音特征或估计目标语音, 隐式掩 蔽并不直接估计理想掩蔽, 而是作为中间的一个计 算过程来得到最终学习的目标, 隐式掩蔽作为一个 确定性的计算过程, 并没有参数需要学习, 最终的 目标误差通过隐式掩蔽的传导来更新模型参数. 4) 模型训练, 利用大量的输入输出训练对通过机器学 习算法学习一个从带噪特征到分离目标的映射函 数, 应用于语音分离的学习模型大致可分为浅层模 型 (GMM, SVM, NMF) 和深层模型 (DNN, DSN, CNN, RNN, LSTM, Deep NMF). 5) 波形合成, 利 用估计的分离目标以及混合信号, 通过逆变换 (逆傅 里叶变换或者逆 Gammatone 滤波) 获得目标语音 的波形信号. +∞ −∞ 图 1 监督性语音分离系统的结构框图 Fig. 1 A block diagram of the supervised speech separation system 2 时频分解 时频分解是整个系统的前端处理模块, 通过时 频分解, 输入的一维时域信号能够被分解成二维的 时频信号. 常用的时频分解方法包括短时傅里叶变 换[24] 和 Gammatone 听觉滤波模型[25]. 假 设 w(t) = w(−t) 是 一 个 实 对 称 窗 函 数, X(t, f) 是一维时域信号 x(k) 在第 t 时间帧、第 f 个频段的短时傅里叶变换系数, 则 X(t, f) = x(k)w(k − t) exp(−j2πf k)dk (1) 对应的傅里叶能量幅度谱 px(t, f) 为 px(t, f) = |X(t, f)| (2) 其中, | · | 表示复数域的取模操作. 为了简化符号 表示, 用向量 ppp ∈ RF×1 + 表示时间帧为 t 的幅度 谱, 这里 F 是傅里叶变换的频带数. 短时傅里叶变 换是完备而稳定的[54], 可以通过短时傅里叶逆变换 (Inverse short-time Fourier transform, ISTFT) 从 X(t, f) 精确重构 x(k). 也就是说, 可以通过估计目 标语音的短时傅里叶变换系数来实现语音的分离或 者增强, 用 ˆYs(t, f) 来表示估计的目标语音的短时傅 里叶变换系数, 那么目标语音的波形 ˆs(k) 可以通过 ISTFT 计算 ˆs(k) = +∞ +∞ −∞ −∞ ˆYs(k)w(k − t) exp(j2πf k)dfdk (3) 如果不考虑相位的影响, 语音分离过程可以转 换为目标语音幅度谱的估计问题, 一旦估计出目标
    822 自 动 化 学 报 42 卷 语音的幅度谱 ˆyyys ∈ RF×1 过 ISTFT, 能得到目标语音的估计波形 ˆs(k)[17]. + , 联合混合语音的相位, 通 Gammatone 听 觉 滤 波 使 用 一 组 听 觉 滤 波 器 g(t) 对 输 入 信 号 进 行 滤 波, 得 到 一 组 滤 波 输 出 G(k, f). 滤波器组的冲击响应为 tl−1 exp(−2πbt) cos(2πf t), 0, t ≥ 0 其他 (4) g(t) = 其中, 滤波器阶数 l = 4, b 为等效矩形带宽 (Equiv- alent rectangle bandwidth, ERB), f 为滤波器的 中心频率, Gammatone 滤波器组的中心频率沿对 数频率轴等间隔地分布在 [80 Hz, 5 kHz]. 等效矩形 带宽与中心频率一般满足式 (5) , 可以看出随着中 心频率的增加, 滤波器带宽加宽. ERB(f) = 24.7(0.0043f + 1.0) (5) 对于 4 阶的 Gammatone 滤波器, Patterson 等[25] 给出了带宽的计算公式 b = 1.093ERB(f) (6) 然后, 采用交叠分段的方法, 以 20 ms 为帧长, 10 ms 为偏移量对每一个频率通道的滤波响应做分帧加窗 处理. 得到输入信号的时频域表示, 即时频单元. 在 计算听觉场景分析系统中, 时频单元被认为是处理 的最小单位, 用 T-F 表示. 通过计算时频单元内的 内毛细胞输出 (或者听觉滤波器输出) 能量, 就得到 了听觉谱 (Cochleagram) , 本文用 GF (t, f) 表示时 间帧 t 频率为 f 的时频单元 T-F 的听觉能量. 3 特征 语音分离能够被表达成一个学习问题, 对于机 器学习问题, 特征提取是至关重要的步骤, 提取好的 特征能够极大地提高语音分离的性能. 从特征提取 的基本单位来看, 主要分为时频单元级别的特征和 帧级别的特征. 时频单元级别的特征是从一个时频 单元的信号中提取特征, 这种级别的特征粒度更细, 能够关注到更加微小的细节, 但是缺乏对语音的全 局性和整体性的描述, 无法获取到语音的时空结构 和时序相关性, 另外, 一个时频单元的信号, 很难表 征可感知的语音特性 (例如, 音素). 时频单元级别的 特征主要用于早期以时频单元为建模单元的语音分 离系统中, 例如, 文献 [1, 26, 30−32], 这些系统孤立 地看待每个时频单元, 在每一个频带上训练二值分 类器, 判断每一个频带上的时频单元被语音主导还 是被噪音主导; 帧级别的特征是从一帧信号中提取 的, 这种级别的特征粒度更大, 能够抓住语音的时空 结构, 特别是语音的频带相关性, 具有更好的全局性 和整体性, 具有明显的语音感知特性. 帧级别的特征 主要用于以帧为建模单元的语音分离系统中, 这些 系统一般输入几帧上下文帧级别特征, 直接预测整 帧的分离目标, 例如, 文献 [17−20, 27, 35]. 近年来, 随着语音分离研究的深入, 已有许多听觉特征被提 出并应用到语音分离中, 取得了很好的分离性能. 下 面, 我们简要地总结几种常用的听觉特征. 1) 梅尔倒谱系数 (Mel-frequency cepstral co- efficient, MFCC). 为了计算 MFCC, 输入信号进行 20 ms 帧长和 10 ms 帧移的分帧操作, 然后使用一个 汉明窗进行加窗处理, 利用 STFT 计算能量谱, 再 将能量谱转化到梅尔域, 最后, 经过对数操作和离散 余弦变换 (Discrete cosine transform, DCT) 并联 合一阶和二阶差分特征得到 39 维的 MFCC. 2) PLP (Perceptual linear prediction). PLP 能够尽可能消除说话人的差异而保留重要的共振峰 结构, 一般认为是与语音内容相关的特征, 被广泛应 用到语音识别中. 和语音识别一样, 我们使用 12 阶 的线性预测模型, 得到 13 维的 PLP 特征. 3) RASTA-PLP (Relative spectral trans- form PLP). RASTA-PLP 引入了 RASTA 滤波到 PLP[55], 相对于 PLP 特征, RASTA-PLP 对噪音更 加鲁棒, 常用于鲁棒性语音识别. 和 PLP 一样, 我们 计算 13 维的 RASTA-PLP 特征. 4) GFCC (Gammatone frequency cepstral co- efficient). GFCC 特征是通过 Gammatone 听觉滤 波得到的. 我们对每一个 Gammatone 滤波输出按 照 100 Hz 的采样频率进行采样. 得到的采样通过 立方根操作进行幅度压制. 最后, 通过 DCT 得到 GFCC. 根据文献 [56] 的建议, 一般提取 31 维的 GFCC 特征. 5) GF (Gammatone feature). GF 特征的提取 方法和 GFCC 类似, 只是不需要 DCT 步骤. 一般 提取 64 维的 GF 特征. 6) AMS (Amplitude modulation spectro- gram). 为了计算 AMS 特征, 输入信号进行半波 整流, 然后进行四分之一抽样, 抽样后的信号按照 32 ms 帧长和 10 ms 帧移进行分帧, 通过汉明窗加 窗处理, 利用 STFT 得到信号的二维表示, 并计算 STFT 幅度谱, 最后利用 15 个中心频率均匀分布在 15.6∼ 400 Hz 的三角窗, 得到 15 维的 AMS 特征. 7) 基于基音的特征 (Pitch-based feature). 基 于基音的特征是时频单元级别的特征, 需要对每一 个时频单元计算基音特征. 这些特征包含时频单 元被目标语音主导的可能性. 我们计算输入信号的 Cochleagram, 然后对每一个时频单元计算 6 维的 基音特征, 详细的计算方法可以参考文献 [26, 57]. 8) MRCG (Multi-resolution cochleagram).
    6 期 刘文举等: 基于深度学习语音分离技术的研究现状与进展 823 MRCG 的提取是基于语音信号的 Cochleagram 表 示的. 通过 Gammatone 滤波和加窗分帧处理, 我们 能得到语音信号的 Cochleagram 表示, 然后通过以 下步骤可以计算 MRCG. 步骤 1. 给定输入信号, 计算 64 通道的 Cochle- agram, CG1, 对每一个时频单元取对数操作. 步骤 2. 同样地, 用 200 ms 的帧长和 10 ms 的 帧移计算 CG2. 带的方形窗对 CG1 进行平滑, 得到 CG3. 步骤 3. 使用一个长为 11 时间帧和宽为 11 频 步骤 4. 和 CG3 的计算类似, 使用 23 × 23 的 方形窗对 CG1 进行平滑, 得到 CG4. 个 64 × 4 的向量, 即为 MRCG. 步骤 5. 串联 CG1, CG2, CG3 和 CG4 得到一 MRCG 是一种多分辨率的特征, 既有关注细节 的高分辨率特征, 又有把握全局性的低分辨率特征. 9) 傅里叶幅度谱 (FFT-magnitude). 输入的时 域信号进行分帧处理, 然后对每帧信号进行 STFT, 得到 STFT 系数, 然后对 STFT 进行取模操作即得 到 STFT 幅度谱. 10) 傅里叶对数幅度谱 (FFT-log-magnitude). STFT 对数幅度谱是在 STFT 幅度谱的基础上取对 数操作得到的, 主要目的是凸显信号中的高频成分. 以上介绍的听觉特征是语音分离的主要特征, 这些特征之间既存在互补性又存在冗余性. 研究显 示, 对于单个独立特征, GFCC 和 RASTA-PLP 分 别是噪音匹配条件和噪音不匹配条件下的最好特 征[26]. 基音反映了语音的固有属性, 基于基音的特 征对语音分离具有重要作用, 很多研究显示基于基 音的特征和其他特征进行组合都会显著地提高语音 分离的性能, 而且基于基音的特征非常鲁棒, 对于不 匹配的听觉条件具有很好的泛化性能. 然而, 在噪 音条件下, 准确地估计语音的基音是非常困难, 又 因为缺乏谐波结构, 基于基音的特征仅能用于浊音 段的语音分离, 而无法处理清音段, 因此在实际应用 中, 基于基音的特征很少应用到语音分离中[26], 实际 上, 语音分离和基音提取是一个 “鸡生蛋, 蛋生鸡” 的问题, 它们之间相互促进而又相互依赖. 针对这 一问题, Zhang 等巧妙地将基音提取和语音分离融 合到深度堆叠网络 (Deep stacking network, DSN) 中, 同时提高了语音分离和基音提取的性能[34]. 相 对于基音特征, AMS 同时具有清音和浊音的特性, 能够同时用于浊音段和清音段的语音分离, 然而, AMS 的泛化性能较差[58]. 针对各个特征之间的不 同特性, Wang 等利用 Group Lasso 的特征选择方 法得到 AMS + RASTA − PLP + MFCC 的最优 特征组合[26], 这个组合特征在各种测试条件下取 得了稳定的语音分离性能而且显著地优于单独的 特征, 成为早期语音分离系统最常用的特征. 在低 信噪比条件下, 特征提取对于语音分离至关重要, 相对于其他特征或者组合特征, Chen 等提取的多 分辨率特征 MRCG 表现了明显的优势[27], 逐渐取 代 AMS + RASTA − PLP + MFCC 的组合特征 成为语音分离最常用的特征之一. 在傅里叶变换 域条件下, FFT-magnitude 或 FFT-log-magnitude 是最常用的语音分离特征, 由于高频能量较小, 相 对于 FFT-magnitude, FFT-log-magnitude 能够凸 显高频成分, 但是, 一些研究表明, 在语音分离中, FFT-magnitude 要略好于 FFT-log-magnitude[28]. 语 音 分 离 发 展 到 现 阶 段, MRCG 和 FFT- magnitude 分别成为 Gammtone 域和傅里叶变换 域下最主流的语音分离特征. 此外, 为了抓住信号中 的短时变化特征, 一般还会计算特征的一阶差分和 二阶差分, 同时, 为了抓住更多的信息, 通常输入特 征会扩展上下文帧. Chen 等还提出使用 ARMA 模 型 (Auto-regressive and moving average model) 对 特征进行平滑处理, 来进一步提高语音分离性能[27]. 4 目标 语音分离有许多重要的应用, 总结起来主要有 两个方面: 1) 以人耳作为目标受体, 提高人耳对带 噪语音的可懂度和感知质量, 比如应用于语音通讯; 2) 以机器作为目标受体, 提高机器对带噪语音的识 别准确率, 例如应用于语音识别. 对于这两个主要的 语音分离目标, 它们存在许多密切的联系, 例如, 以 提高带噪语音的可懂度和感知质量为目标的语音分 离系统通常可以作为语音识别的前端处理模块, 能 够显著地提高语音识别的性能[59], Weninger 等指 出语音分离系统的信号失真比 (Signal-to-distortion ratio, SDR) 和语音识别的字错误率 (Word error rate, WER) 有明显的相关性[5], Weng 等将多说话 人分离应用于语音识别中也显著地提高了识别性 能[6]. 尽管如此, 它们之间仍然存在许多差别, 以提 高语音的可懂度和感知质量为目标的语音分离系统 侧重于去除混合语音中的噪音成分, 往往会导致比 较严重的语音畸变, 而以提高语音识别准确率为目 标的语音分离系统更多地关注语音成分, 在语音分 离过程中尽可能保留语音成分, 避免语音畸变. 针对 语音分离两个主要目标, 许多具体的学习目标被提 出, 常用的分离目标大致可以分为三类: 时频掩蔽、 语音幅度谱估计和隐式时频掩蔽. 其中时频掩蔽和 语音幅度谱估计的目标被证明能显著地抑制噪音, 提高语音的可懂度和感知质量[17−18]. 而隐式时频掩 蔽通常将掩蔽技术融入到实际应用模型中, 时频掩 蔽作为中间处理过程来提高其他目标的性能, 例如 语音识别[5, 60]、目标语音波形的估计[21].
    824 4.1 时频掩蔽 自 动 化 学 报 42 卷 时频掩蔽是语音分离的常用目标, 常见的时频 掩蔽有理想二值掩蔽和理想浮值掩蔽, 它们能显著 地提高分离语音的可懂度和感知质量. 一旦估计出 了时频掩蔽目标, 如果不考虑相位信息, 通过逆变 换技术即可合成目标语音的时域波形. 但是, 最近 的一些研究显示, 相位信息对于提高语音的感知质 量具有重要的作用[50]. 为此, 一些考虑相位信息的 时频掩蔽目标被相继提出, 例如复数域的浮值掩蔽 (Complex ideal ratio mask, CIRM)[53]. 1) 理想二值掩蔽 (Ideal binary mask, IBM). 理想二值掩蔽 (IBM) 是计算听觉场景分析的主要计 算目标[61], 已经被证明能够极大地提高分离语音的 可懂度[44−47, 62]. IBM 是一个二值的时频掩蔽矩阵, 通过纯净的语音和噪音计算得到. 对于每一个时频 单元, 如果局部信噪比 SN R(t, f) 大于某一局部阈 值 (Local criterion, LC), 掩蔽矩阵中对应的元素标 记为 1, 否则标记为 0. 具体来讲, IBM 的定义如下: IBM(t, f) = 1, 若 SN R(t, f) > LC 0, 其他 (7) 其中, SN R(t, f) 定义了时间帧为 t 和频率为 f 的 时频单元的局部信噪比. LC 的选择对语音的可懂 度具有重大的影响[63], 一般设置 LC 小于混合语音 信噪比 5 dB, 这样做的目的是为了保留足够多的语 音信息. 例如, 混合语音信噪比是 −5 dB, 则对应的 LC 设置为 −10 dB. 2) 目标二值掩蔽 (Target binary mask, TBM). 类似于 IBM, 目标二值掩蔽 (TBM) 也是一个二值 的时频掩蔽矩阵. 不同的是, TBM 是通过纯净语 音的能量和一个固定的参照噪音 (Speech-shaped noise, SSN) 的能量计算得到的. 也就是说, 在式 (7) 中的 SN R(t, f) 项是用参考的 SSN 而不是实际的 噪音计算的. 尽管 TBM 的计算独立于噪音, 但是实 验测试显示 TBM 取得了和 IBM 相似的可懂度提 高[63]. TBM 能够提高语音的可懂度的原因是它保 留了与语音感知密切相关的时空结构模式, 即语音 能量在时频域上的分布. 相对于 IBM, TBM 可能更 加容易学习. 3) Gammtone 域的理想浮值掩蔽 (Gammtone ideal ratio mask, IRM Gamm) 理想浮值掩蔽定义如下: β = (8) β S2(t, f) S2(t, f) + N 2(t, f) SN R(t, f) SN R(t, f) + 1 IRMgamm(t, f) = 其中, S2(t, f) 和 N 2(t, f) 分别定义了混合语音中 时间帧为 t 和频率为 f 的时频单元的语音和噪音的 能量. β 是一个可调节的尺度因子. 如果假定语音 和噪音是不相关的, 那么 IRM 在形式上和维纳滤波 密切相关[9, 64]. 大量的实验表明 β = 0.5 是最好的 选择, 此时, 式 (8) 和均方维纳滤波器非常相似, 而 维纳滤波是最优的能量谱评估[9]. 4) 傅里叶变换域的理想浮值掩蔽 (FFT ideal ratio mask, IRM FFT). 类似于 Gammtone 域的 理想浮值掩蔽, 傅里叶域的理想浮值掩蔽 IRM FFT 的定义如下: IRMF F T (t, f) = |Ys(t, f)|2 |Ys(t, f)|2 + |Yn(t, f)|2 = Ps(t, f) Ps(t, f) + Pn(t, f) (9) 其中, Ys(t, f) 和 Yn(t, f) 是混合语音中纯净的语音 和噪音的短时傅里叶变换系数. Ps(t, f) 和 Pn(t, f) 分别是它们对应的能量密度. 5) 短时傅里叶变换掩蔽 (Short-time Fourier transform mask, FFT-Mask). 不同于 IRM FFT, FFT-Mask 的定义如下: M askF F T (t, f) = |Ys(t, f)| |X(t, f)| (10) 其中, Ys(t, f) 和 X(t, f) 是纯净的语音和混合语音 的短时傅里叶变换系数. IRM FFT 的取值范围在 [0, 1], 显然 FFT-Mask 的取值范围可以超过 1. 6) 最 优 浮 值 掩 蔽 (Optimal ratio time- frequency mask, ORM). 理想浮值掩蔽 (IRM) 是 假定在语音和噪音不相关的条件下, 能够取得最小 均方误差意义下最大信噪比增益[42−43]. 然而在真实 环境中, 语音和噪音通常存在一定的相关性, 针对这 个问题, Liang 等[42−43] 推导出一般意义下的最小均 方误差的最优浮值掩蔽, 定义如下: ORM(t, f) = Ps(t, f) + (Ys(t, f)Y ∗ n (t, f)) Ps(t, f) + Pn(t, f) + 2(Ys(t, f)Y ∗ n (t, f)) (11) 其中, (·) 表示取复数的实部, ∗ 表示共轭操作. 相 对于 IRM, ORM 考虑了语音和噪音的相关性, 其变 化范围更大, 估计难度也更大. 7) 复数域的理想浮值掩蔽 (Complex ideal ra- tio mask, CIRM). 传统的 IRM 定义在幅度域, 而 CIRM 定义在复数域. 其目标是通过将 CIRM 作用 到带噪语音的 STFT 系数得到目标语音的 STFT
    6 期 刘文举等: 基于深度学习语音分离技术的研究现状与进展 825 系数. 具体地, 给定带噪语音在时间帧为 t 和频率为 f 的时频单元的 STFT 系数 X, 那么目标语音在对 应时频单元的 STFT 系数 Y 可以通过下式计算得 到: Y = M × X (12) 其中, × 定义复数乘法操作, M 定义时间帧为 t 和 频率为 f 的时频单元的 CIRM. 通过数学推导我们 能计算得到: M = XrYr + XiYi r + X 2 X 2 i + j XrYi − XiYr r + X 2 X 2 i (13) 其中, Xr 和 Yr 分别是 X 和 Y 的实部, Xi 和 Yi 分 别是 X 和 Y 的虚部, j 是虚数单位. 定义 Mr 和 Mi 分别是 M 的实部和虚部, 那么, X 2 Mr = XrYr + XiYi r + X 2 Mi = XrYi − XiYr r + X 2 X 2 i i (14) (15) 在实际语音分离中通常不会直接估计复数域的 M, 而是通过估计其实部 Mr 和虚部 Mi. 但 Mr 和 Mi 的取值可能会超过 [0, 1], 这往往会增大 Mr 和 Mi 估计难度. 因此, 在实际应用中通常会利用双曲 正切函数对 Mr 和 Mi 进行幅度压制. 4.2 语音幅度谱估计 如果不考虑相位的影响, 语音分离问题可以转 化为目标语音幅度谱的评估, 一旦从混合语音中评 估出了目标语音的幅度谱, 利用混合语音的相位信 息, 通过逆变换即可得到目标语音的波形. 常见的幅 度谱包括 Gammtone 域幅度谱和 STFT 幅度谱. 1) Gammtone 域 幅 度 谱 (Gammatone fre- quency power spectrum, GF-POW). 时域信号经 过 Gammtone 滤波器组滤波和分帧加窗处理, 可 以得到二维的时频表示 Cochleagram. 直接估计 目标语音的 Gammtone 域幅度谱 (GF-POW) 能 够实现语音的分离. 对于 Gammtone 滤波, 由于 没有直接的逆变换方法, 我们可以通过估计的 GF- POW 和混合语音的 GF-POW 构造一个时频掩蔽 GF (t, f) 来合成目标语音的波形, 其 中, S2 GF (t, f) 分别是纯净语音和混合 语音在 Gammtone 域下时间帧为 t 和频带为 f 的 时频单元的能量. GF (t, f)/X 2 S2 GF (t, f) 和 X 2 2) 短时傅里叶变换幅度谱 (Short-time Fourier transform spectral magnitude, FFT-magnitude). 时域信号经过分帧加窗处理, 然后通过 STFT, 可以 得到二维的时频表示, 如果不考虑相位的影响, 我们 可以直接估计目标语音的 STFT 幅度谱, 利用原始 混合语音的相位, 通过 IFTST 可以估计得到目标语 音的时域波形. 4.3 隐式时频掩蔽 语音分离旨在从混合语音中分离出语音成分, 尽管可以通过估计理想时频掩蔽来分离目标语音, 但理想时频掩蔽是一个中间目标, 并没有针对实际 的语音分离应用直接优化最终的实际目标. 针对这 些问题, 隐式时频掩蔽被提取, 在这些方法中, 时频 掩蔽作为一个确定性的计算过程被融入到具体应用 模型中, 例如识别模型或者分离模型, 它们并没有估 计理想时频掩蔽, 其最终的目标是估计目标语音的 幅度谱甚至是波形, 或者提高语音识别的准确率. Huang 等提出将掩蔽融合到目标语音的幅度谱 估计中[19, 28]. 在文献 [29] 中, 深度神经网络作为语 音分离模型, 时频掩蔽函数作为额外的处理层加入 到网络的原始输出层, 如图 2 所示, 通过时频掩蔽, 目标语音的幅度谱从混合语音的幅度谱中估计出来. 其中时频掩蔽函数 Ms 和 Mn 通过神经网络原始输 出 (语音和噪音幅度谱的初步估计) 计算得到的, 如 下: Ms = |ˆyyys| |ˆyyys| + |ˆyyyn| , Mn = |ˆyyyn| |ˆyyys| + |ˆyyyn| (16) 图 2 Huang 等提出的声源分离系统的网络结构[28] Fig. 2 The network structure of the proposed source separation system by Huang et al.[28] 一旦时频掩蔽被计算出来, 就可以通过掩蔽技 术从混合语音的幅度谱 X 估计出语音和噪音的幅 度谱 ˜yyys 和 ˜yyyn: ˜yyys = Ms ⊗ X, ˜yyyn = Mn ⊗ X (17)
    826 自 动 化 学 报 42 卷 需要注意的是原始的网络输出并不用来计算误 差函数, 仅仅用来计算时频掩蔽函数, 时频掩蔽函数 是确定性的, 并没有连接权重, 掩蔽输出用来计算误 差并以此来更新模型参数. Wang 等提出将时频掩蔽融合到目标语音波形 估计中[21], 在文献 [21] 中, 时频掩蔽作为神经网络 的一部分, 掩蔽函数从混合语音的 STFT 幅度谱估 计目标语音的 STFT 幅度谱, 然后通过 ISTFT, 利 用混合语音的相位信息和估计的 STFT 幅度谱合成 目标语音的时域波形, 如图 3 所示, 估计的时域波形 与目标波形计算误差, 最后通过反向传播更新网络 权重. 假设 mmm 是最后一个隐层的输出, 它可以看成 是估计的掩蔽, 用来从混合语音的 STFT 幅度谱 xxx 中估计目标语音的 STFT 幅度谱 ˜yyys. ˜yyys = mmm ⊗ xxx (18) 评估的目标语音幅度谱加上对应的混合语音的相位 ppp 输入到逆傅里叶变换层能够得到目标语音的时域 波形信号. ˆsss = IFFT([ccc, flipud((ccc2:d)∗)]T) (19) 其中, ccc 是目标语音的傅里叶变换系数, 它能够通过 下面的公式得到: ccc = ˜yyys ⊗ ejppp (20) d = F/2, F 是傅里叶变换的分析窗长. flipud 定义 了向量的上下翻转操作, ∗ 是复数的共轭操作. 下标 m : n 取向量从 m 到 n 的元素的操作. 图 3 Wang 等提出的语音分离系统的网络结构[21] Fig. 3 The network structure of the proposed speech separation system by Wang et al. 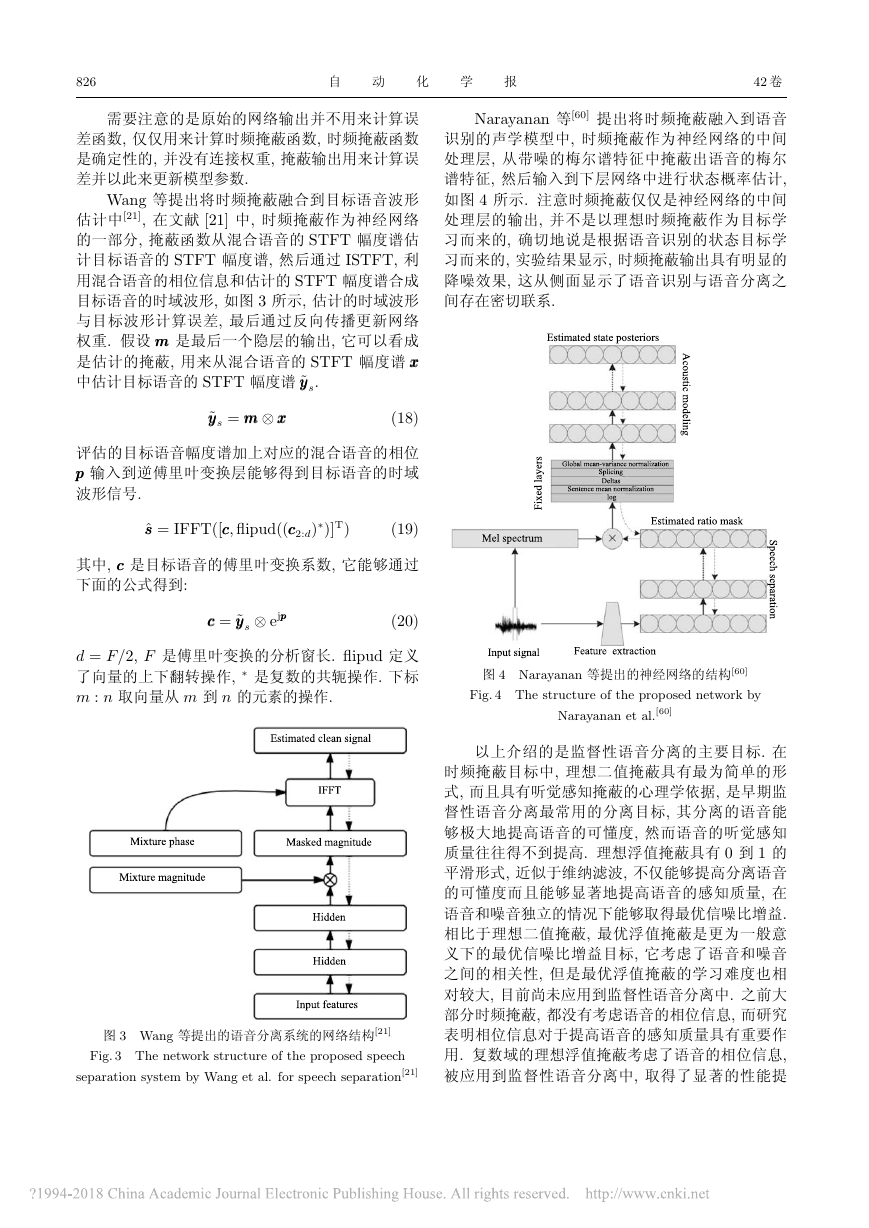for speech separation[21] Narayanan 等[60] 提出将时频掩蔽融入到语音 识别的声学模型中, 时频掩蔽作为神经网络的中间 处理层, 从带噪的梅尔谱特征中掩蔽出语音的梅尔 谱特征, 然后输入到下层网络中进行状态概率估计, 如图 4 所示. 注意时频掩蔽仅仅是神经网络的中间 处理层的输出, 并不是以理想时频掩蔽作为目标学 习而来的, 确切地说是根据语音识别的状态目标学 习而来的, 实验结果显示, 时频掩蔽输出具有明显的 降噪效果, 这从侧面显示了语音识别与语音分离之 间存在密切联系. 图 4 Narayanan 等提出的神经网络的结构[60] Fig. 4 The structure of the proposed network by Narayanan et al.[60] 以上介绍的是监督性语音分离的主要目标. 在 时频掩蔽目标中, 理想二值掩蔽具有最为简单的形 式, 而且具有听觉感知掩蔽的心理学依据, 是早期监 督性语音分离最常用的分离目标, 其分离的语音能 够极大地提高语音的可懂度, 然而语音的听觉感知 质量往往得不到提高. 理想浮值掩蔽具有 0 到 1 的 平滑形式, 近似于维纳滤波, 不仅能够提高分离语音 的可懂度而且能够显著地提高语音的感知质量, 在 语音和噪音独立的情况下能够取得最优信噪比增益. 相比于理想二值掩蔽, 最优浮值掩蔽是更为一般意 义下的最优信噪比增益目标, 它考虑了语音和噪音 之间的相关性, 但是最优浮值掩蔽的学习难度也相 对较大, 目前尚未应用到监督性语音分离中. 之前大 部分时频掩蔽, 都没有考虑语音的相位信息, 而研究 表明相位信息对于提高语音的感知质量具有重要作 用. 复数域的理想浮值掩蔽考虑了语音的相位信息, 被应用到监督性语音分离中, 取得了显著的性能提
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料