第1页 / 共17页
第2页 / 共17页
第3页 / 共17页
第4页 / 共17页
第5页 / 共17页
第6页 / 共17页
第7页 / 共17页
第8页 / 共17页
乘法器的verilog HDL设计汇总.docx
乘法器的verilog HDL设计汇总
乘法器的 verilog HDL 设计汇总
1、移位相加乘法器的设计：
其大致原理如下：
Verilog HDL 代码如下：
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
//移位相加乘法器的 verilog HDL 代码
module multi_Mov_Add(a,b,outcome);
parameter size = 8;
input [size - 1 : 0] a, b; //a,b 为乘法器的两个输入
output [2*size - 1 : 0] outcome;
reg [2*size - 1 : 0] outcome;
integer i;
always @ (a or b)
begin
outcome = 4'b0;
for(i = 0; i < size; i = i + 1) //用于移位
begin
if(b[i] == 1) //如果被乘数为 1，则移位相加
begin
outcome = outcome + (a<
end
19.
20. endmodule
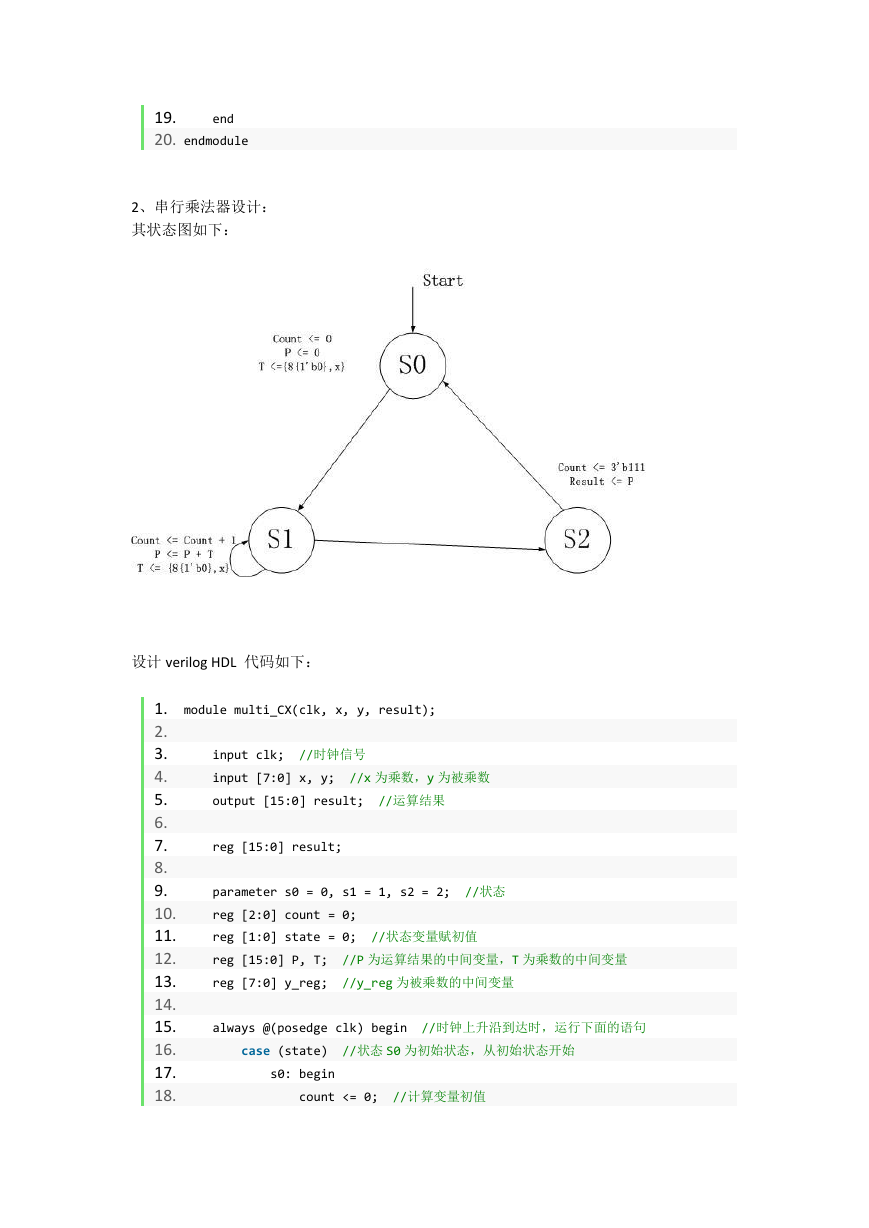
2、串行乘法器设计：
其状态图如下：
设计 verilog HDL 代码如下：
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
module multi_CX(clk, x, y, result);
//时钟信号
input clk;
input [7:0] x, y;
output [15:0] result;
//x 为乘数，y 为被乘数
//运算结果
reg [15:0] result;
//状态
parameter s0 = 0, s1 = 1, s2 = 2;
reg [2:0] count = 0;
reg [1:0] state = 0;
reg [15:0] P, T;
reg [7:0] y_reg;
//状态变量赋初值
//P 为运算结果的中间变量，T 为乘数的中间变量
//y_reg 为被乘数的中间变量
always @(posedge clk) begin
//时钟上升沿到达时，运行下面的语句
case (state)
s0: begin
//状态 S0 为初始状态，从初始状态开始
count <= 0; //计算变量初值
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
//结果变量清零
P <= 0;
y_reg <= y; //被乘数赋初值
T <= {{8{1'b0}}, x};
state <= s1;
//进入下一个状态
//乘数赋初值
end
s1: begin
//S1 状态
if(count == 3'b111) //计数为 3'b111，即 7 时，进入结束状态
state <= s2;
else begin
//未进入结束状态
if(y_reg[0] == 1'b1)
//被乘数末尾位为 1 时
P <= P + T;
//中间结果加一次乘数
else
//否则中间结果不变
P <= P;
y_reg <= y_reg >> 1;
T <= T << 1;
//被乘数右移一位，倒数第二位移到末尾
//乘加一次后，被乘数左移一位，这里从运算过程中
可以看出
个时钟周期
count <= count + 1;
//count 是为了统计运行一次乘法需要多少
state <= s1;
end
end
s2: begin
result <= P;
state <= s0;
//结束状态时，中间结果赋值给最终结果
//为下一次运算准备
end
default: ;
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46. endmodule
end
endcase
缺点：计算一次乘法需要 8 个周期，因此可以看出串行乘法器速度比较慢，时延大。
优点：该乘法器所占用的资源是所有类型乘法器中最少的，在低速的信号处理中有广泛的使
用。
3、流水线乘法器
其 verilog HDL 设计如下：
1.
2.
3.
4.
5.
module multi_4bits_pipelining(mul_a, mul_b, clk, rst_n, mul_out);
input [3:0] mul_a, mul_b; //乘数与被乘数
input clk; //时钟信号
input rst_n; //复位信号
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
output [7:0] mul_out; //结果变量
reg [7:0] mul_out;
reg [7:0] stored0; //stored0,...stored3 用来存逐位相乘的中间结果
reg [7:0] stored1;
reg [7:0] stored2;
reg [7:0] stored3;
reg [7:0] add01; //中间结果变量
reg [7:0] add23;
always @(posedge clk or negedge rst_n) begin
if(!rst_n) begin //复位信号有效
mul_out <= 0;
stored0 <= 0;
stored1 <= 0;
stored2 <= 0;
stored3 <= 0;
add01 <= 0;
add23 <= 0;
end
else begin
stored0 <= mul_b[0] ? {4'b0, mul_a} : 8'b0; //如果被乘数倒数第一位
不为零，则与乘数相乘结果为{4'b0,mul_a}
stored1 <= mul_b[1] ? {3'b0, mul_a, 1'b0} : 8'b0; //如果被乘数倒
数第二位不为零，则与乘数相乘结果为{3'b0,mul_a,1'b0}
stored2 <= mul_b[2] ? {2'b0, mul_a, 2'b0} : 8'b0; //同上
stored3 <= mul_b[3] ? {1'b0, mul_a, 3'b0} : 8'b0; //同上
add01 <= stored1 + stored0;
add23 <= stored3 + stored2;
mul_out <= add01 + add23; //最终结果
27.
28.
29.
30.
31.
32.
33.
34. endmodule
end
end
Verilog HDL 代码我都加上了注释，增加了可读性，我认为这是代码起码的尊严，也是对阅读
者起码的尊重。原理就不多赘述，很简单，读懂代码即可了解。
4、
Wallace 树乘法器
在乘法器的设计中采用树形乘法器，可以减少关键路径和所需的加法器单元数目，
Wallace 树乘法器就是其中的一种。下面以一个 4*4 位乘法器为例介绍 Wallace 树乘法器及
其 Verilog HDL 实现。
从数据最密集的地方开始，不断的反复使用全加器、半加器来覆盖“树”。全加器是一
个 3 输入 2 输出的器件，因此全加器又称作 3—2 压缩器。通过全加器将树的深度不断缩减，
最终缩减为一个深度为 2 的树。最后一级则采用简单的 2 输入加法器组成。
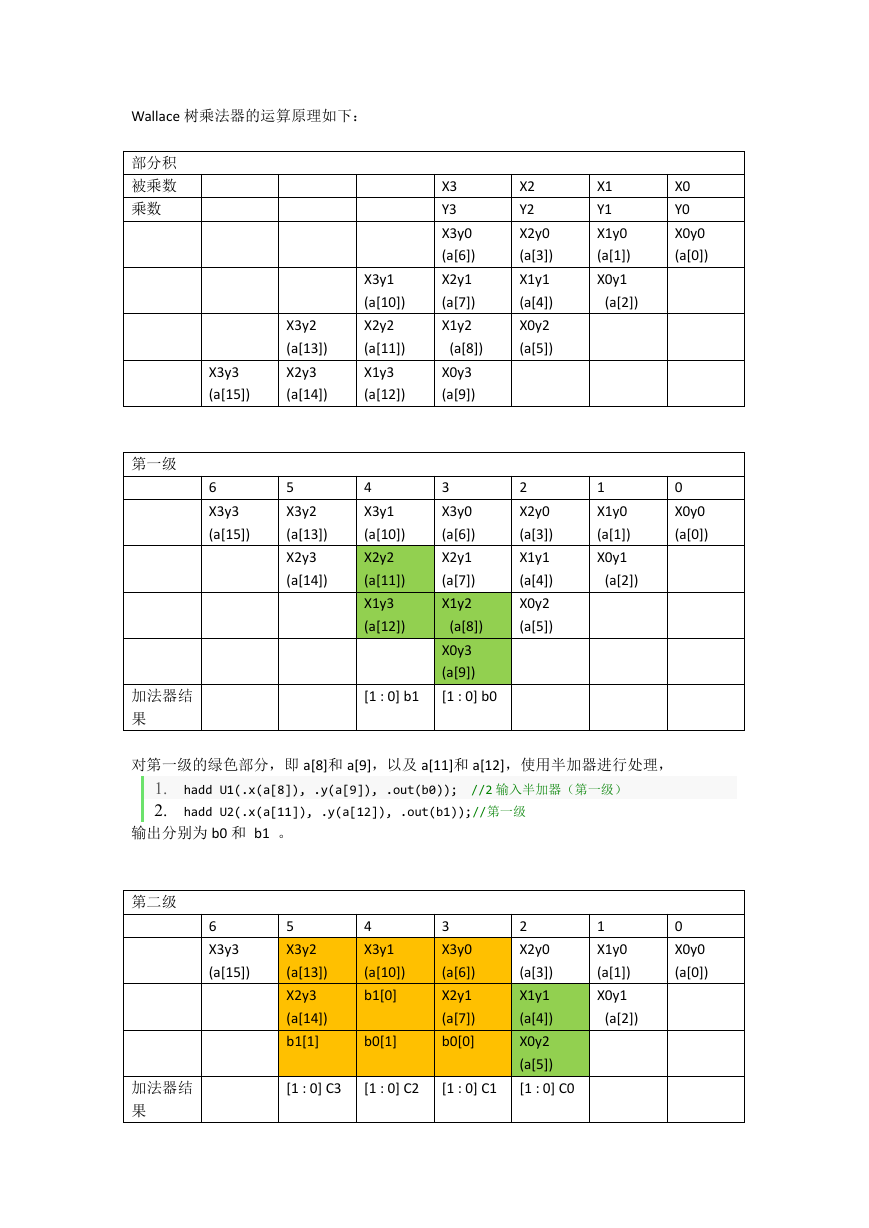
Wallace 树乘法器的运算原理如下：
部分积
被乘数
乘数
第一级
加法器结
果
X3y3
(a[15])
6
X3y3
(a[15])
X3y2
(a[13])
X2y3
(a[14])
5
X3y2
(a[13])
X2y3
(a[14])
X0
Y0
X0y0
(a[0])
X1
Y1
X1y0
(a[1])
X0y1
(a[2])
0
X0y0
(a[0])
1
X1y0
(a[1])
X0y1
(a[2])
X2
Y2
X2y0
(a[3])
X1y1
(a[4])
X0y2
(a[5])
2
X2y0
(a[3])
X1y1
(a[4])
X0y2
(a[5])
X3
Y3
X3y0
(a[6])
X2y1
(a[7])
X1y2
(a[8])
X0y3
(a[9])
3
X3y0
(a[6])
X2y1
(a[7])
X1y2
(a[8])
X0y3
(a[9])
[1 : 0] b0
X3y1
(a[10])
X2y2
(a[11])
X1y3
(a[12])
4
X3y1
(a[10])
X2y2
(a[11])
X1y3
(a[12])
[1 : 0] b1
对第一级的绿色部分，即 a[8]和 a[9]，以及 a[11]和 a[12]，使用半加器进行处理，
1.
2.
hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2 输入半加器（第一级）
hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级
输出分别为 b0 和 b1 。
第二级
6
X3y3
(a[15])
5
X3y2
(a[13])
X2y3
(a[14])
b1[1]
4
X3y1
(a[10])
b1[0]
b0[1]
3
X3y0
(a[6])
X2y1
(a[7])
b0[0]
加法器结
果
[1 : 0] C3
[1 : 0] C2
[1 : 0] C1
0
X0y0
(a[0])
1
X1y0
(a[1])
X0y1
(a[2])
2
X2y0
(a[3])
X1y1
(a[4])
X0y2
(a[5])
[1 : 0] C0
半加器仍然用绿色部分表示，全加器用橙色部分表示，第二级经过半加器以及全加器的处理，
即：
1.
2.
3.
4.
第三级
6
X3y3
(a[15])
C3[1]
hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级
fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3 输入全加器（第二级）
fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2));
fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3));
5
C3[0]
C2[1]
4
C2[0]
C1[1]
3
C1[0]
C0[1]
2
X2y0
(a[3])
C0[0]
0
X0y0
(a[0])
1
X1y0
(a[1])
X0y1
(a[2])
其在 verilog HDL 代码中的体现如下：
1.
2.
3.
4.
assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器（第三极）
assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]};
assign add_out = add_a + add_b;
assign out = {add_out,a[0]};
其 verilog HDL 代码如下：
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
module wallace(x,y,out);
parameter size = 4; //定义参数，乘法器的位数
input [size - 1 : 0] x,y; //输入 y 是乘数，x 是被乘数
output [2*size - 1 : 0] out;
wire [size*size - 1 : 0] a; //a 为部分积
wire [1 : 0] b0, b1; //第一级的输出，包含进位
wire [1 : 0] c0, c1, c2, c3; //第二级的输出，包含进位
wire [5 : 0] add_a, add_b; //第三极的输入
wire [6 : 0] add_out; //第三极的输出
wire [2*size - 1 : 0] out; //乘法器的输出（组合逻辑）
assign a = {x[3],x[2],x[3],x[1],x[2],x[3],x[0],x[1],
x[2],x[3],x[0],x[1],x[2],x[0],x[1],x[0]}
&{y[3],y[3],y[2],y[3],y[2],y[1],y[3],y[2]
,y[1],y[0],y[2],y[1],y[0],y[1],y[0],y[0]}; //部分积
hadd U1(.x(a[8]), .y(a[9]), .out(b0));
hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级
hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级
//2 输入半加器（第一级）
fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3 输入全加器（第二级）
fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2));
fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3));
assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器（第三极）
assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]};
assign add_out = add_a + add_b;
assign out = {add_out,a[0]};
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31. endmodule
32.
33. //全加器模块
34. module fadd(x, y, z, out);
35.
36.
37.
38. endmodule
39.
40. //半加器模块
41. module hadd(x, y, out);
42.
43.
44.
45. endmodule
input x, y;
output [1 : 0] out;
assign out = x + y;
input x, y, z;
output [1 : 0] out;
assign out = x + y + z;
这里继续贴合其测试文件：
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
//测试文件
`timescale 1ns/1ps
module wallace_tb;
reg [3 : 0] x, y;
wire [7 : 0] out;
wallace U1(.x(x), .y(y), .out(out)); //模块实例
initial
begin
x = 3;
y = 4;
# 20
x = 2;
y = 3;
# 20
x = 6;
y = 8;
12.
13.
14.
15.
16.
17.
18.
19.
20.
21. endmodule
end
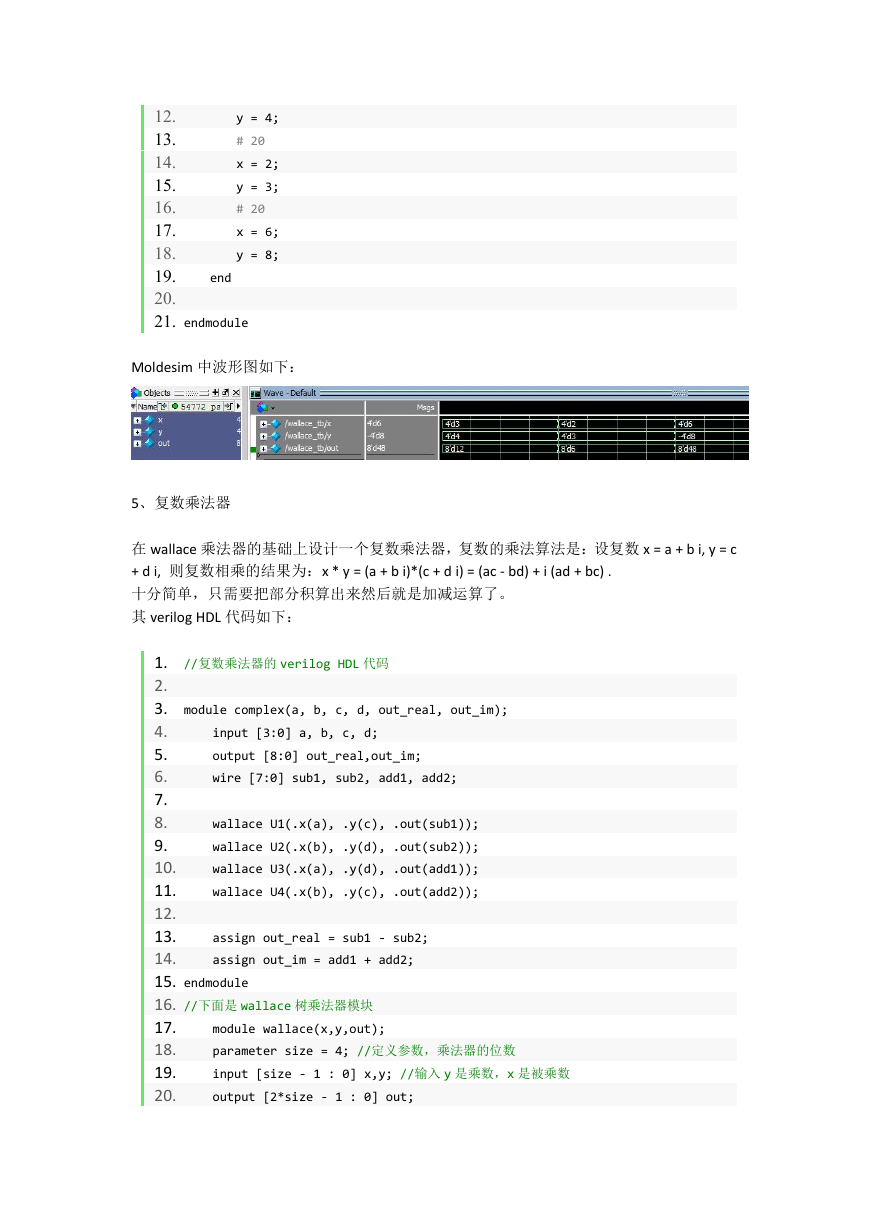
Moldesim 中波形图如下：
5、复数乘法器
在 wallace 乘法器的基础上设计一个复数乘法器，复数的乘法算法是：设复数 x = a + b i, y = c
+ d i, 则复数相乘的结果为：x * y = (a + b i)*(c + d i) = (ac - bd) + i (ad + bc) .
十分简单，只需要把部分积算出来然后就是加减运算了。
其 verilog HDL 代码如下：
module complex(a, b, c, d, out_real, out_im);
input [3:0] a, b, c, d;
output [8:0] out_real,out_im;
wire [7:0] sub1, sub2, add1, add2;
wallace U1(.x(a), .y(c), .out(sub1));
wallace U2(.x(b), .y(d), .out(sub2));
wallace U3(.x(a), .y(d), .out(add1));
wallace U4(.x(b), .y(c), .out(add2));
//复数乘法器的 verilog HDL 代码
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15. endmodule
16. //下面是 wallace 树乘法器模块
17.
18.
19.
20.
assign out_real = sub1 - sub2;
assign out_im = add1 + add2;
module wallace(x,y,out);
parameter size = 4; //定义参数，乘法器的位数
input [size - 1 : 0] x,y; //输入 y 是乘数，x 是被乘数
output [2*size - 1 : 0] out;
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
