第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
论文研究-基于线性相位的宽带微波信号相位谱频域对准方法 .pdf
中国科技论文在线
http://www.paper.edu.cn
基于线性相位的宽带微波信号相位谱频域
对准方法#
林茂六，时远海*
（哈尔滨工业大学电子与信息工程学院，哈尔滨 150001）
摘要：随着测量仪器的快速发展，我们在获得宽带微波信号精确幅度谱的同时也能够获得其
精确的相位谱。在实际测量中，同一个波形用不同时窗测得的相位谱是不同的，这就使得比
较不同时窗测得的相位谱比较困难。频域对准算法可以将不同时窗测得的多频正弦信号相位
谱对准，以便多次测量可以比较。本文提出基于线性相位的频域对准算法，解决了以往频域
对准算法不易处理相位从 到 跳变的问题。通过仿真和实测处理结果证实了该方法的正确
性、通用性和有效性。
关键词：多频正弦信号；相位分析；线性相位；非线性失真；频域对准
中图分类号：TN98
Frequency domain alignment method based on linear phase
for phase spectrum of wide-bandwidth microwave signals
Lin Maoliu, Shi Yuanhai
(School of Electronic and Infirmation Enginiring,Harbin Institute of Technology,Harbin 150001)
Abstract: Advances in measuring instrument now, it is feasible to accurately measure both the
magnitude spectrum and the phase spectrum of wide-bandwidth microwave signals. In a practical
measurement, the spectrum magnitude is independent of the position of the time-domain window,
allowing straightforward comparison of measurements made at different time, the spectrum phase is
dependent on the position of the time-domain window, resulting the phase spectrums to differ between
repeated measurements of an identical waveform. So it is difficult to measure the spectrum phase and
to compare multiple phase spectrum measurements with different starting time of the time-domain
window, or to incorporate several measurements into a model. Frequency domain alignment for
measured multisine signals is a straightforward method for determining the phase spectrum such that
multiple measurements can be effectively compared. We present a novel method called frequency
domain alignment based on linear phase, which solve the problem that frequency domain alignment is
difficult to deal with phase variation from -180 degree to +180 degree. Processing results of simulation
and measurement verify the correctness, generality and efficiency of this method.
Keywords:multisine;phase analysis;linear phase;nonlinear distortion;frequency domain alignment
0 引言
为了测试、表征和改正超宽带（DC-毫米波）通信、雷达等电子系统的性能，非线性系
统的宽带幅度和相位的精准测量变得极其重要。微波、毫米波电路及器件的大信号表征更是
近年来一个十分活跃的研究领域[1-3]。然而为了完整地探索由新颖的测量仪器测得的矢量信
息，宽带相位问题必须全面仔细研究。众所周知，在实际测量中，频谱是在有限的时窗内测
得的。对于一个周期信号而言，幅度谱 与时窗位置无关，相位谱与时窗位置相关。即对同
基金项目：国家自然科学基金（NO.：60772078）；教育部博士点基金（NO.：20070213026）；武器装备
预研基金。
作者简介：林茂六，男，(1943-)。现任哈尔滨工业大学教授，通信与信息工程学科博士点博士生导师。目
前主要的研究方向包括现代数字信号处理、统计学习理论与应用以及无线系统非线性表征、辨识与评估、
视频可伸缩性编解码、动态频谱接入网络、认知无线电等. E-mail: mllin20060810@yahoo.com.cn
- 1 -
中国科技论文在线
http://www.paper.edu.cn
一个波形测量，时间窗的起始时刻不同测得的幅度谱是相同的，相位谱却存在很大的差异。
这就是所谓的“测得的相位是时变的”含义[4]。多频正弦信号具有广泛的用途，由于它能够
逼近复杂的数字调制信号，因此在实际的微波毫米波测试中，常用作已调激励信号来测量射
频功放等非线性器件的非线形特性[5]。相位随时间是线性变化的，频域对准算法[6]可以消除
两个不同时刻测量的多频正弦信号之间的相位线性变化成分，以便不同时窗下测量的多个多
频正弦信号相位谱能够进行比较或合并建立模型。以往提出的频域对准算法处理相位从
180o
− 到180o 跳变时往往会遇到困难，本文提出基于线性相位的频域对准算法，较好地解决
了这个难题，并且通过仿真和实验验证了该算法的正确性、通用性和有效性。
1 频域对准算法
多频正弦信号是由一些同时产生的正弦波集合，式(1)给出了其典型的数学模型：
x t
( )
=
N
∑
i
1
=
A
i
cos(
tω θ
)
i
+
i
(1)
其中，Ai 表示第 i 个正弦波分量的幅度， iθ表示第 i 个正弦波分量的初相位，N 表示正
弦波分量的总数。式中：
i
i
(
=
1)
+ − Δ (2)
ω ω
0
其中， 0ω 表示第一个正弦波分量的角频率， ωΔ 表示相邻频率分量之间的固定角频率间
ω
隔。
设一个三音多频正弦信号，其幅度相等，初相位分别为 1
0oθ = ，载频
为 800MHz，频率间隔为 200MHz，通过仿真可以看到每个正弦波分量随时间变化的情况，
如图 1 所示。该三音多频正弦信号的载波周期为 1.25ns
，包络周期为 5ns
0oθ = ， 3
0oθ = ， 2
T = 。
pt =
Fig.1 Changing status with time of three-tone multsine signal
图 1 三音多频正弦信号各频率分量随时间变化情况
117o
θ = − ， 2
当用矢量信号源产生该信号时，记产生时刻为 reft ，理想情况下，此时相位值为 1
0οθ = ，
0oθ = 。信号源产生重复的周期信号，用一台测量仪器在另一时刻 Mt 对该信号测
0oθ = ， 3
2
θ = 。其值与 reft 时刻相位值无明显关系。如
量，得到相位值为 1
果我们能够通过 Mt 时刻的测量值推算出 reft ，就能将 Mt 时刻测量的相位值向前移动 M
t− 时
t
间，从而可以将不同时刻测量的两组相位值进行比较。频域对准算法的核心就是由 Mt 时刻
测量数据估计出最理想的 reft 时刻值。频域对准算法中提到两个概念：目标相位和目标时刻。
目标相位是已知的作为参考的一组相位值，可以选择仪器设置的初相位为目标相位，也可以
θ = − ， 3
36o
45o
ref
- 2 -
中国科技论文在线
http://www.paper.edu.cn
用测量仪器第一次测量的相位值作为目标相位，或者由测量仪器测得的多组相位值处理后得
出目标相位。目标时刻是信号的每个频率分量均达到目标相位时所对应的时刻，通常用 reft 表
示。
根据相位随时间线性变化的关系，由测量时刻相位值可以得到任意时刻的相位值，两者
关系如下：
t
(
=
θ θ
i M
i
其中，t 表示任意时刻， Mt 表示测量时刻， if 表示多频正弦信号第i 个频率分量的频率，
(3)
) 2
+
f
π
t
( )
t
(
−
)
t
M
i
i tθ 表示t 时刻第 i 个频率分量的相位值， (
( )
i Mtθ 表示 Mt 时刻第i 个频率分量的相位值。
)
既然由式(3)可以获得任意时刻上的相位，那么我们就可以将任意时刻上的相位分别与
目标相位进行比较，选择等于或者与目标相位值最接近的一组相位值作为对准的相位值，其
所在的时刻即可认为是最理想的目标时刻估计值，称为 final
t 。
t 是 reft 的最佳估计值，我们需要定义一个误差函数：
为了保证找到的 final
2
E t
( )
=
tθ θ
i tar
i
,
( )
−
N
∑
i
1
=
(4)
其中，N 表示多频正弦信号频率分量的总数。 ,i tarθ 表示每个频率分量对应的目标相位值，
使得误差函数 ( )E t 取最小值的时刻记为 final
t 。
− 。式(3)求的相位值往往不在 180o
相位随时间线性变化的同时也是以 360o 为模重复出现的，通常我们认为相位的180o 即
为 180o
− 至
180o 之间，由于数据量大，变换过程的工作量很大。如果目标相位 ,i tarθ 在180o 附近，那么 final
时刻的实测相位值既可能在 0o 到180o 之间，也有可能在 0o 到 180o
− 至180o 之间，所以需要将其求模变换到 180o
t
tθ θ−
i tar
i
,
− 至180o 之间然后求和，否则计算结果是错误的。以往的
求得的数值需要再一次变换到 180o
频域对准算法中并没有阐述何时需要变换，如果不进行第二次求模变换，某些情况下计算结
t 时刻的相
果是错误的。例如，三音多频正弦信号的目标相位分别为180o 、180o 、180o ， final
− 。不进行第二次变换直接利用式(4)得到的误差函数值为 128886，
位为178o 、179o 、 179o
显然是不正确的，包含变换过程得到的误差函数值是 6，是正确的。
2 基于线性相位的频域对准算法
− 之间。式(4)中
( )
显然，上述算法中需要用到两次求模变换，算法复杂且运算量大，为此我们提出基于线
性相位的频域对准算法[7]，在不影响对准精度的情况下使得整个算法过程只需要一次求模变
换，明显减少运算量。
)
−
)
)
θ
i tar
,
(5)
i Mtθ 表示 Mt 时刻测得的瞬时相位，那么测量时刻的线性相位成分即为：
我们以 (
t
t
(
(
φ
=
θ
i M
i M
任意时刻的线性相位与 Mt 时刻的线性相位之间的关系可表示为：
t
(
φ φ
i M
i
由于 reft 时刻所有频率分量的线性相位值相等且均为 0o ，可得：
(
φ
l
(6)
) 2
+
t
(
φ
l M
) 2
+
f
π
t
( )
f
π
φ
h
=
−
t
(
−
=
(
t
(
t
=
−
)
t
M
t
M
)
t
M
)
t
ref
ref
ref
t
ref
)
)
i
l
即
(
t
ref
−
t
)
M est
=
h
=
t
(
φ
h M
t
(
)
φ
h M
f
2 (
π
f
) 2
π
+
t
(
φ
−
l M
f
)
−
h
l
(
)
(7)
- 3 -
中国科技论文在线
http://www.paper.edu.cn
其中，下标 l 和下标 h 表示相邻两个频率分量，通常 l 与 h 取各频率分量中靠近中间的
h Mtφ 一般不会等于理想
t ，
两个分量。由于信号产生与测量的误差以及失真的影响， (
为估计值，用下标 est 表示，此时对应的 reft 时刻估计值记为 refest
值，因此时间差 (
t 的估计误差应小于包络周期T 。为了找到 reft 的最佳估值，定义一个平方求和函数：
l Mtφ 与 (
)
M est
t−
refest
ref
)
)
t
N
取 refest
S t
( )
2
tφ
( )
i
(8)
= ∑
t 时刻附近一个时间段内的相位值，将其带入找到全局最小值。全局最小值所对应
1
=
i
的时刻可以认为是 reft 的最好表示，记为 final
t 。然后由式(3)得到其对应的相位值 (
tθ
i
final
)
。
由于相位以 360o 为模，所以在计算误差函数时存在许多局部最小值，但一个包络周期
内只有一个全局最小值。通常，得到的全局最小值不为边界上的局部最小值时则接受，若为
边界局部最小值则需扩大搜索范围寻找全局最小值。我们用矢量信号源产生幅度相等，初相
位分别为 45o 、 0o 、 0o ，载频为 800MHz，频率间隔为 10MHz 的三音多频正弦信号，用非
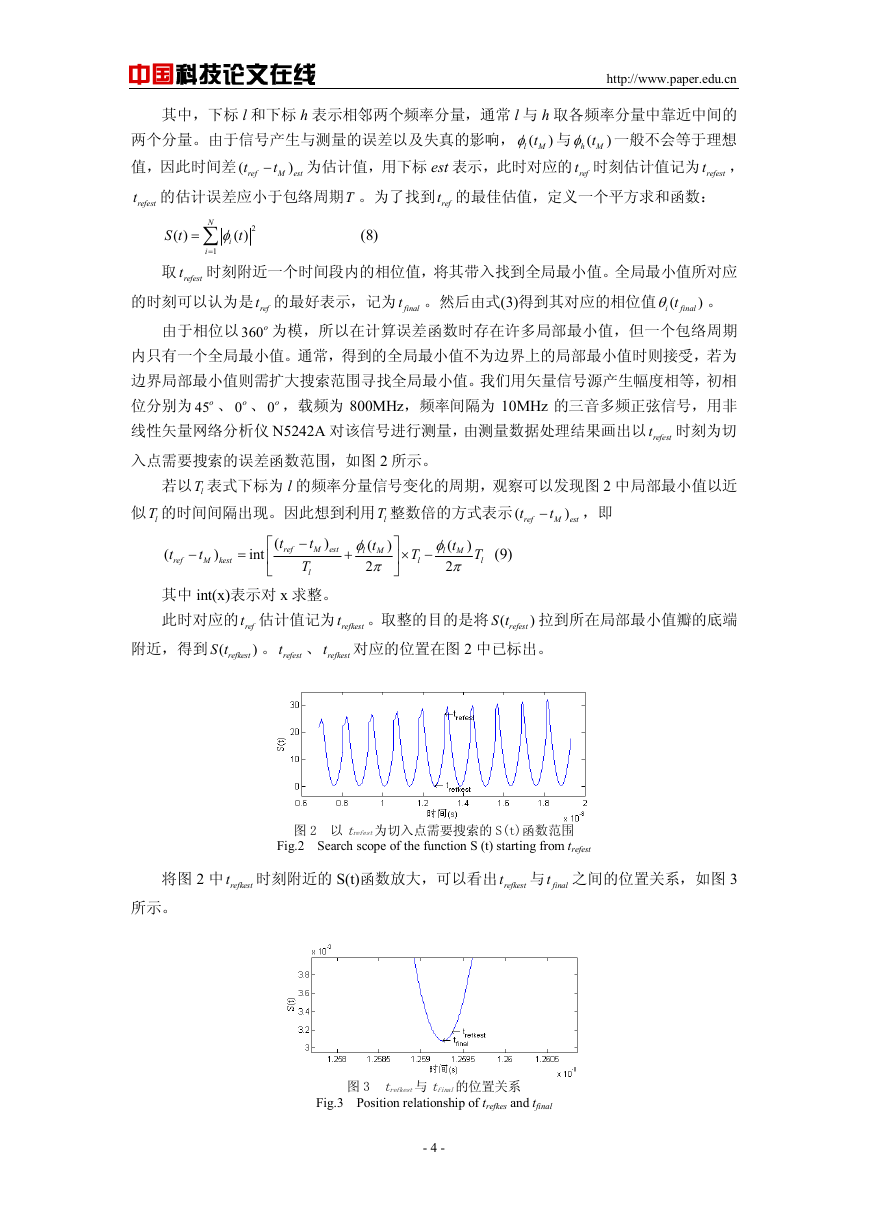
线性矢量网络分析仪 N5242A 对该信号进行测量，由测量数据处理结果画出以 refest
t 时刻为切
入点需要搜索的误差函数范围，如图 2 所示。
若以 lT 表式下标为 l 的频率分量信号变化的周期，观察可以发现图 2 中局部最小值以近
似 lT 的时间间隔出现。因此想到利用 lT 整数倍的方式表示 (
t
ref
t−
)
M est
，即
(
t
ref
−
t
)
M kest
=
int
)
M est
(
t
ref
⎡
⎢
⎣
t
−
T
l
+
)
t
(
φ
l M
2
π
⎤
⎥
⎦
T
× −
l
)
t
(
φ
l M
2
π
T
l
(9)
其中 int(x)表示对 x 求整。
此时对应的 reft 估计值记为 refkest
t 。取整的目的是将 (
S t 拉到所在局部最小值瓣的底端
)
refest
S t
附近，得到 (
)
refkest
。 refest
t 、 refkest
t 对应的位置在图 2 中已标出。
图 2 以 trefest为切入点需要搜索的 S(t)函数范围
Fig.2 Search scope of the function S (t) starting from trefest
将图 2 中 refkest
t 时刻附近的 S(t)函数放大，可以看出 refkest
t 与 final
t 之间的位置关系，如图 3
所示。
图 3 trefkest与 tfinal的位置关系
Fig.3 Position relationship of trefkes and tfinal
- 4 -
中国科技论文在线
http://www.paper.edu.cn
以 refkest
t 为切入点比用 refest
t 为切入点能够更快的搜索到局部最小值，从而可以更快的获得
全局最小值。通常我们搜索不超过 10 个局部最小值即可获得全局最小值。然而，如果不先
寻找切入点，直接用式(8)计算一个包络周期的 ( )S t 函数，同样可以找到全局最小值，但是需
要搜索约 80 个局部最小值。需要注意的是，通常情况下 refest
t 在同一个局部最小值瓣
上，但并不一定和 final
t 与 refkest
t 在同一个局部最小值瓣上。因此，当找到 refkest
t 后，我们需要寻找多个
⋅⋅⋅ ，一般 n 小于 5，搜索这些切入点所在瓣的局部最小值，
± × ，其中 0,1,2
n =
t
切入点 refkest
从而找到全局最小值。
n T
l
得到 refkest
t
± × 之后，可以采用 Nelder-Mead 搜索算法[8-9]搜索局部最小值，既可以提
n T
l
高搜索速度，又可以减少系统资源占用率。
我们设计理想情况下的仿真用于验证基于线性相位的频域对准算法的正确性。仿真条件
如下：幅度相等，初相位分别为 45o 、 0o 、 0o ，载频为 800MHz，频率间隔为 10MHz 的三
音多频正弦信号。随机选择测量时刻 0.598ns，此时相位值为87.12o 、 57.60o
、157.68o 。由
该算法计算得：(
= ，
= −
最终对准相位值分别为 45o 、 0o 、 0o ， ( )S t 函数值为 0。
0.598ns
)
M est
，即
0ns
M final
M kest
refkest
refest
final
(
t
−
t
−
t
−
t
=
t
=
t
=
t
(
t
ref
=
ref
ref
−
t
)
)
为了验证基于线性相位的频域对准算法的通用性，我们进行了四种不同类型的多频正弦
信号实验分析。这些信号均由矢量信号源 E4438C 产生：幅度相等，载频为 800MHz，频率
间隔为 10MHz；前两个多频正弦信号为三音，后两个为七音。用非线性矢量网络分析仪
N5242A 测量，处理结果见表 1。
表 1 不同类型多频正弦信号处理结果
Table 1 Different multsine signals processing results
信号源设置
相位（ o ）
0、0、0
45、0、0
0、0、0、0、
0、0、0
0、-51、-154、
51、-154、-51、
0
测得的相位值
对准后相位值
（ o ）
（ o ）
12.230、-36.239、
-82.977
2.464、-0.560 、
-1.851
66.077、-26.989、
-74.048
130.162、
-142.806、
47.415、-0.316、
-2.043
8.521、-4.208、
-2.681、-0.960、
2.682、4.456、
-7.494
-0.305、-61.955、
-160.549、51.547、
-149.584、
-41.739、2.825
-41.518、59.965、
163.368、-95.095、
-7.284
136.177、-68.634、
49.609、118.542、
134.249、98.931、
0.333
S（t）函
数值
9.810
10.407
181.636
276.543
通过对四种不同类型的多频正弦信号分析，说明基于线性相位的频域对准算法适用于以
下情况：不同音数、不同相位、相位对称或非对称、不同峰均比的多频正弦信号。表 1 中对
准后相位值与信号源设置的相位值存在误差，这是由于信号产生与测量的误差以及失真引起
的。减小对准后相位值误差的一个途径是减小多频正弦信号的频率间隔。
3 射频功率放大器性能表征
频域对准算法不仅可以用于一端口对准，同样可以用于多端口网络。以双端口放大器为
例，频域对准算法可以求出信号通过放大器的线性相位延时（包括传播延时和线性相位失真）
- 5 -
中国科技论文在线
http://www.paper.edu.cn
以及放大器对输入信号产生的高阶相位失真。实际测量中当被测设备是反相放大器时，放大
器输出电压和输入电压的相位相差180o ，若输入的多频正弦信号中某个频率分量的初相位是
0o ，并以 0o 作为放大器输入端的目标相位，则放大器输出端的目标相位应为180o 。以往的
频域对准算法对于这种情况处理过程复杂，而基于线性相位的频域对准算法则可以减少一次
求模变换，简化了算法的复杂度。
Fig.4 Amplifier measurement structure and signal relationship of amplifier input port and output port
图 4 功放测量结构图及功放两端信号关系
放大器输入端，以信号源设定的初相位为目标相位， Min
即输入端的 final
以反相功率放大器为例，图 4 给出了测量功放的结构示意图及功放两端的信号关系。在
t 表示测量时刻，可得目标时刻 refin
t ，
t
π+ 为目标相位， Mout
t ，以及实测初相位 (
tθ
i
表示测量时刻，可得目标时刻 refout
refout
时刻之间的关系，我们可以得到放大器对输入信号产生的线性相位延时 tΔ ：
tθ
；在放大器输出端，以 (
i
t ，以及实测初相位 (
tθ
i
t ，即输出端的 final
。通过各个
refin
refin
)
)
)
t
t
t
)
(
−
−
−
Min
t
(
Mout
refout
t
Δ =
同时，以放大器输出端与输入端的相位差可以反应放大器的高阶相位失真：
(
θ θ
Δ =
i
(11)
(10)
(
π θ
− −
i
refout
refin
refin
)
t
)
)
t
i
tθ
同相放大器的测量结构与反相放大器一样，对准时放大器输出端的目标相位取 (
i
refin
)
，
高阶相位失真应为
(
θ θ
Δ =
i
i
t
refout
)
−
(
θ
i
t
refin
)
，其余过程相同。
设置矢量信号源 E4438C 产生七音多频正弦信号，信号幅度相等，初相位均为 0o ，载频
为 800MHz，频率间隔为 10MHz。反相放大器增益为 28dB，带宽为 0.5GHz-1.1GHz。测量
仪器选用非线性矢量网络分析仪 N5242A，测量频率间隔为 10MHz，频率范围从 600MHz
到 2GHz。按图 4 所示结构搭建仪器，调节信号源输出功率，使放大器分别工作于线性区，
1dB 压缩点位置，非线性区三种状态。
我们得到三种情况下的线性相位延时。
=
线性：
1dB 压缩：
(2.72990 10 )
8
−
(6.02648 10 )
8
−
0.4657(ns)
(5.97807 10 )
8
−
(2.77647 10 )
8
−
×
−
×
×
×
−
(4.97443 10 )
8
×
−
=
=
0.5401(ns)
0.4841(ns)
非线性：
(5.02844 10 )
8
−
×
−
三种情况下线性相位延时呈现逐渐增大的趋势，由于传播延时是不变的，说明线性相位
失真随着放大器输入端功率的增大而增大。
- 6 -
中国科技论文在线
http://www.paper.edu.cn
按照非线性矢量网络分析仪测试的习惯，下文中 A1 表示信号源输出电压信号，B1 表
示放大器输入端反射电压信号，Vin 表示放大器输入端电压信号，Vout 表示放大器输出端电
压信号。
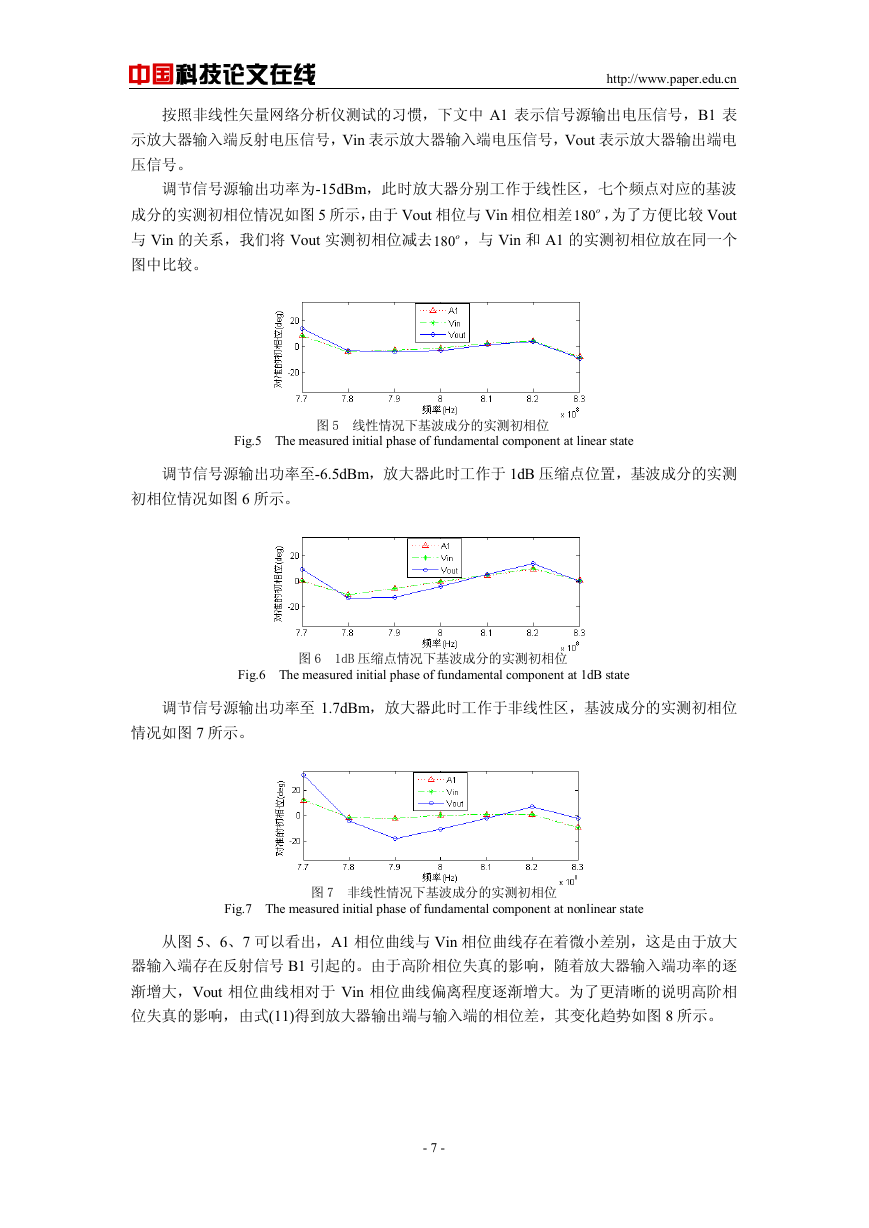
调节信号源输出功率为-15dBm，此时放大器分别工作于线性区，七个频点对应的基波
成分的实测初相位情况如图 5 所示，由于 Vout 相位与 Vin 相位相差180o ，为了方便比较 Vout
与 Vin 的关系，我们将 Vout 实测初相位减去180o ，与 Vin 和 A1 的实测初相位放在同一个
图中比较。
图 5 线性情况下基波成分的实测初相位
Fig.5 The measured initial phase of fundamental component at linear state
调节信号源输出功率至-6.5dBm，放大器此时工作于 1dB 压缩点位置，基波成分的实测
初相位情况如图 6 所示。
图 6 1dB 压缩点情况下基波成分的实测初相位
Fig.6 The measured initial phase of fundamental component at 1dB state
调节信号源输出功率至 1.7dBm，放大器此时工作于非线性区，基波成分的实测初相位
情况如图 7 所示。
图 7 非线性情况下基波成分的实测初相位
Fig.7 The measured initial phase of fundamental component at nonlinear state
从图 5、6、7 可以看出，A1 相位曲线与 Vin 相位曲线存在着微小差别，这是由于放大
器输入端存在反射信号 B1 引起的。由于高阶相位失真的影响，随着放大器输入端功率的逐
渐增大，Vout 相位曲线相对于 Vin 相位曲线偏离程度逐渐增大。为了更清晰的说明高阶相
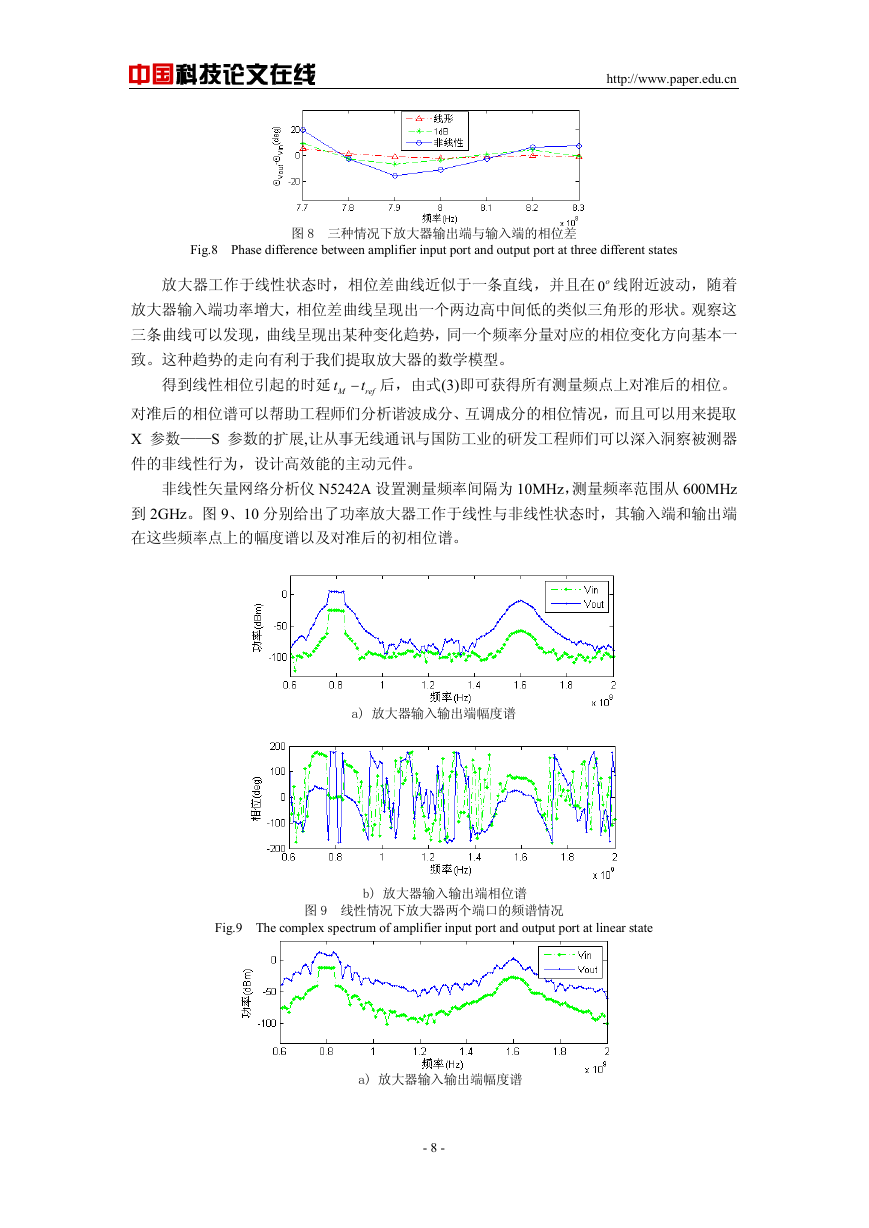
位失真的影响，由式(11)得到放大器输出端与输入端的相位差，其变化趋势如图 8 所示。
- 7 -
中国科技论文在线
http://www.paper.edu.cn
Fig.8 Phase difference between amplifier input port and output port at three different states
图 8 三种情况下放大器输出端与输入端的相位差
放大器工作于线性状态时，相位差曲线近似于一条直线，并且在 0o 线附近波动，随着
放大器输入端功率增大，相位差曲线呈现出一个两边高中间低的类似三角形的形状。观察这
三条曲线可以发现，曲线呈现出某种变化趋势，同一个频率分量对应的相位变化方向基本一
致。这种趋势的走向有利于我们提取放大器的数学模型。
t
得到线性相位引起的时延 M
t− 后，由式(3)即可获得所有测量频点上对准后的相位。
ref
对准后的相位谱可以帮助工程师们分析谐波成分、互调成分的相位情况，而且可以用来提取
X 参数——S 参数的扩展,让从事无线通讯与国防工业的研发工程师们可以深入洞察被测器
件的非线性行为，设计高效能的主动元件。
非线性矢量网络分析仪 N5242A 设置测量频率间隔为 10MHz，测量频率范围从 600MHz
到 2GHz。图 9、10 分别给出了功率放大器工作于线性与非线性状态时，其输入端和输出端
在这些频率点上的幅度谱以及对准后的初相位谱。
a) 放大器输入输出端幅度谱
b) 放大器输入输出端相位谱
图 9 线性情况下放大器两个端口的频谱情况
Fig.9 The complex spectrum of amplifier input port and output port at linear state
a) 放大器输入输出端幅度谱
- 8 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
