三次简化一张图: 一招理解 LSTM/GRU 门控机制 张皓 zhangh0214@gmail.com 引言 RNN 是深度学习中用于处理时序数据的关键技术, 目前已在自然语言处理, 语音识别, 视 频识别等领域取得重要突破, 然而梯度消失现象制约着 RNN 的实际应用. LSTM 和 GRU 是 两种目前广为使用的 RNN 变体, 它们通过门控机制很大程度上缓解了 RNN 的梯度消失问 题, 但是它们的内部结构看上去十分复杂, 使得初学者很难理解其中的原理所在. 本文介 绍”三次简化一张图”的方法, 对 LSTM 和 GRU 的内部结构进行分析. 该方法非常通用, 适 用于所有门控机制的原理分析. 预备知识: RNN RNN (recurrent neural networks, 注意不是recursive neural networks)提供了一种 处理时序数据的方案. 和 n-gram 只能根据前 n-1 个词来预测当前词不同, RNN 理论上可 以根据之前所有的词预测当前词. 在每个时刻, 隐层的输出 ht 依赖于当前词输入 xt 和前一 时刻的隐层状态 ht-1: 其中:=表示"定义为", sigm 代表 sigmoid 函数 sigm(z):=1/(1+exp(-z)), Wxh 和 Whh 是 可学习的参数. 结构见下图: 图中左边是输入, 右边是输出. xt 是当前词, ht-1 记录了上文的信息. xt 和 ht-1 在分别乘以 Wxh 和 Whh 之后相加, 再经过 tanh 非线性变换, 最终得到 ht. 在反向传播时, 我们需要将 RNN 沿时间维度展开, 隐层梯度在沿时间维度反向传播时需要 反复乘以参数 . 因此, 尽管理论上 RNN 可以捕获长距离依赖, 但实际应用中, 根据 谱 半径(spectral radius)的不同, RNN 将会面临两个挑战: 梯度爆炸(gradient explosion) 和梯度消失(vanishing gradient). 梯度爆炸会影响训练的收敛, 甚至导致网络不收敛; 而 梯度消失会使网络学习长距离依赖的难度增加. 这两者相比, 梯度爆炸相对比较好处理, 可 以用梯度裁剪(gradient clipping)来解决, 而如何缓解梯度消失是 RNN 及几乎其他所有深 度学习方法研究的关键所在. 

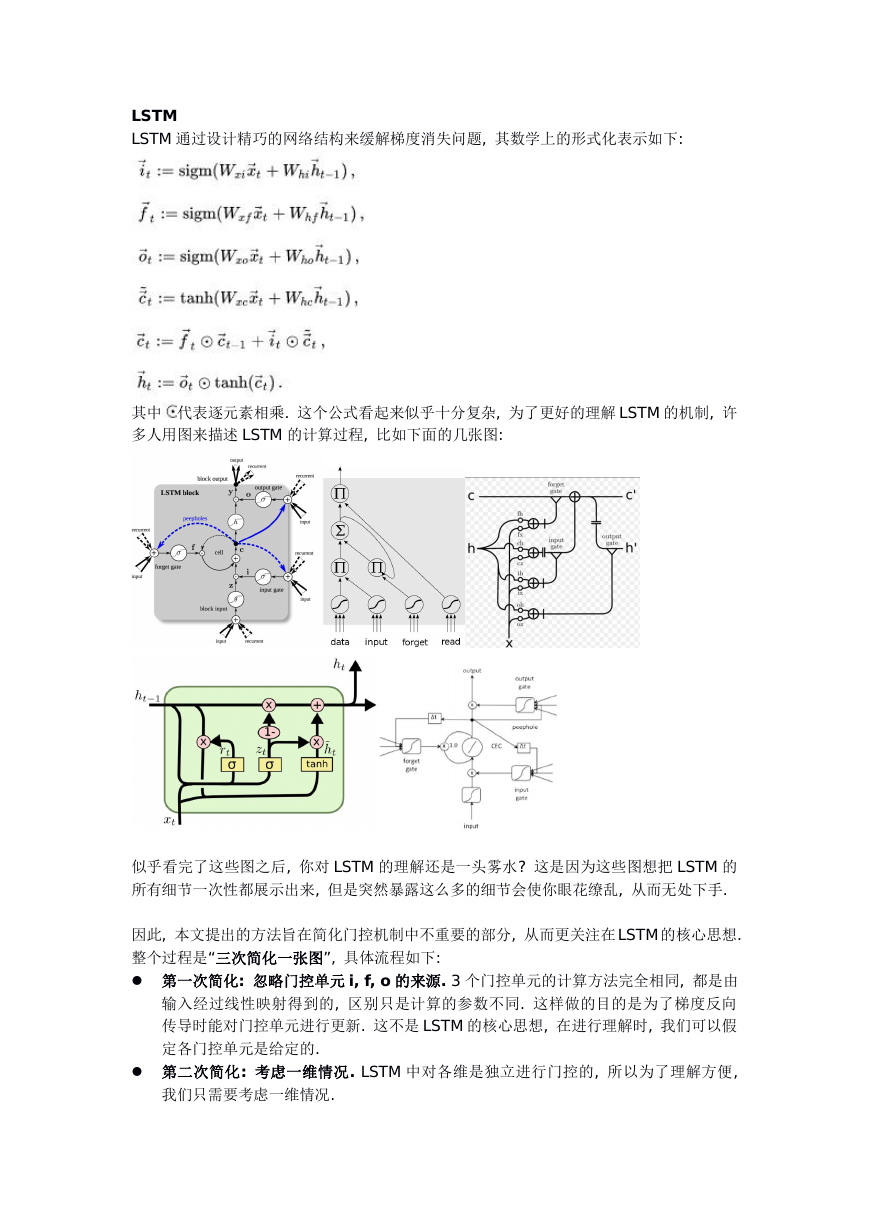
LSTM LSTM 通过设计精巧的网络结构来缓解梯度消失问题, 其数学上的形式化表示如下: 其中 代表逐元素相乘. 这个公式看起来似乎十分复杂, 为了更好的理解 LSTM 的机制, 许 多人用图来描述 LSTM 的计算过程, 比如下面的几张图: 似乎看完了这些图之后, 你对 LSTM 的理解还是一头雾水? 这是因为这些图想把 LSTM 的 所有细节一次性都展示出来, 但是突然暴露这么多的细节会使你眼花缭乱, 从而无处下手. 因此, 本文提出的方法旨在简化门控机制中不重要的部分, 从而更关注在LSTM 的核心思想. 整个过程是“三次简化一张图”, 具体流程如下:  第一次简化: 忽略门控单元 i, f, o 的来源. 3 个门控单元的计算方法完全相同, 都是由 输入经过线性映射得到的, 区别只是计算的参数不同. 这样做的目的是为了梯度反向 传导时能对门控单元进行更新. 这不是 LSTM 的核心思想, 在进行理解时, 我们可以假 定各门控单元是给定的.  第二次简化: 考虑一维情况. LSTM 中对各维是独立进行门控的, 所以为了理解方便, 我们只需要考虑一维情况. 

 第三次简化: 各门控单元 0/1 输出. 门控单元输出是[0, 1]实数区间的原因是阶跃激活 函数无法反向传播进行优化, 所以各门控单元使用 sigmoid 激活函数去近似阶跃函数. 因此, 为了理解方便, 我们只需要考虑理想情况, 即各门控单元是{0, 1}二值输出的, 即门控单元扮演了电路中”开关”的角色, 用于控制信息传输的通断.  一张图: 将三次简化的结果用”电路图”表述出来, 左边是输入, 右边是输出. 另外需要 特别注意的是 LSTM 中的 c 实质上起到了 RNN 中 h 的作用, 这点在其他文献资料中 不常被提到. 最终结果如下: 和 RNN 相同的是, 网络接受两个输入, 得到一个输出. 不同之处在于, LSTM 中通过 3 个门 控单元来对记忆单元 c 的信息进行交互. 根据这张图, 我们可以对 LSTM 中各单元作用进行分析:  输入门 it: it 控制当前词 xt 的信息融入记忆单元 ct. 在理解一句话时, 当前词 xt 可能对 整句话的意思很重要, 也可能并不重要. 输入门的目的就是判断当前词 xt 对全局的重 要性. 当 it 开关打开的时候, 网络将不考虑当前输入 xt.  遗忘门 ft: ft 控制上一时刻记忆单元 ct-1 的信息融入记忆单元 ct. 在理解一句话时, 当 前词 xt 可能继续延续上文的意思继续描述, 也可能从当前词 xt 开始描述新的内容, 与 上文无关. 和输入门 it 相反, ft 不对当前词 xt 的重要性作判断, 而判断的是上一时刻的 记忆单元 ct-1 对计算当前记忆单元 ct 的重要性. 当 ft 开关打开的时候, 网络将不考虑上 一时刻的记忆单元 ct-1.  输出门 ot: 输出门的目的是从记忆单元 ct 产生隐层单元 ht. 并不是 ct 中的全部信息都 和隐层单元 ht 有关, ct 可能包含了很多对 ht 无用的信息, 因此, ot 的作用就是判断 ct 中哪些部分是对 ht 有用的, 哪些部分是无用的.  记忆单元 ct: ct 综合了当前词 xt 和前一时刻记忆单元 ct-1 的信息. 这和 ResNet 中的 残差逼近思想十分相似, 通过从 ct-1 到 ct 的”短路连接”, 梯度得已有效地反向传播. 当 ft 处于闭合状态时, ct 的梯度可以直接沿着最下面这条短路线传递到 ct-1, 不受参数 W 的影响, 这是 LSTM 能有效地缓解梯度消失现象的关键所在. GRU GRU 是另一种十分主流的 RNN 衍生物. RNN 和 LSTM 都是在设计网络结构用于缓解梯度 消失问题, 只不过是网络结构有所不同. GRU 在数学上的形式化表示如下: 

为了理解 GRU 的设计思想, 我们再一次运用“三次简化一张图”的方法来进行分析:  第一次简化: 忽略门控单元 z, r 的来源.  第二次简化: 考虑一维情况.  第三次简化: 各门控单元 0/1 输出. 这里和 LSTM 略有不同的地方在于, GRU 需要引 入一个”单刀双掷开关”.  一张图: 把三次简化的结果用”电路图”表述出来, 左输入, 右输出: 与 LSTM 相比, GRU 将输入门 it 和遗忘门 ft 融合成单一的更新门 zt, 并且融合了记忆单元 ct 和隐层单元 ht, 所以结构上比 LSTM 更简单一些. 根据这张图, 我们可以对 GRU 的各单元作用进行分析:  重置门 rt: rt 用于控制前一时刻隐层单元ht-1 对当前词 xt 的影响. 如果ht-1 对 xt 不重要, 即从当前词 xt 开始表述了新的意思, 与上文无关, 那么 rt 开关可以打开, 使得 ht-1 对 xt 不产生影响.  更新门 zt: zt 用于决定是否忽略当前词 xt. 类似于 LSTM 中的输入门 it, zt 可以判断当 前词 xt 对整体意思的表达是否重要. 当 zt 开关接通下面的支路时, 我们将忽略当前词 xt, 同时构成了从ht-1 到ht的”短路连接”, 这梯度得已有效地反向传播. 和LSTM 相同, 这种短路机制有效地缓解了梯度消失现象, 这个机制于highway networks 十分相似. 小结 尽管RNN, LSTM, 和GRU 的网络结构差别很大, 但是他们的基本计算单元是一致的, 都是 对xt 和ht-1 做一个线性映射加 tanh 激活函数, 见三个图的红色框部分. 他们的区别在于如 何设计额外的门控机制控制梯度信息传播用以缓解梯度消失现象. LSTM 用了 3 个门, GRU 用了 2 个, 那能不能再少呢? MGU (minimal gate unit)尝试对这个问题做出回答, 它只有 一个门控单元. 最后留个小练习, 参考 LSTM 和 GRU 的例子, 你能不能用“三次简化一张 图”的方法来分析一下 MGU 呢? 

参考文献 1. Bengio, Yoshua, Patrice Simard, and Paolo Frasconi. "Learning long-term dependencies with gradient descent is difficult." IEEE transactions on neural networks 5.2 (1994): 157-166. 2. Cho, Kyunghyun, et al. "Learning phrase representations using RNN for statistical machine translation." arXiv preprint encoder-decoder arXiv:1406.1078 (2014). 3. Chung, Junyoung, et al. "Empirical evaluation of gated recurrent neural networks on sequence modeling." arXiv preprint arXiv:1412.3555 (2014). 4. Gers, Felix. "Long short-term memory in recurrent neural networks." Unpublished PhD dissertation, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland (2001). 5. Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016. 6. Graves, Alex. Supervised sequence labelling with recurrent neural networks. Vol. 385. Heidelberg: Springer, 2012. 7. Greff, Klaus, et al. "LSTM: A search space odyssey." IEEE transactions on neural networks and learning systems (2016). 8. He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. 9. He, Kaiming, et al. "Identity mappings in deep residual networks." European Conference on Computer Vision. Springer International Publishing, 2016. 10. Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780. 11. Jozefowicz, Rafal, Wojciech Zaremba, and Ilya Sutskever. "An empirical exploration of recurrent network architectures." Proceedings of the 32nd International Conference on Machine Learning (ICML-15). 2015. 12. Li, Fei-Fei, Justin Johnson, and Serena Yeung. CS231n: Convolutional Neural Networks for Visual Recognition. Stanford. 2017. 13. Lipton, Zachary C., John Berkowitz, and Charles Elkan. "A critical review of sequence learning." arXiv preprint for recurrent neural networks arXiv:1506.00019 (2015). 14. Manning, Chris and Richard Socher. CS224n: Natural Language Processing with Deep Learning. Stanford. 2017. 15. Pascanu, Razvan, Tomas Mikolov, and Yoshua Bengio. "On the difficulty of training recurrent neural networks." International Conference on Machine Learning. 2013. 16. Srivastava, Rupesh Kumar, Klaus Greff, and Jürgen Schmidhuber. "Highway networks." arXiv preprint arXiv:1505.00387 (2015). 17. Williams, D. R. G. H. R., and Geoffrey Hinton. "Learning representations by back-propagating errors." Nature 323.6088 (1986): 533-538. 18. Zhou, Guo-Bing, et al. "Minimal gated unit for recurrent neural networks." International Journal of Automation and Computing 13.3 (2016): 226-234.