logo资料库

FFT的在电力系统中的应用.docx

发布时间：2022-06-06 发布人：admin 分类：说明书 资料大小：0.06M 资料格式：docx 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    一、课题背景及研究意义 电力系统的谐波问题早在 20 世纪 20 年代和 30 年代就引起了人们的注意。各种 电力电子装置在电力系统、工业、交通及家庭中的应用日益广泛，谐波所造成的 危害也日趋严重。谐波使电能的生产、传输和利用的效率降低，使电气设备过热、 产生振动和噪声，并使绝缘老化，使用寿命缩短，甚至发生故障或烧毁。谐波可 引起电力系统局部并联谐振或串联谐振，使谐波含量放大，造成电容器等设备烧 毁。谐波还会引起继电保护和自动装置误动作，使电能计量出现混乱。对于电力 系统外部，谐波对通信设备和电子设备会产生严重干扰。 二、引言 谐波和间谐波测量是谐波问题中的一个重要分支，也是分析和治理谐波问题的出 发点和主要依据。谐波测量的主要作用有［２］：①鉴定实际电力系统和谐波源 用户的谐波水平是否符合标准的规定；②用于谐波源设备和其他电气设备调试、 投运时的 测量，以确保设备投运后电力系统和设备的安全经济运行；③谐波故 障 的 诊断；④提供实时补偿设备有源电力滤波器（ＡＰＦ）等）补偿的依据 等。考虑到真实电网信号固有的随机性和非平稳性，谐波和间谐波实时精确检测 至今仍是电能质量测试技术的难点和热点之一，随着计算机及微处理器的广泛应 用，数字技术在这一领域被越来越多采用，出现了 FFT 离散傅立叶变换的快速算 法，目前电力系统的谐波分析大多都是采用傅里叶分析实现的。 三、FFT FFT 是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号 在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征 了。这就是很多信号分析采用 FFT 变换的原因。另外，FFT 可以将一个信号的频 谱提取出来，这在频谱分析方面也是经常用的。 一个模拟信号，经过 ADC 采样 之后，就变成了数字信号。采样定理告诉我们，采样频率要大于信号频率的两倍， 采样得到的数字信号，就可以做 FFT 变换了。N 个采样点，经过 FFT 之后，就可 以得到 N 个点的 FFT 结果。为了方便进行 FFT 运算，通常 N 取 2 的整数次方。 假设采样频率为 Fs，信号频率 F，采样点数为 N。那么 FFT 之后结果就是一 个为 N 点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率 值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为 A，那么 FFT 的结果的每个点（除了第一个点直流分量之外）的模值就是 A 的 N/2 倍。而第一个点就是直流分量，它的模值就是直流分量的 N 倍。而每个点的相 位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即 0Hz），而最 后一个点 N 的再下一个点（实际上这个点是不存在的，这里是假设的第 N+1 个 点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率 Fs，这中间被 N-1 个点平均分成 N 等份，每个点的频率依次增加。例如某点 n 所 表示的频率为：Fn=(n-1)*Fs/N。由上面的公式可以看出，Fn 所能分辨到频率为为 Fs/N，如果采样频率 Fs 为 1024Hz，采样点数为 1024 点，则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点，刚好是 1 秒，也就是说，采样 1 秒时间的信号并做 FFT，
    则结果可以分析到 1Hz，如果采样 2 秒时间的信号并做 FFT，则结果可以分析到 0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分 辨率和采样时间是倒数关系。 假设 FFT 之后某点 n 用复数 a+bi 表示，那么这个复数的模就是 An=根号 a*a+b*b，相位就是 Pn=atan2(b,a)。根据以上的结果，就可以计算出 n 点（n≠1， 且 n<=N/2）对应的信号的表达式为：An/(N/2)*cos(2*pi*Fn*t+Pn)（式一），即 2*An/N*cos(2*pi*Fn*t+Pn)。对于 n=1 点的信号，是直流分量，幅度即为 A1/N。 由于 FFT 结果的对称性，通常我们只使用前半部分的结果，即小于采样频率 一半的结果。 FFT 的优缺点：ＤＦＴ算法实用、稳定、有效，采用ＦＦＴ可以提高算法的实时 性；但是频率分辨率有限，对于临近的频率成分无法检测。 三、间谐波检测 间谐波以波形畸变为特征，属于稳态电能质量问题。传统的傅里叶变换可以 精确地检测出信号中的频率成分，但对分析窗口宽度有严格要求。要达到检测间 谐波的成分的频率分辨率，就要采用较宽的 Fourier 变换窗口。实际从电力系统 中提取的电信号一般都含有噪声，这些噪声信号对于正确信息的处理是有害的。 对于包含间谐波的信号，每个相邻周期（基波周期）的信号可能不同，也就是说， 信号是变化的，当变化满足一定的规律时，比如说，每 N 个基波周期变化重复 一次。我们可以将 N 个基波周期视为一个周期，这样，信号就是周期信号了。 对该周期信号取 N 个基波周期进行傅里叶变换，可以得到下述表达式： （式二） 其中： 当 bm≥0 时， 当 bm<0 时，
    ω1 为基波角频率，ω1=2πf1，f1 为基波频率，T1=1/f1 为基波周期。 Tw 为傅里叶时间窗的宽度（持续时间），Tw=NT1。 c0 为直流分量。 cm 为频率 fm=mf1/N 的正弦分量的幅值。当 m/N 为整数时，该正弦分量为 称为谐波，当当 m/N 为非整数时，该正弦分量称为分数次谐波，也就是间谐波。 五、Matlab 仿真 5.1 Matlab 简介 大部分程序在处理高阶微分方程和大规模的联立方程组的问题时大量的时间和 精力都花在矩阵处理和图形的生成分析等繁琐易错的细节上。而 MATLAB 凭借其 强大的矩阵运算能力、简便的绘图功能、可视化的仿真环境以及丰富的算法工具 箱，已成为科研和工程技术人员的有力开发工具。MATLAB 包含大量计算算法的 集合。其拥有 600 多个工程中要用到的数学运算函数，可以方便的实现用户所需 的各种计算功能。函数中所使用的算法都是科研和工程计算中的最新研究成果， 而且经过了各种优化和容错处理。在通常情况下，可以用它来代替底层编程语言， 如 C 和 C++ 。在计算要求相同的情况下，使用 MATLAB 的编程工作量会大大减 少。MATLAB 的这些函数集包括从最简单最基本的函数到诸如矩阵，特征向量、 快速傅立叶变换的复杂函数。函数所能解决的问题其大致包括矩阵运算和线性方 程组的求解、微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据 的统计分析、工程中的优化问题、稀疏矩阵运算、复数的各种运算、三角函数和 其他初等数学运算、多维数组操作以及建模动态仿真等。 5.2 分析步骤 假设我们有一个信号，它含有 2V 的直流分量，频率为 50Hz、相位为-30 度、 幅度为 3V 的交流信号，以及一个频率为 75Hz、相位为 90 度、幅度为 1.5V 的交 流信号。用数学表达式就是如下： S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)（式三) 式中 cos 参数为弧度，所以-30 度和 90 度要分别换算成弧度。我们以 256Hz 的采 样率对这个信号进行采样，总共采样 256 点。按照我们上面的分析，Fn=(n-1)*Fs/N， 我们可以知道，每两个点之间的间距就是 1Hz，第 n 个点的频率就是 n-1。我们 的信号有 3 个频率：0Hz、50Hz、75Hz，应该分别在第 1 个点、第 51 个点、第 76 个点上出现峰值，其它各点应该接近 0。 实现的程序框图如下： 置入交流信号 设置直流分量幅度
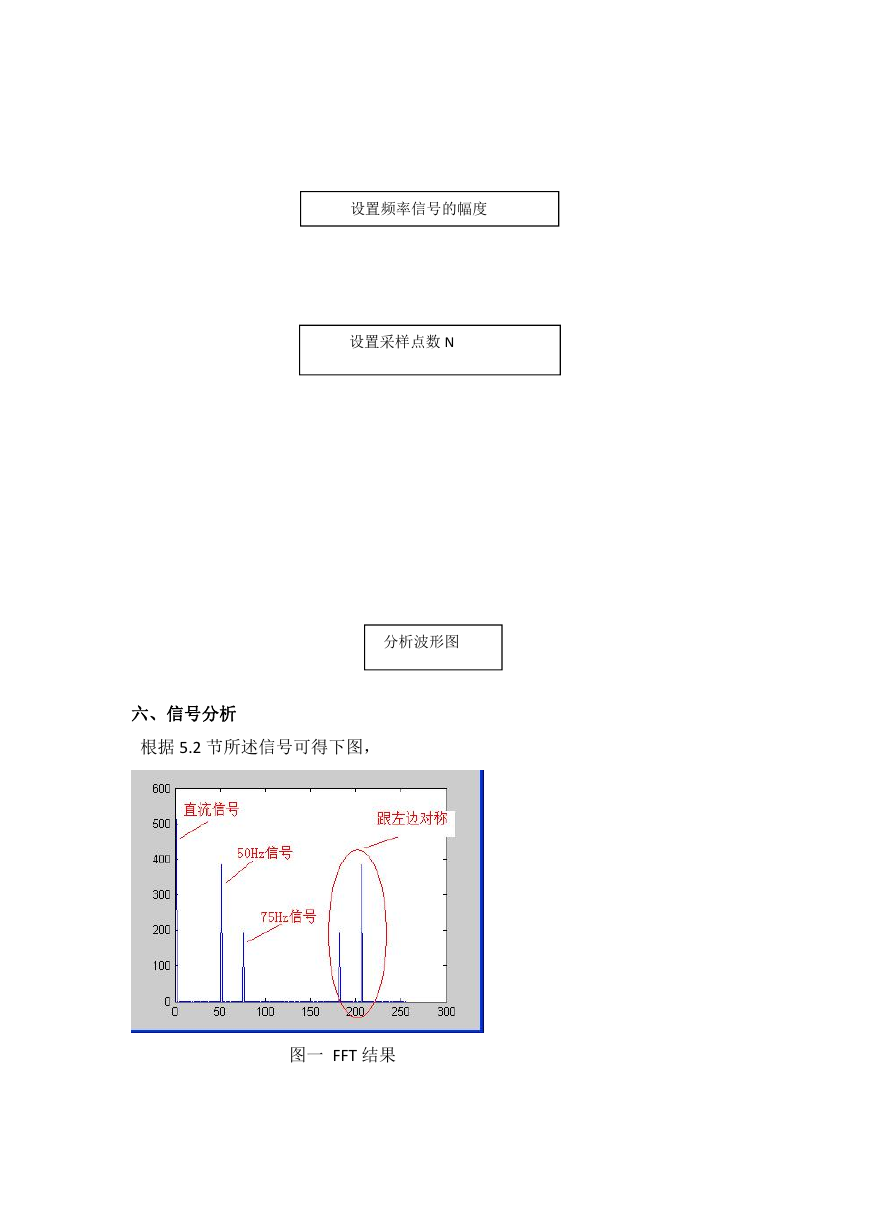
    设置频率信号的幅度 设置采样点数 N 分析波形图 六、信号分析 根据 5.2 节所述信号可得下图， 图一 FFT 结果
    从图一中我们可以看到，在第 1 点、第 51 点、和第 76 点附近有比较大的值。 我们分别将这三个点附近的数据拿上来细看： 1 点： 512+0i 2 点： -2.6195E-14 - 1.4162E-13i 3 点： -2.8586E-14 - 1.1898E-13i 50 点：-6.2076E-13 - 2.1713E-12i 51 点：332.55 - 192i 52 点：-1.6707E-12 - 1.5241E-12i 75 点：-2.2199E-13 -1.0076E-12i 76 点：3.4315E-12 + 192i 77 点：-3.0263E-14 +7.5609E-13i 很明显，1 点、51 点、76 点的值都比较大，它附近的点值都很小，可以认 为是 0，即在那些频率点上的信号幅度为 0。接着，我们来计算各点的幅度值。 分别计算这三个点的模值，结果如下： 1 点： 512 51 点：384 76 点：192 按照公式，可以计算出直流分量为：512/N=512/256=2；50Hz 信号的幅度为： 384/(N/2)=384/(256/2)=3；75Hz 信号的幅度为 192/(N/2)=192/(256/2)=1.5。可见， 从频谱分析出来的幅度是正确的。 然后再来计算相位信息。直流信号没有相位可言，不用管它。先计算 50Hz 信 号 的 相 位 ， atan2(-192, 332.55)=-0.5236, 结 果 是 弧 度 ， 换 算 为 角 度 就 是 180*(-0.5236)/pi=-30.0001 。 再 计 算 75Hz 信 号 的 相 位 ， atan2(192, 3.4315E-12)=1.5708 弧度，换算成角度就是 180*1.5708/pi=90.0002。可见，相位 也是对的。根据 FFT 结果以及上面的分析计算，我们就可以写出信号的表达式了， 它就是我们开始提供的信号。 七、结论 假设采样频率为 Fs，采样点数为 N，做 FFT 之后，某一点 n（n 从 1 开始）表示 的频率为：Fn=(n-1)*Fs/N；该点的模值除以 N/2 就是对应该频率下的信号的幅度 （对于直流信号是除以 N）；该点的相位即是对应该频率下的信号的相位。相位 的计算可用函数 atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值，范围从 -pi 到 pi。要精确到 xHz，则需要采样长度为 1/x 秒的信号，并做 FFT。要提高频 率分辨率，就需要增加采样点数，这在一些实际的应用中是不现实的，需要在较 短的时间内完成分析。解决这个问题的方法有频率细分法，比较简单的方法是采 样比较短时间的信号，然后在后面补充一定数量的 0，使其长度达到需要的点数， 再做 FFT，这在一定程度上能够提高频率分辨力。 参考文献： 【1】电力系统谐波和间谐波检测方法综述 熊杰锋，李群，袁晓冬，陈兵，杨志 超，王柏林
    【2】吕润馀．电力系统高次谐波［Ｍ］．北京：中国电力出版社，1998． 【3】戴先中，唐统一．周期信号谐波分析的一种新方法［Ｊ］．仪器仪表 学报. 【4】一种电网谐波与间谐波分析新方法 黄纯，朱智军，曹一家，汪沨，黎灿兵， 董旭柱. 【5】张伏生, 耿中行, 葛耀中. 电力系统谐波分析的高 精度 FFT 算法[J]. 附录 本测试数据使用的 Matlab 程序 close all; %先关闭所有图片 Adc=2; A1=3; %直流分量幅度 %频率 F1 信号的幅度 A2=1.5; %频率 F2 信号的幅度 F1=50; F2=75; %信号 1 频率(Hz) %信号 2 频率(Hz) Fs=256; %采样频率(Hz) P1=-30; %信号 1 相位(度) P2=90; N=256; %信号相位(度) %采样点数 t=[0:1/Fs:N/Fs]; %采样时刻 %信号
    S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180); %显示原始信号 plot(S); title('原始信号'); figure; Y = fft(S,N); %做 FFT 变换 Ayy = (abs(Y)); %取模 plot(Ayy(1:N)); %显示原始的 FFT 模值结果 title('FFT 模值'); figure; Ayy=Ayy/(N/2); %换算成实际的幅度 Ayy(1)=Ayy(1)/2; F=([1:N]-1)*Fs/N; %换算成实际的频率值 plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的 FFT 模值结果 title('幅度-频率曲线图'); figure; Pyy=[1:N/2]; for i=[1:N/2]; Pyy(i)=phase(Y(i)); %计算相位 Pyy(i)=Pyy(i)*180/pi; %换算为角度 end; plot(F(1:N/2),Pyy(1:N/2)); %显示相位图 title('相位-频率曲线图')
    分享到：
    赞 收藏

    相关推荐

    资料库

    信息化

    共收录1827份资料，累计6个分类，关注成员有19位，主要包括：管理软件,企业管理,电子商务,其它,IT管理,项目管理

    热门标签

    管理软件 企业管理 电子商务 其它 IT管理 项目管理

    最新资料