0-1背包问题之动态规划法_-.ppt

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：0.73M 资料格式：ppt 举报版权申诉

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第1页.png

第1页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第2页.png

第2页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第3页.png

第3页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第4页.png

第4页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第5页.png

第5页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第6页.png

第6页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第7页.png

第7页 / 共54页

1a3a7c30-33cf-418b-b545-b55c547a1fd5.ppt.pdf-第8页.png

第8页 / 共54页

文本预览

动态规划 1. 概述 2. 组合问题中的动态规划法 3. 图问题中的动态规划法 4. 查找问题中的动态规划法

1. 概述 1.1 例题（多段图） 1.2 什么是动态规划 1.3 动态规划适于解决什么样的问题 1.4 最优性原理 1.5 无后效性原则 1.6 动态规划法的设计思想

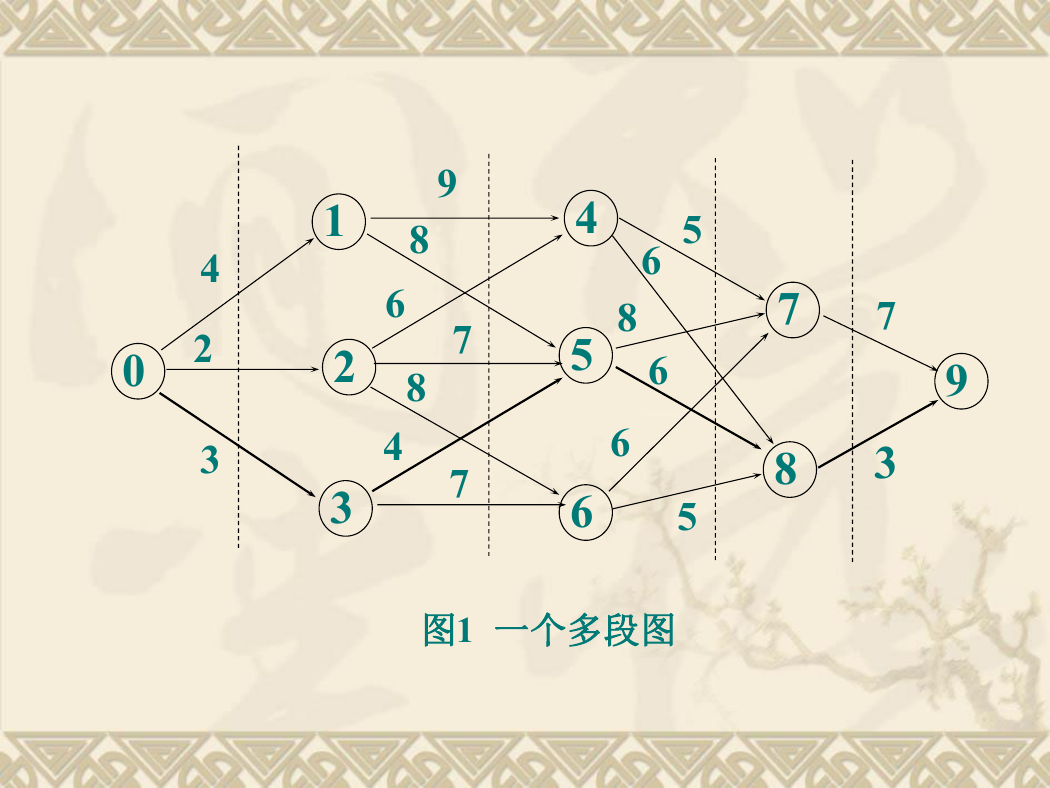
1.1 多段图的最短路径问题设图G=(V, E)是一个带权有向连通图，如果把顶点集合V划分成 k个互不相交的子集Vi（2≤k≤n, 1≤i≤k），使得E中的任何一条边(u, v)，必有u∈Vi，v∈Vi+m（1≤i＜k, 1＜i+m≤k），则称图G为多段图，称s∈V1为源点，t∈Vk为终点。多段图的最短路径问题是求从源点到终点的最小代价路径。由于多段图将顶点划分为k个互不相交的子集，所以，多段图划分为k段，每一段包含顶点的一个子集。根据多段图的定义，每个子集中的顶点互不邻接。不失一般性，将多段图的顶点按照段的顺序进行编号，同一段内顶点的相互顺序无关紧要。假设图中的顶点个数为n，则源点s的编号为0，终点t的编号为n-1，并且，对图中的任何一条边(u, v)，顶点u的编号小于顶点v的编号。

0 4 2 3 9 7 7 8 8 6 4 1 2 3 4 5 6 6 6 8 6 5 5 图1 一个多段图 7 8 7 3 9

设G是一个有向加权图，则G从顶点i到顶点j之间的最短路径问题满足最优性原理。证明：设i～ip～iq～j是一条最短路径，但其中子路径 ip～iq～j不是最优的，假设最优的路径为ip～iq’～j，则我们重新构造一条路径：i～ip～iq’～j 显然该路径长度小于i～ip～iq～j，与i～ip～iq～j 是顶点i到顶点j的最短路径相矛盾. 所以，原问题满足最优性原理。

对多段图的边(u, v)，用cuv表示边上的权值，将从源点s 到终点t的最短路径记为d(s, t)，则从源点0到终点9的最短路径d(0, 9)由下式确定： d(0, 9)=min{c01+d(1, 9), c02+d(2, 9), c03+d(3, 9)} 这是最后一个阶段的决策，它依赖于d(1, 9)、 d(2, 9)和d(3, 9)的计算结果，而 d(1, 9)=min{c14+d(4, 9), c15+d(5, 9)} d(2, 9)=min{c24+d(4, 9), c25+d(5, 9), c26+d(6, 9)} d(3, 9)=min{c35+d(5, 9), c36+d(6, 9)} 这一阶段的决策又依赖于d(4, 9)、d(5, 9)和d(6, 9) 的计算结果：

d(4, 9)=min{c47+d(7, 9), c48+d(8, 9)} d(5, 9)=min{c57+d(7, 9), c58+d(8, 9)} d(6, 9)=min{c67+d(7, 9), c68+d(8, 9)} 这一阶段的决策依赖于d(7, 9)和d(8, 9)的计算，而d(7, 9)和 d(8, 9)可以直接获得（括号中给出了决策产生的状态转移）： d(7, 9)=c79＝7(7→9) d(8, 9)=c89＝3(8→9) 再向前推导，有： d(6, 9)=min{c67+d(7, 9), c68+d(8, 9)}=min{6+7, 5+3}=8(6→8) d(5, 9)=min{c57+d(7, 9), c58+d(8, 9)}=min{8+7, 6+3}=9(5→8) d(4, 9)=min{c47+d(7, 9), c48+d(8, 9)}=min{5+7, 6+3}=9(4→8)

d(3, 9)=min{c 3 5+d(5, 9), c 3 6+d(6, 9)}=min{4+9, 7+8}=13(3→5) d(2, 9)=min{c24+d(4, 9), c25+d(5, 9), c26+d(6, 9)}=min{6+9, 7+9, 8+8}=15(2→4) d(1, 9)=min{c 1 4+d(4, 9), c 1 5+d(5, 9)}=min{9+9, 8+9}=17(1→5) d(0, 9)=min{c 0 1+d(1, 9), c 0 2+d(2, 9), c 0 3+d(3, 9)}=min{4+17, 2+15, 3+13}=16(0→3) 得到最短路径为0→3→5→8→9，长度为16。

分享到：

赞收藏

资料库

0-1背包问题之动态规划法_-.ppt

相关推荐

课程资源

热门标签

最新资料