数据结构课设报告之迷宫.docx

发布时间：2022-06-02 发布人：admin 分类：说明书资料大小：0.10M 资料格式：docx 举报版权申诉

第1页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第2页.png

第2页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第3页.png

第3页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第4页.png

第4页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第5页.png

第5页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第6页.png

第6页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第7页.png

第7页 / 共15页

qq_45772158-12616000-数据结构课设报告之迷宫.docx.pdf-第8页.png

第8页 / 共15页

三.概要设计

四．详细设计

数据结构课程设计报告设计题目：迷宫问题专学姓业号名 2020 年 6 月 22 日

一．问题描述设有一m 行 n 列迷宫，O 为可到达点，X 为不可到达点，F 为食物，S 为起点，E 为终点，有一小虫，想从 S 走到 E。该虫只能上、下、左、右四个方向移动，且不能出界。该虫最多能走k 步，当其走到 F 时，又可以走k 步。求从S 到 E 的最短“可行”路线. 二．需求分析在给定步数规则的限制下，从迷宫起点走向迷宫终点，并得到最短的路径。三.概要设计 1.节点结构体 struct { int i; // 横坐标int j; // 纵坐标int direction;//方向 }; //包含坐标与方向，坐标确定在数组中的位置，方向用来探索可走路径 2.求迷宫路径的基本思想框架首先选择利用堆栈来保存走过的节点，利用栈顶的节点对周围节点探索，如果有可走节点则入栈并标记为已走过节点，如果没有则退栈让该节点恢复为未走过，继续向四周探索，如此便可以发现可走的所有路径。 flag = 0; while (di < 4 && flag==0) { di++; switch (di)//四个方向寻找 { case 1:X = i + 1;Y = j ;break; case 2:X = i;Y = j - 1 ;break; case 3:X = i - 1;Y = j ;break; case 4:X = i;Y = j + 1 ;break; } if (a[X][Y] == o || a[X][Y] ==e || a[X][Y] == f )//如果为通路证明找到 { flag=1; } } if (flag) // 找到就修改原来栈顶的方向并且进栈新步骤 { Stack[top].direction = di; // 修改原栈顶元素的 di 值

top++;//入栈 } else // 否则将该点置为通路，退栈 { a[i][j] = o; top--; } 3.找到终点后先输出一下再与当前最短路径相对比如果小于或等于当前最小路径则保存到最小路径数组 static void one_path() { int k; cout <<"第"<< roadnumber++<<"条路："<< endl;// 输出第 roadnumber 条路径 for (k = 0; k <= top2; k++) { cout << "(" << minStack[k].i << "," << minStack[k].j << ")"; if (k != top2) cout << "->"; } cout << endl; if (top2 + 1 <=minlength) //找最短路径 { Path[minroadnumber][0].i= top2 + 1;//将路径长度存放在第一列的 i 中 for (k = 1; k <= top2+1; k++) //更新最短路径 { Path[minroadnumber][k].i = minStack[k-1].i; Path[minroadnumber][k].j = minStack[k-1].j; Path[minroadnumber][k].direction = minStack[k-1].direction; } minroadnumber++; minlength = top2 + 1; // 更新最短长度 } } 4.最后输出最短路径 static void min_path() { cout << "最短路径长度为：" << minlength << endl; cout << "路径为："<< endl; for (int k = 1; k <=minroadnumber; k++) { if (Path[k][0].i == minlength) { for (int l = 1; l <=minlength; l++)

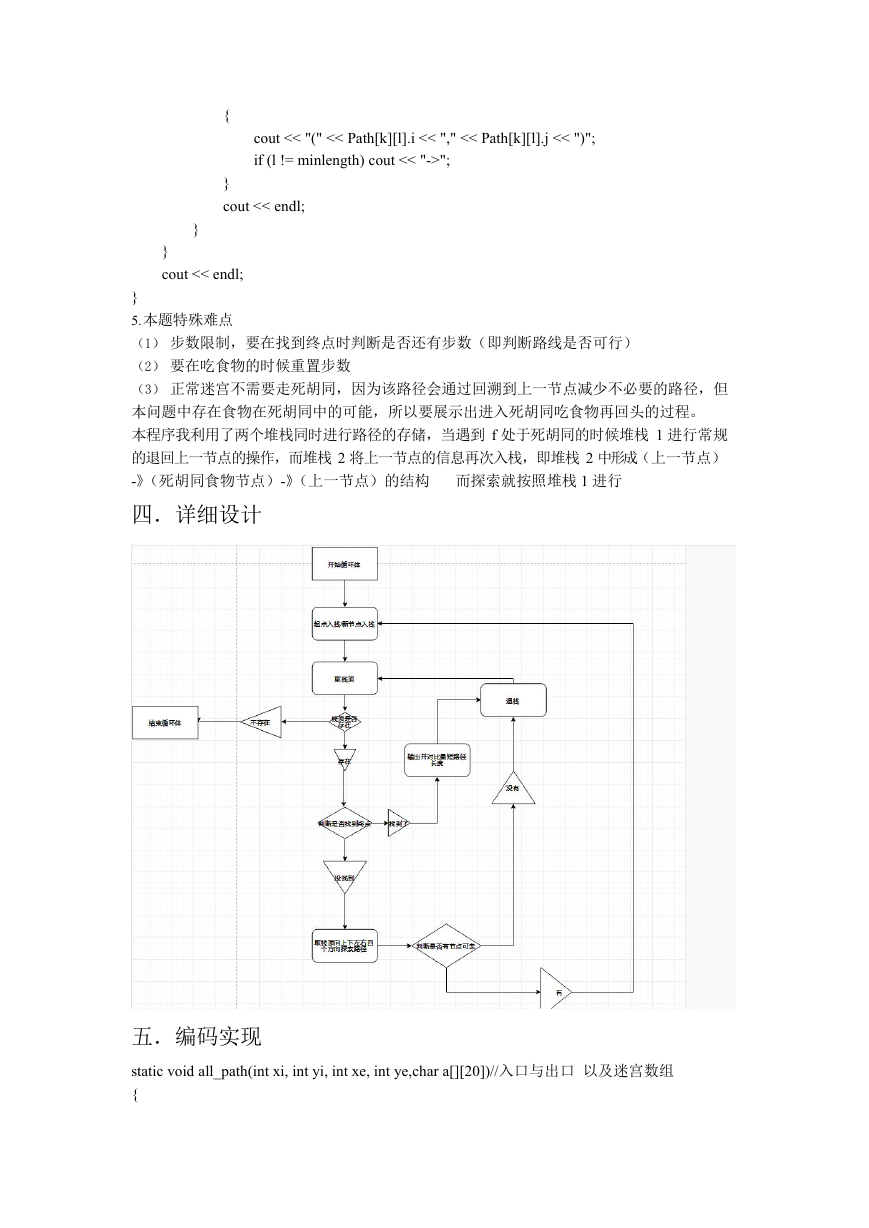
{ cout << "(" << Path[k][l].i << "," << Path[k][l].j << ")"; if (l != minlength) cout << "->"; } cout << endl; } } cout << endl; } 5.本题特殊难点（1）步数限制，要在找到终点时判断是否还有步数（即判断路线是否可行）（2）要在吃食物的时候重置步数（3）正常迷宫不需要走死胡同，因为该路径会通过回溯到上一节点减少不必要的路径，但本问题中存在食物在死胡同中的可能，所以要展示出进入死胡同吃食物再回头的过程。本程序我利用了两个堆栈同时进行路径的存储，当遇到 f 处于死胡同的时候堆栈 1 进行常规的退回上一节点的操作，而堆栈 2 将上一节点的信息再次入栈，即堆栈 2 中形成（上一节点） -》（死胡同食物节点）-》（上一节点）的结构而探索就按照堆栈 1 进行四．详细设计五．编码实现 static void all_path(int xi, int yi, int xe, int ye,char a[][20])//入口与出口以及迷宫数组 {

int i, j, di,X, Y,q,w,r; char o ='O'; char s ='S'; char e ='E'; char f ='F'; char p ='P'; char fp ='Q'; int flag = 0; top++; // 进栈 Stack[top].i = xi; Stack[top].j = yi; Stack[top].direction = 0;// 入口进栈 top2++; // 进栈 minStack[top2].i = xi; minStack[top2].j = yi; minStack[top2].direction = 0;// 入口进栈 a[xi][yi] = p; //标记为访问过 int find=0;//用来标志是否有路可走 while (top > -1) // 栈不空时循环 { i = Stack[top].i; j = Stack[top].j; di = Stack[top].direction;// 取栈顶 if (i == xe && j == ye && Step>0) // 找到终点 { one_path(); // 输出一条路径 find = 1;//代表有路 a[i][j] = e; // 让出口变为其他路径可走方块 top--; // 出口退栈 i = Stack[top].i; j = Stack[top].j; di = Stack[top].direction; // 更换栈顶 top2--; // 出口退栈 } flag = 0; while (di < 4 && flag==0) { di++; switch (di)//四个方向寻找 {case 1:X = i + 1;Y = j ;break; case 2:X = i;Y = j - 1 ;break; case 3:X = i - 1;Y = j ;break; case 4:X = i;Y = j + 1 ;break;

} if (a[X][Y] == o || a[X][Y] ==e || a[X][Y] == f )//如果为通路证明找到 { flag=1; } } if (flag) // 找到就修改原来栈顶的方向并且进栈新步骤 { Stack[top].direction = di; // 修改原栈顶元素的 di 值 minStack[top2].direction = di; top++;//入栈 top2++; if(a[X][Y] == f)//重置步数 { keepStep = Step; Step = 20; } else { Step--; (i1,j1)进栈 } Stack[top].i = X; Stack[top].j = Y; Stack[top].direction = 0; // 下一个可走方块 minStack[top2].i = X; minStack[top2].j = Y; minStack[top2].direction = 0; if(a[X][Y] == f) { a[X][Y]= fp;//遇到食物标记特殊的访问过 } else { } a[X][Y] = p; //标志为访问过

} else if(a[i][j]==fp)//堆栈 1 回溯到上一节点堆栈 2 入栈上一节点 { } top--; minStack[top2].direction = (Stack[top].direction+2)%4; top2++; minStack[top2].i = Stack[top].i; minStack[top2].j = Stack[top].j; minStack[top2].direction = Stack[top].direction; Step--; else // 否则将该点置为通路，退栈 { a[i][j] = o; top--; Step++; if(a[minStack[top2-1].i][minStack[top2-1].j]==fp)//提前监测是否退栈到食物位置如到达提前一格两次退栈 { a[minStack[top2-1].i][minStack[top2-1].j] = f; Step = keepStep; top2--; top2--; } top2--; } } if (find == 0) cout << "无路可走！" << endl; else { cout << "一共有" << roadnumber - 1 << "条路！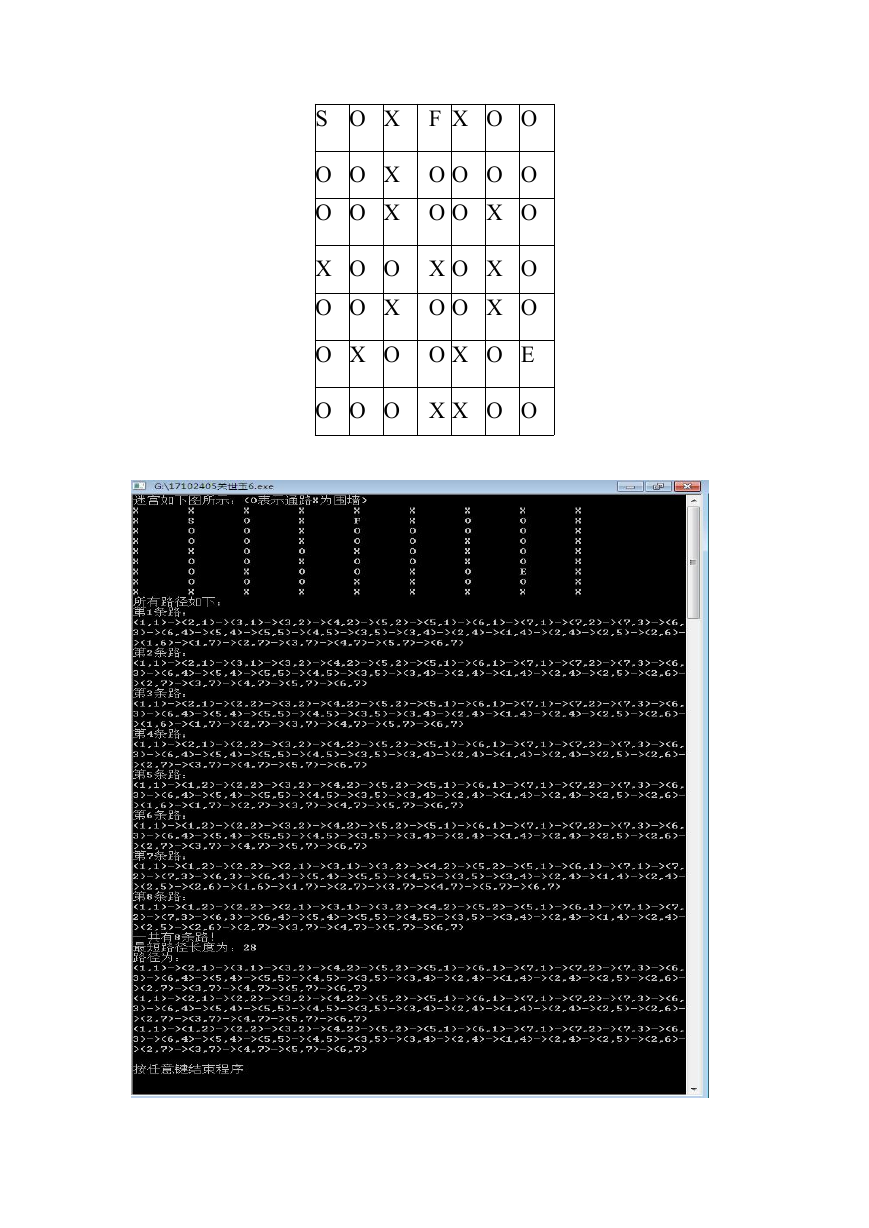" << endl; min_path(); // 输出最短路径 } } 六．实验结果与分析例如：m=7,n=7,k=20

S O X F X O O O O X O O O O O O X O O X O X O O X O X O O O X O O X O O X O O X O E O O O X X O O

分享到：

赞收藏

资料库

数据结构课设报告之迷宫.docx

相关推荐

行业

热门标签

最新资料