自动控制原理位置随动系统课程设计.doc-资料库

orangeyangchao-1945371--正文.doc.pdf-第1页.png

第1页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第2页.png

第2页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第3页.png

第3页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第4页.png

第4页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第5页.png

第5页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第6页.png

第6页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第7页.png

第7页 / 共13页

orangeyangchao-1945371--正文.doc.pdf-第8页.png

第8页 / 共13页

自动控制原理课程设计前言位置随动是指输出的位移随位置给定输入量而变化。在位置随动控制系统中，一般执行电动机常选用伺服电动机，所以也称位置私服控制系统。位置随动系统的应用十分广泛。如，军事工业中自动火炮跟踪雷达天线或跟踪电子望远镜的目标控制，陀螺仪的惯性导航控制，飞行器及火箭的飞行姿态控制；冶金工业中轧钢机轧辊压下装置的自动控制，按给定轨迹切割金属的火焰喷头的控制；仪器仪表工业中函数记录仪的控制以及机器人的自动控制等。一般来说，随动控制系统要求有好的跟随性能。位置随动系统是非常典型的随动系统，是个位置闭环反馈系统，系统中具有位置给定，位置检测和位置反馈环节，这种系统的各种参数都是连续变化的模拟量，其位置检测可用电位器、自整角机、旋转变压器、感应同步器等。位置随动系统中的给只给定量是经常变动的，是一个随机量，并要求输出量准确跟随给定量的变化，输出响应具有快速性、灵活性和准确性。为了保证系统的稳定性，并具有良好的动态性能，必须设有校正装置，如在正向通道中设置串联校正装并联校正装置等，为了提高位置随动系统的控制精度，还需要增加系统的开环放大倍数或在系统中增加积分环节等。 1

自整角机位置随动控制系统：顾耀国 1 设计原理及性能指标要求 1.1 设计原理要使角位移的输出量能够跟随给定角位移的输入量的变化而变化，达到位置随动的目的，可以通过位置的检测，反馈，校正等环节，形成位置闭环反馈系统。系统中具有位置给定，位置检测和位置反馈环节，这种系统的各种参数都是连续变化的模拟量，其位置检测可用电位器、自整角机、旋转变压器、感应同步器等。 1.2 设计性能指标根据现实需要，位置随动系统主要技术指标如下： (1)误差系数 C  0 ,0 1 C  /1( 200 ) s (2)单位阶跃响应的超调量 %3%  (3)单位阶跃响应的调节时间 ts 7.0 s (4)幅值裕度 ( dBh )  6 dB 通过对数学模型进行系统分析和动态校正，最后设计出一个符合稳定性、准确性和快速性要求的自整角机随动控制系统。 2 控制方案及系统组成原理方框图 2.1 控制方案要使角位移的输出量能够跟随给定角位移的输入量的变化而变化，达到位置随动的目的，可以通过位置的检测，反馈，校正等环节，形成位置闭环反馈系统。系统中具有位置给定，位置检测和位置反馈环节，这种系统的各种参数都是连续变化的模拟量，其位置检测可用电位器、自整角机、旋转变压器、感应同步器等。 1、自整角机用作测量机械转角（角位移）的传感器，是位置检测元件。随动系统通过一对自整角机来反映指令轴转角、执行轴转角和它们之间的角差，与指令轴相连的自整角机成为发送机，与执行轴相连的成为接收机。 2、相敏放大器用作将自整角机测角电路输出的角差电动势整流成直流信号，该信号不仅反映角差的大小，而且要反映角差的极性。 2

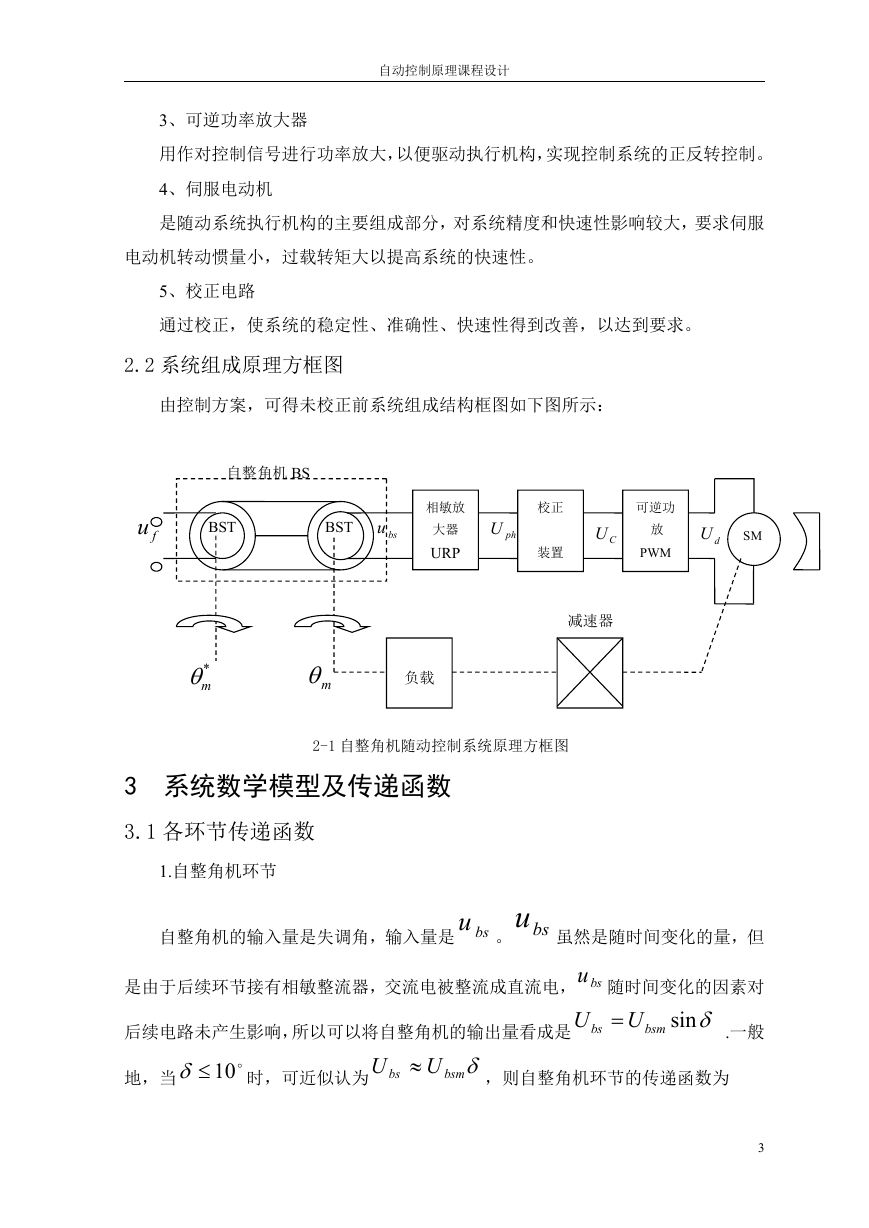
自动控制原理课程设计 3、可逆功率放大器用作对控制信号进行功率放大，以便驱动执行机构，实现控制系统的正反转控制。 4、伺服电动机是随动系统执行机构的主要组成部分，对系统精度和快速性影响较大，要求伺服电动机转动惯量小，过载转矩大以提高系统的快速性。 5、校正电路通过校正，使系统的稳定性、准确性、快速性得到改善，以达到要求。 2.2 系统组成原理方框图由控制方案，可得未校正前系统组成结构框图如下图所示：自整角机 BS fu BST BST bsu 相敏放大器 URP phU 校正装置 CU 可逆功放 PWM dU SM * m m 负载减速器 2-1 自整角机随动控制系统原理方框图 3 系统数学模型及传递函数 3.1 各环节传递函数 1.自整角机环节自整角机的输入量是失调角，输入量是 bsu 。 bsu 虽然是随时间变化的量，但是由于后续环节接有相敏整流器，交流电被整流成直流电， bsu 随时间变化的因素对后续电路未产生影响，所以可以将自整角机的输出量看成是 U  bs U bsm sin .一般地，当 10 时，可近似认为 U  bs U bsm ，则自整角机环节的传递函数为 3

自整角机位置随动控制系统：顾耀国  U bsm )( sUsW bs )( s  )(  bs 相敏整流环节相敏整流环节的输入量为自整角机的输出量 bsU ，输出量为相敏整流电压。该环节的滤波电路不仅对时间变量引起的电压波动有绿波作用，对由失调角 phU 的改变引起的电压波动也能够滤波。由于滤波环节只有一个储能元件，由 bsU 引起 phU 的变化是一阶惯性环节的响应，所以相敏整流环节的传递函数可由一阶惯性环节来描述，即 )( sW ph  ph )( sU )( sU bs  K ph sT  ph 1 式中， phK 为相敏整流放大器环节的放大倍数， apT 为阻容滤波时间常数。可逆功率放大器环节 PWM 可你功率放大器的输入量是 PWM 控制电路的控制电压 cU ，输出量是电动机的端电压 dU 。由于控制信号改变时，功率器件需经过一点延时才能体现出来，因而功率放大环节可以近似为一个小惯性环节，传递函数为 )( sW ap  式中， apK d  K ap sT  ap )( sU )( sU 为功率放大环节的放大倍数， apT 1 c 为延迟时间常数。执行电动机环节采用直流伺服电动机作为执行电动机，该环节的传递函数为 )( sW md  /1 C e 2 sT  m sTT lm  1 由于电动机的电磁时间常数比机电时间常数小一个数量级，可将电动机的传递函数近似为 4

自动控制原理课程设计 /1 C e 2 sT  m ( sTT lm   )1 ( sT m /1 C e )(1 sT  l  )1 减速机构环节减速机构的输入量是电动机的转速 n（单位是 r/min),输出量是拖动负载旋转的角度（单位是度）。输入输出的关系满足  m   n i 360 60 dt 6  i ndt 取零初始条件下的拉普拉斯变换，得到减速机构的传递函数为  6 is  K g s )( sW g  gK 式中， )( s  m )( sN 6 i  为减速机构环节的放大系数。可见，减速机构将转速变换为转角，是个积环节。采用串联校正时，校正装置可串接于乡民整流放大器与 PWM 控制电路之间。系统的动态结构图如图所示。图中， APRW s 为校正装置的传递函数。 ( ) 3.2 系统的动态结构图 * ( ) m s ( )s ( ) bsU s bsK — K ph T s  ph 1 ( ) phU s ( ) APRW s ( ) cU s ( ) dU s K ap T s  ap 1 /1 C e )(1 sT  l  )1 ( sT m ( ) m s gK s 图 3-1 位置随动系统动态结构图 5

自整角机位置随动控制系统：顾耀国 3.3 系统的开环传递函数 )( sG  ( sTs ph   式中， K obj  )(1 sT ap ( sTs ph CKKKK  / ap g bs ph e ap )(1 / g sT m CKKKK ph bs )(1 sT   ap K obj )(1  )(1 sT m sT l  e )(1 sT l )( sW APR  )1 )( sW APR  )1 4 系统稳态分析 4.1 系统的稳态分析位置随动系统稳定运行时，希望输出量能够准确地跟踪输入量，稳态误差却小越好。而在形成随动控制系统误差的诸多因素中，有些属于原理性误差，如系统结构和参数以及给定输入量引起的误差可以通过系统的校正设计加以抑制或消除，而有些属于非原理性误差，例如，检测误差和给定装置的误差靠校正是无法消除的，需要在设计时选用精密元件来加以限制。检测误差检测误差是由检测元件产生的，误差的大小取决于检测元件的精度。位置随动控制系统常用的检测元件有自整角机、旋转变压器、感应同步器、光电编码盘等，它们均有一定的准确度等级。各类检测元件也有准确度分级。不同检测元件的误差范围如表 4-1 所示（表中 N 指光电编码盘的栅缝数）表 4-1 几种检测元件的误差范围检测元件电位器自整角机误差范围角度级 1  旋转变压感应同步器器旋转式直线式角分级角秒级微米级光电码盘 360 N 6

自动控制原理课程设计原理误差原理误差是由系统结构和参数以及输入函数决定的稳态误差。图 3-1 所示位置随动系统的故有开环传递函数为 ' )( sG  ( sTs ph   ( sTs ph  )(1 g / ap )(1 sTssTT lm m ph  CKKKK bs e 2 )(1 sT ap K obj )(1 sTssTT  lm m  )1   2  )1 K obj  式中， CKKKK ap ph bs e sT ap / g 校正后系统的开环传递函数为 )( sWsGsG )( )(  ' APR  ( sTs ph sT ap APRW s 为位置调节器的传递函数。 ( ) )(1  式中， K obj )(1  sT m )( sW APR  )(1 sT l  )1 由自动控制原理知：选择比例调节器，则校正后的开环传递函数仍是 I 型系统，Ⅰ型系统只对位置输入信号是无静差的，对于速度输入能够跟踪，但有偏差，其偏差大小与系统的开环增益 K 成正比，并且由于积分环节位于系统的输出端，在积分环节之前，任何部位的阶跃扰动都将产生稳态误差，Ⅰ型系统不能够在加速度输入下工作。 Ⅱ型系统对位置输入和速度输入都是无差的，对于加速度输入也能跟踪，但有稳态误差，偏差大小与系统的开环增益成正比。与Ⅰ型系统相比，Ⅱ型系统比较理想，其稳态跟踪精度优于Ⅰ型系统。若设计成Ⅱ型系统，即要求位置调节器具有积分功能， ( ) APRW s 为 PI（或滞后网络）或 PID（或滞后超前网络）型调节器，这类调一般选节器传递函数的坟墓含有一个 S 的独立因子（或将大惯性环节近似为积分环节产生一个 s 独立因子）。按这样的传递函数设计系统，可使调节器后面前向通道中恒值扰动的稳态误差为 0。在有负载扰动时，负载扰动使Ⅰ型系统产生稳态误差，误差大小与负载扰动作用点以前的增益 K 成正比。而对型系统不产生稳态误差。从上述分析可以看出，Ⅱ型系统的跟踪能力和抗扰能力均比型系统优越。因此采 7

自整角机位置随动控制系统：顾耀国用Ⅱ型系统的结构比较合理。 5 系统的动态校正带入具体数值后系统的开环传递函数为： ( ) G s  s (0.1 s  1)(0.02 s  200 1)(0.01 s  1)(0.005 s  1) 5.1 绘出校正前的系统频率特性曲线绘出校正前的系统频率特性曲线如图 5-1 所示.由图知系统的性能指标未复合要求。 ) (L 60 40 20 0 -20 -40 -60 lg20 G 0 -40 -20 13 -40 50 10 0.13 0.1 1.3 1 Glg20 1000  100 200 -60 -80 -100 图 5-1 系统校正前和校正后的频率特性曲线根据性能指标要求，可以采用串联综合校正 5.2 串联综合校正先绘系统期望特性曲线： 1）期望特性曲线的低频段。低频段绘于图 5.1，起延长线在  200 rad / s 处于横 8

资料库

自动控制原理位置随动系统课程设计.doc

相关推荐

课程资源

热门标签

最新资料