第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
迭代学习控制的基本概念及应用.pdf
Iterative learning control (ILC) is based on the notion
that the performance of a system that executes the
same task multiple times can be improved by learning
from previous executions (trials, iterations, passes).
For instance, a basketball player shooting a free throw
from a fixed position can improve his or her ability to
score by practicing the shot repeatedly. During each shot,
the basketball player observes
the trajectory of the ball and
consciously plans an alteration
in the shooting motion for the
next attempt. As the player
continues to practice, the cor-
rect motion is learned and becomes ingrained into the
muscle memory so that the shooting accuracy is iteratively
improved. The converged muscle motion profile is an
open-loop control generated through repetition and learn-
ing. This type of learned open-loop control strategy is the
essence of ILC.
We consider learning controllers for systems that per-
form the same operation repeatedly and under the same
operating conditions. For such systems, a nonlearning con-
troller yields the same tracking error on each pass. Although
error signals from previous iterations are information rich,
they are unused by a nonlearning controller. The objective
of ILC is to improve performance by incorporating error
information into the control for subsequent iterations. In
doing so, high performance can be achieved with low tran-
sient tracking error despite large model uncertainty and
repeating disturbances.
ILC differs from other
learning-type control strate-
gies, such as adaptive control,
neural networks, and repeti-
tive control (RC). Adaptive
control strategies modify the controller, which is a system,
whereas ILC modifies the control input, which is a signal
[1]. Additionally, adaptive controllers typically do not take
advantage of the information contained in repetitive com-
mand signals. Similarly, neural network learning involves
the modification of controller parameters rather than a
control signal; in this case, large networks of nonlinear
neurons are modified. These large networks require exten-
sive training data, and fast convergence may be difficult to
DOUGLAS A. BRISTOW, MARINA THARAYIL,
and ANDREW G. ALLEYNE
© DIGITALVISION & ARTVILLE
A LEARNING-BASED METHOD
FOR HIGH-PERFORMANCE
TRACKING CONTROL
96 IEEE CONTROL SYSTEMS MAGAZINE » JUNE 2006
1066-033X/06/$20.00©2006IEEE
guarantee [2], whereas ILC usually converges adequately
in just a few iterations.
ILC is perhaps most similar to RC [3] except that RC is
intended for continuous operation, whereas ILC is intend-
ed for discontinuous operation. For example, an ILC appli-
cation might be to control a robot that performs a task,
returns to its home position, and comes to a rest before
repeating the task. On the other hand, an RC application
might be to control a hard disk drive’s read/write head, in
which each iteration is a full rotation of the disk, and the
next iteration immediately follows the current iteration.
The difference between RC and ILC is the setting of the ini-
tial conditions for each trial [4]. In ILC, the initial condi-
tions are set to the same value on each trial. In RC, the
initial conditions are set to the final conditions of the previ-
ous trial. The difference in initial-condition resetting leads
to different analysis techniques and results [4].
Traditionally, the focus of ILC has been on improving
the performance of systems that execute a single, repeated
operation. This focus includes many practical industrial
systems in manufacturing, robotics, and chemical process-
ing, where mass production on an assembly line entails
repetition. ILC has been successfully applied to industrial
robots [5]–[9], computer numerical control (CNC) machine
tools [10], wafer stage motion systems [11], injection-mold-
ing machines [12], [13], aluminum extruders [14], cold
rolling mills [15], induction motors [16], chain conveyor
systems [17], camless engine valves [18], autonomous vehi-
cles [19], antilock braking [20], rapid thermal processing
[21], [22], and semibatch chemical reactors [23].
ILC has also found application to systems that do not
have identical repetition. For instance, in [24] an underwa-
ter robot uses similar motions in all of its tasks but with
different task-dependent speeds. These motions are equal-
ized by a time-scale transformation, and a single ILC is
employed for all motions. ILC can also serve as a training
mechanism for open-loop control. This technique is used
in [25] for fast-indexed motion control of low-cost, highly
nonlinear actuators. As part of an identification procedure,
ILC is used in [26] to obtain the aerodynamic drag coeffi-
cient for a projectile. Finally, [27] proposes the use of ILC
to develop high-peak power microwave tubes.
The basic ideas of ILC can be found in a U.S. patent [28]
filed in 1967 as well as the 1978 journal publication [29]
written in Japanese. However, these ideas lay dormant
until a series of articles in 1984 [5], [30]–[32] sparked wide-
spread interest. Since then, the number of publications on
ILC has been growing rapidly, including two special issues
[33], [34], several books [1], [35]–[37], and two surveys [38],
[39], although these comparatively early surveys capture
only a fraction of the results available today.
As illustrated in “Iterative Learning Control Versus
Good Feedback and Feedforward Design,” ILC has clear
advantages for certain classes of problems but is not
applicable to every control scenario. The goal of the pre-
Iterative Learning Control Versus Good
Feedback and Feedforward Design
The goal of ILC is to generate a feedforward control that
tracks a specific reference or rejects a repeating distur-
bance. ILC has several advantages over a well-designed
feedback and feedforward controller. Foremost is that a feed-
back controller reacts to inputs and disturbances and, there-
fore, always has a lag in transient tracking. Feedforward
control can eliminate this lag, but only for known or measur-
able signals, such as the reference, and typically not for dis-
turbances. ILC is anticipatory and can compensate for
exogenous signals, such as repeating disturbances, in
advance by learning from previous iterations. ILC does not
require that the exogenous signals (references or distur-
bances) be known or measured, only that these signals
repeat from iteration to iteration.
While a feedback controller can accommodate variations
or uncertainties in the system model, a feedforward controller
performs well only to the extent that the system is accurately
known. Friction, unmodeled nonlinear behavior, and distur-
bances can limit the effectiveness of feedforward control.
Because ILC generates its open-loop control through prac-
tice (feedback in the iteration domain), this high-performance
control is also highly robust to system uncertainties. Indeed,
ILC is frequently designed assuming linear models and
applied to systems with nonlinearities yielding low tracking
errors, often on the order of the system resolution.
ILC cannot provide perfect tracking in every situation,
however. Most notably, noise and nonrepeating disturbances
hinder ILC performance. As with feedback control, observers
can be used to limit noise sensitivity, although only to the
extent to which the plant is known. However, unlike feedback
control, the iteration-to-iteration learning of ILC provides
opportunities for advanced filtering and signal processing.
For instance, zero-phase filtering [43], which is noncausal,
allows for high-frequency attenuation without introducing lag.
Note that these operations help to alleviate the sensitivity of
ILC to noise and nonrepeating disturbances. To reject nonre-
peating disturbances, a feedback controller used in combina-
tion with the ILC is the best approach.
sent article is to provide a tutorial that gives a complete
picture of the benefits, limitations, and open problems of
ILC. This presentation is intended to provide the practic-
ing engineer with the ability to design and analyze a sim-
ple ILC as well as provide the reader with sufficient
background and understanding to enter the field. As such,
the primary, but not exclusive, focus of this survey is on
single-input, single-output (SISO) discrete-time linear sys-
tems. ILC results for this class of systems are accessible
without extensive mathematical definitions and deriva-
tions. Additionally, ILC designs using discrete-time
JUNE 2006 « IEEE CONTROL SYSTEMS MAGAZINE 97
FIGURE 1 A two-dimensional, first-order ILC system. At the end of each iteration, the error is
filtered through L, added to the previous control, and filtered again through Q. This updated
open-loop control is applied to the plant in the next iteration.
Error
0
1
1
Control
Signal
0
0
1
j
j+1
Iteration
N−1
Sample
Time
+ +
Q
P
L
j
+
j+1
−
Disturbance Reference
Iteration
linearizations of nonlinear systems often yield good results
when applied to the nonlinear systems [10], [22], [40]–[43].
ITERATIVE LEARNING CONTROL OVERVIEW
Linear Iterative Learning Control
System Description
Consider the discrete-time, linear time-invariant (LTI),
SISO system
yj(k) = P(q)uj(k) + d(k),
(1)
where k is the time index, j is the iteration index, q is the
forward time-shift operator qx(k) ≡ x(k + 1), yj is the out-
put, uj is the control input, and d is an exogenous signal
that repeats each iteration. The plant P(q) is a proper ratio-
nal function of q and has a delay, or equivalently relative
degree, of m. We assume that P(q) is asymptotically stable.
When P(q) is not asymptotically stable, it can be stabilized
with a feedback controller, and the ILC can be applied to
the closed-loop system.
Next consider the N-sample sequence of inputs and
outputs
uj(k), k ∈ {0, 1, . . . , N − 1},
yj(k), k ∈ {m, m + 1, . . . , N + m − 1},
d(k), k ∈ {m, m + 1, . . . , N + m − 1},
and the desired system output
yd(k), k ∈ {m, m + 1, . . . , N + m − 1}.
The performance or error signal is defined by
ej(k) = yd(k) − yj(k). In practice, the time duration N of the
trial is always finite, although sometimes it is useful for
analysis and design to consider an infinite time duration of
98 IEEE CONTROL SYSTEMS MAGAZINE » JUNE 2006
N
Time
Sample
infinite
the trials [44]. In this work we use
N = ∞ to denote trials with an infi-
nite time duration. The iteration
dimension indexed by j is usually
considered
with
j ∈ {0, 1, 2, . . .}. For simplicity in this
article, unless stated otherwise, the
plant delay is assumed to be m = 1.
Discrete time is the natural
domain for ILC because ILC explicit-
ly requires the storage of past-itera-
tion data, which is typically
sampled. System (1) is sufficiently
general to capture IIR [11] and FIR
[45] plants P(q). Repeating distur-
bances [44], repeated nonzero initial
conditions [4], and systems aug-
mented with feedback and feedfor-
ward control [44] can be captured in
d(k). For instance, to incorporate the effect of repeated
nonzero initial conditions, consider the system
xj(k + 1) = Axj(k) + Buj(k)
yj(k) = Cxj(k),
(2)
(3)
with xj(0) = x0 for all j. This state-space system is equiv-
alent to
yj(k) = C(qI − A)−1B
uj(k) + CAkx0
.
P(q)
d(k)
Here, the signal d(k) is the free response of the system to
the initial condition x0.
A widely used ILC learning algorithm [1], [35], [38] is
uj+ 1(k) = Q(q)[uj(k) + L(q)ej(k + 1)],
(4)
where the LTI dynamics Q(q) and L(q) are defined as the
Q-filter and learning function, respectively. The two-
dimensional (2-D) ILC system with plant dynamics (1) and
learning dynamics (4) is shown in Figure 1.
General Iterative Learning Control Algorithms
There are several possible variations to the learning algo-
rithm (4). Some researchers consider algorithms with lin-
ear time-varying (LTV) functions [42], [46], [47], nonlinear
functions [37], and iteration-varying functions [1], [48].
Additionally, the order of the algorithm, that is, the num-
ber N0
and ei,
i ∈ { j− N0 + 1, . . . , j}, used to calculate uj+ 1 can be
increased. Algorithms with N0 > 1 are referred to as high-
er-order learning algorithms [26], [36], [37], [44], [49]–[51].
The current error ej+ 1 can also be used in calculating uj+ 1
iterations of ui
of previous
to obtain a current-iteration learning algorithm [52]–[56].
As shown in [57] and elsewhere in this article (see “Cur-
rent-Iteration Iterative Learning Control”), the current-iter-
ation learning algorithm is equivalent to the algorithm (4)
combined with a feedback controller on the plant.
Outline
The remainder of this article is divided into four major
sections. These are “System Representations,” “Analy-
sis,” “Design,” and “Implementation Example.” Time
and frequency-domain representations of the ILC sys-
tem are presented in the “System Representation” sec-
tion. The “Analysis” section examines the four basic
topics of greatest relevance to understanding ILC sys-
tem behavior: 1) stability, 2) performance, 3) transient
learning behavior, and 4) robustness. The “Design” sec-
tion investigates four different design methods: 1) PD
type, 2) plant inversion, 3) H∞, and 4) quadratically
optimal. The goal is to give the reader an array of tools
to use and the knowledge of when each is appropriate.
Finally, the design and implementation of an iterative
learning controller for microscale robotic deposition
manufacturing is presented in the “Implementation
Example” section. This manufacturing example gives a
quantitative evaluation of ILC benefits.
SYSTEM REPRESENTATIONS
Analytical results for ILC systems are developed using two
system representations. Before proceeding with the analy-
sis, we introduce these representations.
Time-Domain Analysis Using the
Lifted-System Framework
To construct the lifted-system representation, the rational
LTI plant (1) is first expanded as an infinite power series
by dividing its denominator into its numerator, yielding
P(q) = p1q
−1 + p2q
−2 + p3q
−3 + ··· ,
(5)
where the coefficients pk are Markov parameters [58].
is the impulse response. Note
The sequence p1, p2, . . .
that p1 = 0 since m = 1 is assumed. For the state space
description (2), (3), pk is given by pk = CAk−1B. Stack-
ing the signals in vectors, the system dynamics in (1)
can be written equivalently as the N × N-dimensional
lifted system
Current-Iteration Iterative Learning Control
Current-iteration ILC is a method for incorporating feedback with ILC [52]–[56]. The current-iteration ILC
algorithm is given by
uj+1(k ) = Q(q)[uj (k ) + L(q)ej (k + 1)] + C(q)ej+1(k )
and shown in Figure A. This learning scheme derives its name from the addition of a learning component in the current iteration
through the term C(q)ej+1(k). This algorithm, however, is identical to the algorithm (4) combined with a feedback controller in the
parallel architecture. Equivalence can be found between these two forms by separating the current-iteration ILC signal into feed-
forward and feedback components as
Feedback control
uj+1(k ) = wj+1(k ) + C(q)ej+1(k ),
where
wj+1(k) = Q(q)[uj (k) + L(q)ej (k + 1)].
Then, solving for the iteration-domain dynamic equation for
w yields
wj+1(k) = Q(q)[wj (k) + (L(q) + q
−1C(q))ej (k + 1)].
Therefore, the feedforward portion of the current-itera-
tion ILC is identical to the algorithm (4) with the learn-
ing function L(q) + q−1C(q). The algorithm (4) with
learning function L(q) + q−1C(q) combined with a
feedback controller in the parallel architecture is equiv-
alent to the complete current-iteration ILC.
Memory
L
Memory
ILC
Q
wj
uj
G
Plant
yj
yd
−
ej
C
Feedback
Controller
FIGURE A Current-iteration ILC architecture, which uses a control signal
consisting of both feedforward and feedback in its learning algorithm.
This architecture is equivalent to the algorithm (4) combined with a
feedback controller in the parallel architecture.
JUNE 2006 « IEEE CONTROL SYSTEMS MAGAZINE 99
=
yj(1)
yj(2)
...
yj(N)
yj
+
0
p1
p1
p2
...
...
pN pN−1
P
d(1)
d(2)
...
d(N)
,
···
···
. . .
···
0
0
...
p1
uj(0)
uj(1)
...
uj(N − 1)
uj
(6)
and
d
=
ej(1)
ej(2)
...
ej(N)
ej
−
.
yj(1)
yj(2)
...
yj(N)
yj
yd(1)
yd(2)
...
yd
yd(N)
The components of yj and d are shifted by one time step to
accommodate the one-step delay in the plant, ensuring
that the diagonal entries of P are nonzero. For a plant with
m-step delay, the lifted system representation is
=
yj(m)
yj(m + 1)
yj(m + N − 1)
ej(m)
ej(m + 1)
ej(m + N − 1)
...
...
=
=
×
−
···
···
. . .
···
0
0
...
pm
d(m)
d(m + 1)
...
d(m + N − 1)
,
pm
pm+1
...
pm+N−1
uj(0)
uj(1)
...
0
pm
...
pm+N−2
+
.
uj(N − 1)
yd(m)
yd(m + 1)
...
yd(m + N − 1)
yj(m)
yj(m + 1)
...
yj(m + N − 1)
The lifted form (6) allows us to write the SISO time- and
iteration-domain dynamic system (1) as a multiple-input,
multiple-output (MIMO) iteration-domain dynamic sys-
tem. The time-domain dynamics are contained in the struc-
ture of P, and the time signals uj, yj, and d are contained in
the vectors uj, yj, and d.
100 IEEE CONTROL SYSTEMS MAGAZINE » JUNE 2006
Likewise, the learning algorithm (4) can be written in
lifted form. The Q-filter and learning function can be non-
causal functions with the impulse responses
Q(q) = ··· + q−2q2 + q−1q1 + q0 + q1q
−1 + q2q
−2 + ···
and
L(q) = ··· + l−2q2 + l−1q1 + l0 + l1q
−1 + l2q
−2 + ··· ,
respectively. In lifted form, (4) becomes
uj+1(0)
uj+1(1)
...
uj+1
uj+1(N − 1)
q0
q1
...
qN−1
l0
l1
...
lN−1
+
uj
uj(0)
uj(1)
...
uj(N − 1)
.
ej(1)
ej(2)
...
ej(N)
ej
(7)
q−1
q0
...
qN−2
···
···
. . .
···
Q
q−(N−1)
q−(N−2)
...
q0
l−1
l0
...
lN−2
···
···
. . .
···
L
l−(N−1)
l−(N−2)
...
l0
When Q(q) and L(q) are causal functions, it follows that
q−1 = q−2 = ··· = 0 and l−1 = l−2 = ··· = 0, and thus the
matrices Q and L are lower triangular. Further distinctions
on system causality can be found in “Causal and Non-
causal Learning.”
The matrices P, Q, and L are Toeplitz [59], meaning that
all of the entries along each diagonal are identical. While
LTI systems are assumed here, the lifted framework can
easily accommodate an LTV plant, Q-filter, or learning
function [42], [60]. The construction for LTV systems is the
same, although P, Q, and L are not Toeplitz in this case.
k=0 x(k)z
Frequency-Domain Analysis Using the
z-Domain Representation
X(z) =∞
The one-sided z-transformation of the signal {x(k)}∞
k=0 is
−1, and the z-transformation of a system
is obtained by replacing q with z. The frequency response
of a z-domain system is given by replacing z with ei θ for
θ ∈ [−π, π]. For a sampled-data system, θ = π maps to the
Nyquist frequency. To apply the z-transformation to the ILC
system (1), (4), we must have N = ∞ because the
z-transform requires that signals be defined over an infi-
nite time horizon. Since all practical applications of ILC
have finite trial durations, the z-domain representation is
an approximation of the ILC system [44]. Therefore, for the
z-domain analysis we assume N = ∞, and we discuss
what can be inferred about the finite-duration ILC system
[44], [56], [61]–[64].
The transformed representations of the system in (1)
and learning algorithm in (4) are
Yj(z) = P(z)Uj(z) + D(z)
(8)
and
Uj+1(z) = Q(z)[Uj(z) + zL(z)Ej(z)],
(9)
respectively, where Ej(z) = Yd(z) − Yj(z). The z that multi-
plies L(z) emphasizes the forward time shift used in the learn-
ing. For an m time-step plant delay, zm is used instead of z.
ANALYSIS
Stability
The ILC system (1), (4) is asymptotically stable (AS) if there
exists ¯u ∈ R such that
|uj(k)| ≤ ¯u for all k = {0, . . . , N − 1} and j = {0, 1, . . . ,},
and, for all k ∈ {0, . . . , N − 1},
j→∞ uj(k) exists.
lim
We define the converged control as u∞(k) = limj→∞ uj(k).
Time-domain and frequency-domain conditions for AS of
the ILC system are presented here and developed in [44].
Substituting ej = yd − yj and the system dynamics (6)
into the learning algorithm (7) yields the closed-loop itera-
tion domain dynamics
uj+1 = Q(I − LP)uj + QL(yd − d).
(10)
Let ρ(A) = maxi |λi(A)| be the spectral radius of the matrix
A, and λi(A) the ith eigenvalue of A. The following AS
condition follows directly.
Theorem 1 [44]
The ILC system (1), (4) is AS if and only if
ρ(Q(I − LP)) < 1.
(11)
When the Q-filter and learning function are causal, the
matrix Q(I − LP) is lower triangular and Toeplitz with
repeated eigenvalues
In this case, (11) is equivalent to the scalar condition
|q0(1 − l0p1)| < 1.
(13)
Causal and Noncausal Learning
O ne advantage that ILC has over traditional feedback and
feedforward control is the possibility for ILC to anticipate
and preemptively respond to repeated disturbances. This
ability depends on the causality of the learning algorithm.
Definition: The learning algorithm (4) is causal if uj+1(k)
depends only on uj (h) and ej (h) for h ≤ k. It is noncausal if
uj+1(k) is also a function of uj (h) or ej (h) for some h > k.
Unlike the usual notion of noncausality, a noncausal
learning algorithm is implementable in practice because the
entire time sequence of data is available from all previous
iterations. Consider the noncausal learning algorithm
uj+1(k) = uj (k) + kpej (k + 1) and the causal learning algo-
rithm uj+1(k) = uj (k) + kpej (k). Recall that a disturbance d(k)
enters the error as ej (k) = yd(k) − P(q)uj (k) − d(k). There-
fore, the noncausal algorithm anticipates the disturbance
d(k + 1) and preemptively compensates with the control
uj+1(k). The causal algorithm does not anticipate since
uj+1(k) compensates for the disturbance d(k) with the same
time index k.
Causality also has implications in feedback equivalence
[63], [64], [111], [112], which means that the converged con-
trol u∞ obtained in ILC could be obtained instead by a feed-
back controller. The results in [63], [64], [111], [112] are for
continuous-time ILC, but can be extended to discrete-time
ILC. In a noise-free scenerio, [111] shows that there is feed-
back equivalence for causal learning algorithms, and further-
more that the equivalent feedback controller can be obtained
directly from the learning algorithm. This result suggests that
causal ILC algorithms have little value since the same control
action can be provided by a feedback controller without the
learning process. However, there are critical limitations to the
equivalence that may justify the continued examination and
use of causal ILC algorithms. For instance, the feedback
control equivalency discussed in [111] is limited to a noise-
free scenario. As the performance of the ILC increases, the
equivalent feedback controller has increasing gain [111]. In a
noisy environment, high-gain feedback can degrade perfor-
mance and damage equipment. Moreover, this equivalent
feedback controller may not be stable [63]. Therefore, causal
ILC algorithms are still of significant practical value.
When the learning algorithm is noncausal, the ILC does,
in general, preemptively respond to repeating disturbances.
Except for special cases, there is no equivalent feedback
controller that can provide the same control action as the
converged control of a noncausal ILC since feedback control
reacts to errors.
λ = q0(1 − l0p1).
(12)
JUNE 2006 « IEEE CONTROL SYSTEMS MAGAZINE 101
Using (8), (9), iteration domain dynamics for the
z-domain representation are given by
Uj+1(z) = Q(z) [1 − zL(z)P(z)] Uj(z)
+ zQ(z)L(z) [Yd(z) − D(z)] .
(14)
Many ILC algorithms are designed to converge to
zero error, e∞(k) = 0 for all k, independent of the refer-
ence or repeating disturbance. The following result
gives necessary and sufficient conditions for conver-
gence to zero error.
A sufficient condition for stability of the transformed sys-
tem can be obtained by requiring that Q(z)[1 − zL(z)P(z)]
be a contraction mapping. For a given z-domain system
T(z), we define T(z)∞ = supθ∈[−π,π]
Theorem 2 [44]
If
|T(eiθ )|.
Q(z)[1 − zL(z)P(z)]∞ < 1,
then the ILC system (1), (4) with N = ∞ is AS.
(15)
When Q(z) and L(z) are causal functions, (15) also
implies AS for the finite-duration ILC system [44], [52].
The stability condition (15) is only sufficient and, in gener-
al, much more conservative than the necessary and suffi-
cient condition (11) [4]. Additional stability results
developed in [44] can also be obtained from 2-D systems
theory [61], [65] of which ILC systems are a special case
[66]–[68].
Performance
The performance of an ILC system is based on the asymp-
totic value of the error. If the system is AS, the asymptotic
error is
e∞(k) = lim
j→∞ ej(k)
= lim
j→∞(yd(k) − P(q)uj(k) − d(k))
= yd(k) − P(q)u∞(k) − d(k).
Performance is often judged by comparing the difference
between the converged error e∞(k) and the initial error
e0(k) for a given reference trajectory. This comparison is
done either qualitatively [5], [12], [18], [22] or quantitatively
with a metric such as the root mean square (RMS) of the
error [43], [46], [69].
If the ILC system is AS, then the asymptotic error is
e∞ = [I − P[I − Q(I − LP)]
−1QL](yd − d)
(16)
for the lifted system and
E∞(z) =
1 − Q(z)
1 − Q(z)[1 − zL(z)P(z)]
[Yd(z) − D(z)]
(17)
for the z-domain system. These results are obtained by
replacing the iteration index j with ∞ in (6), (7) and (8), (9)
and solving for e∞ and E∞(z), respectively [1].
102 IEEE CONTROL SYSTEMS MAGAZINE » JUNE 2006
Theorem 3 [57]
Suppose P and L are not identically zero. Then, for the ILC
system (1), (4), e∞(k) = 0 for all k and for all yd and d, if
and only if the system is AS and Q(q) = 1.
Proof
See [57] for the time-domain case and, assuming N = ∞,
[11] for the frequency-domain case.
Many ILC algorithms set Q(q) = 1 and thus do not
include Q-filtering. Theorem 3 substantiates that this
approach is necessary for perfect tracking. Q-filtering,
however, can improve transient learning behavior and
robustness, as discussed later in this article.
More insight into the role of the Q-filter in performance
is offered in [70], where the Q-filter is assumed to be an
ideal lowpass filter with unity magnitude for low frequen-
cies [0, θc] and zero magnitude for high frequencies
θ ∈ (θc, π]. Although not realizable, the ideal lowpass filter
is useful here for illustrative purposes. From (17), E∞(ei θ )
for the ideal lowpass filter is equal to zero for θ ∈ [0, θc]
and equal to Yd(eiθ ) − D(eiθ ) for θ ∈ (θc, π]. Thus, for fre-
quencies at which the magnitude of the Q-filter is 1, perfect
tracking is achieved; for frequencies at which the magni-
tude is 0, the ILC is effectively turned off. Using this
approach, the Q-filter can be employed to determine which
frequencies are emphasized in the learning process.
Emphasizing certain frequency bands is useful for control-
ling the iteration domain transients associated with ILC, as
discussed in the “Robustness” section.
Transient Learning Behavior
We begin our discussion of transient learning behavior with
an example illustrating transient growth in ILC systems.
and
learning
Example 1
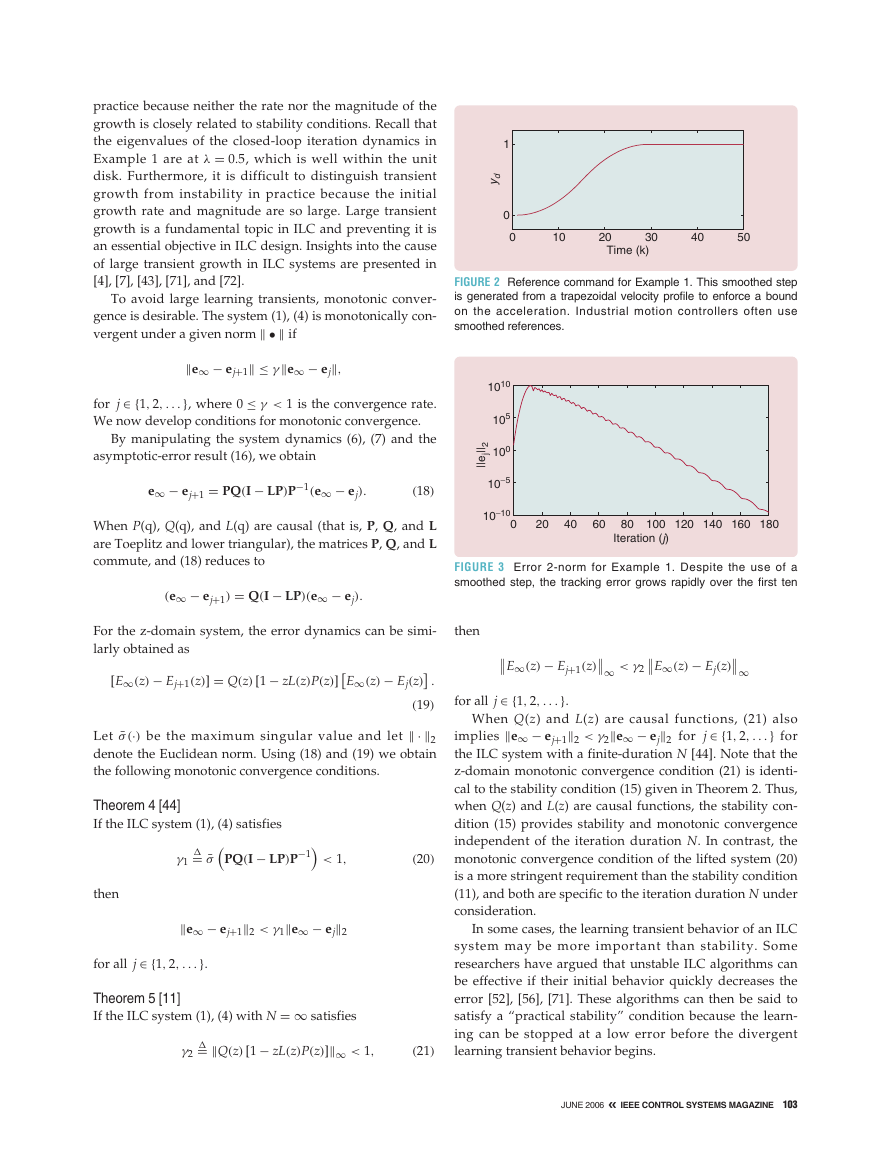
Consider the ILC system (1), (4) with plant dynamics
yj(k) = [q/(q − .9)2]uj(k)
algorithm
uj+1(k) = uj(k) + .5ej(k + 1). The leading Markov parame-
ters of this system are p1 = 1, q0 = 1, and l0 = 0.5. Since
Q(q) and L(q) are causal, all of the eigenvalues of the lifted
system are given by (12) as λ = 0.5. Therefore, the ILC
system is AS by Theorem 1. The converged error is identi-
cally zero because the Q-filter is unity. The trial duration is
set to N = 50, and the desired output is the smoothed-step
function shown in Figure 2. The 2-norm of ej is plotted in
Figure 3 for the first 180 trials. Over the first 12 iterations,
the error increases by nine orders of magnitude.
Example 1 shows the large transient growth that can
occur in ILC systems. Transient growth is problematic in
practice because neither the rate nor the magnitude of the
growth is closely related to stability conditions. Recall that
the eigenvalues of the closed-loop iteration dynamics in
Example 1 are at λ = 0.5, which is well within the unit
disk. Furthermore, it is difficult to distinguish transient
growth from instability in practice because the initial
growth rate and magnitude are so large. Large transient
growth is a fundamental topic in ILC and preventing it is
an essential objective in ILC design. Insights into the cause
of large transient growth in ILC systems are presented in
[4], [7], [43], [71], and [72].
To avoid large learning transients, monotonic conver-
gence is desirable. The system (1), (4) is monotonically con-
vergent under a given norm • if
e∞ − ej+1 ≤ γe∞ − ej,
for j ∈ {1, 2, . . .}, where 0 ≤ γ < 1 is the convergence rate.
We now develop conditions for monotonic convergence.
By manipulating the system dynamics (6), (7) and the
asymptotic-error result (16), we obtain
e∞ − ej+1 = PQ(I − LP)P
−1(e∞ − ej).
(18)
When P(q), Q(q), and L(q) are causal (that is, P, Q, and L
are Toeplitz and lower triangular), the matrices P, Q, and L
commute, and (18) reduces to
(e∞ − ej+1) = Q(I − LP)(e∞ − ej).
[E∞(z) − Ej+1(z)] = Q(z) [1 − zL(z)P(z)]
For the z-domain system, the error dynamics can be simi-
larly obtained as
E∞(z) − Ej(z)
(19)
Let ¯σ (·) be the maximum singular value and let · 2
denote the Euclidean norm. Using (18) and (19) we obtain
the following monotonic convergence conditions.
.
Theorem 4 [44]
If the ILC system (1), (4) satisfies
−1
PQ(I − LP)P
< 1,
(20)
= ¯σ
γ1
then
e∞ − ej+12 < γ1e∞ − ej2
for all j ∈ {1, 2, . . .}.
Theorem 5 [11]
If the ILC system (1), (4) with N = ∞ satisfies
= Q(z) [1 − zL(z)P(z)]∞ < 1,
γ2
(21)
d
y
1
0
0
10
20
30
40
50
Time (k)
FIGURE 2 Reference command for Example 1. This smoothed step
is generated from a trapezoidal velocity profile to enforce a bound
on the acceleration. Industrial motion controllers often use
smoothed references.
1010
105
100
2
|
|
j
e
|
|
10−5
10−10
0
20
40
60
80 100 120 140 160 180
Iteration (j)
FIGURE 3 Error 2-norm for Example 1. Despite the use of a
smoothed step, the tracking error grows rapidly over the first ten
then
E∞(z) − Ej+1(z)
∞ < γ2
E∞(z) − Ej(z)
∞
for all j ∈ {1, 2, . . .}.
When Q(z) and L(z) are causal functions, (21) also
implies e∞ − ej+12 < γ2e∞ − ej2 for j ∈ {1, 2, . . .} for
the ILC system with a finite-duration N [44]. Note that the
z-domain monotonic convergence condition (21) is identi-
cal to the stability condition (15) given in Theorem 2. Thus,
when Q(z) and L(z) are causal functions, the stability con-
dition (15) provides stability and monotonic convergence
independent of the iteration duration N. In contrast, the
monotonic convergence condition of the lifted system (20)
is a more stringent requirement than the stability condition
(11), and both are specific to the iteration duration N under
consideration.
In some cases, the learning transient behavior of an ILC
system may be more important than stability. Some
researchers have argued that unstable ILC algorithms can
be effective if their initial behavior quickly decreases the
error [52], [56], [71]. These algorithms can then be said to
satisfy a “practical stability” condition because the learn-
ing can be stopped at a low error before the divergent
learning transient behavior begins.
JUNE 2006 « IEEE CONTROL SYSTEMS MAGAZINE 103
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
