2020年山西运城中考数学试卷及答案.doc-资料库

第1页 / 共17页

第2页 / 共17页

第3页 / 共17页

第4页 / 共17页

第5页 / 共17页

第6页 / 共17页

第7页 / 共17页

第8页 / 共17页

2020 年山西运城中考数学试卷及答案第 I 卷选择题（共 30 分）一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑） 1．计算 A． 18  ( 6)     1 3    的结果是（） B． 2 C．18 D． 2 2．自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识．下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（） A． B． D． C ． 3．下列运算正确的是（） A． 3 a  2 a  2 5 a B． 28 a   4 a  2 a C ．   2 a 32   8 a 6 D． 3 a 4 2  3 a  12 a 6 4．下列几何体都是由 4 个大小相同的小正方体组成的，其中主视图与左视图相同的几何体是（） A． C ． B． D． 5．泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的（）

A．图形的平移 B．图形的旋转 C．图形的轴对称 D．图形的相似 6．不等式组 x 6 0 2        1 4 x  的解集是（） A． 5 x  B．3 x  5 C． 5 x  D． x   5 7．已知点  A x y ，  B x  , 1 1 , 2 y ，   2 C x y 都在反比例函数 , 3  3 y  k x  k  的图像上，且 0 x 1  x 2   ，则 1y ， 2y ， 3y 的大小关系是（） x 3 0 y A． 2  y 1  y 3 y B． 3  y 2  y 1 C ． y 1  y 2  y 3 y D． 3  y 1  y 2 8．中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花．图①中的摆盘，其形状是扇形的一部分，图 ② 是其几何示意图（阴影部分为摆盘），通过测量得到 AC BD   12 cm ，C ， D 两点之间的距离为 4cm ，圆心角为 60 ，则图中摆盘的面积是（）图①图② A． 80 cm 2 B． 40 cm 2 C． 24 cm 2 D． 2 cm 2 9．竖直上抛物体离地面的高度  h m 与运动时间    t s 之间的关系可以近似地用公式 h 5 t   2  v t h 0 0  表示，其中  0h m 是物体抛出时离地面的高度，   v m s 是物体抛出时 0 /  的速度．某人将一个小球从距地面1.5m 的高处以 20 /m s 的速度竖直向上抛出，小球达到的离地面的最大高度为（） A． 23.5m B． 22.5m C． 21.5m D． 20.5m 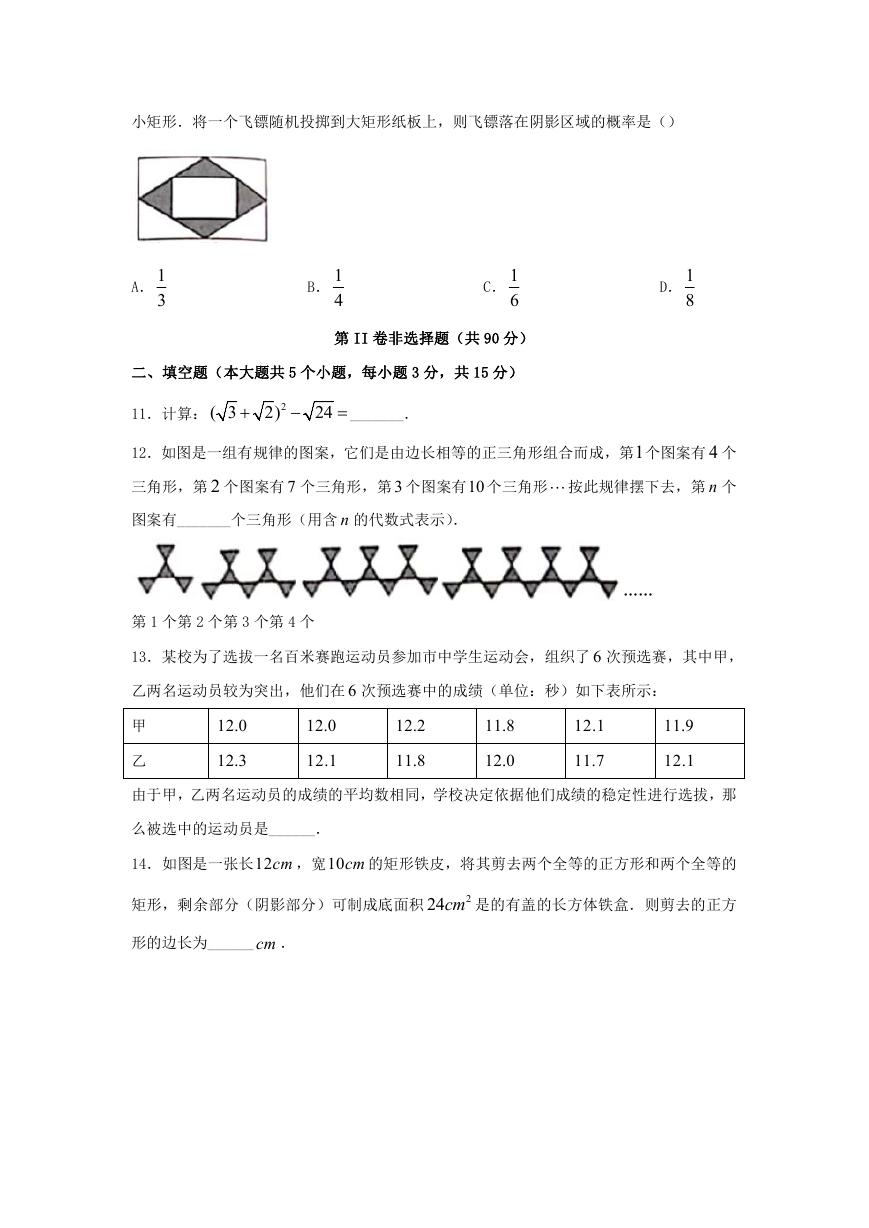10．如图是一张矩形纸板，顺次连接各边中点得到菱形，再顺次连接菱形各边中点得到一个

小矩形．将一个飞镖随机投掷到大矩形纸板上，则飞镖落在阴影区域的概率是（） A． 1 3 B． 1 4 C． 1 6 第 II 卷非选择题（共 90 分） D． 1 8 二、填空题（本大题共 5 个小题，每小题 3 分，共 15 分） 11．计算： ( 3  2 2)  24  _______． 12．如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有 4 个三角形，第 2 个图案有 7 个三角形，第 3 个图案有10 个三角形 按此规律摆下去，第 n 个图案有_______个三角形（用含 n 的代数式表示）． …… 第 1 个第 2 个第 3 个第 4 个 13．某校为了选拔一名百米赛跑运动员参加市中学生运动会，组织了 6 次预选赛，其中甲，乙两名运动员较为突出，他们在 6 次预选赛中的成绩（单位：秒）如下表所示：甲乙 12.0 12.3 12.0 12.1 12.2 11.8 11.8 12.0 12.1 11.7 11.9 12.1 由于甲，乙两名运动员的成绩的平均数相同，学校决定依据他们成绩的稳定性进行选拔，那么被选中的运动员是______． 14．如图是一张长12cm ，宽10cm 的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积 24cm 是的有盖的长方体铁盒．则剪去的正方 2 形的边长为______ cm ．

15．如图，在 Rt ABC E 为 BC 的中点， AE 与CD 交于点 F ，则 DF 的长为_______． AC  ， ACB 中， 3  90  ， BC  ，CD AB 4 ，垂足为 D ，三、解答题（本大题共 8 个小题，共 75 分．解答应写出文字说明，证明过程或演算步骤） 16．（1）计算： 2 ( 4)       3 1 2       ( 4 1) （2）下面是小彬同学进行分式化简的过程，请认真阅读并完成相应任务． 2 x  9  6 x  9  2 x 2 x   1 6 2 x ( x  3)(  ( x  x  2 3) 3)  2 2( x x   1 3) 第一步     x x   3 3  2 2( x x   1 3) 第二步 2( 2( x x   3) 3)  2 2( x x   1 3) 第三步 2 x 6 (2 x   2( 3) x   1) 第四步 2 x 6 2 x   2( 3) x   1 第五步   5 6x  2 第六步

任务一：填空： ① 以上化简步骤中，第 _____ 步是进行分式的通分，通分的依据是 ____________________或填为_____________________________； ② 第 _____ 步开始出现错误，这一步错误的原因是 _____________________________________；任务二：请直接写出该分式化简后的正确结果；任务三：除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议． 17． 2020 年5 月份，省城太原开展了“活力太原·乐购晋阳”消费暖心活动，本次活动中的家电消费券单笔交易满 600 元立减128 元（每次只能使用一张）某品牌电饭煲按进价提高 50% 后标价，若按标价的八折销售，某顾客购买该电饭煲时，使用一张家电消费券后，又付现金568 元．求该电饭煲的进价． 18．如图，四边形 OABC 是平行四边形，以点 O 为圆心， OC 为半径的 O 与 AB 相切于点 B ，与 AO 相交于点 D ， AO 的延长线交 O 于点 E ，连接 EB 交OC 于点 F ，求 C 和 E 的度数． 19． 2020 年国家提出并部署了“新基建”项目，主要包含“特高压，城际高速铁路和城市轨道交通，5G 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩”等．《 2020 新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域（5G 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩）总体的人才与就业机会．下图是其中的一个统计图．请根据图中信息，解答下列问题：

（1）填空：图中 2020 年“新基建”七大领域预计投资规模的中位数是______亿元；（2）甲，乙两位待业人员，仅根据上面统计图中的数据，从五大细分领域中分别选择了“5G 基站建设”和“人工智能”作为自己的就业方向，请简要说明他们选择就业方向的理由各是什么；（3）小勇对“新基建”很感兴趣，他收集到了五大细分领域的图标，依次制成编号为W ， G ，D ，R ， X 的五张卡片（除编号和内容外，其余完全相同），将这五张卡片背面朝上，洗匀放好，从中随机抽取一张（不放回），再从中随机抽取一张．请用列表或画树状图的方法求抽到的两张卡片恰好是编号为W （5G 基站建设）和 R （人工智能）的概率． W G D R X 20．阅读与思考下面是小宇同学的数学日记，请仔细阅读并完成相应的任务． ×年×月×日星期日没有直角尺也能作出直角今天，我在书店一本书上看到下面材料：木工师傅有一块如图①所示的四边形木板，他已经在木板上画出一条裁割线 AB ，现根据木板的情况，要过 AB 上的一点 C ，作出 AB 的垂线，用锯子进行裁割，然而手头没有直角尺，怎么办呢？办法一：如图①，可利用一把有刻度的直尺在 AB 上量出 CD  30 cm ，然后分别以 D ， C 为圆心，以 50cm 与 40cm 为半径画圆弧，两弧相交于点 E ，作直线 CE ，则 DCE 为90 ．必

图① 办法二：如图②，可以取一根笔直的木棒，用铅笔在木棒上点出 M ， N 两点，然后把木棒斜放在木板上，使点 M 与点C 重合，用铅笔在木板上将点 N 对应的位置标记为点Q ，保持点 N 不动，将木棒绕点 N 旋转，使点 M 落在 AB 上，在木板上将点 M 对应的位置标记为点 R ．然后将 RQ 延长，在延长线上截取线段QS MN ，得到点 S ，作直线 SC ，则 RCS  90  ．图② 我有如下思考：以上两种办法依据的是什么数学原理呢？我还有什么办法不用直角尺也能作出垂线呢？ …… 任务：（1）填空；“办法一”依据的一个数学定理是_____________________________________；（2）根据“办法二”的操作过程，证明 RCS  90  ；（3）①尺规作图：请在图③的木板上，过点C 作出 AB 的垂线（在木板上保留作图痕迹，不写作法）； ②说明你的作法依据的数学定理或基本事实（写出一个即可） 21．图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形 ABC 和 DEF 是闸机的“圆弧翼”，两圆弧翼成轴对称， BC 和 EF 均垂，点 A 与点 D 在直于地面，扇形的圆心角  ，半径 BA ED  60 cm  ABC   DEF  28  同一水平线上，且它们之间的距离为10cm ．

图①图②   0.88 （ 1 ）求闸机通道的宽度，即 BC 与 EF 之间的距离（参考数据： sin 28 cos 28 （2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的 2 倍， 180 人的团队通过一个智能闸机口比通过一个人工检票口可节约 3 分钟，求一个智能闸机平， tan 28 0.53     0.47 ，）；均每分钟检票通过的人数． 22．综合与实践问题情境：如图①，点 E 为正方形 ABCD 内一点，转90 ，得到 CBE  （点 A 的对应点为点 C ），延长 AE 交CE 于点 F ，连接 DE ． AEB  90  ，将 Rt ABE  绕点 B 按顺时针方向旋猜想证明：图①图② （1）试判断四边形 BE FE 的形状，并说明理由；（2）如图②，若 DA DE ，请猜想线段CF 与 FE 的数量关系并加以证明；解决问题：（3）如图①，若 AB  ， 15 CF  ，请直接写出 DE 的长． 3 23．综合与探究如图，抛物线 y  21 x 4   与 x 轴交于 A ， B 两点（点 A 在点 B 的左侧），与 y 轴交于 3 x 点 C ．直线 l 与抛物线交于 A ， D 两点，与 y 轴交于点 E ，点 D 的坐标为 4, 3 ． 

资料库

2020年山西运城中考数学试卷及答案.doc

相关推荐

中考

热门标签

最新资料