中国科学技术大学软件学院《算法设计与分析》实验报告.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：1.20M 资料格式：pdf 举报版权申诉

yahehehe-6869559-4744302543399016254.pdf-第1页.png

第1页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第2页.png

第2页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第3页.png

第3页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第4页.png

第4页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第5页.png

第5页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第6页.png

第6页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第7页.png

第7页 / 共25页

yahehehe-6869559-4744302543399016254.pdf-第8页.png

第8页 / 共25页

文本预览

中国科学技术大学软件学院《算法设计与分析》实验报告姓名：丁飞学号： SG13225013 指导教师：张曙专业：软设 1 班

中国科学技术大学软件学院《算法设计与分析》实验报告一．练手题 1： 1.实验内容：整数划分类输入：每组输入是两个整数 n 和 k。(1 <= n <= 50, 1 <= k <= n) 输出：对于每组输入，请输出六行。第一行：将 n 划分成若干正整数之和的划分数。第二行：将 n 划分成 k 个正整数之和的划分数。第三行：将 n 划分成最大数不超过 k 的划分数。第四行：将 n 划分成若干奇正整数之和的划分数。第五行：将 n 划分成若干不同整数之和的划分数。第六行：打印一个空行。 Sample Input 5 2 Sample Output 7 2 3 3 3 2.实验环境：编码环境：Windows 7 + Eclipse Kepler + JDK1.7 代码示例：CSDN Blog 代码编辑器 3.实验分析：问题 1：将 n 划分成若干正整数之和的划分数。此问题可以转化为，将整数 n 划分为最大不超过 n 的若干个整数。则，参照问题 3 解题思路。 - 1 -

中国科学技术大学软件学院《算法设计与分析》实验报告问题 2：将 n 划分成 k 个正整数之和的划分数。此问题可分为三大类情况：情况 1：nk 又可划分为两种情况： 1.存在整数 1,则分配出一个 1,并继续将(n-1)划分给剩下的(k-1)个数； 2.不存在整数 1,则给 k 个数都先分配一个 1,而后再对这剩下的(n-k）划分成 k 个数；由此，不难推导出算法递归式为代码 1-1：问题 3：将 n 划分成最大数不超过 k 的划分数。此问题可分为四大类情况：情况 1：如果 n 或者 m 为 1，只有一种划分可能：{1}或{1,1,1....,1,1}；情况 2：如果 n

中国科学技术大学软件学院《算法设计与分析》实验报告不难推出递归式为：对于问题 1，使 n=m 即可。代码 1-2：问题 4：将 n 划分成若干奇正整数之和的划分数。此问题可由 fun1 变形而来, 只需保证对奇偶数做不同的跳转即可。当遇到偶数时：减 1 递归；当遇到奇数时：在 fun1 算法的基础上,更改相关-1 操作为-2, 保证奇数性质, 再做递归。不难得到递归式为： - 3 - else )1fun1()fun1(mn )1fun1( 1mn )fun1(1 mor 1n 1)fun1(n,m-n-m,mn,n-n,nn,m

中国科学技术大学软件学院《算法设计与分析》实验报告代码 1-3： - 4 - mn )fun4(mn )2fun4()fun4(mn )2fun4(1odd is meven is m )1fun4( odd isn mn )1fun4(mn )2fun4()fun4(odd is meven is m )1fun4(even isn 1mor 1n 1)fun4(n,nn,m-n-m,mn,n-n,m-n,n-n,m-n-m,mn,m-n,m

中国科学技术大学软件学院《算法设计与分析》实验报告问题 5：将 n 划分成若干不同整数之和的划分数。此问题可由问题 3 变形而来，即保证问题 3 算法中每次被调用形参 m 一定比前一次运算调用时小。不难推出递归式为：代码 1-4： - 5 - else )1fun3()1fun3(mn )fun3(mn )1fun3(1m/2*m)(1n 02n 1)fun3(n,m-n-m,m-n,nn,m-n,m

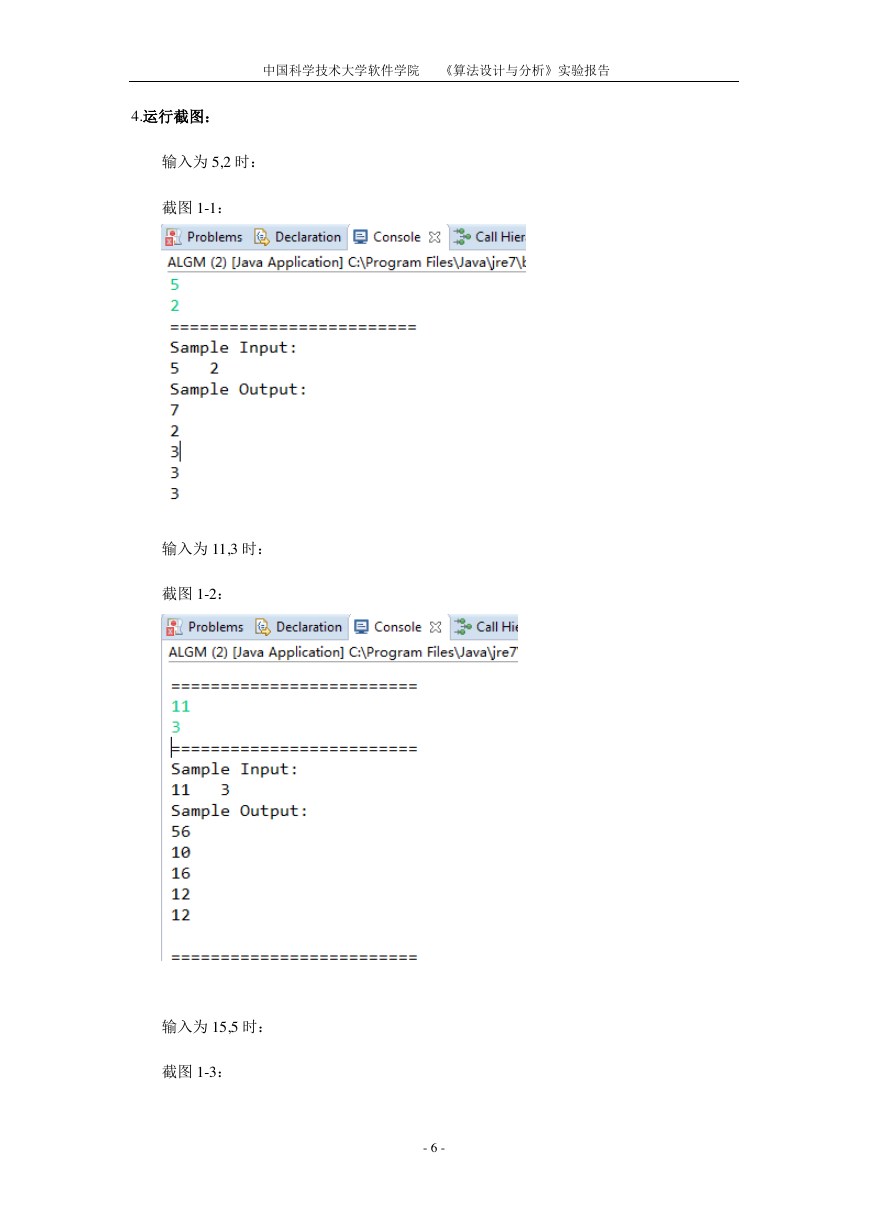
中国科学技术大学软件学院《算法设计与分析》实验报告 4.运行截图：输入为 5,2 时：截图 1-1：输入为 11,3 时：截图 1-2：输入为 15,5 时：截图 1-3： - 6 -

中国科学技术大学软件学院《算法设计与分析》实验报告 - 7 -

分享到：

赞收藏

资料库

中国科学技术大学软件学院《算法设计与分析》实验报告.pdf

相关推荐

课程资源

热门标签

最新资料