第1页 / 共1778页
第2页 / 共1778页
第3页 / 共1778页
第4页 / 共1778页
第5页 / 共1778页
第6页 / 共1778页
第7页 / 共1778页
第8页 / 共1778页
James Stewart 的 Calculus 第五版答案.pdf
Chapter 1
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Chapter 2
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Section 9
Chapter 3
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Section 9
Section 10
Section 11
Chapter 4
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Section 9
Section 10
Chapter 5
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Chapter 6
Section 1
Section 2
Section 3
Section 4
Section 5
Chapter 7
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Chapter 8
Section 1
Section 2
Section 3
Section 4
Section 5
Chapter 9
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Chapter 10
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Chapter 11
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Section 9
Section 10
Section 11
Section 12
Chapter 12
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Chapter 13
Section 1
Section 2
Section 3
Section 4
Chapter 14
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Chapter 15
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Section 9
Chapter 16
Section 1
Section 2
Section 3
Section 4
Section 5
Section 6
Section 7
Section 8
Section 9
Chapter 17
Section 1
Section 2
Section 3
Section 4
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
f (1)=2
.
, so
.
, we have
, so
is on the graph of
f
f (2) 2.8
y=2
are
2.8
y=2
x
)
(
1,2
1. (a) The point
(b) When
x=2 y
is about
,
(c)
is equivalent to
f (x)=2
(d) Reasonable estimates for
(e) The domain of
f
3 x 3
3,3
the range is
(f) As
.
increases from
2 y 3
, or
consists of all
. The range of
, or
1
x
2,3
.
increases from
3 y
to
,
x=3
. When
y=0
when
x
values on the graph of
consists of all
f
x=2.5
and
.
x=1
and
.
. For this function, the domain is
x=0.3
f
y
values on the graph of
f
. For this function,
2
to
3
. Thus,
f
is increasing on the interval
1,3
f (4)=2
. The point
3,4(
)
is on the graph of
g
, so
(
)
f
(
.
, so
4,2
f (x)=1
is on the graph of
)
2,1
is equivalent to
to
2. (a) The point
g(3)=4
(b) We are looking for the values of
x
2,2(
are equal at the points
(c)
. When
(d) As
decreases from
.
(e) The domain of
f
4 x 4
4,4
the range is
(f) The domain of
consists of all
. The range of
, or
2 y 3
is
and the range is
increases from
and
y=1
4 y
,
y=1
2,3
, or
0
.
g
x
4,3
0.5,4
.
for which the
)
, so the desired values of
y
y
values are equal. The
values for
.
2
and
x
f
and
g
, we have
1
to
x=3
. Thus,
3
and
2
are
x=4
.
f
is decreasing on the interval
0,4
x
values on the graph of
consists of all
f
f
. For this function, the domain is
y
values on the graph of
f
. For this function,
3. From Figure 1 in the text, the lowest point occurs at about
occurs at about
Figure 11, the range of the north south acceleration is approximately
210 a 200
the range of the east west acceleration is approximately
. Thus, the range of the vertical ground acceleration is
17,115
)= 12,85
t,a(
.
)
)
(
(
325 a 485
. The highest point
85 a 115
. In
. In Figure 12,
4. Example 1: A car is driven at
of the time . The domain of the function is
the function is
}
d |0 d 120
, where
d
mi h for
2
{
}
t |0 t 2
60
{
is measured in miles.
/
t
hours. The distance
d
traveled by the car is a function
, where is measured in hours. The range of
t
Example 2: At a certain university, the number of students
day is a function of the time after midnight. The domain of the function is
measured in hours. The range of the function is
largest number of students on campus at once.
}
N |0 N k
, where
N
N
{
t
on campus at any time on a particular
t
}
t |0 t 24
{
is an integer and is the
, where is
k
1
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
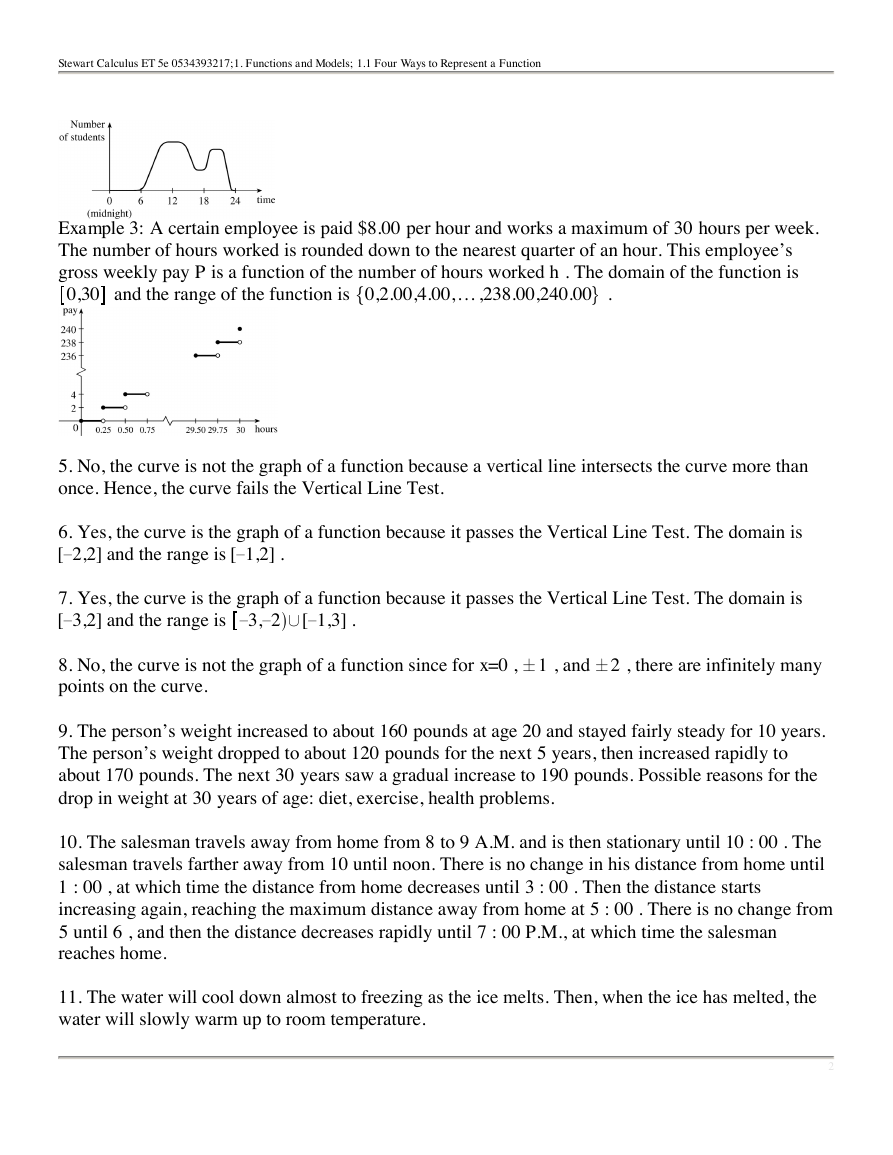
Example 3: A certain employee is paid
The number of hours worked is rounded down to the nearest quarter of an hour. This employee’s
. The domain of the function is
gross weekly pay
0,30
is a function of the number of hours worked
per hour and works a maximum of
and the range of the function is
}
0,2.00,4.00,... ,238.00,240.00
$8.00
hours per week.
30
P
{
h
.
5. No, the curve is not the graph of a function because a vertical line intersects the curve more than
once. Hence, the curve fails the Vertical Line Test.
6. Yes, the curve is the graph of a function because it passes the Vertical Line Test. The domain is
[2,2]
and the range is
[1,2]
.
7. Yes, the curve is the graph of a function because it passes the Vertical Line Test. The domain is
[3,2]
3,2) [1,3]
.
and the range is
8. No, the curve is not the graph of a function since for
points on the curve.
x=0 1
,
, and
2
, there are infinitely many
9. The person’s weight increased to about
120
The person’s weight dropped to about
about
drop in weight at
pounds. The next
170
30
30
pounds at age
160
20
and stayed fairly steady for
5
pounds for the next
years, then increased rapidly to
years saw a gradual increase to
190
pounds. Possible reasons for the
years.
10
years of age: diet, exercise, health problems.
, at which time the distance from home decreases until
10. The salesman travels away from home from
8
salesman travels farther away from
1 00
:
increasing again, reaching the maximum distance away from home at
5
until
6
reaches home.
, and then the distance decreases rapidly until
3 00
:
7 00
:
10
9
. The
until noon. There is no change in his distance from home until
A.M. and is then stationary until
10 00
to
:
. Then the distance starts
5 00
:
. There is no change from
P.M., at which time the salesman
11. The water will cool down almost to freezing as the ice melts. Then, when the ice has melted, the
water will slowly warm up to room temperature.
2
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
12. The summer solstice (the longest day of the year) is around June 21, and the winter solstice (the
shortest day) is around December 22.
13. Of course, this graph depends strongly on the geographical location!
14. The temperature of the pie would increase rapidly, level off to oven temperature, decrease rapidly,
and then level off to room temperature.
15.
16. (a)
(b)
(c)
3
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
(d)
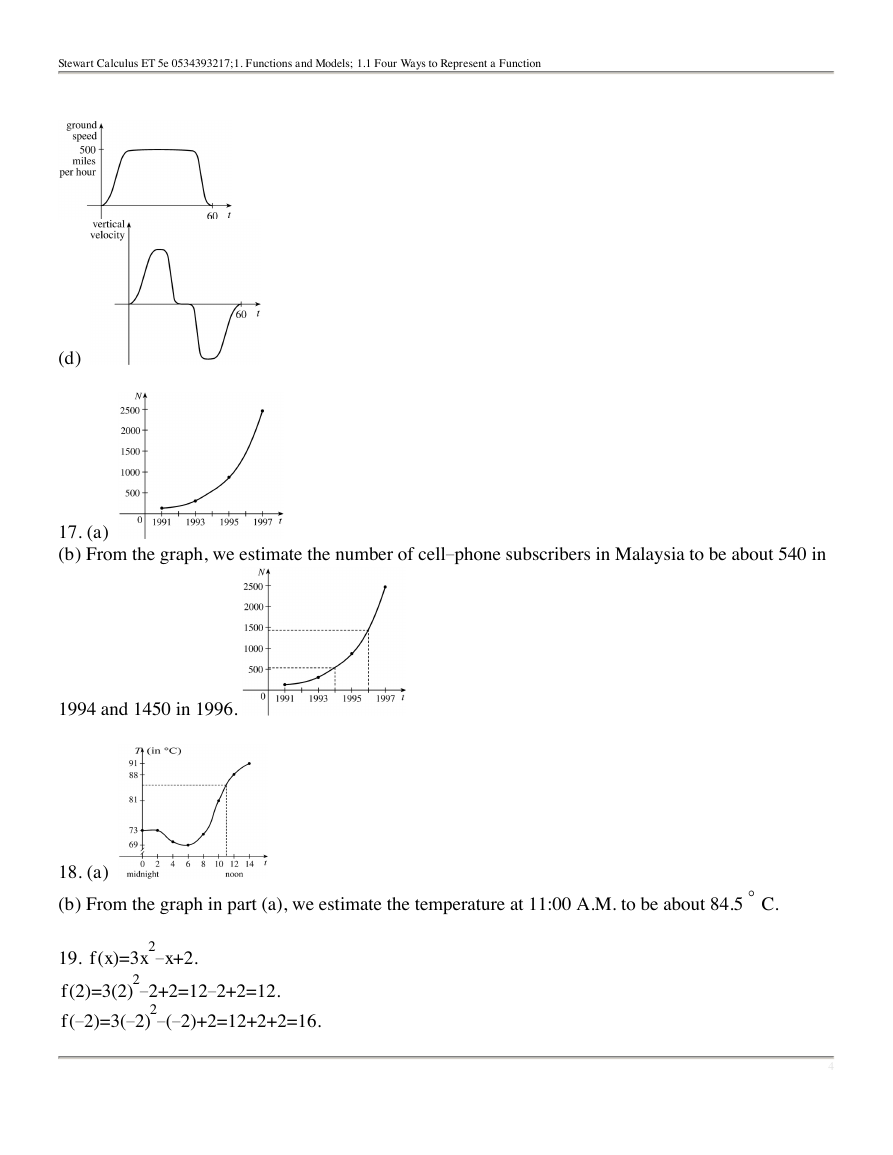
17. (a)
(b) From the graph, we estimate the number of cell phone subscribers in Malaysia to be about 540 in
1994 and 1450 in 1996.
18. (a)
(b) From the graph in part (a), we estimate the temperature at 11:00 A.M. to be about 84.5 C.
19.
f (x)=3x
f (2)=3(2)
f (2)=3(2)
2x+2.
22+2=122+2=12.
2(2)+2=12+2+2=16.
4
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
2a+2.
2(a)+2=3a
f (a)=3a
2
f (a)=3(a)
+a+2.
2(a+1)+2=3(a
2
2
2
+6a+3a+1=3a
+2a+1)a1+2=3a
f (a+1)=3(a+1)
+5a+4.
22a+4.
2a+2)=6a
2 f (a)=2f (a)=2(3a
2(2a)+2=3(4a
2
22a+2.
)2a+2=12a
f (2a)=3(2a)
2
2
4a
2
4
2
2
2(a
)a
+2.
+2=3a
)+2=3(a
)
)=3(a
f (a
) 3a
(
(
)
2
2a+2
2a+2
2a+2
2 = 3a
= 3a
22a+4=9a
43a
22a+6a
3
23a
3
46a
+a
+6a
=9a
2
2
2(a+h)+2=3(a
2
)ah+2=3a
+2ah+h
+6ah+3h
24a+4.
2ah+2.
f (a+h)=3(a+h)
3
+13a
f (a)
20. A spherical balloon with radius
(
4
3 r
wish to find the amount of air needed to inflate the balloon from a radius of to
r
4
3 r+1
has volume
V r+1
) 3
=
r+1
)=
(
(
(
)=
3
+3r
V r+1
) V r(
2
+3r+1
(
4
3 r
to find the difference
(
4
3 3r
(
2
2
2
2
)=2+h44hh
=2+h(4+4h+h
f (2+h)=2+h(2+h)
= h
+3h+2
, so
21.
2
2
) 2
2
22xhh
(
f (x+h)=x+h x+h
=x+h(x
)=x+hx
+2xh+h
, and
2
2x+x
22xhh
2
h(12xh)
h2xhh
x+hx
f (x+h)f (x)
2
f (x)=xx
2
+3r+1
4
3 r
)
3
=
r+1
)
.
)
,
=
h
h
=
=
h
=12xh
.
h
3
+3r
2
+3r+1
)
. We
. Hence, we need
22.
f (x)=
x
x+1
f (x+h)f (x)
h
=
, so
f (2+h)=
x
x+1
x+h
x+h+1
h
2+h
2+h+1
=
2+h
3+h
,
f (x+h)=
x+h
x+h+1
, and
(
=
x+h
) x+1
(
(
h x+h+1
) x x+h+1
) x+1
(
)
(
)
=
1
) x+1
(
x+h+1
)
(
.
23.
f (x)=x/(3x1)
is defined for all
x
except when
0=3x1 x=
1
3
, so the domain is
{
x R| x
1
3
} = ,
/
(
)
1
3
1
3
,
.
f (x)=(5x+4)
2
+3x+2
x
{
, so the domain is
24.
1
is defined for all
2
+3x+2 0=(x+2)(x+1) x=2
0=x
} =( ,2) (2,1) (1, )
.
except when
x
x R| x 2,1
25.
or
5
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
f (t)= t +3 t
value of gives a real number result for
is defined when
t 0
t
3 t
. The domain is
0, )
.
. These values of give real number results for
t
t
, whereas any
26.
g(u)= u + 4u
is defined when
u 0
and
4u 0 u 4
. Thus, the domain is
0 u 4= 0,4
.
4
/
h(x)=1
25x
x
27.
result in division by zero. The expression
methods for solving inequalities.) Thus, the domain is
is defined when
25x>0 x(x5)>0
x
x(x5)
. Note that
25x 0
x
x>5
. (See Appendix A for
or
( ,0) (5, )
.
is positive if
since that would
x<0
28.
. Now
2
h(x)= 4x
2 x
with center at the origin. The domain is
.
radius
2
From the graph, the range is
y= 4x
2
=4x
2 y
, or
0 y 2
0,2
2
2
+y
=4
{
x|4x
, so the graph is the top half of a circle of
2 0
} =[2,2]
.
} = x|4 x
} = x|2 x
{
{
2
f (x)=5
29.
horizontal line with
y
intercept
5
.
is defined for all real numbers, so the domain is
R
, or
( , )
. The graph of
f
is a
30.
F(x)=
is defined for all real numbers, so the domain is
R
, or
( , )
. The graph of
F
is
(x+3)
1
2
x
intercept
a line with
3
and
y
intercept
3
2
.
31.
f (t)=t
26t
is defined for all real numbers, so the domain is
R
, or
. The graph of
f
is a
parabola opening upward since the coefficient of
t
t
26t=t(t6) t=0
solve for .
t 0=t
and
t=6
is positive. To find the intercepts, let
and
t
. The coordinate of the vertex is halfway between the
6
y=0
2
( , )
t
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
intercepts, that is, at
t=3
. Since
f (3)=3
263=9
, the vertex is
(3,9)
.
32.
H(t)=
2
4t
2t
=
(2+t)(2t)
2t
the same as the graph of the function
f (t)=t+2
, so for
t 2 H(t)=2+t
,
. The domain is
}
t |t 2
(a line) except for the hole at
{
. So the graph of
2,4(
.
)
H
is
g(x)= x5
is defined when
33.
2
2
=x5 x=y
+5
y
, we see that
or
x 5
x5 0
is the top half of a parabola.
g
, so the domain is
5, )
. Since
y= x5
34.
F(x)= 2x+1 =
=
{
{
2x+1
(2x+1)
if 2x+1 0
if 2x+1<1
2x+1
2x1
1
if x
2
1
2
if x<
The domain is
R
, or
( , )
.
35.
7
Stewart Calculus ET 5e 0534393217;1. Functions and Models; 1.1 Four Ways to Represent a Function
G(x)=
3x+ x
x
. Since
x =
{
G(x)=
{
x
x
if x 0
if x<0
3x+x
x
3xx
x
if x>0
if x<0
, we have
{
=
4x
x
2x
x
if x>0
if x<0
{
=
4
2
if x>0
if x<0
Note that
G
is not defined for
x=0
. The domain is
( ,0) (0, )
.
36.
g(x)=
x
2
x
. Since
x =
{
g(x)=
x
x
{
if x 0
if x<0
, we have
x
2
x
x
2
x
if x>0
if x<0
{
=
1
x
1
x
if x>0
if x<0
Note that
g
is not defined for
x=0
. The domain is
( ,0) (0, )
.
37.
f (x)=
{
Domain is
R
x
x+1
, or
if x 0
if x>0
( , )
.
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
