遗传算法求解10城市的旅行商问题的c语言.doc

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.10M 资料格式：doc 举报版权申诉

第1页 / 共16页

第2页 / 共16页

第3页 / 共16页

第4页 / 共16页

第5页 / 共16页

第6页 / 共16页

第7页 / 共16页

第8页 / 共16页

文本预览

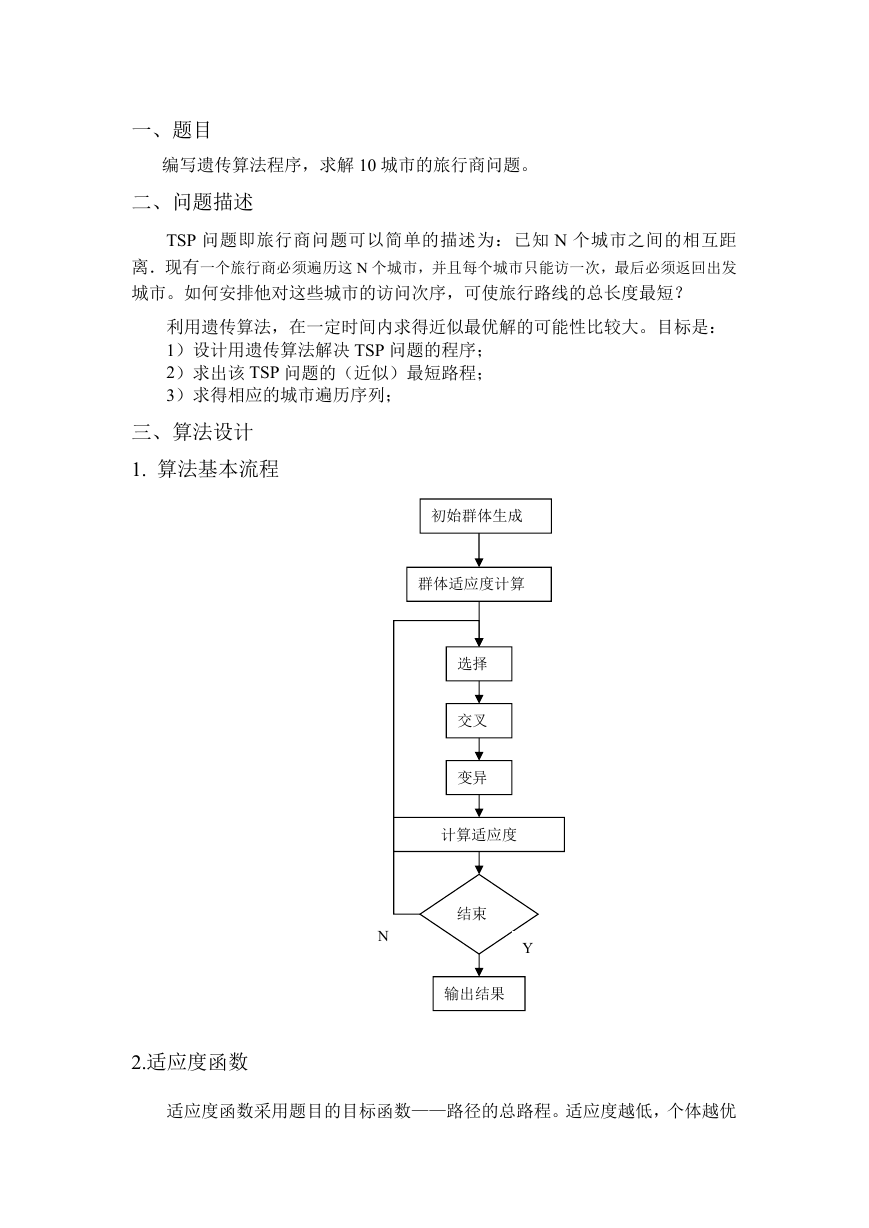
一、题目编写遗传算法程序，求解 10 城市的旅行商问题。二、问题描述 TSP 问题即旅行商问题可以简单的描述为：已知 N 个城市之间的相互距离．现有一个旅行商必须遍历这 N 个城市，并且每个城市只能访一次，最后必须返回出发城市。如何安排他对这些城市的访问次序，可使旅行路线的总长度最短？利用遗传算法，在一定时间内求得近似最优解的可能性比较大。目标是： 1）设计用遗传算法解决 TSP 问题的程序； 2）求出该 TSP 问题的（近似）最短路程； 3）求得相应的城市遍历序列；三、算法设计 1. 算法基本流程初始群体生成群体适应度计算选择交叉变异计算适应度 N 结束 Y 输出结果 2.适应度函数适应度函数采用题目的目标函数——路径的总路程。适应度越低，个体越优

秀。 3.选择算子在遗传个体的选择上，先人工保留最优种子，再采用轮盘赌法选择保留一部分个体，用轮盘赌法的理由是在“择优录取”的原则上增加选择的随机性。在轮盘赌过程中，如果按适应度来划分，将导致适应度高的劣质个体被选择的概率更大，于是设计了一个变换，用最坏适应度减去该个体的适应度，再进行轮盘赌选择。另外，为了保持群体的“生命力”，我们在选择的同时又引入随机的新个体，与保留的个体进行“杂交”，产生下一代。 4.交叉算子采用顺序交叉、双亲双子遗传的算法。随机选择两个交叉点 A 、 B （0 #include #include #include #include //能产生的路径总数 void init(FILE *fp); void lunpan(int count); int fab(int n); void ga(); double countTSP(int index); //求解各路径的总路程 void minTSP(int gen); void variant(); //变异 //遗传算法求解 //获取当前种群中最短的一条路径

void crossGA(); // 交叉变换 void choice(); //选择 void replace();//替换 void showinfor(); struct CityNode { int num; double x; double y; int reserved; }; struct CityLine { int general; CityNode *city[30];//30 为城市的最大规模 double sum; }; CityNode *city[30]; int n=0; CityLine *father[30],*fatherbest,*sontmp,*allbest,*choices[10];//30 为种群规模 double sum[30],min,variance=0.3,minall=0; //各个体的总路程变异概率为 0.3 FILE *result; void main() { FILE *fp; fp = fopen("city.txt","r"); result=fopen("result.txt","a"); if(fp==NULL) { printf("can not open file!"); return; } printf("......START......\n"); init(fp); fclose(fp); fclose(result); printf("......END......\n"); }

void init(FILE *fp) { int count; fseek(fp,0,1); sontmp=(CityLine *)malloc(sizeof(CityLine)); allbest=(CityLine *)malloc(sizeof(CityLine)); fatherbest=(CityLine *)malloc(sizeof(CityLine)); for(int ch=0;ch<10;ch++) choices[ch]=(CityLine *)malloc(sizeof(CityLine)); //读取文件数据初始化节点信息 while (!feof(fp)&&n<10) { city[n]=(CityNode *)malloc(sizeof(CityNode)); city[n]->num=n; fscanf(fp,"%lf %lf",&city[n]->x,&city[n]->y); printf("city[%d]->x=%lf city[%d]->y=%lf\n",n,city[n]->x,n,city[n]->y); fprintf(result,"city[%d]->x=%lf city[%d]->y=%lf\n",n,city[n]->x,n,city[n]->y); city[n]->reserved=0; n++; } count=fab(n); printf("%d\n",count); if(50>=count) { lunpan(count); } else { } ga(); } int fab(int n) { if(n==0 || n==1) return 1; else return n*fab(n-1); }

void lunpan(int count) { int r=0; srand(time(NULL)); //随机数种子 for(int i=0;igeneral=0; for(int k=0;kreserved=0; } for(int j=0;jreserved==0) { father[i]->city[j]=city[r]; city[r]->reserved=1; printf("%d \n",r); } else { //若节点已存在于个体重新选择其他新的节点 while(1) { r=(int)((double)rand() / ((double)RAND_MAX + 1) * n); if(city[r]->reserved==0) { father[i]->city[j]=city[r]; city[r]->reserved=1; printf("%d \n",r); break; } } } } sum[i]= countTSP(i); father[i]->sum=sum[i]; printf("%lf \n",sum[i]); }

} void ga() { //生成第一代种群 int r=0; srand(time(NULL)); for(int i=0;i<30;i++) { father[i]=(CityLine *)malloc(sizeof(CityLine)); father[i]->general=1; for(int k=0;kreserved=0; } for(int j=0;jreserved==0) { father[i]->city[j]=city[r]; city[r]->reserved=1; city[r]->num=r; ",r); printf("%d //若节点已存在于个体重新选择其他新的节点 while(1) { r=(int)((double)rand() / ((double)RAND_MAX + 1) * n); if(city[r]->reserved==0) { father[i]->city[j]=city[r]; city[r]->reserved=1; city[r]->num=r; printf("%d ",r); break; } else { // // } } }

// } // } sum[i]= countTSP(i); father[i]->sum=sum[i]; printf("%lf \n",sum[i]); showinfor(); minTSP(father[0]->general); minall=min; allbest=fatherbest; allbest->general=fatherbest->general; allbest->sum=minall; for(int j=0;jcity[j]=fatherbest->city[j]; //生成一个随机数，看是否能产生变异 if(variance>=(double)rand() / ((double)RAND_MAX + 1) * 10) { printf("Can variance \n"); fprintf(result,"Can variance \n"); variant(); } //交叉 //选择群体中部分优秀的个体 choice(); printf("Cross begining...\n"); fprintf(result,"Cross begining...\n"); crossGA(); } double countTSP(int index) { double a=0,x1,y1,tmp; for(int i=0;icity[i]->x-father[index]->city[i+1]->x; y1=father[index]->city[i]->y-father[index]->city[i+1]->y; tmp=sqrt(x1*x1+y1*y1); a=a+tmp; x1=father[index]->city[0]->x-father[index]->city[n-1]->x; y1=father[index]->city[0]->y-father[index]->city[n-1]->y; }

tmp=sqrt(x1*x1+y1*y1); a=a+tmp; return a; } void minTSP(int gen) { int a; min=sum[0]; for(int i=0;i<30;i++) { if(min>=sum[i] && sum[i]!=0) { min=sum[i]; a=i; } } // fatherbest=father[a]; fatherbest->general=gen; fatherbest->sum=min; //保存种群中最优的一条路径 for(int jj=0;jjcity[jj]=father[a]->city[jj]; printf("当代最优个体编号为： %d \n",a+1); fprintf(result,"当代最优个体编号为： %d \n",a+1); printf("最短路程是： %lf \n",sum[a]); fprintf(result,"最短路程是： %lf \n",sum[a]); printf("这是第 %d 代的最短路程: \n",gen); fprintf(result,"这是第 %d 代的最短路程: \n",gen); for(int j=0;jcity[j]->num); ",fatherbest->city[j]->num); } printf("\n"); fprintf(result,"\n"); } void variant() { //变异过程为随机变异 n 条每条交换任意两个节点的位置

分享到：

赞收藏

资料库

遗传算法求解10城市的旅行商问题的c语言.doc

相关推荐

课程资源

热门标签

最新资料