第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
北航数值分析第一题解题分析报告.doc
北航数值分析作业第一题：
北航数值分析作业第一题：
一、算法设计方案
1. 要求计算矩阵的最大最小特征值，通过幂法求得模最大的特征值，进行一定
判断即得所求结果；
2. 求解与给定数值接近的特征值，可以该数做漂移量，新数组特征值倒数的绝
对值满足反幂法的要求，故通过反幂法即可求得；
3. 反幂法计算时需要方程求解中间过渡向量，需设计 Doolite 分解求解；
4.
|A|=|B||C|，故要求解矩阵的秩，只需将 Doolite 分解后的 U 矩阵的对角线相
乘即为矩阵的 Det。
算法编译环境：vlsual c++6.0
需要编译函数：幂法，反幂法，Doolite 分解及方程的求解
二、源程序如下：
#include
#include
#include
#include
int Max(int value1,int value2);
int Min(int value1,int value2);
void Transform(double A[5][501]);
double mifa(double A[5][501]);
void daizhuangdoolite(double A[5][501],double x[501],double b[501]);
double fanmifa(double A[5][501]);
double Det(double A[5][501]);
/***定义 2 个判断大小的函数，便于以后调用***/
int Max(int value1,int value2)
{
return((value1>value2)?value1:value2);
}
int Min(int value1,int value2)
{
return ((value1
/***将矩阵值转存在一个数组里，节省空间***/
void Transform(double A[5][501],double b,double c)
{
int i=0,j=0;
A[i][j]=0,A[i][j+1]=0;
for(j=2;j<=500;j++)
A[i][j]=c;
i++;
j=0;
A[i][j]=0;
for(j=1;j<=500;j++)
A[i][j]=b;
i++;
for(j=0;j<=500;j++)
A[i][j]=(1.64-0.024*(j+1))*sin(0.2*(j+1))-0.64*exp(0.1/(j+1));
i++;
for(j=0;j<=499;j++)
A[i][j]=b;
A[i][j]=0;
i++;
for(j=0;j<=498;j++)
A[i][j]=c;
A[i][j]=0,A[i][j+1]=0;
}
/***转存结束***/
//用于求解模最大的特征值，幂法
double mifa(double A[5][501])
{
int s=2,r=2,m=0,i,j;
double b2,b1=0,sum,u[501],y[501];
for (i=0;i<=500;i++)
{
u[i] = 1.0;
}
do
{
sum=0;
if(m!=0)b1=b2;
m++;
for(i=0;i<=500;i++)
sum+=u[i]*u[i];
for(i=0;i<=500;i++)
y[i]=u[i]/sqrt(sum);
for(i=0;i<=500;i++)
{
u[i]=0;
for(j=Max(i-r,0);j<=Min(i+s,500);j++)
u[i]=u[i]+A[i-j+s][j]*y[j];
}
b2=0;
for(i=0;i<=500;i++)
b2=b2+y[i]*u[i];
}
while(fabs(b2-b1)/fabs(b2)>=exp(-12));
return b2;
}
//带状 DOOLITE 分解，并且求解出方程组的解
void daizhuangdoolite(double A[5][501],double x[501],double b[501])
{
int i,j,k,t,s=2,r=2;
double B[5][501],c[501];
for(i=0;i<=4;i++)
{
for(j=0;j<=500;j++)
B[i][j]=A[i][j];
}
for(i=0;i<=500;i++)
c[i]=b[i];
for(k=0;k<=500;k++)
{
for(j=k;j<=Min(k+s,500);j++)
{
for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)
B[k-j+s][j]=B[k-j+s][j]-B[k-t+s][t]*B[t-j+s][j];
}
for(i=k+1;i<=Min(k+r,500);i++)
{
for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)
B[i-k+s][k]=B[i-k+s][k]-B[i-t+s][t]*B[t-k+s][k];
B[i-k+s][k]=B[i-k+s][k]/B[s][k];
}
}
for(i=1;i<=500;i++)
for(t=Max(0,i-r);t<=i-1;t++)
c[i]=c[i]-B[i-t+s][t]*c[t];
x[500]=c[500]/B[s][500];
for(i=499;i>=0;i--)
{
x[i]=c[i];
for(t=i+1;t<=Min(i+s,500);t++)
x[i]=x[i]-B[i-t+s][t]*x[t];
x[i]=x[i]/B[s][i];
}
}
//用于求解模最大的特征值，反幂法
double fanmifa(double A[5][501])
{
int s=2,r=2,m=0,i;
double b2,b1=0,sum=0,u[501],y[501];
for (i=0;i<=500;i++)
{
u[i] = 1.0;
}
while(fabs(b2-b1)>=fabs(b1)*exp(-12));
return 1/b2;
}
//行列式的 LU 分解，U 的主线乘积即位矩阵的 DET
double Det(double A[5][501])
{
int i,j,k,t,s=2,r=2;
for(k=0;k<=500;k++)
{
}
do
{
if(m!=0)b1=b2;
m++;
sum=0;
for(i=0;i<=500;i++)
sum+=u[i]*u[i];
for(i=0;i<=500;i++)
y[i]=u[i]/sqrt(sum);
daizhuangdoolite(A,u,y);
b2=0;
for(i=0;i<=500;i++)
b2+=y[i]*u[i];
}
}
double det=1;
for(i=0;i<=500;i++)
det*=A[s][i];
return det;
}
void main()
{
double b=0.16,c=-0.064,p,q;
int i,j;
double A[5][501];
Transform(A,b,c); //进行 A 的赋值
cout.precision(12); //定义输出精度
double lamda1,lamda501,lamdas;
double k=mifa(A);
if(k>0)
值值，
for(j=k;j<=Min(k+s,500);j++)
{
for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)
A[k-j+s][j]=A[k-j+s][j]-A[k-t+s][t]*A[t-j+s][j];
}
for(i=k+1;i<=Min(k+r,500);i++)
{
for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)
A[i-k+s][k]=A[i-k+s][k]-A[i-t+s][t]*A[t-k+s][k];
A[i-k+s][k]=A[i-k+s][k]/A[s][k];
//判断求得最大以及最小的特征值.如果 K>0，则它为最大特征
{
//并以它为偏移量再用一次幂法求得新矩阵最大特征值，即为最大
//与最小的特征值的差
lamda501=k;
for(i=0;i<=500;i++)
A[2][i]=A[2][i]-k;
lamda1=mifa(A)+lamda501;
for(i=0;i<=500;i++)
A[2][i]=A[2][i]+k;
}
else
幂法
{
//如果 K<=0，则它为最小特征值值，并以它为偏移量再用一次
//求得新矩阵最大特征值，即为最大与最小的特征值的差
}
lamdas=fanmifa(A);
FILE *fp=fopen("result.txt","w");
fprintf(fp,"λ1=%.12e\n",lamda1);
fprintf(fp,"λ501=%.12e\n",lamda501);
fprintf(fp,"λs=%.12e\n\n",lamdas);
fprintf(fp,"\t 要求接近的值\t\t\t 实际求得的特征值\n");
for(i=1;i<=39;i++)
{
//反幂法求得与给定值接近的特征值
p=lamda1+(i+1)*(lamda501-lamda1)/40;
for(j=0;j<=500;j++)
A[2][j]=A[2][j]-p;
q=fanmifa(A)+p;
for(j=0;j<=500;j++)
A[2][j]=A[2][j]+p;
fprintf(fp,"μ%d: %.12e
λi%d: %.12e\n",i,p,i,q);
lamda1=k;
for(i=0;i<=500;i++)
A[2][i]=A[2][i]-k;
lamda501=mifa(A)+lamda1;
for(i=0;i<=500;i++)
A[2][i]=A[2][i]+k;
}
double cond=fabs(mifa(A)/fanmifa(A));
double det=Det(A);
fprintf(fp,"\ncond(A)=%.12e\n",cond);
fprintf(fp,"\ndetA=%.12e\n",det);
}
三、程序运行结果
λ1=-1.069936345952e+001
λ501=9.722283648681e+000
λs=-5.557989086521e-003
要求接近的值
实际求得的特征值
μ1: -9.678281104107e+000
μ2: -9.167739926402e+000
μ3: -8.657198748697e+000
μ4: -8.146657570993e+000
μ5: -7.636116393288e+000
μ6: -7.125575215583e+000
μ7: -6.615034037878e+000
μ8: -6.104492860173e+000
μ9: -5.593951682468e+000
λi1: -9.585702058251e+000
λi2: -9.172672423948e+000
λi3: -8.652284007885e+000
λi4: -8.093482780052e+000
λi5: -7.659405420574e+000
λi6: -7.119684646576e+000
λi7: -6.611764337314e+000
λi8: -6.066103126985e+000
λi9: -5.585101045269e+000
μ10: -5.083410504763e+000
μ11: -4.572869327058e+000
μ12: -4.062328149353e+000
μ13: -3.551786971648e+000
μ14: -3.041245793943e+000
μ15: -2.530704616238e+000
μ16: -2.020163438533e+000
μ17: -1.509622260828e+000
μ18: -9.990810831232e-001
μ19: -4.885399054182e-001
μ20: 2.200127228676e-002
μ21: 5.325424499917e-001
μ22: 1.043083627697e+000
μ23: 1.553624805402e+000
μ24: 2.064165983107e+000
μ25: 2.574707160812e+000
μ26: 3.085248338516e+000
μ27: 3.595789516221e+000
μ28: 4.106330693926e+000
μ29: 4.616871871631e+000
μ30: 5.127413049336e+000
μ31: 5.637954227041e+000
μ32: 6.148495404746e+000
μ33: 6.659036582451e+000
μ34: 7.169577760156e+000
μ35: 7.680118937861e+000
μ36: 8.190660115566e+000
μ37: 8.701201293271e+000
μ38: 9.211742470976e+000
μ39: 9.722283648681e+000
cond(A)=1.925042185755e+003
detA=2.772786141752e+118
四、分析
λi10: -5.114083539196e+000
λi11: -4.578872177367e+000
λi12: -4.096473385708e+000
λi13: -3.554211216942e+000
λi14: -3.041090018133e+000
λi15: -2.533970334136e+000
λi16: -2.003230401311e+000
λi17: -1.503557606947e+000
λi18: -9.935585987809e-001
λi19: -4.870426734583e-001
λi20: 2.231736249587e-002
λi21: 5.324174742068e-001
λi22: 1.052898964020e+000
λi23: 1.589445977158e+000
λi24: 2.060330427561e+000
λi25: 2.558075576223e+000
λi26: 3.080240508465e+000
λi27: 3.613620874136e+000
λi28: 4.091378506834e+000
λi29: 4.603035354280e+000
λi30: 5.132924284378e+000
λi31: 5.594906275501e+000
λi32: 6.080933498348e+000
λi33: 6.680354121496e+000
λi34: 7.293878467852e+000
λi35: 7.717111851857e+000
λi36: 8.225220016407e+000
λi37: 8.648665837870e+000
λi38: 9.254200347303e+000
λi39: 9.724634099672e+000
如果初始向量选择不当,将导致迭代中 X1 的系数等于零.但是，由于舍入误
差的影响,经若干步迭代后,.按照基向量展开时,x1 的系数可能不等于零。把这一
向量看作初始向量，用幂法继续求向量序列,仍然会得出预期的结果,不过收敛速
度较慢.如果收敛很慢,可改换初始向量,所以初始向量的选取会影响到迭代的次
数。
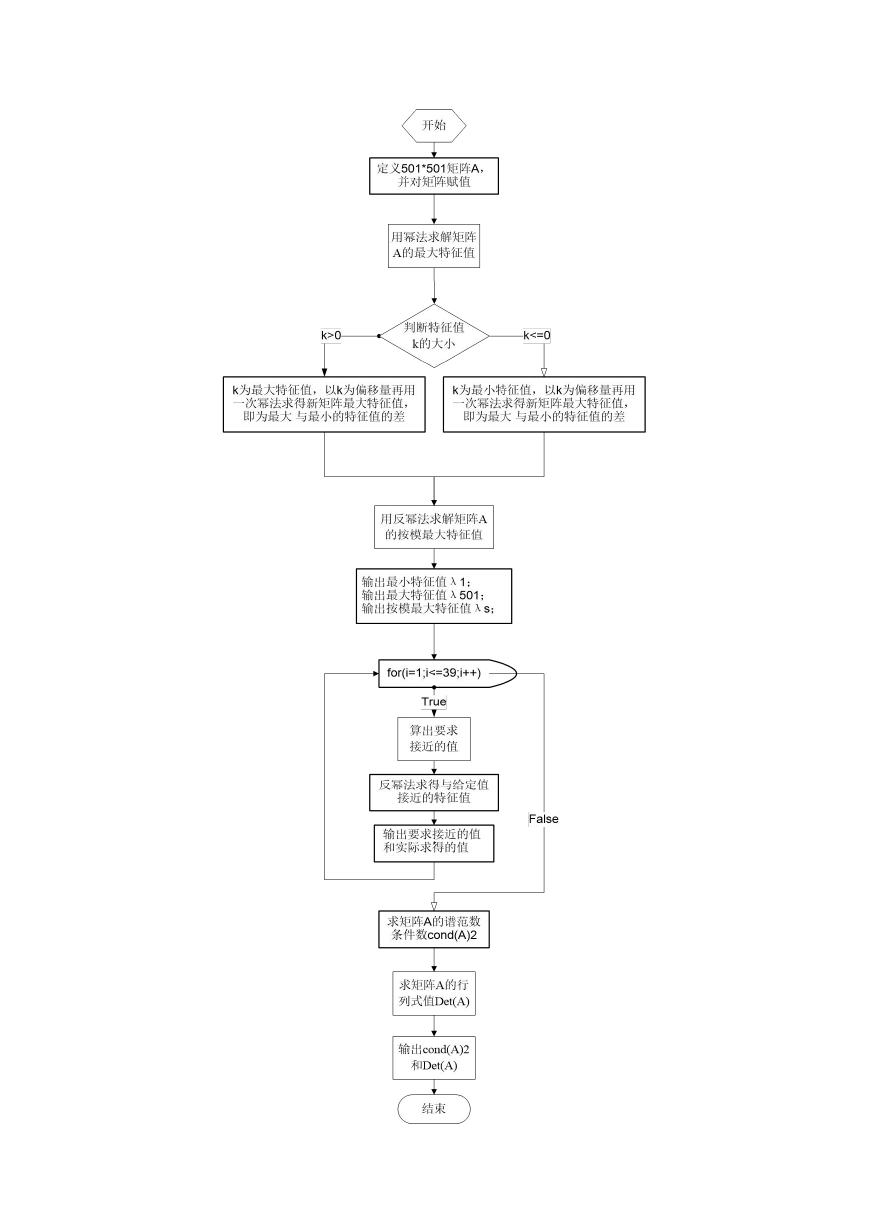
五、流程图
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
