中国科技论文在线 http://www.paper.edu.cn 基于 LINGO 的机组组合优化 陈雁飞1，周继鹏2* （1. 华侨大学电子系，厦门 361021； 2. 华侨大学化工与制药工程系，厦门 361021） 摘要：为了研究机组组合的情况，本文以机组总费用最小为目标，以机组的物理特性以及电 力系统的限制为约束条件，应用数学规划的方法建立了一个关于机组组合的简单数学优化模 型。我们采用一种简单的 IEEE 3 节点电力系统进行测试，运用建立的数学优化模型并且通 过 LINGO 软件求解得出了 3 母线系统在 4 小时内的最优组合计划和总费用大小。这种优化 建模求解机组组合的方法简单、方便，所建立的数学优化模型可以推广到其它复杂的电力系 统，模型具有一定的可推广性。 关键词： 机组组合；优化设计；LINGO 软件 中图分类号：TM715 The Unit Commitment Based on LINGO CHEN Yanfei1, ZHOU Jipeng2 (1. Electronic engineering,HUAQIAO University,Xia men 361021; 2. Chemcial and pharmaceutiacl engineering,HUAQIAO University,Xia men 361021) Abstract: In order to study the situation of unit commitment, this paper is based on the target of minimizing total cost of unit and establish constraint conditions in the limit of physical unit and power system.However, we establish a simple maths modeling about the unit commitment through by the method of mathematical programming.Then,we use a simple power system of IEEE 3 node to test the math modeling.What's more,we use the LINGO software to solve the modeling and get the optimal combination plan and total cost based on 3 Buses within 4 hours.This solving method which is optimization modeling is simple and convenient.At last, we also can use the modeling in the others complex power systems.So the modeling has a certain promotion. Key words: unit commitmtent; optimal design; LINGO software 0 引言 当前的科学技术还不能有效地存储电力，所以电力生产和消费在任何时刻都要相等，否 则就会威胁电力系统安全运行。又由于发电机组的物理特性限制，发电机组不能够随心所欲 地发出需要的电力。为了能够实时平衡变化剧烈的电力负荷，电力部门往往需要根据预测的 未来电力负荷安排发电机组起停计划，在满足电力系统安全运行条件下，追求发电成本最小。 机组组合问题是一个混合整数规划问题，目前，人们起初的求解该问题的算法有很多， 如：拉格朗日松弛法[1]、遗传算法[2]、模式搜索算法[3]、集结投影次梯度算法[4]等。但是这 些算法编程复杂，不容易理解。随着 LINGO 软件的不断发展，为求解该类优化问题提供了 一种相对简单的方法。 1 基本假设和符号说明 1.1 基本假设 （1） 假设机组成本由启动成本、空载成本和增量成本三个部分组成； （2） 假设机组在运行过程中不会发生任何故障； 作者简介：陈雁飞（1989—），男，华侨大学在读本科生，主要研究方向：电子信息. E-mail: 450822486@qq.com - 1 - 

中国科技论文在线 http://www.paper.edu.cn （3） 假设机组的运行是以小时为单位； （4） 假设机组的启动成本、空载成本保持不变； （5） 假设机组的发电量和负载的负荷在任一小时内不会发生变化； 1.2 符号说明 i : 机组的台数， i=1,2,…,n； j : 机组计划运行的时间,j=1,2,…,m； ,i ja : 第 i 台机组第 j 小时初的运行状态，“1”表示启动，“0”表示未启动； ,i jC : 第 i 台机组第 j 小时内的出力；（单位：MW） jL : 电力系统在第 j 小时的负荷电量；（单位：MW） jB : 电力系统在第 j 小时的电力备用要求；（单位：MW） ,i jx : 第 i 台机组第 j 小时的运行状态，“1”表示运行，“0”表示停运； 这里给出主要符号的说明，其它符号将在文章中给出，这里不再赘述。 2 模型建立 2.1 目标函数的确立 令 F 表示机组运行的总成本大小，则 F 由启动成本、运行成本和增量成本三部分组成。 根据假设 4，令第 i 台机组的启动成本与空载成本分别表示 iQ 和 iK ，由于增量成本的计算 比较复杂，这里仅以 iZ 表示，在问题中具体计算。因此，目标函数为 min F = n m ∑ ∑ ( j 1 = ⎡ ⎢ ⎣ i 1 = ( Q a i i j , + K x i i j , )) + Z i (1) ⎤ ⎥ ⎦ 2.2 约束条件的确立 j L C i j , (2) （1）负荷平衡约束，在任一小时内机组总的出力应该等于电力系统的负荷，即 n =∑ i 1 = （2）系统备用约束要求，任一小时，机组的备用电量必须大于系统的备用要求，即 n ∑ MAX C x ) i j , (3) B − > ( i j i , j i 1 = 其中 iMAX 表示第 i 台机组的最大出力。 （3）输电线传输容量约束，在任一小时内，输电线传输的电能必须在它的最大传输能 力范围内。这里，我们定义一个算子⊗ ,它代表两个矩阵之间的运算，前一矩阵的每行元素 k lE k 与后一矩阵的对应行相乘后取和式。 , ( 表示传输线路数， 表示节点的个数 表示线 性转移系数矩阵， ,j lP 表示第l 个节点在第 j 小时的注入功率，那么二者相互运算后会产生 一个 k 行 j 列矩阵，表示每条线路在 j 小时的传输的电能，约束条件可以写为： ) l d ⊗ | ≤ P j l , E | k l , kd 表示第 k 条输电线的最大电能传输能力。 (4) k - 2 - 

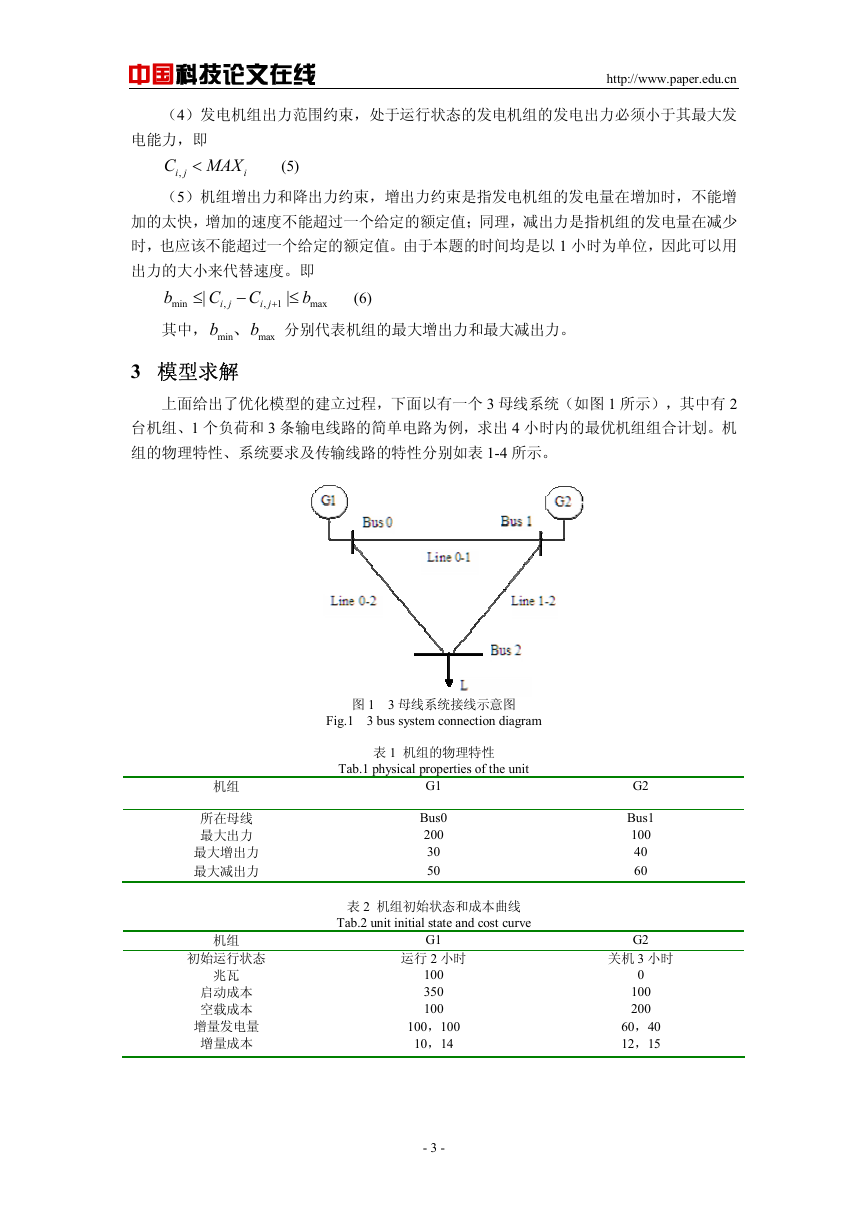
中国科技论文在线 http://www.paper.edu.cn （4）发电机组出力范围约束，处于运行状态的发电机组的发电出力必须小于其最大发 电能力，即 < i MAX (5) C ,i j （5）机组增出力和降出力约束，增出力约束是指发电机组的发电量在增加时，不能增 加的太快，增加的速度不能超过一个给定的额定值；同理，减出力是指机组的发电量在减少 时，也应该不能超过一个给定的额定值。由于本题的时间均是以 1 小时为单位，因此可以用 出力的大小来代替速度。即 b max b min | ≤ | ≤ C i j , b C i j , 1 + − b、 分别代表机组的最大增出力和最大减出力。 (6) max 其中， min 3 模型求解 上面给出了优化模型的建立过程，下面以有一个 3 母线系统（如图 1 所示），其中有 2 台机组、1 个负荷和 3 条输电线路的简单电路为例，求出 4 小时内的最优机组组合计划。机 组的物理特性、系统要求及传输线路的特性分别如表 1-4 所示。 机组 所在母线 最大出力 最大增出力 最大减出力 机组 初始运行状态 兆瓦 启动成本 空载成本 增量发电量 增量成本 G2 Bus1 100 40 60 G2 关机 3 小时 0 100 200 60，40 12，15 图 1 3 母线系统接线示意图 Fig.1 3 bus system connection diagram 表 1 机组的物理特性 Tab.1 physical properties of the unit 表 2 机组初始状态和成本曲线 Tab.2 unit initial state and cost curve G1 Bus0 200 30 50 G1 运行 2 小时 100 350 100 100，100 10，14 - 3 - 

中国科技论文在线 http://www.paper.edu.cn 表 3 系统负荷和备用 Tab.3 system load and set aside 小时 负荷 系统备用 1 100 20 2 130 30 3 120 50 4 140 40 表 4 线性转移系数及最大传输容量 Tab.4 linear transfer factor and the max transmission capacity Bus0 转移系数 Bus2 转移系数 Bus1 转移系数 线路 line0-1 Line0-2 Line1-2 根据上面的分析，结合题目给出的数据，我们可以确定优化模型及其约束条件。 首先计算机组的增量成本 Zi （i=1,2），为了计算的方便，这里我们引入 ,i jb ，它的含 -0.3333 -0.6777 -0.3333 -0.6667 -0.3333 0.3333 200 100 200 传输容量 0 0 0 义如下所示， ∈ 0, 因此，我们可以写出增量成本 1, ⎧ ⎨ ⎩ C 1, b 1, = j j [100,200] 其它 , b 2, j = 1, ⎧ ⎨ ⎩ C 2, [60,100] ∈ j 0, 其它 4 ∑ j 1 = C (10 1, j + C 12 2, j + 4( C 1, j − b 100) 1, j + 3( C 2, j − b 60) 2, j ) 其次，还要确定机组的初始状态， x 1,0 x 2,0 ⎧ ⎨ ⎩ C 1, = 1,0 C 0, = = 100 0 = 2,0 综上所述，得出优化模型[5]为 (i=1,2;j=1,2,3,4) ： (7) (8) (9) min 4 ∑ j 1 = 350 a 1, j + 100 a 2, j + 100 x 1, j + 200 x 2, j + C 10 1, j + C 12 2, j + 4( C 1, j − b 100) 1, j + 3( C 2, j − 60) b 2, j ⎡ ⎣ ⎤ ⎦ (10) 2 i j j (12) j 2, 2, j L C i j , (11) S.T. (13) H ≥ j j 200 ≤ 100 ≤ 200 =∑ 1 = C x C x (100 (200 ) ) + − − j j 1, 1 2, C L 0.6667 200 0.3333 + − ≤ − L C 100 0.3333 0.6667 − + ≤ − j j 2, L C 200 0.3333 0.3333 + − ≤ ≤ j j 2, C C 200,0 0 100 ≤ ≤ (14) j j 1, 2, C C | 50 30 | − ≤ ≤ 1, 1, C C 40 | | 60 ≤ ≤ − j j 2, 1 2, + x x C 0 1, 100, 0, = (16) = = = 1,0 1,0 2,0 C 1, [100,200] 1, ∈ ⎧ ⎧ i j , ⎨ ⎨ 0, 其它 ⎩ ⎩ x 1, 1 = ⎧ i j , = ⎨ 0, ⎩ 其它情况 (15) {0,1}, + − 1 C 2, a i j , x i j , x i j , b 2, b 1, C ∈ < < = = j j 1 + 2,0 , j j [60,100] ∈ j 0, 其它 (17) (18) - 4 - 

中国科技论文在线 http://www.paper.edu.cn 根据以上模型运用 LINGO11.0 编程[6]求解得出结果如表 5 所示： 机组 G1 G2 1 1 0 表 5 最优组合计划表 Tab.5 the optimal combination frame 各小时运行状态 2 1 1 3 1 1 4 1 0 1 100 0 各小时出力/MW 2 100 30 3 110 60 成本/元 6680 4 140 0 从上表中可以看出，机组 G1 在 4 小时内一直处于运行状态，机组 G2 在第 2、3 小时处 于运行状态，此时的成本费用为 6680 元。 4 结论 本文从最优化的角度入手，分析了总成本最小的目标函数以及约束方程，建立了机组组 合的优化方程，最后用简单的 3 母线系统进行测试，并且运用 LINGO 软件进行求解，方便 简洁，适合工程应用。对于其它复杂的母线系统，该优化模型也是适用的，模型具有一定的 通用性。 [参考文献] (References) [1] 潘常春，杨根科，孙凯，等（etal）.待最小批量约束的计划问题及其拉格朗日松弛算法[J].控制理论与应 用，2009，26（2）：133~138. [2] 张立勇，张焰，蒋佳文. 基于矩阵实数编码遗传算法求解大规模机组组合问题[J].中国电机工程学报， 2006，26（2）：82~87. [3] 黎静华，韦华. 基于模式搜索算法的电力系统机组组合问题[J].电工技术学报，2009，24（6）：121~128. [4] 苗青，曹广益，朱新坚.基于集结投影次梯度的机组组合算法研究[J].计算机仿真，2008，25（12）：245~247. [5] 姜启源，谢金星，叶俊.数学模型（第三版）[M]. 北京：高等教育出版社，2003. [6] 谢金星，薛毅编著. 优化建模与 LINDO/LINGO 软件[M].北京：清华大学出版社，2005. - 5 -