logo资料库

SAT-DPLL——Optimized.docx

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：1.70M 资料格式：docx 举报 版权申诉
第1页 / 共55页
第2页 / 共55页
第3页 / 共55页
第4页 / 共55页
第5页 / 共55页
第6页 / 共55页
第7页 / 共55页
第8页 / 共55页
资料共55页，剩余部分请下载后查看
    任 务 书
    1 引言
    1.1 课题背景与意义
    1.1.1 课题研究背景
    1.1.2 SAT问题研究意义
    1.2 可满足性问题的研究现状及挑战
    1.3课程设计的主要研究工作
    2 系统需求分析与总体设计
    2.1 系统需求分析
    2.2 系统总体设计
    2.2.1 系统总流程
    2.2.2 模块功能描述
    3 系统详细设计
    3.1 数据结构定义
    3.2 主要算法设计
    3.2.1 CnfParser模块
    3.2.2 DPLLSolver模块
    3.2.3 Sudoku模块
    3.2.4 DPLL的优化算法
    4 系统实现与测试
    4.1 系统实现
    4.2 系统测试
    4.2.1 常用测试方法：
    4.2.2 DPLL测试
    4.2.3 数独测试
    5总结与展望
    5.1 全文总结
    5.2 工作展望
    6 体 会
    参考文献
    附录 1 算法实现
    Global.h
    Main.cpp
    Start.cpp
    CnfPaser.cpp
    DPLLSolver.cpp
    Sudoku.cpp
    附录2 优化后的DPLL算法
    课程设计报告 题目： 基于 SAT 的数独游戏求解程序 课程名称： 综合程序设计课程设计 专业班级： 学 号： 姓 名： 指导教师： 报告日期： 信息安全 1701 U201714868 罗南清 李剑军 2019-02-28 计算机科学与技术学院 I
    任 务 书 1.题目名称：基于 SAT 的数独游戏求解程序 2.设计内容 SAT 问题即命题逻辑公式的可满足性问题（satisfiability problem），是计算 机科学与人工智能基本问题，是一个典型的 NP 完全问题，可广泛应用于许多实 际问题如硬件设计、安全协议验证等，具有重要理论意义与应用价值。本设计要 求基于 DPLL 算法实现一个完备 SAT 求解器，对输入的 CNF 范式算例文件，解 析并建立其内部表示；精心设计问题中变元、文字、子句、公式等有效的物理存 储结构以及一定的分支变元处理策略，使求解器具有优化的执行性能；对一定规 模的算例能有效求解，输出与文件保存求解结果，统计求解时间。 3.设计要求 要求具有如下功能： 1）输入输出功能：包括程序执行参数的输入，SAT 算例 cnf 文件的读取， 执行结果的输出与文件保存等。(15%) 2）公式解析与验证：读取 cnf 算例文件，解析文件，基于一定的物理结构， 建立公式的内部表示；并实现对解析正确性的验证功能，即遍历内部结构逐行输 出与显示每个子句，与输入算例对比可人工判断解析功能的正确性。数据结构的 设计可参考文献[1-3]。(15%) 3）DPLL 过程：基于 DPLL 算法框架，实现 SAT 算例的求解。(35%) 4）时间性能的测量：基于相应的时间处理函数（参考 time.h），记录 DPLL 过程执行时间（以毫秒为单位），并作为输出信息的一部分。(5%) 5）程序优化：对基本 DPLL 的实现进行存储结构、分支变元选取策略[1-3] 等某一方面进行优化设计与实现，提供较明确的性能优化率结果。优化率的计算 公式为：[(t-to)/t]*100%,其中 t 为未对 DPLL 优化时求解基准算例的执行时间，to 则为优化 DPLL 实现时求解同一算例的执行时间。(15%) 6）SAT 应用：将数独游戏[5]问题转化为 SAT 问题[6-8]，并集成到上面的求 解器进行问题求解，游戏可玩，具有一定的/简单的交互性。应用问题归约为 SAT I
    问题的具体方法可参考文献[3]与[6-8]。(15%) 4.参考文献 [1] 张健著. 逻辑公式的可满足性判定—方法、工具及应用. 科学出版社， 2000 [2]Tanbir Ahmed. An Implementation of the DPLL Algorithm. Master thesis, Concordia University,Canada,2009 [3] 陈稳. 基于 DPLL 的 SAT 算法的研究与应用.硕士学位论文，电子科技大 学，2011 [4]Carsten Sinz.Visualizing SAT Instances and Runs of the DPLL Algorithm.J Autom Reasoning (2007) 39:219–243 [5] 360 百科：数独游戏 https://baike.so.com/doc/3390505-3569059.html [6] Tjark Weber. A sat-based sudoku solver. In 12th International Conference on Logic forProgramming, Artificial Intelligence and Reasoning, LPAR 2005, pages 11–15, 2005. [7]Ins Lynce and Jol Ouaknine. Sudoku as a sat problem.In Proceedings of the 9th InternationalSymposium on Artificial Intelligence and Mathematics, AIMATH 2006, Fort Lauderdale.Springer,2006. [8] Uwe Pfeiffer, Tomas Karnagel and Guido Scheffler. A Sudoku-Solver for Large Puzzles using SAT. LPAR-17-short (EPiC Series, vol. 13), 52–57 [9] Sudoku Puzzles Generating: from Easy to Evil. http://zhangroup.aporc.org/images/files/Paper_3485.pdf [10] Robert Ganian and Stefan Szeider. Community Structure Inspired Algorithms for SAT and #SAT. International Conference on Theory and Applications of Satisfiability Testing(SAT 2015),223-237360 II
    目 录 任 务 书 ....................................................... I 1 引言 ......................................................... 1 1.1 课题背景与意义 ......................................... 1 1.2 可满足性问题的研究现状及挑战 ........................... 2 1.3 课程设计的主要研究工作 ................................. 3 2 系统需求分析与总体设计 ....................................... 4 2.1 系统需求分析 ........................................... 4 2.2 系统总体设计 ........................................... 4 3 系统详细设计 ................................................. 7 3.1 数据结构定义 ........................................... 7 3.2 主要算法设计 ........................................... 8 4 系统实现与测试 .............................................. 15 4.1 系统实现 .............................................. 15 4.2 系统测试 .............................................. 16 5 总结与展望 ................................................. 26 5.1 全文总结 .............................................. 26 5.2 工作展望 .............................................. 27 6 体会 ....................................................... 28 参考文献 ...................................................... 29 附录 1 算法实现 ............................................... 30 附录 2 优化后的 DPLL 算法 ...................................... 45 III
    1 引言 1.1 课题背景与意义 1.1.1 课题研究背景 SAT 问题是对一个以合取范式（conjunctive Normal Form，简称 CNF）的形 势给出的命题逻辑公式进行判断，以找出是否存在一个真值指派，是的该命题逻 辑为真。 从上世纪 60 年代至今，世界各国研究人员对 SAT 问题做了大量工作，对于 解决 SAT 问题提出了许多可行有效的方案。SAT 问题已经成为计算机领域和人 工智能领域所要研究的中心问题，被称为理论计算机和数理逻辑的第一问题，在 硬件验证、人工智能、电子设计自动化、自动化推理、组合等式检测等领域具有 飞车那个重要的理论和实践意义。 每年可满足理论和应用方面的额国际会议都会组织一次 SAT 竞赛以求找到 一组最快的 SAT 求解器，而且会详细展示求解器的性能。尽管命题逻辑的可满 足性问题理论研究已经趋于成熟，但在 SAT 求解器被越来越多应用到各种实际 问题领域的今天，探寻解决 SAT 问题的高效算法仍然是一个吸引人并且几句挑 战性的研究方向。 1.1.2 SAT 问题研究意义 可满足性问题时计算机科学领域和人工智能等领域中的重要研究对象。对于 一个含有 n 个命题逻辑变量的合取范式来说，若采用穷举法来罗列所有真值指派 进行求解，虽然在理论上是可行的，但算法的时间复杂度却是指数级规模，为 O(2n),计算机如果采用这种方式将负担不起巨大的开销，搜索空间如此庞大，是 的计算机无法在可等待的时间得出解，产生组合爆炸问题。 布尔表达式的可满足性问题属于 NP 完全问题，现实生活中存在大量的 NP 完全问题，寻找高效快速的算法来解决该类问题是计算机理论研究和实际应用中 的重要工作。如果找到解决 SAT 问题的有效路径，那么一定可以高效的解决所有 其他 NP 完全问题，所以设计和实现更高效的求解算法意义重大。 1
    SAT 问题应用领域非常广泛，例如在数学研究和应用领域，它能用来解决旅 行商（Traveling Salesman Problem, TSP）和逻辑算术问题：在计算机和人工 智能（Artificial Intelligence，AI）领域中，它能解决 CSP（约束满足问题） 问题、语义信息的处理和逻辑编程等问题；在计算机辅助设计领域中，它能很好 的解决任务规划与设计、三维物体识别等问题。 许多实际问题如人工智能、积木世界规划问题、数据库检索、Job shop 排 工问题、超大规模集成电路设计和图着色都可转换成 SAT 问题进行求解。 1.2 可满足性问题的研究现状及挑战 SAT 算法主要归结为两大类：完备算法（也称回溯搜索算法）和局部搜索 算法。其中，完备算法大都是基于回溯搜索的，局部搜索算法是基于局部随机搜 索的。完备算法基于穷举法思想，它的优点是能保证找到对应 SAT 问题或证明 公式不可满足，但是效率极低，它的平均时间复杂度是多项式级的，但是最坏情 况下的时间复杂度却是指数级的。一些完备算法采用了精巧的技术减小搜索空间 和问题规模，提高了算法的时间效率。局部搜索算法相对于完备算法而言，由于 采用了启发式策略来指导搜索，是的求解速度相对较快，但是在某些实例上可能 得不到解，他不保证一定能够找到对应 SAT 问题的解，即它不饿能证明 SAT 问 题的不可满足性。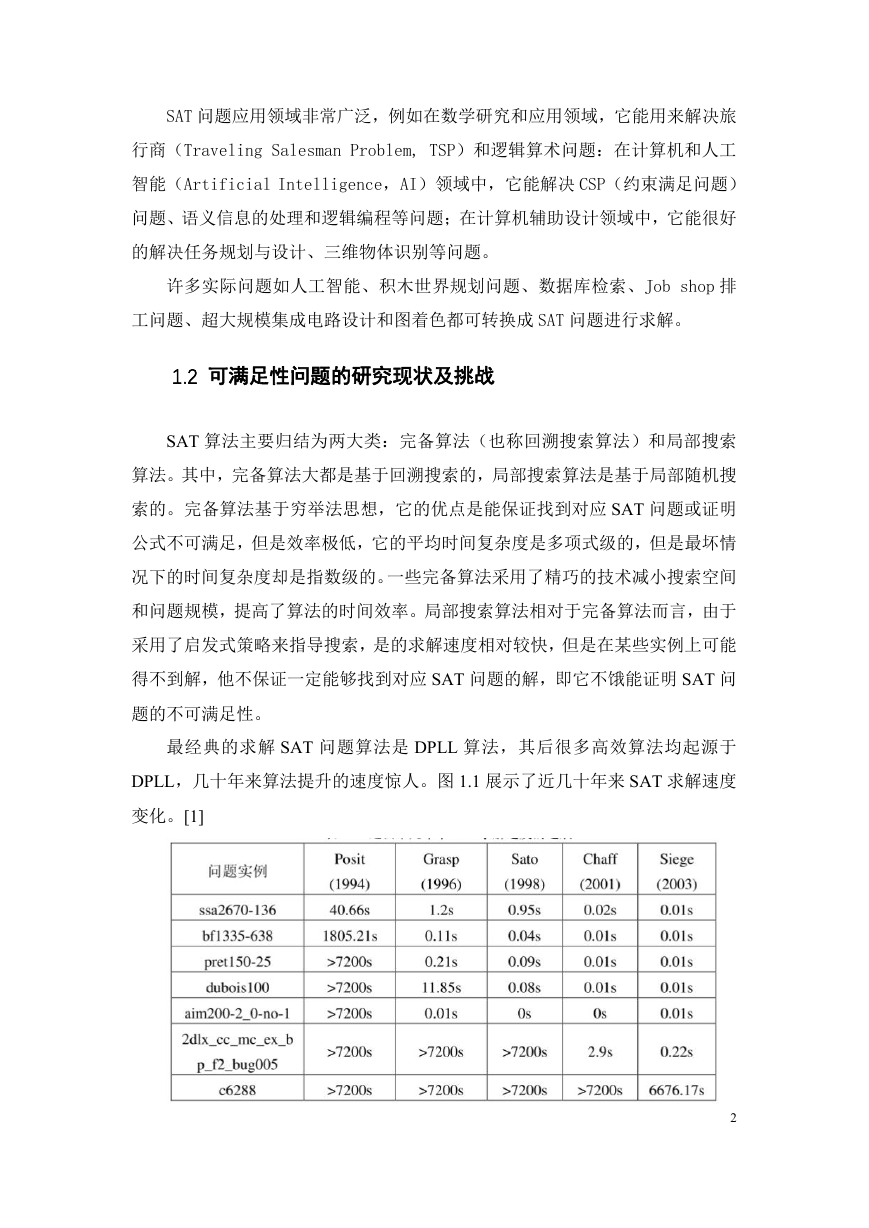 最经典的求解 SAT 问题算法是 DPLL 算法，其后很多高效算法均起源于 DPLL，几十年来算法提升的速度惊人。图 1.1 展示了近几十年来 SAT 求解速度 变化。[1] 2
    图 1.1 过去十几年 SAT 求解器速度的进展 尽管 SAT 算法已经取得了很大的改进，但是仍然有些问题没有得到高效的 解决，已经解决的问题可能还存在更好的求解算法，因此实现更高效率的算法仍 然是当前要解决的中心问题之一。 1.3 课程设计的主要研究工作 本课程设计的主要研究工作如下： （1）对 SAT 问题的研究背景、意义及现状进行了简要总结，学习了命题逻 辑可满足性问题的基本理论知识。 （2）对 DPLL 算法进行了代码实现，并使用多组 CNF 案例进行检测，得出 最后结论。 （3）对 DPLL 算法进行优化，本课程设计着重对 DPLL 中变元的选择策略 进行了优化。 （4）创建数独问题并利用挖洞法创建数独初盘，将数独问题转化为 SAT 问 题，利用 DPLL 算法对数独进行求解。 3
    2 系统需求分析与总体设计 2.1 系统需求分析 1）输出输入功能：程序参数的输入，cnf 文件的读取，执行结果输出文件保 存。 2）公式解析与验证：读取 cnf 文件，解析文件，并将文件中的数据存入一 定的物理结构。遍历每个子句人工比对是否完全正确。 3）DPLL 算法：基于 DPLL 算法框架，实现 SAT 算例的求解。 4）时间性能的测量：基于相应的处理函数测量出 DPLL 过程所耗费的时间， 并作为输出信息的一部分。 5）程序优化：基于某个方面对程序进行优化，进一步提高程序计算效率 6）SAT 应用：将数独游戏转化成 SAT 问题，并集成到 DPLL 算法框架中进 行求解。 2.2 系统总体设计 2.2.1 系统总流程 用户进入开始界面，若输入 1 则进入数独模块，系统自动随机生成一个数独， 并通过挖洞法生成一个数独初盘，再将数独问题转化为 SAT 问题输出成为一个 cnf 文件，利用 DPLL 算法解出数独问题，最后输出最终的解，输出解出的数独 终盘。若用户输入 2，则进入 SAT 问题求解器模块，系统读入 cnf 文件并将其转 换为定义好的存储结构中，利用 DPLL 算法将问题求解出来，将该结果输出到文 件中。若该问题有解，则输出 1，并输出每个变元的真假值和运行时间；若没有 解，则输出-1，不输出变元的真假值，仅输出运行时间。系统总流程图如下： 4
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料