logo资料库

一类SIR传染病模型的稳定性分析.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.33M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 一类 SIR 传染病模型的稳定性分析 # 吴长青，朱长荣** （重庆大学数学与统计学院，重庆 401331） 5 10 摘要：本篇以非线性发生率为条件，选择在总人口不为常数情况下，研究了一类 SIRS 传染 病模型的解的有界性和平衡点稳定性，包括无病平衡点的稳定性和地方病平衡点的局部稳定 性。运用微分动力系统理论知识证明了无病平衡点是稳定结点，鞍点和退化平衡点。并且使 用 MATLAB 给出了系统在两个平衡点的主要相图，从而进一步验证了本篇理论的正确性。 关键词：传染病模型；局部稳定性；退化平衡点；MATLAB 中图分类号：O193 Stability of A Class of SIRS Epidemic Model Wu Changqing, Zhu Changrong 15 (School of Mathematics and Statistics, Chong Qing University, Chong qing 401331) Abstract: In this paper the dynamics of an SIRS epidemic model are studied. Under the nonlinear incidence condition and without the assumption that the total population is constant, the local stability and boundedness are considered. It has researched the local asymptotic stability at the disease-free equilibrium as well as at the endemic equilibrium. By Dynamic System theory, the disease-free equilibrium can be stable node, saddle, degenerate equilibrium. Finally by using the mathematical software MATLAB, the correctness of the theory is verified. Key words: epidemic model; local stability; degenerate equilibrium; MATLAB 20 25 0 引言 传染病模型是微分动力系统的一个重要组成部分，也是数学与生物学交叉结合的产物之 一。所以数学模型在研究控制传染病的传播过程中已成为一个非常重要的数学工具。从经典 的 Kermack-Mckendrick[1]传染病模型开始，引入了简单的发生率 。1978 年 Capasso 和 Serio [2]研究了以 为发生率的传染病模型。后来许多的研究者，比如 Liu[3] 30 等人研究了更一般的发生率 ，其中有作者也研究了以 [4]为发生率的 SIRS 模型。但是，对于这些绝大部分模型来说，它们都是在总人口规模为常数的假设前提 下，即 ，其中 是常数，去研究模型的理论性态。而在实际生活中却又很难 满足总人口规模不变的假设，因为对于某些疾病来说它的影响时间是比较长的。比如“黑死 病”在欧洲存在了近三百年，它的存在时间尺度是大于人的生存死亡尺度的，这时如果依然 35 采用固定人口规模的模型就显得有些不切实际。所以这里在去掉这一假设前提下的研究工作 就显得尤其的重要。另一方面，针对模型系统本身来讲，是否会因为降阶后的处理而影响或 改变系统本身的性态呢？对这一问题在本篇论文当中也可以得到解决。 为此，本篇论文基于参考文献[4]中以 为发生率的传染病模型 基金项目：国家自然科学基金(11671058) 作者简介：吴长青（1992-），男，硕士研究生，主要研究方向：微分方程与动力系统 通信联系人：朱长荣(1973-)，男，教授、博导，主要研究方向：微分方程与动力系统. E-mail: zhuchangrong126@126.com - 1 - kSI)1/()(IkIIg)1/(qPIkSINRISN21IkSI21IkSI
    中国科技论文在线 http://www.paper.edu.cn 40 45 进行了详细的讨论。其中 和 分别表示 时刻的易感者，感染者和移除者。b 表示人口的出生率，d 表示自然死亡率，k 是一个比例系数， 表示感染者的自然恢复率， 表示移除者失去免疫力再次成为易感者的占有比率， 是一个与接触率有关的参数。 在原论文中，作者主要在平面 ，其中 N 是常数的基础上去研究了系统的 稳定性态，即把原三维系统降阶到二维上去处理，得到了一些很好的结论。本篇作者与之不 同之处在于省去这一假设前提下，从模型本身的角度去研究模型到底存在哪些固有的性态， 这也是本篇论文的一个创新之处。 1 传染病模型 考虑以下模型 （1.1） 50 为了求出系统（1.1）的平衡点，我们可以列出以下方程 （1.2） 从以上方程中我们可以看到，对任意参数，系统都存在无病平衡点 。同时当 时，还存在正平衡点，联立以上三个方程可得到 55 从而可得到该系统的基本再生数 。 （1.3） 。 （1.4） 结合方程（1.3）和（1.4）不难看出，当 时，系统（1.1）只存在无病平衡点。而 当 ， 系 统 （ 1.1 ） 除 了 无 病 平 衡 点 外 ， 还 存 在 正 平 衡 点 ， 即 地 方 病 平 衡 点 。由方程（1.2）可以求出 - 2 - ,)(,)(1,1'2'2'RdIRIdIkSIIRIkSIdSbS)(),(tItS)(tRtNRIS,)(,)(1,1'2'2'RdIRIdIkSIIRIkSIdSbS,0)(,0)(1,0122RdIIdIkSIRIkSIdSb)0,0,(0dbE0I0)()()(2kbddIddkIdd)(0ddkbR10R10R),,(****RISE
    中国科技论文在线 http://www.paper.edu.cn 60 其中 。 以上是对系统（1.1）的平衡点的一个归纳。下面将对这两个平衡点的稳定性进行讨论。 2 解的有界性和平衡点的稳定性 2.1 解的有界性 65 定理 2.1 系统（1.1）中的所有解曲线都有界。 证明：下面将分两种情况对该定理进行证明，将方程（1.2）中三个方程相加可得 。 （2.1） （1）如果初值 ，则对方程（ 2.1）存在时间 ，使得当 时有 ，即 是关于时间 的单调递减函数，所以有 。 70 （2）如果初值 ，同样对方程（2.1）存在时间 ，使得当 时有 ，即 是关于时间 的单调递增函数，所以有 。一旦 ， 就又是情形（1）中的情况了。 2.2 平衡点的稳定性 本篇论文考虑的系统平衡点稳定性不单是在平面 上，而是在整个空间 75 中的第一卦象内去讨论。这里也不会对系统（1.1）进行平移变换，而将从模型本身出发去 研究系统在平衡点处的稳定性。 系统（1.1）在平衡点的线性化系统的线性化矩阵为 。 其对应在无病平衡点 的线性化矩阵为 - 3 - ,,)(2))((4,**222***IdRddkbddddmkkmIdmIbSdddm)(dNbdtdNdbtN)(01T),(10Ttt0dtdN)(tNt)()(0tNtNdbtN)(02T),(20Ttt0dtdN)(tNt)()(0tNtN)()(0tNtNdbRIS3R)(00)()1()1(1)1()1(122222222ddIIkSIkIIIkSIkIdM)0,0,(0dbE
    中国科技论文在线 http://www.paper.edu.cn 80 ， 可以看出，如果 ，矩阵 有三个负特征根，由微分方程定性理论[5]知道，此时无病 平衡点是稳定的结点。如果 ，则有 ，所以此时的无病平衡点是不稳定的。 由分岔理论知识我们知道，系统在 处将发生鞍-结分岔。 设 ，由定理 2.1 解的有界性知道，对系统（1.1）中的任意解 ， 85 都有 ，这种情况下，由 Dulac[4]函数知道，此时平衡点 是全局渐进稳定的。总 结以上知识，于是得出下面的定理 定理 2.2 系统（1.1）在无病平衡点 的稳定性存在以下三种可能 （1）如果 ，则 是系统的稳定结点； （2）如果 ，则 是系统的鞍点； 90 （3）如果 ，则 是系统的鞍-结点。 下面将讨论当 时，地方病平衡点 的局部稳定性。当 时， 由方程（1.2）中的第二个方程可得到 。系统（1.1）在地方病平衡点 处 的线性化矩阵为 95 。 （2.2） 不难看出 。所以矩阵 的特征根符号有两种情况， 或者 的形 式。也就是说平衡点 要么是稳定的结点，要么是不稳定的鞍点。为此还需要做进一步判 断，这个可以用 Routh-Hurwitz[6]判定准则进行推理论证，下面给出判定平衡点 的稳定性 定理。 - 4 - )(00)(00dddkbdkbdM10R0M10R1det0M10R}),(max{0dbtNA)(tNAtN)(0E)0,0,(0dbE10R0E10R0E10R0E10R),,(****RISE0IdIkS2*1*E)(00)(1)1)((11)1)((12*2*2**2*2*2**1ddIIdIkIIIdIkIdM，)]()(2[1-1))(()1)]()(([)det(*22**2*2*2**1dkIdddIIIIdddddIkIddM0)det(1M1M),,(),,(*E*E
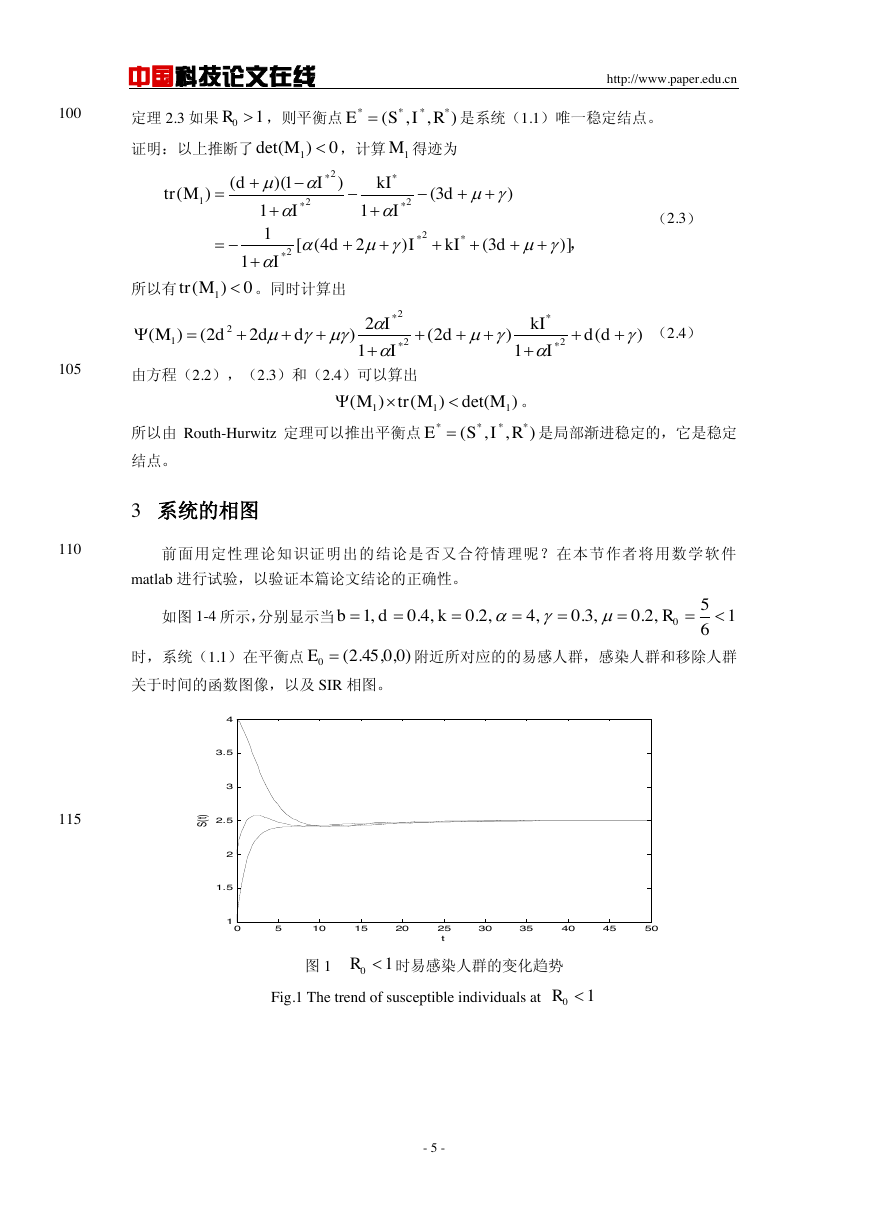
    中国科技论文在线 http://www.paper.edu.cn 100 定理 2.3 如果 ，则平衡点 是系统（1.1）唯一稳定结点。 证明：以上推断了 ，计算 得迹为 所以有 。同时计算出 （2.3） （2.4） 105 由方程（2.2），（2.3）和（2.4）可以算出 。 所以由 Routh-Hurwitz 定理可以推出平衡点 是局部渐进稳定的，它是稳定 结点。 3 系统的相图 110 前面用定性理论知识证明出的结论是否又合符情理呢？在本节作者将用数学软件 matlab 进行试验，以验证本篇论文结论的正确性。 如图 1-4 所示，分别显示当 时，系统（1.1）在平衡点 附近所对应的的易感人群，感染人群和移除人群 关于时间的函数图像，以及 SIR 相图。 115 图 1 时易感染人群的变化趋势 Fig.1 The trend of susceptible individuals at - 5 - 10R),,(****RISE0)det(1M1M，)]3()24([11)3(11)1)(()(*2*2*2**2*2*1dkIIdIdIkIIIdMtr0)(1Mtr)(1)2(12)22()(2**2*2*21ddIkIdIIdddM)det()()(111MMtrM),,(****RISE165,2.0,3.0,4,2.0,4.0,10Rkdb)0,0,45.2(0E10R10R0510152025303540455011.522.533.54tS(t)
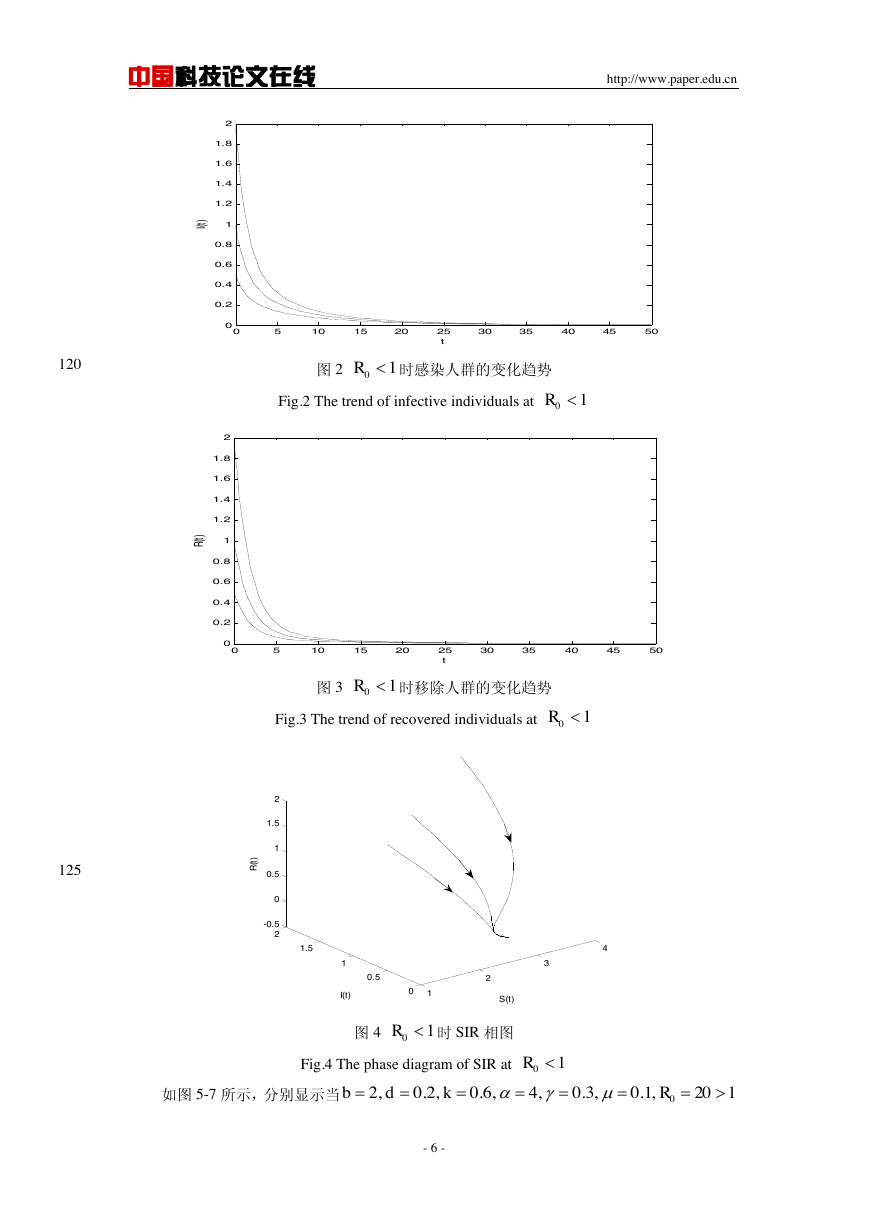
    中国科技论文在线 http://www.paper.edu.cn 120 图 2 时感染人群的变化趋势 Fig.2 The trend of infective individuals at 图 3 时移除人群的变化趋势 Fig.3 The trend of recovered individuals at 125 图 4 时 SIR 相图 Fig.4 The phase diagram of SIR at 如图 5-7 所示，分别显示当 - 6 - 10R10R10R10R10R10R120,1.0,3.0,4,6.0,2.0,20Rkdb0510152025303540455000.20.40.60.811.21.41.61.82tI(t)0510152025303540455000.20.40.60.811.21.41.61.82tR(t)123400.511.52-0.500.511.52S(t)I(t)R(t)
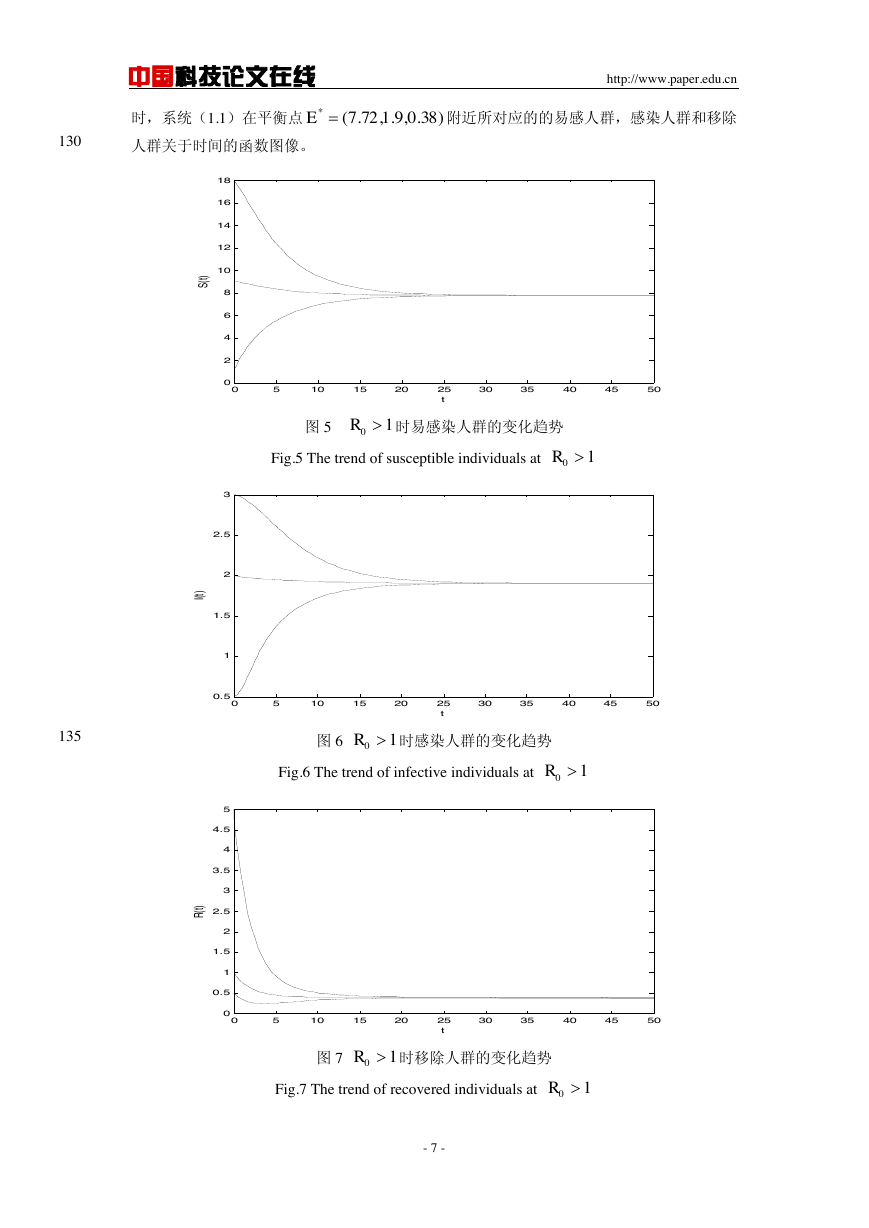
    中国科技论文在线 http://www.paper.edu.cn 时，系统（1.1）在平衡点 附近所对应的的易感人群，感染人群和移除 130 人群关于时间的函数图像。 图 5 时易感染人群的变化趋势 Fig.5 The trend of susceptible individuals at 135 图 6 时感染人群的变化趋势 Fig.6 The trend of infective individuals at 图 7 时移除人群的变化趋势 Fig.7 The trend of recovered individuals at - 7 - )38.0,9.1,72.7(*E10R10R10R10R10R10R05101520253035404550024681012141618tS(t)051015202530354045500.511.522.53tI(t)0510152025303540455000.511.522.533.544.55tR(t)
    中国科技论文在线 http://www.paper.edu.cn 140 4 结论 总结定理 2.1-2.3，对系统（1.1）的稳定性结论，本文给出了以下结论 定理 2.4 关于系统（1.1）的稳定性存在以下三个结论 （1）如果基本再生数 ，则系统（1.1）只存在无病平衡点 ，并且是 全局渐进稳定的。 145 （2）如果基本再生数 ，则系统（1.1）存在无病平衡点 和地方病平 衡点 ；并且 是局部渐进稳定的。 （3）如果基本再生数 ，则系统（1.1）只存在无病平衡点 ，此时该 点是一个极不稳定的鞍-结点。 150 [参考文献] (References) [1] KERMACK W O, MCKENDRICK A G. A contribution to the mathematical theory of epidemics[J]. Proc Roy Soc, 1927, Ser A(115): 700-721. [2] BRAUER F, CARLOS C C. Mathematical models in population biology and epidemiology[M]. Springer, 2012. [3] LIU W M, HETHCOTE H W, LEVIN S A. Dynamical behavior of epidemiological models with nonlinear incidence rates[J], J Math Biol, 1987, (25): 359-380. [4] XIAO D M, RUAN S G. Global analysis of an epidemic model with nonmonotone incidence rate[J]. Math Biol, 2007, (208): 419-429. [5] 张锦炎, 冯贝叶. 常微分方程几何理论与分支问题[M]. 北京：北京大学出版社，2009. [6] ZHU H, CAMPBELL S A, WOLKOWICZ G S K. Bifurcation analysis of a predator-prey system with nonmonotonic functional response[J]. J Appl Math, 2002, (63): 636-682. 155 160 - 8 - 10R)0,0,(0dbE10R)0,0,(0dbE),,(****RISE*E10R)0,0,(0dbE
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料